Topic what is the square root of - 36: Ever wondered what the square root of -36 is? Dive into the intriguing realm of complex numbers and uncover how the concept of imaginary units transforms our understanding of negative square roots. This article will guide you through the calculation and significance of the square root of -36, making complex mathematics both accessible and exciting.
Table of Content
- Understanding the Square Root of -36
- Introduction to Square Roots and Complex Numbers
- Understanding Negative Numbers and Square Roots
- The Concept of Imaginary Numbers
- Step-by-Step Calculation Process
- Mathematical Definition and Properties
- Applications of Complex Numbers
- Visualizing Complex Numbers
- Frequently Asked Questions about Square Roots of Negative Numbers
- Summary and Key Takeaways
- YOUTUBE: Video này cung cấp hướng dẫn toàn diện về căn bậc hai của -36 và giới thiệu số phức.
Understanding the Square Root of -36
The concept of the square root of a negative number often introduces the idea of complex numbers in mathematics. Here's a detailed explanation:
Definition
The square root of a number \( x \) is a value \( y \) such that \( y^2 = x \). For negative numbers, this definition extends into the realm of complex numbers.
Complex Numbers
A complex number is a number that can be expressed in the form \( a + bi \), where \( a \) and \( b \) are real numbers, and \( i \) is the imaginary unit, which satisfies the equation \( i^2 = -1 \).
Calculating the Square Root of -36
- Identify the positive counterpart: The positive counterpart of -36 is 36.
- Find the square root of 36: \( \sqrt{36} = 6 \).
- Apply the imaginary unit: Since \( i^2 = -1 \), the square root of -36 is \( 6i \).
Conclusion
Therefore, the square root of -36 is \( 6i \). This result leverages the concept of imaginary numbers, which are an essential part of complex number theory.
Summary Table
| Expression | Result |
| \( \sqrt{-36} \) | 6i |
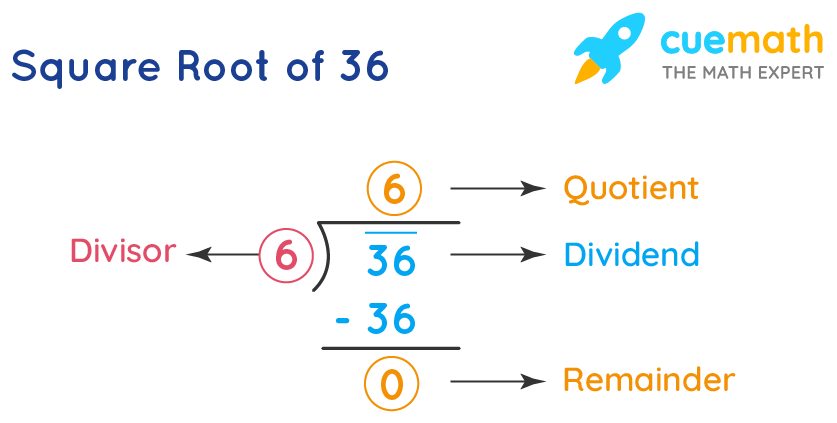
READ MORE:
Introduction to Square Roots and Complex Numbers
The square root of a number is a value that, when multiplied by itself, gives the original number. For positive numbers, this concept is straightforward. However, when dealing with negative numbers, the concept extends to complex numbers.
Complex numbers consist of a real part and an imaginary part and are written in the form \( a + bi \), where \( a \) and \( b \) are real numbers, and \( i \) is the imaginary unit, defined by the property \( i^2 = -1 \).
To understand the square root of -36, we need to follow these steps:
- Identify the positive counterpart: The positive counterpart of -36 is 36.
- Calculate the square root of the positive number: \( \sqrt{36} = 6 \).
- Incorporate the imaginary unit: Since \( i^2 = -1 \), the square root of -36 is represented as \( 6i \).
Complex numbers are essential in various fields, including engineering, physics, and applied mathematics, because they allow for the solution of equations that do not have real-number solutions.
Here's a summary in tabular form:
| Expression | Result |
| \( \sqrt{36} \) | 6 |
| \( \sqrt{-36} \) | 6i |
This introduction provides a foundation for understanding how square roots of negative numbers lead to complex numbers, expanding the boundaries of traditional mathematics.
Understanding Negative Numbers and Square Roots
Negative numbers present unique challenges in mathematics, especially when dealing with square roots. The square root of a number \( x \) is a value \( y \) such that \( y^2 = x \). For positive numbers, this is straightforward, but for negative numbers, it requires a deeper exploration into complex numbers.
Here's how to approach the square root of a negative number, such as -36:
- Recognize the issue: The square root of a negative number is not a real number because no real number squared equals a negative number.
- Introduce the imaginary unit \( i \): The imaginary unit \( i \) is defined by the property \( i^2 = -1 \). This allows us to express the square root of negative numbers.
- Reframe the problem: To find \( \sqrt{-36} \), consider it as \( \sqrt{36 \cdot -1} \).
- Separate the terms: This can be split into \( \sqrt{36} \cdot \sqrt{-1} \).
- Simplify: We know that \( \sqrt{36} = 6 \) and \( \sqrt{-1} = i \), so \( \sqrt{-36} = 6i \).
This process shows that the square root of a negative number involves both a real number and the imaginary unit \( i \). Complex numbers, therefore, are a combination of real and imaginary parts, written as \( a + bi \), where \( a \) is the real part and \( b \) is the imaginary part.
Below is a summary table:
| Expression | Result |
| \( \sqrt{36} \) | 6 |
| \( \sqrt{-1} \) | i |
| \( \sqrt{-36} \) | 6i |
Understanding the square root of negative numbers through the lens of complex numbers not only solves mathematical problems but also expands our comprehension of number systems beyond the real numbers.
The Concept of Imaginary Numbers
Imaginary numbers are a fundamental part of complex numbers, which extend our understanding of traditional number systems. The imaginary unit, denoted as \( i \), is defined by the property that \( i^2 = -1 \). This definition allows us to handle the square roots of negative numbers, which are not possible within the realm of real numbers.
To comprehend imaginary numbers, follow these steps:
- Understanding the Basics: Real numbers are inadequate for solving equations like \( x^2 + 1 = 0 \) because no real number squared equals -1.
- Introducing the Imaginary Unit: The imaginary unit \( i \) is introduced, where \( i \) satisfies \( i^2 = -1 \). This enables us to redefine the square roots of negative numbers.
- Formulating Complex Numbers: A complex number is composed of a real part and an imaginary part, written as \( a + bi \), where \( a \) and \( b \) are real numbers. For example, \( 3 + 4i \) is a complex number.
- Calculating with Imaginary Numbers: Consider the square root of -36. We can express this as \( \sqrt{-36} = \sqrt{36 \cdot -1} = \sqrt{36} \cdot \sqrt{-1} = 6i \).
Imaginary numbers play a critical role in various fields, including engineering, physics, and applied mathematics. They enable us to solve equations and perform calculations that would otherwise be impossible with only real numbers.
Here's a summary table to illustrate the concept:
| Expression | Result |
| \( i \) | \( \sqrt{-1} \) |
| \( i^2 \) | -1 |
| \( \sqrt{-36} \) | 6i |
By understanding imaginary numbers, we expand our mathematical toolkit, allowing us to address problems and equations that extend beyond the scope of real numbers.
Step-by-Step Calculation Process
Calculating the square root of a negative number, such as -36, requires an understanding of both real and imaginary numbers. Here is a detailed, step-by-step process:
- Recognize the Problem: The square root of -36 involves a negative number under the square root, which means we need to use imaginary numbers.
- Express the Negative Number: Rewrite -36 as a product of 36 and -1: \( -36 = 36 \cdot (-1) \).
- Separate the Terms: Use the property of square roots to separate the product into two square roots: \[ \sqrt{-36} = \sqrt{36 \cdot -1} = \sqrt{36} \cdot \sqrt{-1} \]
- Calculate the Square Root of 36: Determine the square root of the positive number 36: \[ \sqrt{36} = 6 \] because \( 6 \times 6 = 36 \).
- Introduce the Imaginary Unit: Understand that the square root of -1 is the imaginary unit \( i \), where \[ i^2 = -1 \] Thus, \[ \sqrt{-1} = i \].
- Combine the Results: Multiply the results of the two square roots: \[ \sqrt{36} \cdot \sqrt{-1} = 6 \cdot i = 6i \].
Therefore, the square root of -36 is \( 6i \), where \( i \) represents the imaginary unit. This step-by-step process shows how to handle negative square roots using complex numbers.
Here is a summary in tabular form:
| Expression | Result |
| \( \sqrt{36} \) | 6 |
| \( \sqrt{-1} \) | i |
| \( \sqrt{-36} \) | 6i |
By following this method, you can accurately calculate the square roots of negative numbers and understand the role of imaginary numbers in these calculations.
Mathematical Definition and Properties
The square root of a number is defined as a value that, when multiplied by itself, gives the original number. For real numbers, this is straightforward, but for negative numbers, the concept requires the introduction of imaginary numbers.
Here is the step-by-step mathematical definition and properties of the square root of -36:
- Definition of Square Root: The square root of a number \( x \) is a value \( y \) such that \( y^2 = x \). For example, the square root of 36 is 6 because \( 6^2 = 36 \).
- Negative Numbers and Imaginary Unit: For negative numbers, the square root involves the imaginary unit \( i \), where \( i \) is defined by \( i^2 = -1 \).
- Expressing Negative Numbers: To find the square root of -36, rewrite it as: \[ \sqrt{-36} = \sqrt{36 \cdot (-1)} \].
- Separating the Terms: Use the property of square roots to separate the product into two square roots: \[ \sqrt{-36} = \sqrt{36} \cdot \sqrt{-1} \].
- Calculating the Square Roots: Determine the square root of each term: \[ \sqrt{36} = 6 \] and \[ \sqrt{-1} = i \].
- Combining the Results: Multiply the results: \[ \sqrt{-36} = 6 \cdot i = 6i \].
In summary, the square root of -36 is \( 6i \). This is a complex number, composed of a real part and an imaginary part.
Properties of the square root involving imaginary numbers include:
- \( i^2 = -1 \)
- Imaginary numbers are represented as \( bi \), where \( b \) is a real number.
- Complex numbers are in the form \( a + bi \), where \( a \) and \( b \) are real numbers.
Here is a summary in tabular form:
| Expression | Result |
| \( \sqrt{36} \) | 6 |
| \( \sqrt{-1} \) | i |
| \( \sqrt{-36} \) | 6i |
By understanding these definitions and properties, we can accurately work with the square roots of negative numbers and comprehend their applications in various fields of mathematics and science.
Applications of Complex Numbers
Complex numbers, including those with imaginary parts, have a wide range of applications in various fields of science and engineering. Below are some of the key applications:
1. Electrical Engineering
Complex numbers are extensively used in electrical engineering, especially in the analysis of AC circuits. They help in representing and solving problems involving sinusoidal voltages and currents.
- AC Circuit Analysis: Complex numbers simplify the analysis of AC circuits by using phasor representation of voltages and currents.
- Impedance Calculations: The impedance of circuit elements (resistors, capacitors, and inductors) can be represented as complex numbers, facilitating easier calculations.
2. Control Systems
Control systems engineering makes use of complex numbers to analyze and design control systems.
- Stability Analysis: Complex numbers are used in the root locus method and Bode plots to determine system stability.
- Transfer Functions: Transfer functions, which describe the input-output relationship of systems, often involve complex numbers.
3. Signal Processing
In signal processing, complex numbers play a crucial role in the analysis and processing of signals.
- Fourier Transform: The Fourier transform, which decomposes signals into their frequency components, involves complex numbers.
- Filter Design: Complex numbers are used in the design of digital and analog filters to process signals.
4. Quantum Physics
Complex numbers are fundamental in quantum physics, where they are used to describe the state of quantum systems.
- Wave Functions: The wave function, which describes the probability amplitude of a quantum system, is a complex-valued function.
- Schrödinger Equation: The Schrödinger equation, which governs the behavior of quantum systems, involves complex numbers.
5. Fluid Dynamics
In fluid dynamics, complex numbers are used to solve problems related to fluid flow.
- Potential Flow: Complex potential functions simplify the analysis of two-dimensional, incompressible fluid flow.
- Conformal Mapping: Complex analysis techniques, such as conformal mapping, are used to solve complex flow problems.
6. Mechanical Vibrations
Complex numbers are employed in the study of mechanical vibrations to analyze oscillatory systems.
- Harmonic Oscillators: The behavior of harmonic oscillators, which are systems that exhibit periodic motion, is described using complex numbers.
- Resonance Analysis: Complex numbers help in analyzing resonance conditions in mechanical systems.
7. Digital Communications
In digital communications, complex numbers are used to represent and process signals.
- Modulation Techniques: Techniques such as QAM (Quadrature Amplitude Modulation) use complex numbers to modulate and demodulate signals.
- Signal Representation: Complex numbers represent the amplitude and phase of signals in communication systems.
Overall, complex numbers are a powerful mathematical tool with diverse applications in various fields, enabling the analysis and solution of many complex problems.
Visualizing Complex Numbers
Complex numbers can be visualized in a two-dimensional plane known as the complex plane or Argand plane. This visualization helps in understanding their properties and operations. Here’s how to visualize and interpret complex numbers step-by-step:
1. The Complex Plane
The complex plane consists of two axes:
- Real Axis: The horizontal axis represents the real part of complex numbers.
- Imaginary Axis: The vertical axis represents the imaginary part of complex numbers.
A complex number \( z = a + bi \) is plotted as a point in this plane where \( a \) is the real part and \( b \) is the imaginary part.
2. Plotting Complex Numbers
To plot a complex number, follow these steps:
- Locate the real part \( a \) on the horizontal axis.
- Locate the imaginary part \( b \) on the vertical axis.
- Plot the point \((a, b)\) in the complex plane.
For example, to plot \( 3 + 4i \), move 3 units along the real axis and 4 units along the imaginary axis.
3. Representing Complex Numbers
Complex numbers can also be represented in polar form as \( z = r(\cos \theta + i \sin \theta) \) or \( z = re^{i\theta} \), where:
- \( r \) is the magnitude (or modulus) of the complex number, calculated as \( r = \sqrt{a^2 + b^2} \).
- \( \theta \) is the argument (or angle), calculated as \( \theta = \tan^{-1}\left(\frac{b}{a}\right) \).
4. Examples and Visualization
Let's visualize some examples:
- Example 1: For the complex number \( 1 + i \):
- Real part \( a = 1 \)
- Imaginary part \( b = 1 \)
- Magnitude \( r = \sqrt{1^2 + 1^2} = \sqrt{2} \)
- Argument \( \theta = \tan^{-1}(1/1) = \pi/4 \)
This can be represented as a point (1, 1) in the complex plane or in polar form as \( \sqrt{2}e^{i\pi/4} \).
- Example 2: For the complex number \( -2 + 2i \):
- Real part \( a = -2 \)
- Imaginary part \( b = 2 \)
- Magnitude \( r = \sqrt{(-2)^2 + 2^2} = 2\sqrt{2} \)
- Argument \( \theta = \tan^{-1}(2/-2) = -\pi/4 \)
This can be represented as a point (-2, 2) in the complex plane or in polar form as \( 2\sqrt{2}e^{-i\pi/4} \).
5. Operations in the Complex Plane
Operations like addition, subtraction, multiplication, and division of complex numbers can be visualized as transformations in the complex plane:
- Addition: Adding two complex numbers corresponds to vector addition in the complex plane.
- Subtraction: Subtracting two complex numbers corresponds to vector subtraction in the complex plane.
- Multiplication: Multiplying complex numbers involves rotating and scaling vectors in the complex plane.
- Division: Dividing complex numbers involves reversing the rotation and scaling of vectors in the complex plane.
By visualizing complex numbers in the complex plane, we gain a deeper understanding of their properties and operations.
Frequently Asked Questions about Square Roots of Negative Numbers
What is the square root of -36?
The square root of -36 is a complex number. Specifically, it is represented as:
\[ \sqrt{-36} = \sqrt{36} \cdot \sqrt{-1} = 6i \]
Here, \( i \) is the imaginary unit, which is defined as \( i = \sqrt{-1} \).
Why can't we take the square root of a negative number in the real number system?
In the real number system, the square of any real number is always non-negative. Therefore, there is no real number whose square is negative. This limitation leads to the introduction of imaginary numbers to extend the number system and handle square roots of negative numbers.
What is an imaginary number?
An imaginary number is a number that can be written as a real number multiplied by the imaginary unit \( i \), where \( i \) is defined as \( i^2 = -1 \). For example, \( 3i \) and \( -5i \) are imaginary numbers.
What are complex numbers?
Complex numbers are numbers that have both a real part and an imaginary part. They are written in the form \( a + bi \), where \( a \) is the real part and \( b \) is the imaginary part. For example, \( 2 + 3i \) and \( -1 - 4i \) are complex numbers.
How do we calculate the square root of a negative number?
To calculate the square root of a negative number, follow these steps:
- Factor the negative number into a positive number and -1.
- Take the square root of the positive number.
- Multiply the result by \( i \), the imaginary unit.
For example, to find the square root of -49:
- Factor -49 as \( 49 \cdot -1 \).
- The square root of 49 is 7.
- Multiply 7 by \( i \) to get \( 7i \).
- Therefore, \( \sqrt{-49} = 7i \).
Are there practical applications of square roots of negative numbers?
Yes, square roots of negative numbers and complex numbers have practical applications in various fields:
- Electrical Engineering: Complex numbers are used to analyze AC circuits and signal processing.
- Control Systems: Complex numbers help in the stability analysis and design of control systems.
- Quantum Physics: Complex numbers are fundamental in describing the state of quantum systems.
- Fluid Dynamics: Complex analysis techniques are used to solve problems related to fluid flow.
What are some common misconceptions about imaginary numbers?
Some common misconceptions include:
- Imaginary numbers are "imaginary" and not real or useful. In reality, they are essential in various scientific and engineering disciplines.
- Imaginary numbers are difficult to understand. With practice and visualization techniques, such as the complex plane, they become more intuitive.
Understanding the square roots of negative numbers and the concept of imaginary and complex numbers opens up a new realm of mathematical and practical applications.
Summary and Key Takeaways
In this guide, we have explored the concept of the square root of negative numbers and delved into the world of complex numbers. Below are the key takeaways:
- Definition of Imaginary Unit: The imaginary unit \( i \) is defined as \( i = \sqrt{-1} \), and \( i^2 = -1 \). This fundamental concept allows us to extend the real number system to include complex numbers.
- Square Root of -36: The square root of -36 is calculated as:
\[ \sqrt{-36} = \sqrt{36} \cdot \sqrt{-1} = 6i \]
Thus, \( \sqrt{-36} = 6i \).
- Imaginary and Complex Numbers: Imaginary numbers are real numbers multiplied by \( i \), and complex numbers have both a real part and an imaginary part, expressed as \( a + bi \).
- Complex Plane: Complex numbers can be visualized in the complex plane (Argand plane), where the horizontal axis represents the real part and the vertical axis represents the imaginary part. This visualization aids in understanding their properties and operations.
- Applications of Complex Numbers: Complex numbers have numerous applications in fields such as electrical engineering, control systems, signal processing, quantum physics, fluid dynamics, mechanical vibrations, and digital communications.
- Calculation Steps for Square Roots of Negative Numbers: To find the square root of a negative number:
- Factor the negative number into a positive number and -1.
- Take the square root of the positive number.
- Multiply the result by \( i \), the imaginary unit.
- Common Misconceptions: Misconceptions include the belief that imaginary numbers are not useful or that they are too difficult to understand. In reality, they are essential and become intuitive with practice.
- Importance of Complex Numbers: Understanding and utilizing complex numbers is crucial for solving a wide range of practical and theoretical problems in mathematics, engineering, and science.
Overall, the study of the square root of negative numbers and complex numbers enriches our mathematical knowledge and provides powerful tools for various applications.
Video này cung cấp hướng dẫn toàn diện về căn bậc hai của -36 và giới thiệu số phức.
Hướng dẫn Toàn diện về Căn Bậc Hai của -36
READ MORE:
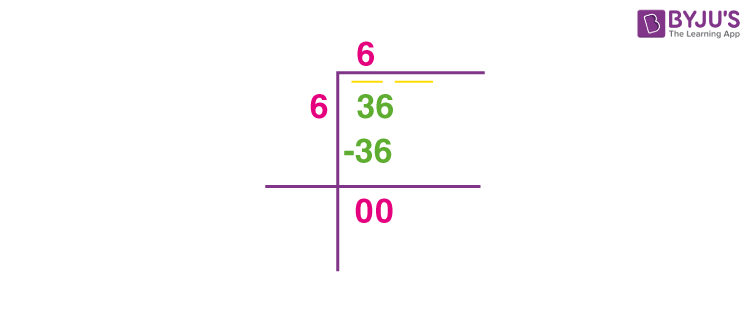
Video hướng dẫn cách tìm căn bậc hai của số 36, với giải thích chi tiết và dễ hiểu, phù hợp cho mọi lứa tuổi.
Tìm Căn Bậc Hai: √36