Topic is the square root of 36 rational or irrational: Ever wondered whether the square root of 36 is rational or irrational? In this article, we delve into the properties of square roots, explore the definitions of rational and irrational numbers, and reveal why the square root of 36 is classified as a rational number. Join us on this mathematical journey!
Table of Content
- Is the Square Root of 36 Rational or Irrational?
- Introduction to Square Roots
- Definition of Rational and Irrational Numbers
- Properties of Perfect Squares
- Why the Square Root of 36 is Rational
- Examples of Rational and Irrational Numbers
- Common Misconceptions About Square Roots
- Applications of Rational Numbers in Real Life
- Conclusion: The Rationality of Square Root of 36
- YOUTUBE: Video giải thích tại sao căn bậc hai của 36 chỉ là 6 dương. Tìm hiểu thêm về lý do và tính hợp lý của kết quả này.
Is the Square Root of 36 Rational or Irrational?
The square root of 36 is a number that, when multiplied by itself, gives 36. To determine if this number is rational or irrational, let's explore its properties.
Understanding Rational and Irrational Numbers
- Rational Numbers: These are numbers that can be expressed as a fraction \(\frac{a}{b}\) where \(a\) and \(b\) are integers and \(b \neq 0\). Examples include \( \frac{1}{2} \), \(3\), and \(-4\).
- Irrational Numbers: These cannot be expressed as a simple fraction. Examples include \(\pi\) and \(\sqrt{2}\).
Calculating the Square Root of 36
The square root of 36 is:
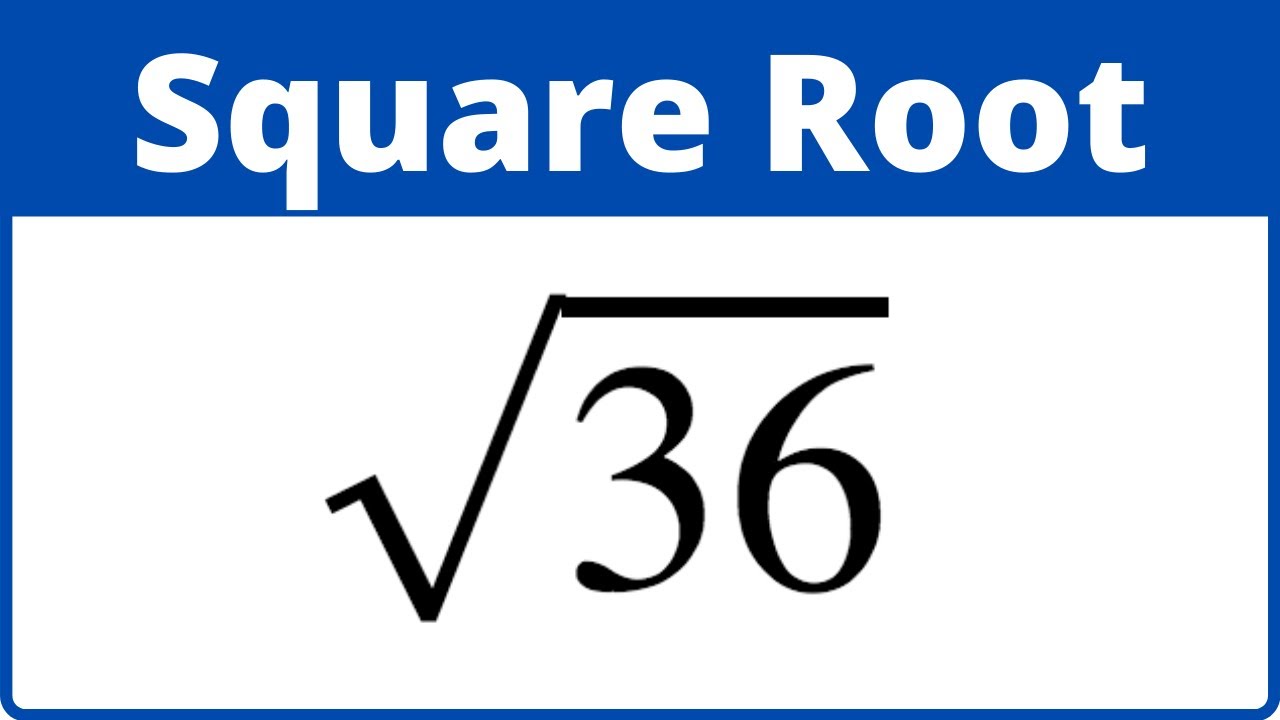
\[\sqrt{36} = 6\]
Conclusion
Since 6 can be expressed as the fraction \(\frac{6}{1}\), it is a rational number. Therefore, the square root of 36 is rational.
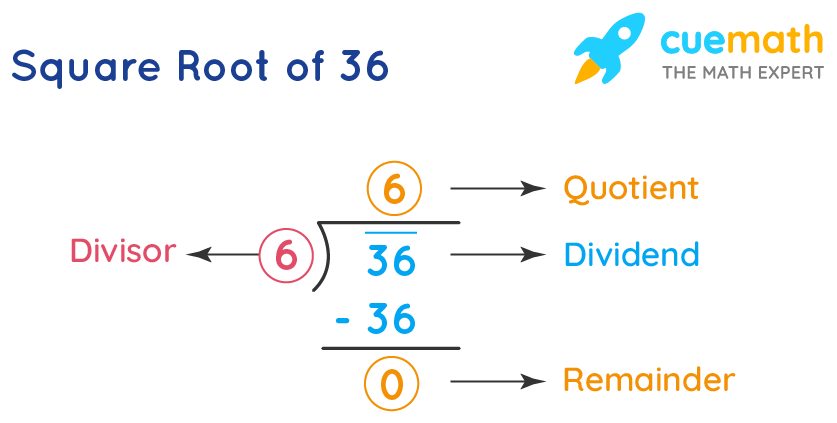
READ MORE:
Introduction to Square Roots
Square roots are fundamental concepts in mathematics, representing a value that, when multiplied by itself, gives the original number. Understanding square roots is crucial for various mathematical applications, including algebra and geometry.
Here is a step-by-step breakdown to understand square roots:
- Definition: The square root of a number \( x \) is a number \( y \) such that \( y^2 = x \). This is often written as \( \sqrt{x} = y \).
- Notation: The square root symbol \( \sqrt{} \) denotes the principal square root, which is always non-negative.
- Perfect Squares: Numbers like 1, 4, 9, 16, 25, and 36 are perfect squares because their square roots are whole numbers. For example, \( \sqrt{36} = 6 \).
- Rational vs. Irrational: A square root is rational if it can be expressed as a fraction \( \frac{a}{b} \) where \( a \) and \( b \) are integers. If not, it is irrational.
In the case of 36, it is a perfect square, making its square root a rational number. Understanding these basics allows us to explore deeper mathematical concepts and their applications in solving real-world problems.
Definition of Rational and Irrational Numbers
Understanding the difference between rational and irrational numbers is key to grasping various mathematical concepts. Let's explore these definitions in detail:
- Rational Numbers:
- A rational number is any number that can be expressed as a fraction \(\frac{a}{b}\), where \(a\) and \(b\) are integers, and \(b \neq 0\).
- Examples of rational numbers include \( \frac{1}{2} \), \(3\), \( \frac{-4}{5} \), and \(0\).
- Decimal representations of rational numbers either terminate (e.g., \(0.75\)) or repeat periodically (e.g., \(0.333...\)).
- Irrational Numbers:
- An irrational number cannot be expressed as a simple fraction \(\frac{a}{b}\).
- Examples of irrational numbers include \( \pi \), \( \sqrt{2} \), and the Euler's number \( e \).
- Decimal representations of irrational numbers are non-terminating and non-repeating.
To summarize, rational numbers can be neatly expressed as fractions, while irrational numbers cannot. This distinction is crucial when working with different types of numbers in mathematics.
Properties of Perfect Squares
Perfect squares are numbers that are the square of an integer. These numbers have unique properties that make them fundamental in mathematics. Let's explore these properties step by step:
- Definition:
- A perfect square is a number that can be expressed as \( n^2 \), where \( n \) is an integer. For example, \( 1, 4, 9, 16, 25, \) and \( 36 \) are perfect squares.
- Integer Square Roots:
- The square root of a perfect square is always an integer. For instance, \( \sqrt{36} = 6 \).
- Sum of Consecutive Odd Numbers:
- A perfect square can be expressed as the sum of the first \( n \) odd numbers. For example, \( 36 = 1 + 3 + 5 + 7 + 9 + 11 \).
- Geometric Representation:
- Perfect squares can be represented as a square with integer side lengths. For example, a square with side length 6 has an area of \( 6^2 = 36 \).
- Factors:
- Perfect squares have an odd number of total factors. For example, 36 has the factors \( 1, 2, 3, 4, 6, 9, 12, 18, 36 \), totaling 9 factors.
- Algebraic Identities:
- Perfect squares often appear in algebraic identities such as \( (a + b)^2 = a^2 + 2ab + b^2 \).
These properties highlight the special nature of perfect squares and their significance in various mathematical contexts. Recognizing and understanding these properties can aid in solving complex mathematical problems more efficiently.
Why the Square Root of 36 is Rational
To understand why the square root of 36 is rational, we need to delve into the definitions and properties of rational numbers and square roots. Here’s a detailed explanation:
- Definition of Rational Numbers:
- A rational number is any number that can be expressed as a fraction \(\frac{a}{b}\), where \(a\) and \(b\) are integers and \(b \neq 0\).
- Square Roots of Perfect Squares:
- Perfect squares are numbers that can be expressed as the square of an integer. For example, 36 is a perfect square because it can be written as \(6^2\).
- The square root of a perfect square is always an integer. Thus, \(\sqrt{36} = 6\).
- Expressing the Square Root as a Fraction:
- Since 6 is an integer, it can be expressed as a fraction \(\frac{6}{1}\), which fits the definition of a rational number.
- Verification:
- To further confirm, consider that rational numbers have terminating or repeating decimal expansions. The decimal form of 6 is simply 6.0, which terminates.
- Conclusion:
- Based on these points, we can conclude that the square root of 36 is rational because it is an integer and can be expressed as a fraction. Thus, \(\sqrt{36} = 6\) is a rational number.
Understanding these principles helps clarify why the square root of 36, a perfect square, is indeed a rational number.

Examples of Rational and Irrational Numbers
Understanding the difference between rational and irrational numbers is crucial for various mathematical concepts. Here are some examples to illustrate the distinction:
Rational Numbers
Rational numbers are numbers that can be expressed as the quotient or fraction of two integers, where the denominator is not zero. They can be integers, terminating decimals, or repeating decimals. Here are some examples:
- Integers: -3, 0, 7
- Fractions: 1/2, -4/5, 22/7
- Terminating Decimals: 0.5 (which is 1/2), 3.75 (which is 15/4)
- Repeating Decimals: 0.333... (which is 1/3), 2.142857142857... (which is 3/14)
Irrational Numbers
Irrational numbers cannot be expressed as a simple fraction; their decimal forms are non-terminating and non-repeating. Some famous irrational numbers include:
- Square roots of non-perfect squares: √2, √3, √5
- Mathematical constants: π (pi), e (the base of natural logarithms)
- Non-repeating, non-terminating decimals: 0.101001000100001... (a number with a pattern that does not repeat in a predictable way)
To summarize, the key difference is that rational numbers have a repeating or terminating decimal representation, while irrational numbers do not. Understanding these differences helps in various mathematical applications and problem-solving scenarios.
Common Misconceptions About Square Roots
Square roots can be a source of confusion, leading to several common misconceptions. Here, we address some of the most frequent misunderstandings:
- Misconception 1: All Square Roots are Irrational
Many people believe that all square roots are irrational numbers. While it is true for the square roots of non-perfect squares (e.g., √2 or √3), the square roots of perfect squares are rational numbers. For instance, √36 equals 6, which is a rational number because it can be expressed as the fraction 6/1.
- Misconception 2: The Square Root Symbol Always Yields a Positive Number
The principal square root (denoted by the radical symbol √) is indeed positive, but each positive number actually has two square roots: one positive and one negative. For example, √36 equals 6, but -6 is also a square root of 36 since (-6)² = 36.
- Misconception 3: Square Roots of Negative Numbers Are Real
In the realm of real numbers, the square root of a negative number does not exist. However, in the complex number system, the square root of a negative number is possible and involves the imaginary unit i, where i² = -1. For example, √-36 equals 6i.
- Misconception 4: Only Integers Can Have Rational Square Roots
It is often thought that only integers can have rational square roots. However, any rational number whose numerator and denominator are perfect squares also has a rational square root. For instance, the square root of 1/4 is 1/2.
- Misconception 5: The Square Root of a Sum Equals the Sum of the Square Roots
This is incorrect. The square root of a sum does not equal the sum of the square roots. For example, √(36 + 64) does not equal √36 + √64. In fact, √100 equals 10, whereas √36 + √64 equals 6 + 8, which is 14.
Understanding these misconceptions is crucial for a solid grasp of square roots and their properties. Correcting these misunderstandings can help in solving mathematical problems more accurately and efficiently.
Applications of Rational Numbers in Real Life
Rational numbers, including integers, fractions, and terminating or repeating decimals, play a vital role in various real-life applications. Below are some detailed examples showcasing their significance:
-
Financial Transactions:
Rational numbers are used extensively in financial calculations. For instance, when calculating interest rates, loan payments, and budgeting, rational numbers ensure precise and accurate financial planning.
-
Engineering and Construction:
Measurements and calculations in engineering and construction often involve rational numbers. For example, determining the dimensions of materials, calculating areas and volumes, and ensuring structural integrity require precise rational values.
-
Cooking and Recipes:
Rational numbers are used in cooking to measure ingredients accurately. For instance, recipes often call for fractions like 1/2 cup of sugar or 3/4 teaspoon of salt, ensuring consistency and taste in culinary creations.
-
Science and Medicine:
In scientific experiments and medical dosages, rational numbers are crucial. Accurate measurements of chemicals, medication dosages, and recording data rely on rational numbers for precision and safety.
-
Education and Academia:
Rational numbers are fundamental in mathematics education. They are used in teaching basic arithmetic, algebra, and advanced mathematical concepts, helping students understand the properties and applications of numbers.
-
Daily Life:
In everyday activities, rational numbers are indispensable. Whether it's dividing a pizza among friends, calculating travel time, or measuring distances, rational numbers facilitate accurate and fair distribution and estimation.
These examples demonstrate how rational numbers are integrated into various aspects of daily life, highlighting their importance in ensuring accuracy, precision, and consistency in numerous fields.
Conclusion: The Rationality of Square Root of 36
To conclude, the square root of 36 is a rational number. This conclusion is drawn based on the definition and properties of rational and irrational numbers.
Firstly, a rational number is any number that can be expressed as the quotient or fraction p/q of two integers, where p and q are integers and q is not zero. In contrast, an irrational number cannot be expressed as a simple fraction and has a non-repeating, non-terminating decimal expansion.
Given that 36 is a perfect square, its square root is an integer. The square root of 36 is 6, which can be written as 6/1, fitting the definition of a rational number. Therefore, since 6 can be expressed as a ratio of two integers, the square root of 36 is rational.
In summary:
- 36 is a perfect square.
- The square root of 36 is 6.
- 6 can be expressed as the fraction 6/1.
- Therefore, the square root of 36 is a rational number.
This understanding is fundamental in mathematics and helps clarify the nature of numbers and their classifications.

Video giải thích tại sao căn bậc hai của 36 chỉ là 6 dương. Tìm hiểu thêm về lý do và tính hợp lý của kết quả này.
Tại sao căn bậc hai của 36 chỉ là 6 dương
READ MORE:
Video giải thích về căn bậc hai của 36. Tìm hiểu tính hợp lý và tính toán của kết quả này.
Căn Bậc Hai 36