Topic what is a square + b square: Discover the significance of "a square + b square" in mathematics, a fundamental concept with diverse applications in algebra, geometry, and beyond. Learn how this simple yet powerful expression plays a crucial role in various mathematical problems and real-world scenarios. Explore its properties, uses, and examples to deepen your understanding and appreciation of this essential formula.
Table of Content
- The Formula for \(a^2 + b^2\)
- Introduction to a2 + b2
- Mathematical Definition and Notation
- Historical Context and Origin
- Properties of a2 + b2
- Applications in Geometry
- Applications in Algebra
- Applications in Calculus
- Relationship to Pythagorean Theorem
- Use in Distance Formula
- Algebraic Identities Involving a2 + b2
- Graphical Interpretation
- Examples and Practice Problems
- Advanced Applications in Mathematics
- Real-World Applications
- Common Misconceptions
- Summary and Conclusion
- YOUTUBE: Xem video để tìm hiểu công thức của a² + b² do thầy Tarun giảng dạy. Bài giảng chi tiết và dễ hiểu sẽ giúp bạn nắm vững kiến thức.
The Formula for \(a^2 + b^2\)
The expression \(a^2 + b^2\) is a common mathematical term, often encountered in various areas of mathematics including algebra, geometry, and calculus. Below is a detailed explanation of its significance and applications.
Definition
The expression \(a^2 + b^2\) represents the sum of the squares of two variables, \(a\) and \(b\). Mathematically, it is written as:
\[ a^2 + b^2 \]
Applications
- Pythagorean Theorem: In a right-angled triangle, the sum of the squares of the two legs is equal to the square of the hypotenuse. \[ c^2 = a^2 + b^2 \]
- Distance Formula: The distance \(d\) between two points \((x_1, y_1)\) and \((x_2, y_2)\) in a coordinate plane is given by: \[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
- Algebraic Identities: Used in expanding and simplifying expressions, particularly in polynomial operations.
Properties
- Non-negativity: Since squares of real numbers are always non-negative, \(a^2 \geq 0\) and \(b^2 \geq 0\), thus \(a^2 + b^2 \geq 0\).
- Symmetry: The expression is symmetric with respect to \(a\) and \(b\); that is, \(a^2 + b^2 = b^2 + a^2\).
- Invariant under Sign Change: The value of \(a^2 + b^2\) remains the same if \(a\) and \(b\) are replaced by \(-a\) and \(-b\).
Examples
- If \(a = 3\) and \(b = 4\), then: \[ a^2 + b^2 = 3^2 + 4^2 = 9 + 16 = 25 \]
- If \(a = 5\) and \(b = 12\), then: \[ a^2 + b^2 = 5^2 + 12^2 = 25 + 144 = 169 \]
Graphical Representation
In a Cartesian coordinate system, the equation \(x^2 + y^2 = r^2\) represents a circle centered at the origin with radius \(r\). This is a direct application of the formula \(a^2 + b^2\).
For example, the circle with radius 5 can be represented by:
\[
x^2 + y^2 = 25
\]
READ MORE:
Introduction to a2 + b2
The expression \(a^2 + b^2\) is a fundamental concept in mathematics, representing the sum of the squares of two variables, \(a\) and \(b\). This formula appears in various branches of mathematics and has significant applications in algebra, geometry, and beyond.
Here, we will explore the basic definition, properties, and applications of \(a^2 + b^2\), along with some illustrative examples to deepen our understanding.
- Definition:
The term \(a^2 + b^2\) refers to adding the square of \(a\) to the square of \(b\). Mathematically, it is written as:
\[
a^2 + b^2
\]
where \(a\) and \(b\) are real numbers. - Properties:
- Non-negativity: Both \(a^2\) and \(b^2\) are non-negative because the square of any real number is always non-negative. Therefore, \(a^2 + b^2 \geq 0\).
- Symmetry: The expression is symmetric with respect to \(a\) and \(b\), meaning \(a^2 + b^2 = b^2 + a^2\).
- Invariant under Sign Change: The value of \(a^2 + b^2\) remains unchanged if \(a\) and \(b\) are replaced with \(-a\) and \(-b\).
- Applications:
- Pythagorean Theorem: In a right-angled triangle, the sum of the squares of the two legs equals the square of the hypotenuse. \[ c^2 = a^2 + b^2 \]
- Distance Formula: The distance \(d\) between two points \((x_1, y_1)\) and \((x_2, y_2)\) in a coordinate plane is given by: \[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
- Algebraic Identities: Used in expanding and simplifying expressions, such as: \[ (a + b)^2 = a^2 + 2ab + b^2 \]
- Examples:
- If \(a = 3\) and \(b = 4\), then: \[ a^2 + b^2 = 3^2 + 4^2 = 9 + 16 = 25 \]
- If \(a = 5\) and \(b = 12\), then: \[ a^2 + b^2 = 5^2 + 12^2 = 25 + 144 = 169 \]
Mathematical Definition and Notation
The expression \(a^2 + b^2\) is a fundamental mathematical formula representing the sum of the squares of two variables, \(a\) and \(b\). This notation is widely used in various branches of mathematics, including algebra, geometry, and trigonometry. Below is a detailed explanation of its definition and notation.
- Definition:
The term \(a^2 + b^2\) is defined as the addition of the square of \(a\) and the square of \(b\). It is mathematically written as:
\[
a^2 + b^2
\]
where \(a\) and \(b\) are any real numbers. The squares of \(a\) and \(b\) are calculated by multiplying each number by itself:
\[
a^2 = a \times a \quad \text{and} \quad b^2 = b \times b
\]
Thus, \(a^2 + b^2\) represents:
\[
a^2 + b^2 = (a \times a) + (b \times b)
\] - Notation:
The notation \(a^2 + b^2\) uses the exponentiation symbol (^2) to denote squaring. The symbol "+" signifies the addition of the two squared terms. This notation is concise and conveys the operation of squaring and summing clearly and efficiently.
- Properties:
- Commutative Property: The order of the terms does not affect the result: \[ a^2 + b^2 = b^2 + a^2 \]
- Associative Property: Although not directly applicable to two terms, this property ensures consistency when extending the expression to more terms.
- Non-negative Result: Since squares of real numbers are always non-negative, the sum \(a^2 + b^2\) is also non-negative: \[ a^2 \geq 0 \quad \text{and} \quad b^2 \geq 0 \quad \implies \quad a^2 + b^2 \geq 0 \]
- Applications:
- Geometry: Used in the Pythagorean theorem to relate the sides of a right triangle: \[ c^2 = a^2 + b^2 \]
- Algebra: Appears in various algebraic identities and formulas, such as: \[ (a + b)^2 = a^2 + 2ab + b^2 \]
- Trigonometry: Utilized in trigonometric identities involving sine and cosine functions.
Historical Context and Origin
The expression \(a^2 + b^2\) has a rich historical background, dating back to ancient civilizations that laid the foundations for modern mathematics. Its origins can be traced through the development of mathematical theories and theorems, particularly in geometry and algebra.
- Ancient Civilizations:
Early records of squared terms appear in Babylonian mathematics around 1800 BCE, where they used geometric methods to solve quadratic equations. The Babylonians had an understanding of areas and squares, which contributed to the later formalization of the concept.
- Greek Mathematics:
The Greeks, particularly Pythagoras (c. 570–495 BCE), made significant contributions to the understanding of squared terms. The Pythagorean Theorem, one of the most well-known geometric principles, states that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides:
\[
c^2 = a^2 + b^2
\]
This theorem has been fundamental in the study of geometry and the application of squared terms. - Indian Mathematics:
Indian mathematicians like Brahmagupta (598–668 CE) also explored the properties of squares. In his work, Brahmagupta provided rules for arithmetic operations involving squared terms and solutions to quadratic equations.
- Islamic Golden Age:
During the Islamic Golden Age (8th to 14th centuries), mathematicians like Al-Khwarizmi further developed algebraic methods involving squares. His work on solving quadratic equations was influential in the evolution of algebra.
- European Renaissance:
In the European Renaissance, mathematicians such as René Descartes (1596–1650) and Pierre de Fermat (1607–1665) advanced the study of algebra and geometry, including the manipulation and understanding of squared terms. Descartes' Cartesian coordinate system and Fermat's work on analytic geometry incorporated \(a^2 + b^2\) in various contexts.
- Modern Mathematics:
Today, the expression \(a^2 + b^2\) is ubiquitous in mathematics. It is a fundamental component of many formulas and theorems across different branches of mathematics, reflecting its deep-rooted historical significance and continuous relevance.
Properties of a2 + b2
The expression \(a^2 + b^2\) possesses several important mathematical properties. These properties are fundamental in understanding its behavior and applications across various mathematical contexts. Below, we explore these properties in detail.
- Commutative Property:
The sum of the squares is commutative, meaning the order of the terms does not affect the result:
\[
a^2 + b^2 = b^2 + a^2
\] - Associative Property:
Although this property is more relevant in the context of addition involving multiple terms, it ensures the consistent behavior of summing squares in any grouping:
\[
(a^2 + b^2) + c^2 = a^2 + (b^2 + c^2)
\] - Non-negativity:
Both \(a^2\) and \(b^2\) are non-negative because squaring any real number results in a non-negative value. Therefore, the sum \(a^2 + b^2\) is also non-negative:
\[
a^2 \geq 0 \quad \text{and} \quad b^2 \geq 0 \quad \implies \quad a^2 + b^2 \geq 0
\] - Zero Property:
The sum \(a^2 + b^2\) equals zero if and only if both \(a\) and \(b\) are zero:
\[
a^2 + b^2 = 0 \quad \iff \quad a = 0 \quad \text{and} \quad b = 0
\] - Symmetry:
The expression \(a^2 + b^2\) is symmetric with respect to \(a\) and \(b\), meaning it remains unchanged if \(a\) and \(b\) are swapped:
\[
a^2 + b^2 = b^2 + a^2
\] - Invariant under Sign Change:
The value of \(a^2 + b^2\) remains the same if \(a\) and \(b\) are replaced with \(-a\) and \(-b\):
\[
a^2 + b^2 = (-a)^2 + (-b)^2
\] - Extension to Higher Dimensions:
This property can be generalized to higher dimensions. For example, the sum of the squares of three variables \(a\), \(b\), and \(c\) is:
\[
a^2 + b^2 + c^2
\]
Applications in Geometry
The expression \(a^2 + b^2\) is widely used in geometry, forming the basis of several key theorems and formulas. Below, we explore its various applications in geometry, illustrating its importance and versatility.
- Pythagorean Theorem:
The Pythagorean Theorem is one of the most famous applications of \(a^2 + b^2\). It states that in a right-angled triangle, the square of the length of the hypotenuse (\(c\)) is equal to the sum of the squares of the lengths of the other two sides (\(a\) and \(b\)):
\[
c^2 = a^2 + b^2
\]
This theorem is fundamental in Euclidean geometry and is used to calculate distances and solve various geometric problems. - Distance Formula:
In a coordinate plane, the distance \(d\) between two points \((x_1, y_1)\) and \((x_2, y_2)\) is derived using the concept of \(a^2 + b^2\). The distance formula is given by:
\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]
Here, the differences in the coordinates (\(x_2 - x_1\) and \(y_2 - y_1\)) are squared and summed, demonstrating the application of \(a^2 + b^2\) in calculating the straight-line distance between two points. - Equation of a Circle:
The standard equation of a circle centered at the origin with radius \(r\) is based on the sum of squares:
\[
x^2 + y^2 = r^2
\]
This equation shows that any point \((x, y)\) on the circle satisfies the condition that the sum of the squares of its coordinates equals the square of the radius. - Ellipse and Hyperbola:
Similar to circles, the equations of ellipses and hyperbolas also involve the sum of squares. For an ellipse centered at the origin with semi-major axis \(a\) and semi-minor axis \(b\), the equation is:
\[
\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1
\]
For a hyperbola, the standard form is:
\[
\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1
\]
These equations demonstrate the application of squared terms in defining conic sections. - Vector Magnitude:
The magnitude (or length) of a vector \(\vec{v} = (a, b)\) in a 2-dimensional space is given by the square root of the sum of the squares of its components:
\[
|\vec{v}| = \sqrt{a^2 + b^2}
\]
This formula is crucial in vector analysis and physics, where it is used to determine the length of vectors and their directional properties.
Applications in Algebra
The expression \(a^2 + b^2\) is integral to many algebraic concepts and techniques. Its applications span various areas, including solving equations, simplifying expressions, and proving identities. Below, we delve into the key algebraic applications of \(a^2 + b^2\).
- Algebraic Identities:
Several fundamental algebraic identities involve \(a^2 + b^2\). These identities are useful in simplifying expressions and solving equations. Notable identities include:
\[
(a + b)^2 = a^2 + 2ab + b^2
\]
\[
(a - b)^2 = a^2 - 2ab + b^2
\]
These formulas show how \(a^2 + b^2\) appears in the expansion of binomials. - Quadratic Equations:
In solving quadratic equations, the expression \(a^2 + b^2\) often arises. For instance, the quadratic formula for solving \(ax^2 + bx + c = 0\) involves the square of terms:
\[
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\]
The discriminant (\(b^2 - 4ac\)) includes the squared term \(b^2\), highlighting the role of squares in determining the nature of the roots. - Completing the Square:
The method of completing the square transforms a quadratic expression into a perfect square trinomial. This process involves \(a^2 + b^2\) and is crucial for solving quadratic equations and analyzing their properties. For example, transforming \(ax^2 + bx + c\) into a perfect square form:
\[
ax^2 + bx + c = a(x^2 + \frac{b}{a}x) + c
\]
\[
= a \left( (x + \frac{b}{2a})^2 - \frac{b^2}{4a^2} \right) + c
\]
This shows the use of squared terms in completing the square. - Distance Formula in Coordinate Geometry:
In coordinate geometry, the distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) is found using the distance formula:
\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]
This application illustrates the use of \(a^2 + b^2\) in finding the distance between points. - Complex Numbers:
In the study of complex numbers, \(a^2 + b^2\) is used to find the magnitude of a complex number \(z = a + bi\):
\[
|z| = \sqrt{a^2 + b^2}
\]
This magnitude represents the distance of the complex number from the origin in the complex plane, showing the importance of squared terms in complex analysis.
Applications in Calculus
The expression a2 + b2 appears frequently in calculus, particularly in contexts involving optimization, polar coordinates, and integration.
1. Optimization
In optimization problems, a2 + b2 is often used to find minimum or maximum values of functions subject to constraints. For example, finding the minimum distance from a point to a curve can involve minimizing an expression of the form a2 + b2.
- Consider a function f(x, y) = a2 + b2 subject to a constraint g(x, y) = 0.
- Using the method of Lagrange multipliers, we solve ∇f = λ∇g to find critical points.
2. Polar Coordinates
In polar coordinates, the expression a2 + b2 naturally arises when converting from Cartesian coordinates. The relationship between Cartesian coordinates (x, y) and polar coordinates (r, θ) is given by:
This conversion is useful for integrating functions over circular regions.
3. Integration
In integration, a2 + b2 often appears when evaluating integrals involving trigonometric functions or in the context of double integrals over circular regions.
- For instance, to compute the integral ∫∫_R f(x, y) dA over a circular region, we switch to polar coordinates where dA = r dr dθ and use x = r cos(θ) and y = r sin(θ).
- Consider the integral of e-(x2 + y2) over all space. Using polar coordinates simplifies this to:
4. Pythagorean Identity
In trigonometric integrals, the Pythagorean identity sin2(θ) + cos2(θ) = 1 simplifies integrals involving a2 + b2.
- For example, the integral of sin2(θ) can be simplified using the identity:
- This identity helps simplify and solve many trigonometric integrals in calculus.
In conclusion, the expression a2 + b2 is fundamental in various applications within calculus, aiding in optimization, coordinate transformations, integration, and simplification of trigonometric expressions.
Relationship to Pythagorean Theorem
The relationship between \( a^2 + b^2 \) and the Pythagorean Theorem is fundamental in mathematics, especially in the study of right triangles. The Pythagorean Theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
The formula for the Pythagorean Theorem is:
\( a^2 + b^2 = c^2 \)
Where:
- \( a \) and \( b \) are the lengths of the two legs of the right triangle
- \( c \) is the length of the hypotenuse
To see this theorem in action, consider a right-angled triangle with legs of lengths 3 and 4:
- First, square the lengths of the legs: \( 3^2 = 9 \) and \( 4^2 = 16 \).
- Next, add these squares together: \( 9 + 16 = 25 \).
- Finally, find the square root of the sum to get the hypotenuse: \( \sqrt{25} = 5 \).
This demonstrates that a triangle with sides of 3, 4, and 5 units satisfies the Pythagorean Theorem, with 5 being the length of the hypotenuse.
The Pythagorean Theorem is not only a theoretical construct but also has practical applications in various fields such as:
- Architecture: Ensuring buildings have right angles and calculating distances.
- Engineering: Designing stable structures like bridges and roads.
- Physics: Calculating distances and forces in different systems.
- Navigation: Finding the shortest distance between two points.
In conclusion, the expression \( a^2 + b^2 \) is directly linked to the Pythagorean Theorem, providing a way to determine the relationship between the sides of a right triangle and find the length of the hypotenuse.

Use in Distance Formula
The distance formula is a crucial concept in geometry that helps determine the distance between two points in a Cartesian plane. This formula is closely related to the Pythagorean Theorem, as it essentially calculates the hypotenuse of a right triangle formed by the horizontal and vertical distances between two points.
In a two-dimensional space, the distance formula between two points \( P(x_1, y_1) \) and \( Q(x_2, y_2) \) is given by:
\[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
Here's how to use the distance formula step by step:
- Identify the coordinates of the two points. Let's call them \( P(x_1, y_1) \) and \( Q(x_2, y_2) \).
- Calculate the difference between the x-coordinates and y-coordinates of the points:
- \( \Delta x = x_2 - x_1 \)
- \( \Delta y = y_2 - y_1 \)
- Square these differences:
- \( (\Delta x)^2 \)
- \( (\Delta y)^2 \)
- Add the squared differences:
- \( (\Delta x)^2 + (\Delta y)^2 \)
- Take the square root of the sum to find the distance:
- \( d = \sqrt{(\Delta x)^2 + (\Delta y)^2} \)
Let's look at an example to see how the distance formula is applied:
Suppose we want to find the distance between the points \( P(1, 4) \) and \( Q(7, 12) \). Following the steps:
- Identify the coordinates:
- \( x_1 = 1, y_1 = 4 \)
- \{ x_2 = 7, y_2 = 12 \)
- Calculate the differences:
- \( \Delta x = 7 - 1 = 6 \)
- \( \Delta y = 12 - 4 = 8 \)
- Square the differences:
- \( (\Delta x)^2 = 6^2 = 36 \)
- \( (\Delta y)^2 = 8^2 = 64 \)
- Add the squares:
- \( 36 + 64 = 100 \)
- Take the square root:
- \( d = \sqrt{100} = 10 \)
Thus, the distance between the points \( P(1, 4) \) and \( Q(7, 12) \) is 10 units.
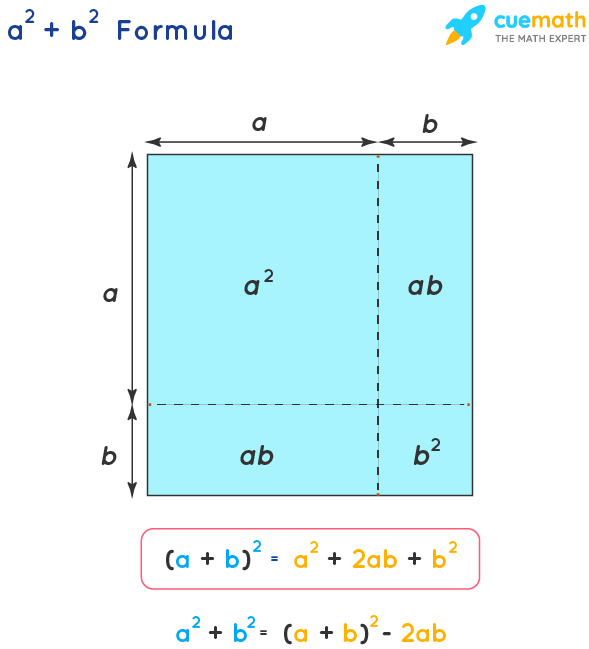
Algebraic Identities Involving a2 + b2
Algebraic identities are equations that hold true for all values of the involved variables. The identity \(a^2 + b^2\) is commonly encountered in algebra and can be used in various forms to simplify expressions and solve problems. Here are some important identities involving \(a^2 + b^2\) along with their derivations and applications:
- Sum of Squares Formula:
The sum of squares of two numbers \(a\) and \(b\) can be expressed as:
\[a^2 + b^2 = (a + b)^2 - 2ab\]This identity helps in simplifying expressions where the sum of the squares is involved.
- Difference of Squares:
Another important identity is the difference of squares:
\[a^2 - b^2 = (a + b)(a - b)\]Although not directly involving \(a^2 + b^2\), this identity is closely related and often used in conjunction with the sum of squares.
- Squared Binomial:
The square of a binomial expression leads to:
\[(a \pm b)^2 = a^2 \pm 2ab + b^2\]This identity shows how the sum or difference of two variables squared results in the sum of their squares plus or minus twice their product.
- Alternative Form:
The sum of squares can also be expressed using the difference of squares formula:
\[a^2 + b^2 = (a - b)^2 + 2ab\]This is useful in scenarios where \(a - b\) is known or easier to compute.
Below are some examples illustrating the use of these identities:
- Example 1:
Verify the identity \(a^2 + b^2 = (a + b)^2 - 2ab\) for \(a = 3\) and \(b = 4\).
\[ \begin{align*} a^2 + b^2 &= 3^2 + 4^2 = 9 + 16 = 25 \\ (a + b)^2 - 2ab &= (3 + 4)^2 - 2(3)(4) = 7^2 - 24 = 49 - 24 = 25 \end{align*} \]Thus, the identity holds true.
- Example 2:
Expand and simplify \((x - y)^2 + 2xy\).
\[ (x - y)^2 + 2xy = x^2 - 2xy + y^2 + 2xy = x^2 + y^2 \]This confirms the alternative form of the sum of squares.
- Example 3:
Find \(a^2 + b^2\) for \(a = 5\) and \(b = 6\) using the sum of squares formula.
\[ a^2 + b^2 = (5 + 6)^2 - 2(5)(6) = 11^2 - 60 = 121 - 60 = 61 \]
These identities and examples demonstrate the utility and versatility of algebraic identities involving \(a^2 + b^2\) in simplifying expressions and solving mathematical problems.
Graphical Interpretation
The expression \(a^2 + b^2\) has several important graphical interpretations, particularly in the context of geometry and algebra. Below, we explore some of these interpretations.
1. Interpretation in the Cartesian Plane
In a Cartesian coordinate system, the expression \(a^2 + b^2\) can be visualized as the square of the distance from the origin \((0,0)\) to a point \((a,b)\). This is derived from the distance formula:
\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]
Setting \((x_1, y_1) = (0,0)\) and \((x_2, y_2) = (a,b)\), we get:
\[
d = \sqrt{a^2 + b^2}
\]
This shows that \(a^2 + b^2\) represents the square of the distance from the origin to the point \((a,b)\).
2. Circle Equation
The equation of a circle centered at the origin with radius \(r\) is given by:
\[
x^2 + y^2 = r^2
\]
Here, \(a\) and \(b\) can be considered as \(x\) and \(y\), respectively. Therefore, the equation \(a^2 + b^2 = r^2\) describes a circle with radius \(r\) in the Cartesian plane.
3. Relationship with Pythagorean Theorem
Graphically, \(a^2 + b^2\) is directly related to the Pythagorean Theorem. In a right triangle with legs of lengths \(a\) and \(b\), and hypotenuse \(c\), the theorem states:
\[
a^2 + b^2 = c^2
\]
This geometric interpretation shows that \(a^2 + b^2\) represents the sum of the squares of the legs of the right triangle, equating to the square of the hypotenuse.
4. Graphing Quadratic Forms
When graphing quadratic forms such as \(a^2 + b^2\), we obtain a paraboloid in three-dimensional space. This can be visualized using graphing tools like Desmos or other graphing calculators. For instance, plotting \(z = a^2 + b^2\) gives a surface that opens upwards.
Here's how to graph this surface using Desmos:
- Open the .
- Enter the equation \(z = a^2 + b^2\) in the input field.
- Visualize the 3D surface representing this quadratic form.
5. Visualizing Linear Transformations
Linear transformations involving \(a^2 + b^2\) can be visualized as transformations of geometric shapes. For example, rotating or scaling vectors in the plane can change the representation of \(a\) and \(b\), but the value of \(a^2 + b^2\) remains invariant under these transformations.
To better understand these transformations, consider the vector \((a,b)\) and how it changes under rotation by an angle \(\theta\). The new coordinates \((a', b')\) are given by:
\[
a' = a \cos \theta - b \sin \theta
\]
\]
\[
b' = a \sin \theta + b \cos \theta
\]
Despite this rotation, the value \(a'^2 + b'^2 = a^2 + b^2\) remains constant.
Understanding these graphical interpretations of \(a^2 + b^2\) enhances our comprehension of its role in various mathematical contexts, from basic geometry to advanced linear algebra and calculus.
Examples and Practice Problems
Practicing problems involving the expression \(a^2 + b^2\) helps in understanding its application in various algebraic contexts. Here are some examples and practice problems to solidify your understanding:
Example 1: Simplify the Expression
Simplify the expression \((3x + 4y)^2\).
Solution:
- Identify \(a = 3x\) and \(b = 4y\).
- Use the identity \((a + b)^2 = a^2 + 2ab + b^2\).
- Substitute the values: \[ (3x + 4y)^2 = (3x)^2 + 2(3x)(4y) + (4y)^2 \]
- Calculate each term: \[ (3x)^2 = 9x^2, \quad 2(3x)(4y) = 24xy, \quad (4y)^2 = 16y^2 \]
- Combine the terms: \[ (3x + 4y)^2 = 9x^2 + 24xy + 16y^2 \]
Example 2: Factorize the Expression
Factorize the expression \(49x^2 + 36y^2\).
Solution:
- Recognize the expression as a sum of squares: \[ 49x^2 = (7x)^2 \quad \text{and} \quad 36y^2 = (6y)^2 \]
- Thus, the expression can be written as: \[ 49x^2 + 36y^2 = (7x)^2 + (6y)^2 \]
Practice Problems
- Simplify the expression \((5a - 2b)^2\).
- Factorize \(25m^2 + 16n^2\).
- Compute the value of \(a^2 + b^2\) for \(a = 8\) and \(b = 15\).
These examples and problems illustrate the use of the identity \(a^2 + b^2\) in simplifying expressions and factoring sums of squares. Practice these to gain confidence in handling various algebraic identities.
Advanced Applications in Mathematics
The expression \(a^2 + b^2\) has numerous advanced applications in various branches of mathematics, beyond its foundational role in the Pythagorean theorem. Here are some key advanced applications:
-
Complex Numbers
In complex number theory, a complex number is often represented as \(z = a + bi\), where \(i\) is the imaginary unit. The modulus (or absolute value) of a complex number, which represents its distance from the origin in the complex plane, is given by:
\[
|z| = \sqrt{a^2 + b^2}
\]This expression is crucial in operations involving complex numbers, such as finding powers and roots, and in analyzing their properties.
-
Fourier Transforms
The Fourier transform is a powerful tool in signal processing and analysis, converting functions from the time domain to the frequency domain. For a given function \(f(x)\), its Fourier transform \(\hat{f}(\xi)\) often involves terms of the form \(a^2 + b^2\) when dealing with sinusoidal components:
\[
\hat{f}(\xi) = \int_{-\infty}^{\infty} f(x) e^{-2\pi i x \xi} \, dx
\]The magnitude of the Fourier transform, which is used to analyze the frequency components of signals, is represented as:
\[
|\hat{f}(\xi)| = \sqrt{(\Re \hat{f}(\xi))^2 + (\Im \hat{f}(\xi))^2}
\] -
Vector Magnitudes
In vector calculus, the magnitude (or length) of a vector in two-dimensional space is found using the formula \(a^2 + b^2\). For a vector \(\mathbf{v} = \langle a, b \rangle\), the magnitude is given by:
\[
|\mathbf{v}| = \sqrt{a^2 + b^2}
\]This is essential in various applications, including physics, engineering, and computer graphics.
-
Least Squares Method
In statistics and data fitting, the least squares method minimizes the sum of the squares of the residuals (the differences between observed and predicted values). For a set of data points \((x_i, y_i)\) and a model \(y = mx + c\), the objective function to be minimized is:
\[
S = \sum_{i=1}^{n} (y_i - (mx_i + c))^2
\]This involves finding the best-fit line by minimizing the expression \(a^2 + b^2\) over all data points.
-
Elliptic Integrals
Elliptic integrals arise in various problems in physics and engineering, including computing arc lengths of ellipses and solving pendulum motion equations. They often involve expressions of the form \(a^2 + b^2\) in their integrands:
\[
F(\phi, k) = \int_{0}^{\phi} \frac{d\theta}{\sqrt{1 - k^2 \sin^2 \theta}}
\]where \(k\) is the modulus of the elliptic integral.
Real-World Applications
The expression \(a^2 + b^2\) has several important real-world applications across various fields such as physics, engineering, computer science, and finance. Understanding these applications helps in solving practical problems and optimizing solutions. Here are some detailed examples of real-world applications:
- Physics and Engineering:
In physics, \(a^2 + b^2\) is often used in the context of vector magnitudes. When dealing with vectors in two-dimensional space, the magnitude of the resultant vector is given by \(\sqrt{a^2 + b^2}\). This is crucial for calculating forces, velocities, and other vector quantities in mechanics and electromagnetism.
- Signal Processing:
In signal processing, \(a^2 + b^2\) appears in the calculation of the power of a signal. For a signal with components \(a\) and \(b\), the power is proportional to the sum of the squares of these components. This is important for analyzing and filtering signals in telecommunications and audio engineering.
- Computer Graphics:
In computer graphics, the distance between two points on a screen is computed using the formula \(\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\). Here, the terms \((x_2 - x_1)^2\) and \((y_2 - y_1)^2\) represent \(a^2\) and \(b^2\) respectively. This calculation is fundamental for rendering images and animations.
- Finance:
In finance, the formula is used to calculate the risk (variance) of a portfolio of investments. If \(a\) and \(b\) are the returns of two different assets, then \(a^2 + b^2\) can be part of the formula to determine the overall risk, helping investors to optimize their portfolios.
- Navigation and Geolocation:
For navigation purposes, \(a^2 + b^2\) is used in the Pythagorean theorem to calculate distances between points on a map. This is vital for GPS systems, enabling accurate positioning and routing.
These examples illustrate the diverse applications of the \(a^2 + b^2\) formula, highlighting its significance in both theoretical and practical scenarios.
Common Misconceptions
Understanding a2 + b2 involves recognizing several common misconceptions that often arise in mathematics education. Here are some of the most frequent misunderstandings:
-
Misinterpreting the Formula: One frequent misconception is misinterpreting the relationship between the sum of the squares and the lengths of the sides in various geometric contexts. For instance, students might incorrectly apply the Pythagorean theorem in non-right-angled triangles.
-
Reversing the Pythagorean Theorem: Some learners mistakenly believe that if a2 + b2 = c2, then a, b, and c must be the sides of a right triangle. While this is true in a right triangle, it does not imply that any three lengths satisfying this equation form a right triangle.
-
Overgeneralizing the Distance Formula: Students often confuse the distance formula in coordinate geometry with other uses of squares. The formula d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} is specific to finding the distance between two points in a plane and should not be applied arbitrarily.
-
Errors in Completing the Square: Completing the square is another area where misconceptions occur. Students may forget to add or subtract the necessary constant term, leading to incorrect solutions. Properly understanding the process and its purpose can help mitigate this error.
-
Misunderstanding Geometric Interpretations: Misconceptions also arise in the geometric interpretation of a2 + b2. For example, some might incorrectly assume that the areas represented by these terms always form a perfect square.
To address these misconceptions, it is crucial to emphasize the underlying concepts and provide varied practice problems. Visual aids and manipulatives can also be beneficial in helping students grasp these ideas more concretely.
Summary and Conclusion
The expression \(a^2 + b^2\) is fundamental in various branches of mathematics, particularly in geometry, algebra, and calculus. Its significance can be traced through numerous applications and mathematical identities, highlighting its versatility and importance.
In geometry, \(a^2 + b^2\) is pivotal in understanding the Pythagorean theorem, which establishes the relationship between the sides of a right-angled triangle. This theorem is not only a cornerstone in Euclidean geometry but also provides the basis for calculating distances in various contexts, including real-world applications such as navigation and engineering.
Algebraically, the expression appears in identities and equations that simplify and solve complex problems. For example, the sum of squares formula and the distance formula are directly derived from this expression, showcasing its utility in simplifying computations and deriving solutions.
In calculus, \(a^2 + b^2\) is essential for understanding curves and surfaces. It appears in the equations of circles and spheres, and in integral calculations, aiding in the comprehension of geometric properties and volumes.
Beyond theoretical mathematics, \(a^2 + b^2\) has real-world applications in physics, engineering, and computer science. It is used to calculate forces, trajectories, and optimizations in various technological advancements, illustrating the practical impact of this mathematical concept.
Overall, the exploration of \(a^2 + b^2\) reveals its profound influence across multiple disciplines. Its presence in fundamental theories, practical applications, and advanced mathematical concepts underscores its importance as a versatile and powerful tool in mathematics.
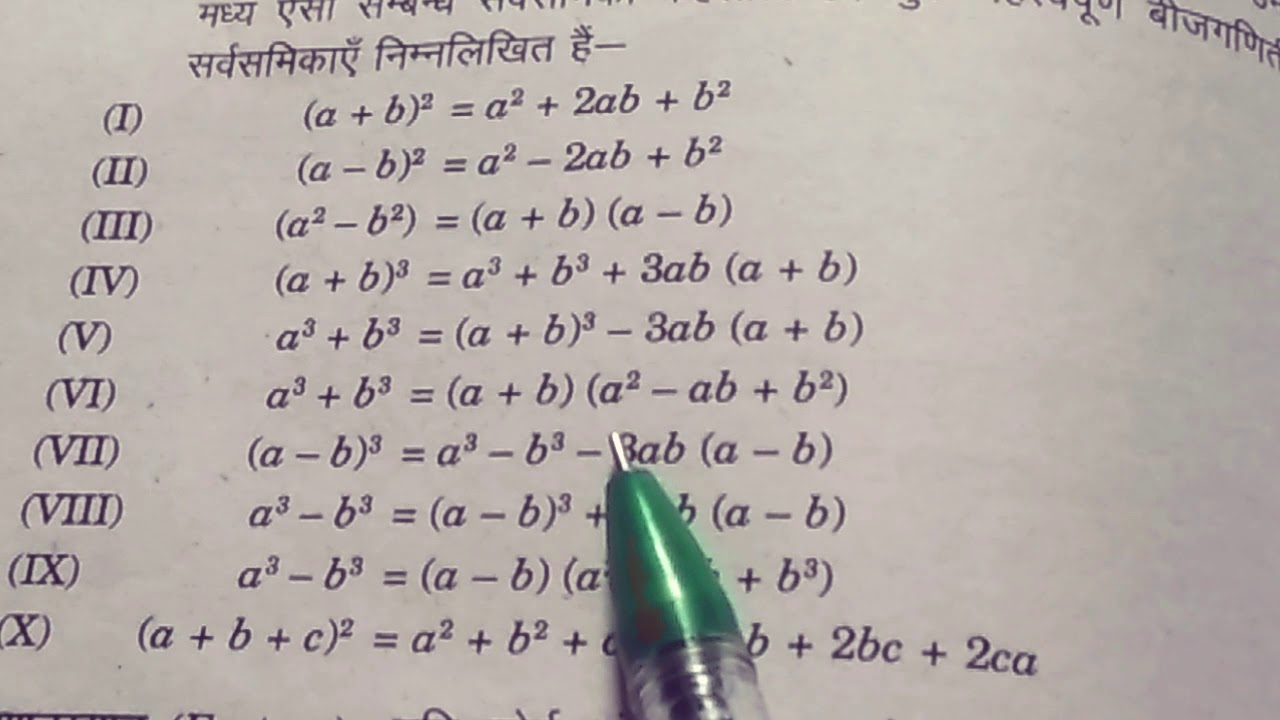
READ MORE:
Xem video để tìm hiểu công thức của a² + b² do thầy Tarun giảng dạy. Bài giảng chi tiết và dễ hiểu sẽ giúp bạn nắm vững kiến thức.
Công thức của a² + b² | Tarun thầy giáo