Topic what is square root of 63: What is the square root of 63? Uncover the fascinating details behind this intriguing number, its decimal approximation, and its significance in various fields such as mathematics, engineering, and science. Learn how to simplify it in radical form and explore its applications and graphical representations to deepen your understanding.
Table of Content
- Square Root of 63
- Introduction to Square Roots
- Understanding the Square Root of 63
- Mathematical Properties of the Square Root of 63
- Decimal Representation of the Square Root of 63
- Simplified Radical Form of the Square Root of 63
- Prime Factorization Method
- Applications in Mathematics
- Applications in Engineering
- Applications in Science
- Graphical Representation of the Square Root of 63
- Approximation Techniques
- Comparison with Other Square Roots
- Common Misconceptions
- Frequently Asked Questions
- Conclusion
- YOUTUBE: Khám phá cách tính và ứng dụng của căn bậc hai của 63 trong toán học, kỹ thuật và khoa học.
Square Root of 63
The square root of 63 is an irrational number, meaning it cannot be expressed as a simple fraction. The value of the square root of 63 is approximately:
\[\sqrt{63} \approx 7.937\]
Decimal Form
The approximate value of \(\sqrt{63}\) in decimal form is:
\[\sqrt{63} \approx 7.937253933\]
Simplified Radical Form
To express the square root of 63 in its simplest radical form, we can break it down into its prime factors:
\[63 = 3^2 \times 7\]
Therefore, the square root of 63 can be simplified as:
\[\sqrt{63} = \sqrt{3^2 \times 7} = 3\sqrt{7}\]
Applications and Examples
- Mathematics: Used in various mathematical calculations and geometric problems.
- Engineering: Useful in solving problems involving quadratic equations and areas.
- Science: Applied in physics and other sciences for precise measurements and computations.
Table of Square Roots Near 63
| Number | Square Root |
| 60 | \(\sqrt{60} \approx 7.745\) |
| 61 | \(\sqrt{61} \approx 7.810\) |
| 62 | \(\sqrt{62} \approx 7.874\) |
| 63 | \(\sqrt{63} \approx 7.937\) |
| 64 | \(\sqrt{64} = 8\) |
| 65 | \(\sqrt{65} \approx 8.062\) |
READ MORE:
Introduction to Square Roots
The concept of square roots is fundamental in mathematics. The square root of a number is a value that, when multiplied by itself, gives the original number. For instance, the square root of 9 is 3 because \(3 \times 3 = 9\). Square roots are widely used in various branches of mathematics, engineering, and science.
Mathematically, the square root of a number \(x\) is represented as \(\sqrt{x}\). For any non-negative number \(x\), there exists a non-negative number \(y\) such that:
\[y = \sqrt{x}\]
Key properties of square roots include:
- Non-Negativity: The square root of a non-negative number is also non-negative.
- Product Property: The square root of a product is the product of the square roots of the factors: \(\sqrt{ab} = \sqrt{a} \times \sqrt{b}\).
- Quotient Property: The square root of a quotient is the quotient of the square roots: \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\), where \(b \neq 0\).
Square roots can be classified into two main categories:
- Perfect Squares: These are numbers whose square roots are integers. Examples include 1, 4, 9, 16, 25, etc.
- Non-Perfect Squares: These are numbers whose square roots are irrational, meaning they cannot be expressed as a simple fraction. Examples include 2, 3, 5, 7, 10, etc.
The square root function is also pivotal in solving quadratic equations. Given a quadratic equation of the form:
\[ax^2 + bx + c = 0\]
The solutions can be found using the quadratic formula, which involves the square root operation:
\[x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\]
Understanding square roots enhances our ability to solve various mathematical problems, analyze geometric properties, and apply these concepts in real-world scenarios.
Understanding the Square Root of 63
The square root of 63 is a number that, when multiplied by itself, equals 63. In mathematical notation, this is expressed as:
\[\sqrt{63}\]
The square root of 63 is an irrational number, meaning it cannot be exactly represented as a simple fraction and its decimal representation is non-repeating and non-terminating. The approximate value of the square root of 63 is:
\[\sqrt{63} \approx 7.937253933\]
Simplified Radical Form
The square root of 63 can be simplified by breaking down the number into its prime factors. The prime factorization of 63 is:
\[63 = 3^2 \times 7\]
Using this factorization, the square root of 63 can be simplified as follows:
\[\sqrt{63} = \sqrt{3^2 \times 7} = 3\sqrt{7}\]
Thus, the simplified radical form of the square root of 63 is \(3\sqrt{7}\).
Decimal and Fractional Approximations
While the exact value of \(\sqrt{63}\) is an irrational number, we can use its decimal approximation for practical purposes. For example:
- In decimal form: \(\sqrt{63} \approx 7.937\)
- In fractional form: \(\sqrt{63} \approx \frac{7937}{1000}\)
Applications of \(\sqrt{63}\)
The square root of 63 finds applications in various fields, including:
- Mathematics: Used in solving quadratic equations and in geometric calculations.
- Engineering: Applied in calculations involving areas, volumes, and other measurements.
- Science: Essential in physics and other scientific computations for precise measurements.
Table of Square Roots Near 63
For a better understanding, here is a table of square roots of numbers close to 63:
| Number | Square Root |
| 60 | \(\sqrt{60} \approx 7.745\) |
| 61 | \(\sqrt{61} \approx 7.810\) |
| 62 | \(\sqrt{62} \approx 7.874\) |
| 63 | \(\sqrt{63} \approx 7.937\) |
| 64 | \(\sqrt{64} = 8\) |
| 65 | \(\sqrt{65} \approx 8.062\) |
By understanding the square root of 63 and its applications, we can appreciate the role it plays in various mathematical and real-world contexts.
Mathematical Properties of the Square Root of 63
The square root of 63 has several interesting mathematical properties that make it significant in various calculations and applications. Understanding these properties provides insight into its behavior and usefulness in different contexts.
Irrational Nature
The square root of 63 is an irrational number, meaning it cannot be exactly expressed as a fraction of two integers. Its decimal representation is non-terminating and non-repeating:
\[\sqrt{63} \approx 7.937253933\]
Simplification
The prime factorization of 63 is:
\[63 = 3^2 \times 7\]
Using this, the square root of 63 can be simplified as:
\[\sqrt{63} = \sqrt{3^2 \times 7} = 3\sqrt{7}\]
This simplified radical form is useful for exact calculations and in solving equations.
Properties of Square Roots
- Non-Negativity: The square root of any non-negative number is non-negative. Thus, \(\sqrt{63}\) is positive.
- Product Property: The square root of a product is the product of the square roots of the factors: \[\sqrt{ab} = \sqrt{a} \times \sqrt{b}\] For example: \[\sqrt{63 \times 2} = \sqrt{126} = \sqrt{63} \times \sqrt{2}\]
- Quotient Property: The square root of a quotient is the quotient of the square roots: \[\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\] For example: \[\sqrt{\frac{63}{9}} = \sqrt{7} = \frac{\sqrt{63}}{\sqrt{9}} = \frac{\sqrt{63}}{3}\]
Applications
The properties of the square root of 63 make it useful in various applications:
- Solving Quadratic Equations: The square root function is essential in solving equations of the form \(ax^2 + bx + c = 0\).
- Geometry: Square roots are used to calculate distances, areas, and other geometric properties.
- Engineering: Square roots are used in formulas for stress, strain, and other physical properties.
Example Calculation
Consider the quadratic equation:
\[x^2 - 63 = 0\]
To solve for \(x\), we take the square root of both sides:
\[x = \pm \sqrt{63}\]
This shows that the solutions to the equation are \(x = \sqrt{63}\) and \(x = -\sqrt{63}\).
Comparison with Other Square Roots
Understanding how \(\sqrt{63}\) compares with other square roots can be insightful. Here is a comparison table:
| Number | Square Root |
| 60 | \(\sqrt{60} \approx 7.745\) |
| 61 | \(\sqrt{61} \approx 7.810\) |
| 62 | \(\sqrt{62} \approx 7.874\) |
| 63 | \(\sqrt{63} \approx 7.937\) |
| 64 | \(\sqrt{64} = 8\) |
| 65 | \(\sqrt{65} \approx 8.062\) |
By exploring these properties and comparisons, we gain a deeper understanding of the mathematical significance of the square root of 63.
Decimal Representation of the Square Root of 63
The square root of 63, being an irrational number, cannot be expressed exactly as a finite decimal or a simple fraction. However, its decimal representation provides a useful approximation for practical calculations. The decimal form of \(\sqrt{63}\) is:
\[\sqrt{63} \approx 7.937253933\]
This approximation is often rounded to a certain number of decimal places depending on the level of precision required. Commonly, \(\sqrt{63}\) is rounded to three decimal places:
\[\sqrt{63} \approx 7.937\]
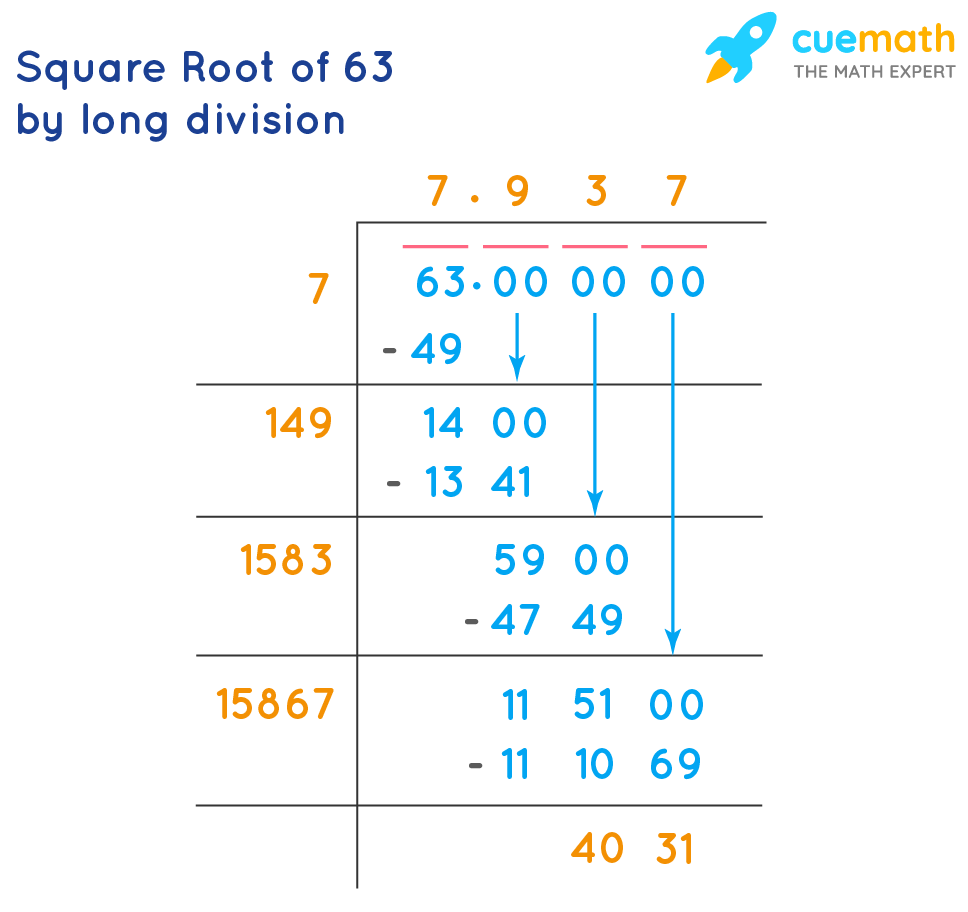
Calculating Decimal Representation
The decimal value of the square root of 63 can be computed using various methods such as long division, approximation algorithms, or by using a calculator. Here's a step-by-step approach using the long division method:
- Pair the digits of 63 from the decimal point, adding zeros if necessary (63.000000).
- Find the largest number whose square is less than or equal to 63. This number is 7 because \(7^2 = 49\) and \(8^2 = 64\).
- Subtract \(49\) from \(63\) to get \(14\), and bring down the next pair of zeros (making it 1400).
- Double the number 7 to get 14, and determine how many times 14 can fit into 1400 when considering the next digit. Continue the process to refine the approximation.
Examples of Approximations
For various levels of precision, the square root of 63 can be approximated as follows:
- 1 decimal place: \(\sqrt{63} \approx 7.9\)
- 2 decimal places: \(\sqrt{63} \approx 7.94\)
- 3 decimal places: \(\sqrt{63} \approx 7.937\)
- 4 decimal places: \(\sqrt{63} \approx 7.9373\)
Comparison with Other Square Roots
To understand the position of \(\sqrt{63}\) among other square roots, here is a comparison table with numbers close to 63:
| Number | Square Root (approx.) |
| 60 | \(\sqrt{60} \approx 7.745\) |
| 61 | \(\sqrt{61} \approx 7.810\) |
| 62 | \(\sqrt{62} \approx 7.874\) |
| 63 | \(\sqrt{63} \approx 7.937\) |
| 64 | \(\sqrt{64} = 8\) |
| 65 | \(\sqrt{65} \approx 8.062\) |
Understanding the decimal representation of the square root of 63 helps in making precise calculations and comparisons in various mathematical and practical applications.

Simplified Radical Form of the Square Root of 63
To simplify the square root of 63, we need to express it in its simplest radical form. This involves breaking down the number into its prime factors and simplifying the expression where possible.
Step-by-Step Simplification Process
- Find the Prime Factorization:
The first step is to determine the prime factorization of 63. The prime factors of 63 are:
\[63 = 3^2 \times 7\]
- Group the Prime Factors:
Next, we group the prime factors in pairs where possible. In this case, we have a pair of 3s:
\[63 = (3 \times 3) \times 7 = 3^2 \times 7\]
- Apply the Square Root to Each Group:
We then apply the square root to each group of prime factors. The square root of \(3^2\) is 3:
\[\sqrt{63} = \sqrt{3^2 \times 7} = \sqrt{3^2} \times \sqrt{7} = 3\sqrt{7}\]
Thus, the simplified radical form of the square root of 63 is:
\[\sqrt{63} = 3\sqrt{7}\]
Verification of the Simplified Form
To verify the simplification, we can square the simplified form and check if we get back the original number:
\[(3\sqrt{7})^2 = 3^2 \times (\sqrt{7})^2 = 9 \times 7 = 63\]
This confirms that \(3\sqrt{7}\) is indeed the correct simplified form of \(\sqrt{63}\).
Applications of the Simplified Form
The simplified radical form is useful in various mathematical contexts, such as:
- Solving Equations: Simplifying square roots makes it easier to solve algebraic equations.
- Mathematical Proofs: Using simplified forms can make mathematical proofs more elegant and understandable.
- Geometry: Simplified radicals are often used in geometric formulas and calculations involving lengths, areas, and volumes.
Examples and Practice
Understanding how to simplify square roots can be reinforced by practicing with other examples:
- \(\sqrt{72} = \sqrt{2^3 \times 3^2} = 6\sqrt{2}\)
- \(\sqrt{45} = \sqrt{3^2 \times 5} = 3\sqrt{5}\)
- \(\sqrt{98} = \sqrt{2 \times 7^2} = 7\sqrt{2}\)
By mastering the process of simplifying square roots, we gain a valuable tool for a wide range of mathematical tasks and applications.
Prime Factorization Method
The prime factorization method is a systematic approach to simplify square roots by expressing the number as a product of its prime factors. This method helps to break down the number into its simplest components, making it easier to understand and work with.
Step-by-Step Process
- Identify the Prime Factors:
The first step is to identify the prime factors of the number. For 63, we start by dividing by the smallest prime number and continue dividing until we are left with prime numbers:
\[63 \div 3 = 21\]
\[21 \div 3 = 7\]
\[7 \div 7 = 1\]
Therefore, the prime factors of 63 are:
\[63 = 3 \times 3 \times 7 = 3^2 \times 7\]
- Group the Factors:
Next, we group the prime factors in pairs where possible. For 63, we have a pair of 3s:
\[63 = (3 \times 3) \times 7 = 3^2 \times 7\]
- Simplify Using the Square Root:
We then apply the square root to each group of prime factors. The square root of \(3^2\) is 3:
\[\sqrt{63} = \sqrt{3^2 \times 7} = \sqrt{3^2} \times \sqrt{7} = 3\sqrt{7}\]
Detailed Example
To illustrate the prime factorization method, let's go through a detailed example with the number 63:
- Find the prime factors of 63:
\[63 = 3^2 \times 7\]
- Group the factors in pairs:
\[63 = (3 \times 3) \times 7 = 3^2 \times 7\]
- Simplify the square root:
\[\sqrt{63} = \sqrt{3^2 \times 7} = 3\sqrt{7}\]
Verification
To verify the simplification, we can square the simplified form and check if we get back the original number:
\[(3\sqrt{7})^2 = 3^2 \times (\sqrt{7})^2 = 9 \times 7 = 63\]
This confirms that \(3\sqrt{7}\) is indeed the correct simplified form of \(\sqrt{63}\).
Benefits of Prime Factorization Method
The prime factorization method offers several benefits:
- Accuracy: It ensures that the square root is simplified accurately.
- Clarity: It provides a clear and systematic approach to simplification.
- Applicability: It can be applied to any number, making it a versatile tool in mathematics.
Practice Examples
To practice the prime factorization method, try simplifying the square roots of the following numbers:
- \(\sqrt{72}\)
- \(\sqrt{45}\)
- \(\sqrt{98}\)
By mastering this method, you can simplify complex square roots with ease and confidence.
Applications in Mathematics
The square root of 63, denoted as √63 or \( \sqrt{63} \), has various applications in mathematics. Below are some of the key applications:
1. Solving Equations
The square root of 63 is often used in solving quadratic equations. For example, consider the equation:
\[
x^2 - 63 = 0
\]
To solve this, we add 63 to both sides and then take the square root:
\[
x^2 = 63 \implies x = \pm \sqrt{63}
\]
Thus, the solutions are:
\[
x = \pm 7.94
\]
2. Geometry
In geometry, the square root of 63 can be used to find the length of the diagonal of a square or rectangle. For instance, if a square has an area of 63 square units, the length of each side is:
\[
s = \sqrt{63} \approx 7.94 \text{ units}
\]
The diagonal \(d\) of the square is then calculated as:
\[
d = s \sqrt{2} = 7.94 \times 1.414 \approx 11.23 \text{ units}
\]
3. Trigonometry
The square root of 63 appears in trigonometric functions and identities. For example, in the context of a right triangle where one of the legs is √63, the trigonometric ratios can be calculated as follows:
If the hypotenuse \(c\) and one leg \(a\) of the right triangle are given by:
\[
a = \sqrt{63}, \quad c = 2 \sqrt{63}
\]
Then, the sine and cosine of the angle opposite the leg can be found using:
\[
\sin(\theta) = \frac{a}{c} = \frac{\sqrt{63}}{2\sqrt{63}} = \frac{1}{2}
\]
\[
\cos(\theta) = \frac{\sqrt{c^2 - a^2}}{c} = \frac{\sqrt{4 \times 63 - 63}}{2\sqrt{63}} = \frac{\sqrt{189}}{2\sqrt{63}} = \frac{\sqrt{3}}{2}
\]
4. Algebraic Simplification
The square root of 63 can be simplified in algebraic expressions to make calculations easier. For example:
\[
\sqrt{63} = \sqrt{9 \times 7} = \sqrt{9} \times \sqrt{7} = 3\sqrt{7}
\]
This simplification is useful when performing operations such as addition, subtraction, multiplication, or division with radical terms.
5. Approximation and Estimation
In many mathematical problems, it is important to approximate the square root of 63 for practical purposes. Using a calculator or estimation techniques, we find:
\[
\sqrt{63} \approx 7.94
\]
This approximation can be used in various mathematical computations where an exact value is not necessary.
In conclusion, the square root of 63 plays a crucial role in various mathematical contexts, including solving equations, geometric calculations, trigonometric functions, algebraic simplifications, and approximations.
Applications in Engineering
The square root of 63, approximately 7.937, has several applications in the field of engineering. Understanding and utilizing square roots is essential in various engineering disciplines, particularly in calculations involving geometry, structural analysis, and signal processing.
- Structural Engineering: The square root function is often used to determine dimensions and properties of structural elements. For instance, when analyzing vibrations and natural frequencies of structures, the formula for the natural frequency \( f \) of a simple harmonic oscillator involves the square root of stiffness \( k \) over mass \( m \): \[ f = \frac{1}{2\pi} \sqrt{\frac{k}{m}} \] In cases where the stiffness or mass includes factors of 63, the square root of 63 becomes directly relevant.
- Signal Processing: In signal processing, the square root is used in various algorithms to process and analyze signals. For example, the calculation of the Root Mean Square (RMS) value of a signal, which is crucial for understanding the power of electrical signals, involves taking the square root of the mean of the squares of the signal values. If a signal contains components that involve the number 63, then \(\sqrt{63}\) will be part of the RMS calculation.
- Fluid Dynamics: The square root function is used in fluid dynamics to solve for velocities and pressures in fluid flow problems. The Bernoulli equation, which relates the speed of a fluid to its pressure, often involves square roots. For example, to solve for the velocity \( v \) of fluid flow given a pressure difference, the equation: \[ v = \sqrt{\frac{2(P_1 - P_2)}{\rho}} \] If the pressure difference or density has components involving 63, the square root of 63 is used.
- Electrical Engineering: In electrical engineering, the square root of 63 might appear in calculations related to impedance in AC circuits. For example, the total impedance \( Z \) of a series RLC circuit (resistor, inductor, capacitor) is given by: \[ Z = \sqrt{R^2 + (X_L - X_C)^2} \] where \( X_L \) and \( X_C \) are the inductive and capacitive reactances respectively. If these reactances include the number 63, the square root of 63 is relevant.
- Measurement and Error Analysis: The square root function is also fundamental in error analysis and propagation. For instance, the standard deviation, which is a measure of the amount of variation or dispersion in a set of values, involves the square root of the variance. In engineering, when dealing with datasets where 63 is a significant value, the square root of 63 will be used in calculations.
Overall, the square root of 63, like other square roots, is a crucial mathematical tool in engineering, aiding in a variety of calculations that ensure the accuracy and efficiency of engineering designs and analyses.

Applications in Science
The square root of 63, approximately 7.937, finds various applications in science, ranging from physics to biology. Below are some key areas where this mathematical concept is utilized:
-
Physics:
In physics, square roots are often used to solve problems involving the Pythagorean theorem, wave functions, and energy calculations. For example, in wave mechanics, the square root function can help in determining the root-mean-square (RMS) values of alternating currents.
-
Engineering:
Engineering disciplines, such as civil and electrical engineering, use square roots to calculate forces, stresses, and other parameters critical to design and safety. For instance, calculating the load distribution on beams often involves the use of square roots.
-
Biology:
In biology, square roots can be used in statistical methods, such as calculating the standard deviation in population studies or growth rates. This helps in understanding variations and patterns within biological data.
-
Environmental Science:
Environmental scientists use square roots in various modeling equations to predict pollution levels, resource consumption, and sustainability metrics. For example, diffusion models in environmental studies often involve square root calculations.
-
Chemistry:
Chemists use square roots in equations such as the calculation of reaction rates and equilibrium constants. This is essential for understanding how reactions progress over time and under different conditions.
The utility of the square root of 63 extends across numerous scientific fields, underpinning many theoretical and practical applications that require precise and accurate mathematical calculations.
Graphical Representation of the Square Root of 63
The square root of 63, denoted as \(\sqrt{63}\), is approximately 7.937. To graphically represent this value, we can visualize it on a number line and within the context of a Cartesian plane.
Number Line Representation
On a number line, \(\sqrt{63}\) lies between 7 and 8, closer to 8. This can be shown as:
Cartesian Plane Representation
In a Cartesian plane, we can represent \(\sqrt{63}\) by plotting the point (7.937, 0) along the x-axis. Additionally, to show the square root function graphically, we can plot the function \(y = \sqrt{x}\) and highlight the point where \(x = 63\).
The function \(y = \sqrt{x}\) is a curve that increases gradually and flattens out as \(x\) increases. Here is a simplified table of values and the corresponding graph:
| \(x\) | \(y = \sqrt{x}\) |
|---|---|
| 49 | 7.0 |
| 63 | 7.937 |
| 64 | 8.0 |
| 81 | 9.0 |
Detailed Steps for Graphical Representation
- Plot the square root function \(y = \sqrt{x}\) on a graph.
- Identify the point where \(x = 63\).
- Determine the corresponding \(y\)-value, which is \(y = 7.937\).
- Highlight or mark the point \((63, 7.937)\) on the graph.
This graphical approach helps in understanding the position and value of \(\sqrt{63}\) within the broader context of square roots and their properties.
Approximation Techniques
The square root of 63 can be approximated using several methods. Here are some of the common techniques:
-
Long Division Method
The long division method provides a systematic way to approximate square roots to a desired degree of accuracy. This method is similar to the long division process used for dividing numbers, but it involves additional steps to handle the square root calculation.
- Start by pairing the digits of the number from right to left.
- Find the largest number whose square is less than or equal to the leftmost pair or single digit.
- Subtract the square of this number from the leftmost pair or single digit and bring down the next pair of digits.
- Double the number found in step 2 and use it as a trial divisor.
- Find a digit which, when added to the trial divisor and multiplied by the result, is less than or equal to the current dividend.
- Repeat the process until the desired precision is achieved.
-
Prime Factorization
This method is useful for simplifying square roots of perfect squares, but it can also aid in approximations for non-perfect squares.
For the square root of 63:
- Prime factorize 63: \( 63 = 3^2 \times 7 \)
- Express the square root using the prime factors: \( \sqrt{63} = \sqrt{3^2 \times 7} = 3\sqrt{7} \)
- Approximate \( \sqrt{7} \approx 2.6457513110645906 \), thus \( 3\sqrt{7} \approx 3 \times 2.6457513110645906 = 7.937253933 \)
-
Newton's Method (Heron's Method)
Newton's Method is an iterative approach to find increasingly accurate approximations of square roots.
- Start with an initial guess \( x_0 \). A reasonable guess for \( \sqrt{63} \) might be 8.
- Use the formula \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{63}{x_n} \right) \)
- Repeat the process until the difference between \( x_n \) and \( x_{n+1} \) is less than the desired precision.
-
Using a Calculator
For quick approximations, using a calculator is the most straightforward method. Simply input the number 63 and use the square root function to get the result \( \sqrt{63} \approx 7.937 \).
By employing these methods, the square root of 63 can be approximated with a high degree of accuracy, suitable for various mathematical and practical applications.
Comparison with Other Square Roots
The square root of 63, approximately 7.937, provides an interesting comparison with other square roots. This comparison can be beneficial in understanding its relative value and applications.
Here are some comparisons with other square roots:
- Square Root of 49 (√49 = 7): The square root of 49 is exactly 7. Since 49 is a perfect square, its square root is an integer. This contrasts with the square root of 63, which is not a perfect square and hence an irrational number.
- Square Root of 64 (√64 = 8): The square root of 64 is exactly 8. 64 is another perfect square, making its square root a whole number. The square root of 63 falls between the square roots of 49 and 64, highlighting its non-integer nature.
- Square Root of 62 (√62 ≈ 7.874): The square root of 62 is approximately 7.874. Comparing this with the square root of 63 shows that even though they are close in value, both are irrational numbers and are not perfect squares.
- Square Root of 81 (√81 = 9): The square root of 81 is exactly 9, a higher perfect square. The significant difference between 63 and 81 underscores the leap in value between non-perfect and perfect squares.
To visualize these comparisons, consider a number line:

From this comparison, it becomes clear that the square root of 63, while close to the square roots of neighboring perfect squares, stands out as an irrational number with a non-terminating, non-repeating decimal expansion.
This understanding is crucial in various mathematical contexts, including algebra and geometry, where approximations and exact values play significant roles in problem-solving and proofs.

Common Misconceptions
The square root of 63, like many mathematical concepts, is often subject to various misconceptions. Understanding these misconceptions helps in gaining a clearer and more accurate perspective on the topic.
-
Misconception 1: The square root has two values (+ and -)
One common misconception is that the square root of a number has two values: a positive and a negative. While it is true that solving the equation \(x^2 = 63\) yields two solutions (\(x = \pm \sqrt{63}\)), the square root function itself, by definition, returns only the principal (positive) root. Thus, \(\sqrt{63}\) is approximately 7.937, not \(\pm 7.937\).
-
Misconception 2: Square roots of non-perfect squares are rational
Another misconception is that the square roots of all numbers are rational. However, the square root of 63 is an irrational number because it cannot be expressed as a fraction of two integers. It is a non-terminating and non-repeating decimal.
-
Misconception 3: Estimation is not accurate
Many believe that estimating the square root of a number cannot yield an accurate result. While it's true that approximations are not exact, techniques such as long division and iterative methods can provide highly precise values. For instance, \(\sqrt{63} \approx 7.937\), which is quite accurate for most practical purposes.
Understanding these misconceptions is crucial for a proper grasp of the mathematical concepts surrounding square roots. Correcting these misunderstandings allows for a deeper appreciation and more accurate application of mathematical principles.
Frequently Asked Questions
-
What is the square root of 63?
The square root of 63 is approximately 7.94, which can also be expressed in its simplified radical form as \(3\sqrt{7}\).
-
Is the square root of 63 a rational number?
No, the square root of 63 is an irrational number because it cannot be expressed as a fraction of two integers.
-
How do you simplify the square root of 63?
To simplify the square root of 63, you factor it into its prime factors: \(63 = 3^2 \times 7\). Thus, \(\sqrt{63} = \sqrt{3^2 \times 7} = 3\sqrt{7}\).
-
What is the decimal representation of the square root of 63?
The decimal representation of the square root of 63 is approximately 7.93725.
-
How is the square root of 63 used in real life?
The square root of 63 is used in various mathematical and scientific applications, such as in solving quadratic equations, engineering calculations, and in geometric measurements.
Conclusion
The square root of 63, approximately 7.937, is a non-terminating and non-repeating decimal, classifying it as an irrational number. Throughout this guide, we have explored various aspects of the square root of 63, including its mathematical properties, applications in different fields, and methods of approximation.
In mathematics, the square root of 63 plays a crucial role in algebra and geometry, particularly in solving quadratic equations and understanding geometric shapes. Engineering applications often leverage this value in design calculations and optimization problems, while in science, it aids in statistical analysis and physical measurements.
We have also visualized the square root of 63 graphically, helping to grasp its significance on the number line. Approximation techniques such as the long division method and iterative algorithms were discussed to provide accurate values when needed.
Understanding the square root of 63 in comparison to other square roots revealed interesting insights into its relative magnitude and properties. Common misconceptions, such as confusing it with a rational number or misinterpreting its exact form, were clarified.
By addressing frequently asked questions, we aimed to provide a comprehensive understanding of the square root of 63, reinforcing the importance of precision and clarity in mathematical discussions.
In conclusion, the square root of 63 is more than just a number; it is a fundamental concept with diverse applications and significant implications across various disciplines. By mastering its properties and uses, one gains a deeper appreciation of the interconnectedness of mathematical principles and their practical applications.
Khám phá cách tính và ứng dụng của căn bậc hai của 63 trong toán học, kỹ thuật và khoa học.
Căn bậc hai của 63