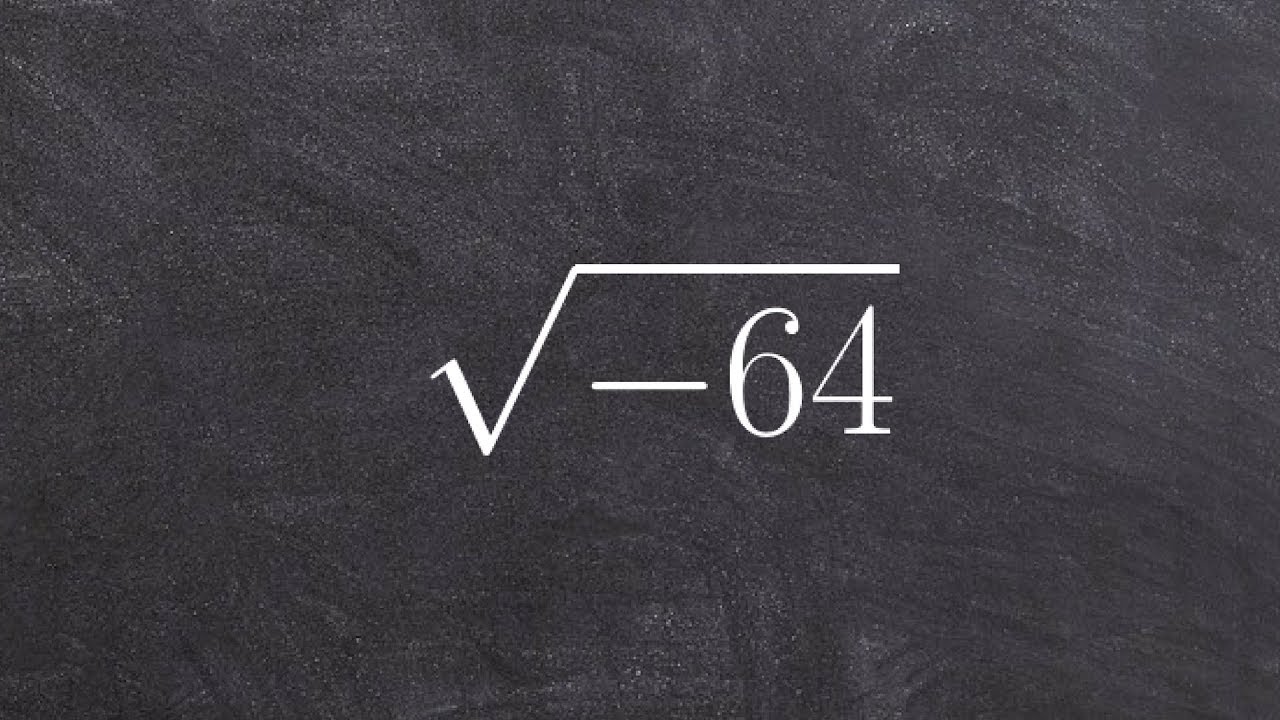Topic what is a square root of 64: Ever wondered what is a square root of 64? This article dives into the concept, providing a clear explanation, properties, and real-life applications. Whether you're a student or just curious, you'll find valuable insights and practical examples that make understanding the square root of 64 both easy and fascinating.
Table of Content
- Understanding the Square Root of 64
- Introduction
- Understanding Square Roots
- What is a Square Root?
- Definition of the Square Root of 64
- How to Calculate the Square Root of 64
- Mathematical Explanation
- Positive and Negative Roots
- Applications of the Square Root of 64
- Real-Life Examples
- Square Roots in Geometry
- Square Roots in Physics
- Square Roots in Engineering
- Common Misconceptions about Square Roots
- Historical Context of Square Roots
- Conclusion
- YOUTUBE:
Understanding the Square Root of 64
The concept of the square root is fundamental in mathematics, providing a basis for various calculations and problem-solving techniques.
Definition of Square Root
The square root of a number is a value that, when multiplied by itself, gives the original number. Mathematically, if \( x^2 = a \), then \( x \) is the square root of \( a \).
Calculation of the Square Root of 64
To find the square root of 64, we seek a number that, when squared, equals 64. In other words, we are looking for \( x \) such that:
\[
x^2 = 64
\]
By solving this equation, we find:
\[
x = \pm \sqrt{64}
\]
Since 8 multiplied by 8 gives 64, we have:
\[
\sqrt{64} = 8
\]
Thus, the principal (positive) square root of 64 is 8. However, considering both positive and negative roots, we have:
\[
\pm \sqrt{64} = \pm 8
\]
Properties of the Square Root of 64
- 64 is a perfect square because its square root is an integer.
- The square roots of 64 are both positive 8 and negative 8.
- It is a rational number.
Applications of Square Roots
Understanding square roots is essential for various real-life applications, such as:
- Geometry: Calculating the length of sides in right-angled triangles.
- Physics: Determining wave frequencies and other measurements.
- Engineering: Solving problems related to structural design and stability.
Summary
The square root of 64 is an essential concept that showcases the elegance and utility of mathematical principles. Embracing such knowledge empowers us to solve complex problems and appreciate the underlying structure of the world around us.

READ MORE:
Introduction
The square root of a number is a value that, when multiplied by itself, gives the original number. The square root of 64 is one of the most commonly asked questions in mathematics. In this section, we will explore what a square root is, how to calculate it, and why it's important.
The square root of 64 is 8 because 8 multiplied by itself (8 × 8) equals 64. This can be expressed as:
\[\sqrt{64} = 8\]
Additionally, -8 is also a square root of 64 because (-8) × (-8) equals 64. Thus:
\[\sqrt{64} = \pm8\]
Here are the key points about the square root of 64:
- The principal (positive) square root of 64 is 8.
- The negative square root of 64 is -8.
- Square roots are essential in various mathematical applications, including geometry and algebra.
Understanding square roots helps in solving quadratic equations, working with exponents, and in real-life applications such as physics and engineering. In the following sections, we will dive deeper into methods to calculate square roots and their properties.
Understanding Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 64 is 8 because \(8 \times 8 = 64\). This concept is fundamental in mathematics and has various applications in different fields.
Let's explore the properties and methods to calculate square roots:
- Definition: The square root of a number \(n\) is denoted as \(\sqrt{n}\) or \(n^{1/2}\). For 64, it is written as \(\sqrt{64} = 8\).
- Perfect Squares: A perfect square is a number that has an integer as its square root. Since \(8 \times 8 = 64\), 64 is a perfect square.
- Rational or Irrational: If the square root of a number is an integer, it is a rational number. Since \(\sqrt{64} = 8\), it is rational.
- Calculation Methods:
- Using a Calculator: Most calculators have a square root function. Simply enter 64 and press the square root button to get 8.
- Prime Factorization: Break down 64 into prime factors: \(64 = 2^6\). Taking the square root of each factor, \(\sqrt{64} = 2^3 = 8\).
- Long Division: A manual method where you pair digits from the right and estimate the square root digit by digit. This method is useful for non-perfect squares.
- Applications: Square roots are used in geometry to find the side lengths of squares and in various formulas in physics, engineering, and statistics.
Understanding square roots helps in solving equations and understanding the properties of numbers, making it a crucial concept in mathematics.
What is a Square Root?
The square root of a number is a value that, when multiplied by itself, results in the original number. Mathematically, if \( p \) is the square root of \( q \), then \( p = \sqrt{q} \) or \( p^2 = q \). For example, \( \sqrt{64} = 8 \) because \( 8 \times 8 = 64 \). The symbol used to represent the square root is the radical sign (√).
There are two square roots for every positive number: one positive and one negative. Thus, the square roots of 64 are +8 and -8.
To find the square root of a number, several methods can be used, including:
- Prime factorization method
- Long division method
- Repeated subtraction method
Each of these methods provides a systematic way to determine the square root of a given number.
Definition of the Square Root of 64
The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 64 is 8 because \( 8 \times 8 = 64 \). This means that the square root of 64 is 8.
To calculate the square root of 64, we can use several methods:
- Manual Calculation: Find a number that when squared (multiplied by itself) results in 64. In this case, \( 8 \times 8 = 64 \), so the square root of 64 is 8.
- Using a Calculator: Enter 64 and press the square root (√) button to get the result of 8.
- Using Excel or Google Sheets: Use the formula
=SQRT(64)to get the result of 8.
Additionally, it's important to understand the concept of principal and negative square roots. Every positive number has two square roots: one positive and one negative. Therefore, the square roots of 64 are +8 and -8. However, by convention, when we refer to the square root of a number, we usually mean the positive or principal square root. In this case, it is +8.
The square root of 64 is also classified as a rational number because it can be expressed as a fraction of two integers. Since 8 is a whole number, it confirms that 64 is a perfect square, and its square root is rational.
| Root | Expression | Value |
|---|---|---|
| Square Root | \(\sqrt{64}\) | 8.000 |
| Cube Root | \(\sqrt[3]{64}\) | 4.000 |
| Fourth Root | \(\sqrt[4]{64}\) | 2.828 |
| Fifth Root | \(\sqrt[5]{64}\) | 2.297 |
| Sixth Root | \(\sqrt[6]{64}\) | 2.000 |
| Seventh Root | \(\sqrt[7]{64}\) | 1.811 |
| Eighth Root | \(\sqrt[8]{64}\) | 1.682 |
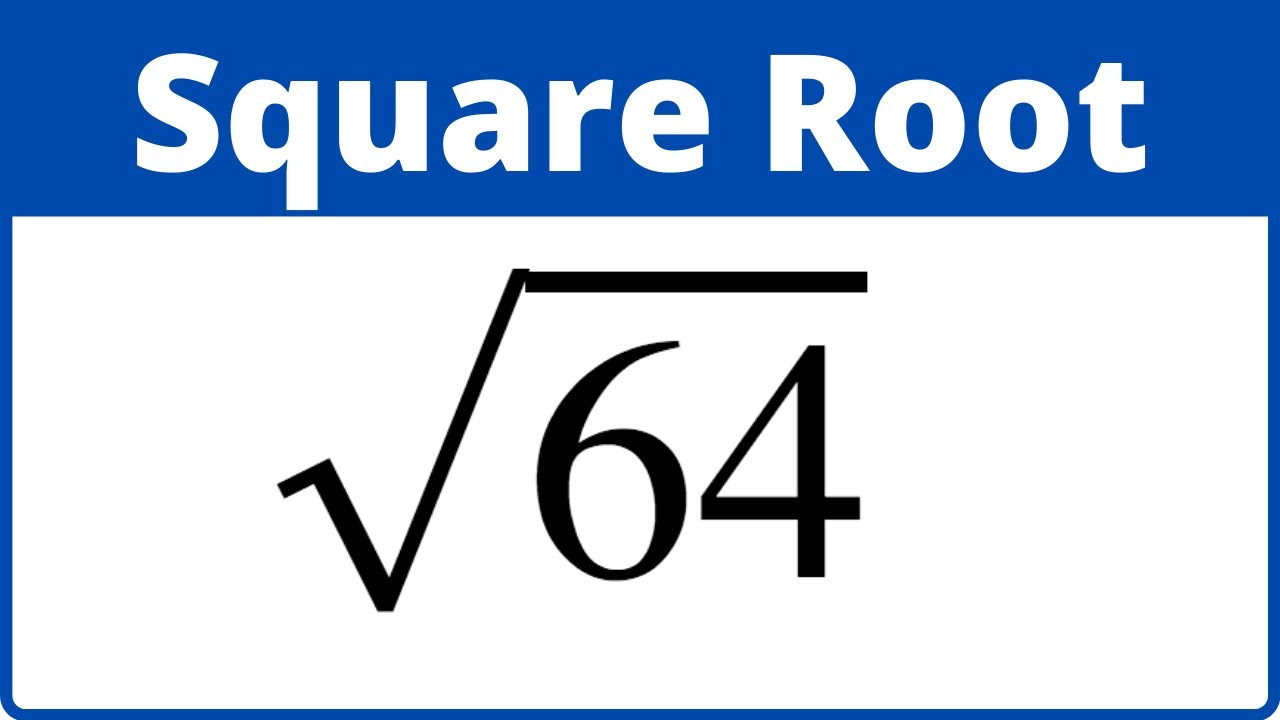
How to Calculate the Square Root of 64
Calculating the square root of 64 can be done using several methods. Here are the most common ones explained in detail:
- Repeated Subtraction Method: In this method, we subtract successive odd numbers from 64 until we reach zero. The number of subtractions gives the square root.
- 64 - 1 = 63
- 63 - 3 = 60
- 60 - 5 = 55
- 55 - 7 = 48
- 48 - 9 = 39
- 39 - 11 = 28
- 28 - 13 = 15
- 15 - 15 = 0
We subtract 8 times to get zero, so the square root of 64 is 8.
- Prime Factorization Method: This method involves expressing 64 as a product of prime factors.
- 64 = 2 × 2 × 2 × 2 × 2 × 2
- Group the factors into pairs: (2 × 2) × (2 × 2) × (2 × 2) = 8
So, the square root of 64 is 8.
- Long Division Method: This method is used for finding the square root of both perfect squares and non-perfect squares.
- Pair the digits from right to left: 64
- Find a number which square is less than or equal to 64: 8 × 8 = 64
- The quotient is the square root: 8
Thus, the square root of 64 is 8.
Each method demonstrates that the square root of 64 is indeed 8, reaffirming the consistency of mathematical principles.
Mathematical Explanation
The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 64 is 8, because \(8 \times 8 = 64\). This section delves into the mathematical reasoning behind this calculation and its implications.
Mathematically, the square root of a number \(x\) is denoted as \(\sqrt{x}\). For positive numbers, the square root function yields the principal (positive) root. Thus:
- \(\sqrt{64} = 8\)
To calculate the square root of 64 manually, you can use the following steps:
- Recognize that you need to find a number that, when multiplied by itself, equals 64.
- List perfect squares close to 64, such as \(1, 4, 9, 16, 25, 36, 49, 64\).
- Identify that \(64 = 8^2\), so \(\sqrt{64} = 8\).
This calculation can also be performed using tools like calculators, Excel, or Google Sheets. For instance, in Excel, you can use the formula:
SQRT(64)
This will automatically display the square root of 64 as 8.
It's important to note that the square root function only provides the principal square root. While both \(8\) and \(-8\) satisfy the equation \(x^2 = 64\), by definition, the square root function \(\sqrt{x}\) returns the non-negative root. Hence:
- \(\sqrt{64} \ne \pm 8\)
The square root function has several important properties:
- For any non-negative number \(x\), \(\sqrt{x}\) is defined and non-negative.
- The function \(\sqrt{x}\) is continuous for \(x \geq 0\).
- If \(x\) is a perfect square, \(\sqrt{x}\) is an integer.
Understanding these properties helps in various mathematical applications and problem-solving scenarios. For example, knowing that the square root of 64 is 8 allows for quick verification in algebraic expressions and equations.
Positive and Negative Roots
When considering the square root of a number, it is essential to understand that every positive real number has two square roots: one positive and one negative. This is because both positive and negative numbers, when squared, result in a positive number.
For the number 64, the square roots are:
- Positive square root:
\(\sqrt{64} = 8\) - Negative square root:
\(\sqrt{64} = -8\)
Here's a detailed explanation:
Positive Square Root: The positive square root of 64 is 8 because 8 multiplied by itself equals 64.
\[ 8 \times 8 = 64 \] Negative Square Root: The negative square root of 64 is -8 because -8 multiplied by itself also equals 64.
\[ -8 \times -8 = 64 \]
It is important to note the distinction between the principal square root and the general concept of square roots:
- The principal square root refers to the non-negative square root of a number. For 64, the principal square root is 8.
- The negative square root is the negative counterpart, which is -8 in the case of 64.
In mathematical notation, we can represent the positive and negative square roots of 64 as follows:
This notation indicates both the positive and negative roots simultaneously.
Understanding both roots is crucial in various mathematical contexts, including solving quadratic equations, where both positive and negative solutions might be relevant depending on the problem's context.
Applications of the Square Root of 64
The square root of 64, which is 8, has various practical applications in different fields. Here are some key areas where it is used:
1. Geometry
In geometry, the square root of 64 can be used to determine the dimensions of squares and rectangles. For example:
- If the area of a square is 64 square units, then the length of each side is the square root of 64, which is 8 units.
- It helps in calculating the diagonal of a square. Given a square with side length 8, the diagonal \( d \) can be calculated using the Pythagorean theorem: \( d = \sqrt{8^2 + 8^2} = \sqrt{128} = 8\sqrt{2} \).
2. Physics
In physics, the square root of 64 is used in various calculations involving area, energy, and other physical properties:
- Calculating the side length of a square-shaped surface with an area of 64 square units, which is often useful in experiments and theoretical models.
- Determining the amplitude of waves or vibrations if the squared value represents the energy or intensity. For instance, if the energy of a wave is proportional to 64 units, the amplitude would be 8 units.
3. Engineering
In engineering, the square root of 64 is applied in structural design and analysis:
- Designing components where the area is crucial, such as plates and beams. For example, a square plate with an area of 64 square inches would have sides of 8 inches each.
- Calculating the moment of inertia for square cross-sections, which is important in determining the stress and strain on materials.
4. Real-Life Examples
There are many real-life examples where the square root of 64 is applicable:
- In architecture, determining the dimensions of square tiles or flooring. A tile with an area of 64 square inches will have sides of 8 inches.
- In land measurement, calculating the side length of a square plot with an area of 64 square meters.
- In sports, such as creating square playing fields or courts where each side is 8 units long if the total area is 64 square units.
5. Computer Science
In computer science, the square root of 64 can be relevant in algorithms and data structure designs:
- Optimizing data storage and retrieval where squared values are used, such as in hash tables or memory allocation.
- Using square roots in graphics and game development to calculate distances and proportions accurately.

Real-Life Examples
The square root of 64, which is 8, has several practical applications in real-life scenarios. Here are a few examples:
- Geometry: If you have a square with an area of 64 square units, each side of the square will be the square root of 64. Hence, each side will be 8 units long. This is crucial in design and architecture where precise measurements are needed.
- Construction: When constructing square tiles or plots of land, knowing the square root helps in determining the side length. For a square plot of land with an area of 64 square meters, each side will measure 8 meters.
- Physics: In physics, the square root function is often used to determine quantities like the magnitude of vectors. For instance, if the squared displacement in a particular direction is 64 units, the actual displacement is the square root of 64, which is 8 units.
- Engineering: Engineers frequently use square roots in various calculations. For example, if a component has a design tolerance area of 64 square millimeters, the length of each side of the component will be 8 millimeters.
- Computer Graphics: In computer graphics, when creating textures or images with equal dimensions (e.g., 64x64 pixels), the square root is used to ensure uniform scaling and resolution.
- Finance: In finance, the square root can be used in risk management and portfolio optimization. For example, if a variance (a measure of risk) is 64, the standard deviation (another measure of risk) will be 8, which is the square root of 64.
- Sports: In sports, especially in track and field events, knowing the square root is useful for calculating distances. For instance, if an athlete's running track forms a perfect square with an area of 64 square meters, the length of each side of the track will be 8 meters.
These examples illustrate how the concept of the square root of 64, being 8, is utilized across various fields and everyday situations, showcasing its practical importance.
Square Roots in Geometry
Square roots play a crucial role in various geometric calculations and constructions. Here are some examples:
1. Area of Squares
The square root is directly used to find the side length of a square when its area is known. For instance, if the area of a square is 64 square units, the length of each side is the square root of 64, which is 8 units.
\[
\text{Side length} = \sqrt{\text{Area}} = \sqrt{64} = 8
\]
2. Diagonal of a Square
In a square, the diagonal can be found using the square root. The relationship between the side length \(a\) and the diagonal \(d\) is given by:
\[
d = a\sqrt{2}
\]
For a square with a side length of 8 units, the diagonal is:
\[
d = 8\sqrt{2} \approx 11.31 \text{ units}
\]
3. Distance Formula
In coordinate geometry, the distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) is calculated using the square root of the sum of the squares of the differences in x and y coordinates:
\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]
4. Pythagorean Theorem
The Pythagorean theorem states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. If the lengths of the legs are 8 units each, the length of the hypotenuse \(c\) is:
\[
c = \sqrt{8^2 + 8^2} = \sqrt{64 + 64} = \sqrt{128} = 8\sqrt{2} \approx 11.31 \text{ units}
\]
5. Circle Geometry
To find the radius of a circle when the area is known, we use the square root. If the area \(A\) is given by \(A = \pi r^2\), for a circle with area \(64\pi\) square units, the radius \(r\) is:
\[
64\pi = \pi r^2 \implies r^2 = 64 \implies r = \sqrt{64} = 8 \text{ units}
\]
6. Constructing Squares
In geometric constructions, square roots are used to construct squares of a given area using a compass and straightedge. Knowing the square root of the area helps in setting the correct side lengths during construction.
These examples highlight the importance and versatility of square roots in geometry, demonstrating their application in various fundamental concepts and calculations.
Square Roots in Physics
The concept of square roots plays a significant role in various areas of physics, helping to solve equations and understand relationships between different physical quantities. Here are some detailed applications of square roots in physics:
-
Kinematics:
In kinematics, the equation for the velocity (\(v\)) of an object under constant acceleration (\(a\)) over a distance (\(d\)) can be expressed as:
\[
v = \sqrt{2ad}
\]
This equation shows that the velocity is proportional to the square root of the product of acceleration and distance. -
Energy:
The kinetic energy (\(KE\)) of a moving object is given by the formula:
\[
KE = \frac{1}{2}mv^2
\]
To find the velocity when the kinetic energy and mass (\(m\)) are known, we rearrange the formula:
\[
v = \sqrt{\frac{2KE}{m}}
\] -
Wave Speed:
The speed of a wave on a string (\(v\)) is determined by the tension (\(T\)) in the string and the linear mass density (\(\mu\)):
\[
v = \sqrt{\frac{T}{\mu}}
\]
Here, the speed is directly proportional to the square root of the tension divided by the mass per unit length of the string. -
Gravitational Potential Energy:
In astrophysics, the escape velocity (\(v_{e}\)) from a planet is derived from the gravitational potential energy equation. It is given by:
\[
v_{e} = \sqrt{\frac{2GM}{R}}
\]
where \(G\) is the gravitational constant, \(M\) is the mass of the planet, and \(R\) is the radius from the center of the planet to the point of escape. -
Quantum Mechanics:
In quantum mechanics, the Heisenberg uncertainty principle involves the standard deviation (\(\sigma\)) of position and momentum:
\[
\sigma_x \sigma_p \geq \frac{\hbar}{2}
\]
Here, the calculation of standard deviation often involves square roots to quantify the uncertainties.
Square Roots in Engineering
The concept of square roots, particularly the square root of 64, plays a significant role in various engineering fields. Here are some applications and examples of how square roots are utilized in engineering:
-
Structural Engineering:
In structural engineering, the square root of 64 (which is 8) can be used in calculations related to material properties and load distribution. For instance, when determining the natural frequencies of structures, the square root of specific constants and ratios is often required to find resonance frequencies.
-
Electrical Engineering:
In electrical engineering, square roots are essential in AC circuit analysis. The square root of the sum of squares of the resistive and reactive components, known as impedance, is used to determine the overall opposition to current flow in the circuit.
-
Mechanical Engineering:
In mechanical engineering, the square root of 64 can be applied in calculating stress and strain in materials. For example, the formula for the critical buckling load of a column involves the square root of the moment of inertia and other factors, ensuring the structure can withstand specific loads without collapsing.
-
Civil Engineering:
Civil engineers often use square roots in surveying and construction to calculate distances, slopes, and elevations. The Pythagorean theorem, which involves square roots, is frequently employed to ensure accuracy in the design and layout of infrastructure projects.
-
Thermodynamics and Heat Transfer:
In thermodynamics, the square root of values related to thermal conductivity and diffusivity can determine the rate at which heat is transferred through materials. Engineers use these calculations to design efficient thermal systems and manage energy consumption.
-
Fluid Dynamics:
In fluid dynamics, the square root of parameters such as Reynolds number and Froude number helps engineers predict the behavior of fluid flow, including turbulence and wave formation. These calculations are crucial for designing pipelines, water treatment systems, and aerodynamic structures.
The square root of 64 is just one example, but its applications across different engineering disciplines demonstrate the importance of understanding and utilizing square roots in complex calculations and problem-solving.

Common Misconceptions about Square Roots
Square roots are often misunderstood in various ways. Here are some common misconceptions:
-
Square Root Always Has Two Values:
One of the most prevalent misconceptions is that the square root of a number always has two values. While it is true that the equation \( x^2 = 64 \) has two solutions (\( x = 8 \) and \( x = -8 \)), the principal square root function, denoted as \( \sqrt{64} \), is defined to be the non-negative value, which is 8.
-
Square Root and Squaring are Perfect Inverses:
Another common error is assuming that taking the square root and squaring are always perfect inverses. This is true for non-negative numbers, but for negative numbers, the square root function is not defined within the real numbers. For example, \( \sqrt{x^2} \) simplifies to \( |x| \), not \( x \).
-
Distributing Square Roots Over Addition:
Some students incorrectly believe that square roots can be distributed over addition, such as thinking \( \sqrt{a^2 + b^2} = \sqrt{a^2} + \sqrt{b^2} = a + b \). This is incorrect. The correct interpretation is that \( \sqrt{a^2 + b^2} \) cannot be simplified in this way.
-
Misinterpreting the Domain and Range of Square Roots:
There is often confusion about the domain (input values) and range (output values) of the square root function. The square root function \( \sqrt{x} \) is only defined for non-negative values of \( x \) within the real numbers, and its range is also non-negative. For example, \( \sqrt{-64} \) is not defined in the real numbers, but in the complex number system, it equals \( 8i \).
-
Incorrectly Applying Square Root to Negative Numbers:
Many believe that the square root of a negative number is undefined, which is true in the real number system. However, in the complex number system, the square root of a negative number is defined and involves imaginary numbers. For instance, \( \sqrt{-64} = 8i \), where \( i \) is the imaginary unit.
Historical Context of Square Roots
The concept of square roots has a rich history that dates back to ancient civilizations. The earliest known records of square roots come from the ancient Babylonians, who used geometric methods to approximate square roots as early as 1900 BCE. They developed a number system based on 60 (sexagesimal), which allowed for relatively accurate calculations of square roots.
In ancient Egypt, around 1650 BCE, the Rhind Mathematical Papyrus contains problems that involve square roots, demonstrating the Egyptians' understanding of these concepts in practical contexts like construction and land measurement.
Ancient Indian mathematicians made significant contributions to the understanding of square roots. The Sulba Sutras (800-500 BCE) provided rules for calculating square roots, particularly in the context of constructing sacrificial altars. Aryabhata, an Indian mathematician from the 5th century, developed methods for finding square roots and used them in his astronomical calculations.
The Greek mathematician Euclid, in his work "Elements" (circa 300 BCE), provided a geometric interpretation of square roots. He used the Pythagorean Theorem to demonstrate how to find the square root of a number, a method still taught in geometry classes today. Another Greek mathematician, Archimedes, made advancements in understanding the properties of square roots and their applications in various geometric problems.
During the Islamic Golden Age, mathematicians like Al-Khwarizmi and Al-Haytham (Alhazen) further refined methods for extracting square roots. Al-Khwarizmi's work on algebra included algorithms for finding square roots, while Alhazen applied these concepts in optics and geometry.
In the European Middle Ages and Renaissance, mathematicians continued to build on the knowledge of square roots. Fibonacci, in his book "Liber Abaci" (1202), introduced the square root symbol and detailed methods for calculating square roots using Arabic numerals.
By the 17th century, mathematicians such as René Descartes and Isaac Newton developed more sophisticated techniques for finding square roots. Descartes' work in analytical geometry and Newton's method of successive approximations (now known as the Newton-Raphson method) provided more efficient ways to calculate square roots, paving the way for modern computational methods.
Today, the square root of 64, which is 8, is commonly used in various fields of science and engineering. The historical development of square roots showcases the collaboration and cumulative knowledge of various civilizations, leading to the advanced mathematical techniques we use today.
Conclusion
The square root of 64 is a fundamental concept in mathematics with wide-ranging applications across various fields. Understanding that the square root of 64 is 8 allows us to see its utility in solving mathematical problems, engineering tasks, and physical computations.
In mathematics, the concept of square roots is essential for simplifying equations and understanding properties of numbers. The square root of 64, specifically, demonstrates how perfect squares are derived and used in algebraic expressions and problem-solving.
In physics, square roots play a crucial role in formulas involving areas and volumes, such as calculating the distance or understanding the inverse-square laws. The simplicity of the square root of 64 helps illustrate these physical laws in educational settings.
Within engineering, the knowledge of square roots, including the square root of 64, is applied in designing structures, analyzing forces, and optimizing systems. Engineers frequently use square roots in calculations to ensure precision and accuracy in their projects.
Furthermore, the understanding of square roots extends to everyday applications, such as estimating dimensions, performing financial calculations, and even in technology development where algorithm efficiency can be optimized.
In conclusion, the square root of 64 is not just a number but a gateway to comprehending deeper mathematical principles and their applications in real-world scenarios. Its value, 8, simplifies complex calculations and enhances our ability to solve problems across multiple disciplines.
Căn Bậc Hai của 64
READ MORE:
Cách Tính Căn Bậc Hai của 64: Sqrt(64)