What is the Positive Square Root of 64? Discover the Answer!

The square root of a number is a value that, when multiplied by itself, gives the original number. For the number 64, its square root can be found by determining what number, when squared, equals 64.

Calculation

The calculation to determine the square root of 64 is:

√64 = 8

Explanation

Here’s a step-by-step explanation:

1. The square root of a number x is a number y such that y² = x.
2. For the number 64, we need to find a number y such that y² = 64.
3. By testing numbers or using a calculator, we find that 8 × 8 = 64.
4. Thus, the positive square root of 64 is 8.

Properties of Square Roots

Some important properties of square roots include:

• Non-negative: The principal square root of a non-negative number is non-negative.
• Unique positive root: Each positive number has one unique positive square root.

Applications

Knowing the square root of 64 can be useful in various applications such as:

• Geometry: Finding the side length of a square with an area of 64 square units.
• Algebra: Solving quadratic equations where 64 is a constant term.

Square roots are fundamental mathematical concepts that are essential in various fields of study. The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 64 is a number which, when squared, equals 64.

Understanding square roots involves the following key points:

• Definition: The square root of a number x is a number y such that y² = x.
• Positive and Negative Roots: Every positive number has two square roots: one positive and one negative. However, the principal square root is the non-negative root. For 64, the positive square root is 8, as \(8 \times 8 = 64\).
• Perfect Squares: Numbers like 64, which are the squares of integers, are known as perfect squares. Their square roots are whole numbers.
• Notation: The square root is denoted by the radical symbol (√). For example, the square root of 64 is written as √64.

To find the square root of a number, you can use several methods:

1. Prime Factorization: Break down the number into its prime factors and pair them to find the square root.
2. Estimation: Use the closest perfect squares to estimate the square root.
3. Calculator: Use a calculator for quick and accurate results.

Square roots have important applications in geometry, algebra, and various real-world scenarios. They are used to determine the side lengths of squares, solve quadratic equations, and in many other mathematical contexts.

The square root of a number is a value that, when multiplied by itself, yields the original number. Mathematically, if y is the square root of x, then:

\( y^2 = x \)

This can also be expressed as:

\( y = \sqrt{x} \)

For example, the positive square root of 64 is 8, since:

\( 8 \times 8 = 64 \)

or

\( 8^2 = 64 \)

Key points about square roots include:

• Principal Square Root: The principal square root of a non-negative number is its non-negative square root. For instance, the principal square root of 64 is 8.
• Two Roots: Every positive number has two square roots: one positive and one negative. However, the term "square root" usually refers to the principal (positive) square root.
• Notation: The square root is represented by the radical symbol (√). For example, the square root of 64 is denoted as √64.

To summarize, the square root of a number x is a number y such that y multiplied by itself equals x. The positive square root is used most often in practical applications and mathematical contexts.

To find the square root of 64, we need to determine a number which, when multiplied by itself, equals 64. This process can be understood through several methods:

1. Prime Factorization Method:
   • First, factorize 64 into its prime factors: \( 64 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 = 2^6 \).
   • Pair the prime factors: \( (2 \times 2) \times (2 \times 2) \times (2 \times 2) \).
   • Take one number from each pair: \( 2 \times 2 \times 2 = 8 \).
   • Thus, the square root of 64 is \( 8 \).
2. Estimation Method:
   • Find two perfect squares between which 64 lies. These are \( 49 \) (since \( 7^2 = 49 \)) and \( 81 \) (since \( 9^2 = 81 \)).
   • Estimate that the square root of 64 is closer to 8 because \( 64 \) is exactly \( 8 \times 8 \).
3. Using a Calculator:
   • Enter the number 64 into the calculator and use the square root function (√) to find the result.
   • The calculator will show that the square root of 64 is 8.

Let's verify the result using basic multiplication:

\( 8 \times 8 = 64 \)

\( 8^2 = 64 \)

Therefore, the positive square root of 64 is indeed \( 8 \). This calculation is fundamental in understanding square roots and their properties.

Finding the positive square root of 64 involves a straightforward mathematical process. Here’s a detailed, step-by-step guide to help you understand how to calculate it:

1. Understand the Problem:

   We need to find a number that, when multiplied by itself, gives 64. Mathematically, this is finding \( y \) such that \( y^2 = 64 \).

2. Prime Factorization Method:
   1. Start with the number 64.
   2. Factorize 64 into its prime factors: \( 64 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \).
   3. Express 64 as a power of 2: \( 64 = 2^6 \).
   4. Pair the factors: \( (2 \times 2) \times (2 \times 2) \times (2 \times 2) \).
   5. Take one number from each pair: \( 2 \times 2 \times 2 = 8 \).
   6. Thus, the square root of 64 is \( 8 \).
3. Estimation Method:
   1. Identify two perfect squares between which 64 lies: 49 (since \( 7^2 = 49 \)) and 81 (since \( 9^2 = 81 \)).
   2. Estimate that the square root of 64 is closer to 8, as \( 64 \) is exactly \( 8 \times 8 \).
   3. Therefore, confirm that the square root of 64 is 8.
4. Using a Calculator:
   1. Enter the number 64 into the calculator.
   2. Press the square root function (√) button.
   3. The calculator will display the result: 8.
5. Verification:

   To verify, multiply the result by itself:

   \( 8 \times 8 = 64 \)

   \( 8^2 = 64 \)

   Therefore, the positive square root of 64 is indeed 8.

Square roots can be both positive and negative because both the positive and negative numbers, when squared, yield the original positive number. For example, both 8 and -8 are square roots of 64 because:

\( 8 \times 8 = 64 \) and \( -8 \times -8 = 64 \)

Here's a detailed explanation of positive and negative square roots:

• Principal (Positive) Square Root:

  The principal square root is the non-negative square root of a number. It is the most commonly used square root in mathematical calculations and is represented by the radical symbol \( \sqrt{} \). For instance, the principal square root of 64 is 8, represented as \( \sqrt{64} = 8 \).

• Negative Square Root:

  In addition to the principal square root, every positive number also has a negative square root. This is usually represented as the negative of the principal square root. For 64, the negative square root is -8, represented as \( -\sqrt{64} = -8 \).

• Mathematical Representation:

  When both square roots are considered, they are written as \( \pm \sqrt{x} \), which means both the positive and negative square roots. For example, the square roots of 64 are \( \pm \sqrt{64} = \pm 8 \), which includes both 8 and -8.

To summarize:

• The positive square root of 64 is \( 8 \).
• The negative square root of 64 is \( -8 \).
• Both can be expressed together as \( \pm 8 \).

Understanding both positive and negative square roots is crucial for solving equations and understanding the full set of solutions for quadratic equations. While the principal square root is often used in practical applications, recognizing the negative square root is important in comprehensive mathematical problem-solving.

The positive square root holds significant importance in various mathematical and practical contexts. Understanding its relevance is essential for grasping fundamental concepts and solving real-world problems. Here are some key reasons why the positive square root is important:

• Standard Mathematical Convention:

  In mathematics, the positive square root is typically used as the principal value. This convention simplifies calculations and ensures consistency in solving equations and performing operations.

• Geometry and Measurement:

  The positive square root is crucial in geometry, particularly in calculating the lengths of sides in right triangles, determining the diagonal of squares, and finding the radius of circles. For example, the length of the diagonal of a square with side length 8 units is \( \sqrt{64} = 8 \) units.

• Quadratic Equations:

  Solving quadratic equations often involves finding the square roots of numbers. The positive square root provides one of the two possible solutions, which is particularly useful in practical applications where negative values may not be meaningful.

• Real-World Applications:

  The positive square root is used in various fields such as physics, engineering, finance, and statistics. For instance, in physics, the positive square root is used to calculate distances, velocities, and other physical quantities that must be non-negative.

• Simplification and Clarity:

  Using the positive square root simplifies expressions and makes it easier to interpret results. For example, when dealing with areas, volumes, or other measurements, the positive value provides a clear and practical answer.

To illustrate the importance of the positive square root, consider the following example:

\( \text{Area of a square} = 64 \, \text{square units} \)

\( \text{Side length} = \sqrt{64} = 8 \, \text{units} \)

Here, the positive square root (8) gives a meaningful measurement of the side length, whereas the negative value would not make sense in this context.

In summary, the positive square root is a fundamental concept that plays a vital role in mathematics and its applications, providing clear, practical, and consistent results in a wide range of scenarios.

The positive square root of 64 is 8. Understanding the applications of this value is crucial in various fields:

• Mathematics: In mathematics, 8 is used in calculations involving geometry, algebra, and trigonometry.
• Engineering: Engineers utilize the square root of 64 in designing structures, determining distances, and calculating velocities.
• Physics: Physicists apply the value 8 in equations related to motion, energy, and fluid dynamics.
• Technology: In computing and digital signal processing, the square root of 64 influences algorithms and data analysis.
• Economics: Economists use 8 in statistical models and financial projections.

The positive square root of 64 is 8. Here are some specific applications of this value in geometry:

• Circle: The radius of a circle with an area of 64 square units is 8 units, as \( r = \sqrt{64} \).
• Square: In a square with an area of 64 square units, each side measures 8 units, since \( s = \sqrt{64} \).
• Right Triangle: The sides of a right triangle with legs of length 8 units each have a hypotenuse of 8√2 units, where \( c = \sqrt{2 \times 64} \).
• Volume: The side length of a cube with a volume of 512 cubic units is 8 units, calculated as \( s = \sqrt[3]{512} \).
• Perimeter: The perimeter of a square with a side length of 8 units is 32 units, as \( P = 4 \times 8 \).

The positive square root of 64 is 8. Here are several algebraic applications of this value:

• Equations: Solving equations like \( x^2 = 64 \) yields \( x = \pm 8 \), where the positive solution is 8.
• Factoring: Factoring quadratic expressions such as \( x^2 - 64 \) results in \( (x - 8)(x + 8) \).
• Exponents: Simplifying expressions involving powers, for example \( 8^2 = 64 \).
• Radicals: Simplifying radical expressions like \( \sqrt{64} = 8 \).
• Quadratic Functions: The vertex form of a quadratic function \( f(x) = ax^2 + bx + c \) with \( a = 1 \), \( b = 0 \), and \( c = -64 \) has a vertex at \( x = 8 \).

Understanding the positive square root of 64 can lead to answering several common questions:

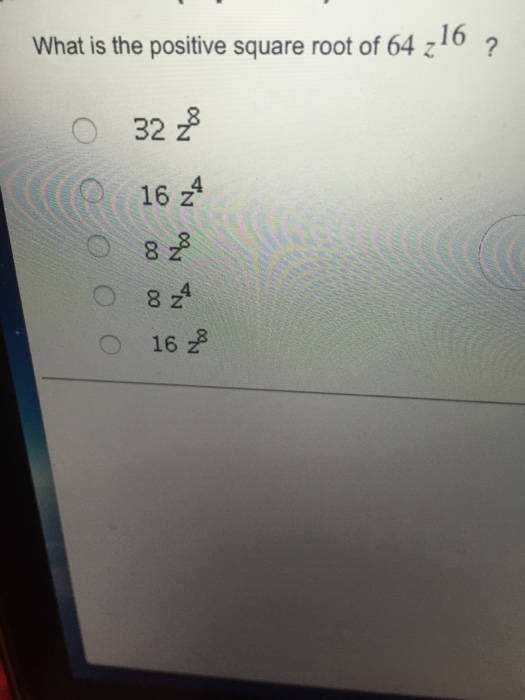
1. What is the positive square root of 64?

   The positive square root of 64 is 8.

2. Why is the positive square root of 64 important?

   It is important because it represents the length or value that, when multiplied by itself, gives 64. In various applications, knowing this value is crucial for calculations.

3. How do you calculate the positive square root of 64?

   It can be calculated using different methods, including manual calculation, using a calculator, or through programming. Mathematically, \( \sqrt{64} = 8 \).

4. What are the practical uses of knowing the positive square root of 64?

   Knowing the square root of 64 is useful in fields such as geometry for calculating dimensions, algebra for solving equations, physics for understanding velocities, and more.

5. Can the positive square root of 64 be negative?

   No, by definition, the positive square root refers to the non-negative solution of the square root operation. Therefore, the positive square root of 64 is specifically 8.

Finding the square root of 64 manually involves several steps:

1. Estimation: Begin by estimating the square root. For 64, a reasonable estimate is 8, since \( 8^2 = 64 \).
2. Refinement: To refine the estimate, use the Babylonian method or divide-and-average method.
3. Iteration: Iterate using the formula \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{64}{x_n} \right) \) until you achieve a satisfactory level of accuracy.
4. Verification: Verify your result by squaring the obtained square root. For 8, \( 8^2 = 64 \), confirming that \( \sqrt{64} = 8 \).

Calculating the square root of 64 using a calculator is straightforward:

1. Enter the Number: Turn on your calculator and input the number 64.
2. Find the Square Root: Press the square root button (often denoted as \( \sqrt{x} \) or \( x^{0.5} \)).
3. Obtain the Result: The calculator will display the result, which is 8.
4. Verify: Verify the result by squaring the calculated square root. For 8, \( 8^2 = 64 \), confirming \( \sqrt{64} = 8 \).

Exploring advanced concepts related to the square root of 64:

• Complex Numbers: In the realm of complex numbers, \( \sqrt{64} \) includes not only 8 but also -8, considering both positive and negative roots.
• Function Properties: The square root function \( f(x) = \sqrt{x} \) is defined for \( x \geq 0 \) and is continuous and differentiable within its domain.
• Algebraic Structures: Within algebraic structures like fields and rings, properties of square roots are essential for solving equations and understanding number theory.
• Applications in Calculus: In calculus, the concept extends to limits and derivatives involving square roots, integral calculus, and applications in optimization problems.
• Historical Development: Historically, the understanding of square roots has evolved from geometric methods to algebraic and computational techniques, shaping mathematical thought.

Understanding square roots of perfect squares such as 64:

• Definition: A perfect square is an integer that is the square of an integer. For 64, \( 64 = 8^2 \), so the square root is 8.
• Properties: The square root of a perfect square is always an integer. It has both positive and negative roots, but the positive square root conventionally refers to the non-negative solution.
• Calculation: Calculating the square root of a perfect square involves identifying the number whose square equals the perfect square.
• Applications: Perfect squares and their roots are fundamental in mathematics, used in geometry, algebra, and various scientific disciplines.
• Examples: Examples of perfect squares include \( 1^2 = 1 \), \( 2^2 = 4 \), \( 3^2 = 9 \), and so on.

Exploring square roots of non-perfect squares, such as 64:

• Definition: A non-perfect square is a number that is not the square of an integer. For example, \( \sqrt{64} \) is considered a perfect square because \( 64 = 8^2 \).
• Approximation: Non-perfect square roots are irrational numbers and cannot be represented exactly as fractions or terminating decimals.
• Calculation: Approximating \( \sqrt{64} \) involves methods like decimal approximation, continued fractions, or iterative algorithms.
• Examples: Other non-perfect square roots include \( \sqrt{2}, \sqrt{3}, \sqrt{5}, \) and so on, which cannot be expressed exactly as integers or simple fractions.
• Applications: Non-perfect square roots are crucial in fields like geometry, physics, and engineering for precise measurements and calculations.

Understanding the positive square root of 64, which is 8, is essential for various mathematical and practical applications. Throughout this guide, we've explored:

• The definition and calculation of square roots.
• Applications of the square root of 64 in geometry, algebra, and other fields.
• Methods for finding square roots manually and using calculators.
• Advanced concepts related to square roots, including perfect and non-perfect squares.

Knowing the square root of 64 not only aids in solving mathematical equations but also has practical implications in fields such as engineering, physics, and economics. As you continue to explore mathematics, understanding square roots will prove invaluable in both academic and real-world scenarios.