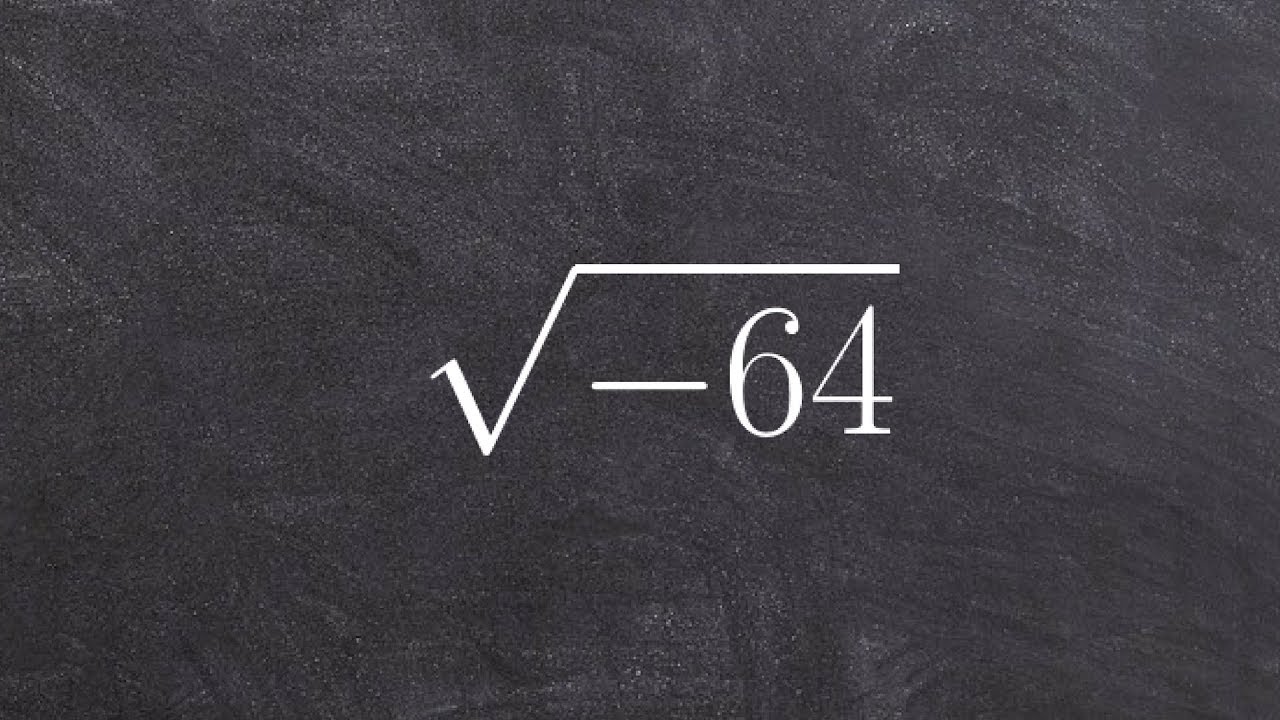What is the Square Root of 68? Discover the Answer and More!

The square root of 68 is approximately represented as:

\( \sqrt{68} \approx 8.246211251235321 \)

The concept of square roots is fundamental in mathematics. A square root of a number is a value that, when multiplied by itself, gives the original number. For instance, the square root of 68 is a number that, when squared, equals 68. This guide will explore the definition, calculation, and significance of square roots.

Mathematically, the square root of a number \( x \) is denoted as \( \sqrt{x} \). For example:

\[ \sqrt{68} \approx 8.246 \]

Understanding square roots involves several key concepts:

• Definition: A square root of a number \( n \) is a number \( m \) such that \( m^2 = n \).
• Notation: The square root symbol \( \sqrt{} \) is used to denote the square root. For example, \( \sqrt{68} \).
• Positive and Negative Roots: Every positive number has two square roots, one positive and one negative, because \( ( -a )^2 = a^2 \).

Calculating the square root of 68 involves several methods:

1. Prime Factorization: Breaking down 68 into its prime factors to simplify the square root.
2. Approximation: Using methods such as the Babylonian method for an iterative approximation.
3. Calculator: Using a scientific calculator to find the square root quickly and accurately.

Let's delve deeper into these methods and their applications in the following sections.

A square root of a number is a value that, when multiplied by itself, yields the original number. In mathematical terms, for a given number \( x \), its square root is denoted as \( \sqrt{x} \). For example, the square root of 68 is written as \( \sqrt{68} \).

To better understand this concept, consider the following properties and examples:

• Basic Definition: If \( y \) is the square root of \( x \), then \( y \times y = x \). This can also be written as \( y^2 = x \).
• Positive and Negative Roots: Every positive number has two square roots, one positive and one negative. For instance, the square roots of 68 are approximately \( 8.246 \) and \( -8.246 \), since \( 8.246^2 = 68 \) and \( (-8.246)^2 = 68 \).

Let's look at an example to illustrate this:

If \( x = 68 \), then:

\[ \sqrt{68} \approx 8.246 \]

This means:

\[ 8.246 \times 8.246 \approx 68 \]

The concept of square roots extends beyond simple calculations. They play a crucial role in various mathematical fields, including algebra, geometry, and calculus. Understanding square roots helps in solving quadratic equations, determining distances in coordinate geometry, and analyzing real-world phenomena in physics and engineering.

To summarize, a square root is a fundamental mathematical concept that finds widespread application across different disciplines. It simplifies complex problems and provides a deeper understanding of numerical relationships.

The square root of a number is a value that, when multiplied by itself, gives the original number. Mathematically, if \( y \) is the square root of \( x \), then \( y \times y = x \) or \( y^2 = x \). This relationship can be expressed as:

\[ \sqrt{x} = y \]

where \( \sqrt{x} \) denotes the square root of \( x \) and \( y \) is the resulting value.

For example, the square root of 68 is denoted as \( \sqrt{68} \). To verify this, we can perform the following calculation:

\[ y = \sqrt{68} \approx 8.246 \]

To confirm, we can square the result:

\[ 8.246 \times 8.246 \approx 68 \]

Thus, \( \sqrt{68} \approx 8.246 \).

The square root function has several important properties:

• Non-negativity: The square root of a non-negative number is always non-negative. For instance, \( \sqrt{68} \) is approximately 8.246, not -8.246, because the square root function typically returns the principal (non-negative) root.
• Product Property: The square root of a product is equal to the product of the square roots of the factors. Mathematically, \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \).
• Quotient Property: The square root of a quotient is equal to the quotient of the square roots of the numerator and denominator. Mathematically, \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \), where \( b \neq 0 \).

In summary, the square root of a number \( x \) is a value \( y \) such that \( y^2 = x \). It is a fundamental concept in mathematics with various properties that simplify calculations and problem-solving in different fields.

Calculating the square root of 68 can be approached using various methods, each offering a different level of precision and computational effort. Here are some common methods to find \( \sqrt{68} \):

1. Prime Factorization Method:

This method involves breaking down 68 into its prime factors. However, 68 is not a perfect square, so this method doesn't simplify it exactly but helps in understanding the factors:

\[ 68 = 2 \times 34 = 2 \times 2 \times 17 \]

Since 68 cannot be written as a product of two identical factors, we move on to other methods.

2. Approximation Method (Babylonian Method):

The Babylonian method, also known as Heron's method, is an iterative approach to approximate square roots. Here's how it works for \( \sqrt{68} \):




1. Start with an initial guess, say 8.


2. Use the formula:
   \[ \text{New Guess} = \frac{1}{2} \left( \text{Old Guess} + \frac{68}{\text{Old Guess}} \right) \]
   


3. Repeat until the guess stabilizes.



Applying this:

Initial guess: 8

First iteration:
\[ \text{New Guess} = \frac{1}{2} \left( 8 + \frac{68}{8} \right) = \frac{1}{2} \left( 8 + 8.5 \right) = \frac{16.5}{2} = 8.25 \]

Second iteration:
\[ \text{New Guess} = \frac{1}{2} \left( 8.25 + \frac{68}{8.25} \right) \approx 8.246 \]

Further iterations will yield a more precise approximation, which shows that \( \sqrt{68} \approx 8.246 \).

3. Using a Calculator:

The most straightforward way to find the square root of 68 is by using a scientific calculator. Enter 68 and press the square root button to get:
\[ \sqrt{68} \approx 8.246211251235321 \]

These methods provide a comprehensive approach to understanding and calculating the square root of 68, catering to different needs and levels of precision.

Finding the square root of a number can be achieved through several methods, each suited for different levels of accuracy and mathematical complexity. Here, we explore some common techniques used to determine square roots, including the square root of 68.

1. Prime Factorization Method:

This method involves expressing the number as a product of its prime factors and then simplifying. However, since 68 is not a perfect square, prime factorization helps understand its factors but does not provide an exact square root:
\[ 68 = 2 \times 34 = 2 \times 2 \times 17 \]

2. Babylonian Method (Iterative Approximation):

The Babylonian method, or Heron's method, is an ancient algorithm for approximating square roots. It involves the following steps:




1. Choose an initial guess. For example, 8.


2. Use the iterative formula:
   \[ \text{New Guess} = \frac{1}{2} \left( \text{Old Guess} + \frac{68}{\text{Old Guess}} \right) \]
   


3. Repeat the process until the guess converges to a stable value.



For \( \sqrt{68} \):

Initial guess: 8

First iteration:
\[ \text{New Guess} = \frac{1}{2} \left( 8 + \frac{68}{8} \right) = \frac{1}{2} \left( 8 + 8.5 \right) = 8.25 \]

Second iteration:
\[ \text{New Guess} = \frac{1}{2} \left( 8.25 + \frac{68}{8.25} \right) \approx 8.246 \]

This iterative process shows that \( \sqrt{68} \approx 8.246 \).

3. Long Division Method:

The long division method is a manual technique to find the square root of a number with high precision. Here's how it works for \( \sqrt{68} \):




1. Group the digits in pairs, starting from the decimal point. For 68, write it as 68.00.


2. Find the largest number whose square is less than or equal to 68. This is 8, since \( 8^2 = 64 \).


3. Subtract \( 64 \) from \( 68 \), giving a remainder of 4. Bring down the next pair of zeros to get 400.


4. Double the divisor (8) to get 16. Find the next digit \( x \) such that \( 16x \times x \leq 400 \). The digit is 2, since \( 162 \times 2 = 324 \).


5. Continue the process to get a more precise value.



This method shows that \( \sqrt{68} \approx 8.246 \).

4. Using a Calculator:

The simplest and quickest method is to use a scientific calculator. Enter the number 68 and press the square root button (\(\sqrt{}\)). The calculator will display:
\[ \sqrt{68} \approx 8.246211251235321 \]

These methods demonstrate the versatility and depth of approaches available for calculating square roots, catering to various needs from manual precision to quick digital computations.

When calculating the square root of a non-perfect square like 68, approximation techniques are invaluable for achieving accurate results. Here, we explore several methods for approximating \( \sqrt{68} \).

1. Babylonian Method (Iterative Method):

The Babylonian method, also known as Heron's method, is an iterative technique to approximate square roots. The steps are as follows:




1. Choose an initial guess. Let's start with 8.


2. Apply the formula:
   \[ \text{New Guess} = \frac{1}{2} \left( \text{Old Guess} + \frac{68}{\text{Old Guess}} \right) \]
   


3. Repeat until the guess stabilizes.



For \( \sqrt{68} \):

Initial guess: 8

First iteration:
\[ \text{New Guess} = \frac{1}{2} \left( 8 + \frac{68}{8} \right) = \frac{1}{2} \left( 8 + 8.5 \right) = 8.25 \]

Second iteration:
\[ \text{New Guess} = \frac{1}{2} \left( 8.25 + \frac{68}{8.25} \right) \approx 8.246 \]

Continued iterations will further refine the approximation, showing that \( \sqrt{68} \approx 8.246 \).

2. Linear Approximation:

Linear approximation uses the tangent line to estimate the square root. For \( \sqrt{68} \), we use a nearby perfect square, such as 64 (\( \sqrt{64} = 8 \)), to estimate:




1. Let \( f(x) = \sqrt{x} \). The derivative is \( f'(x) = \frac{1}{2\sqrt{x}} \).


2. At \( x = 64 \), \( f(64) = 8 \) and \( f'(64) = \frac{1}{2 \times 8} = \frac{1}{16} \).


3. Using the linear approximation formula \( f(x) \approx f(a) + f'(a)(x - a) \), where \( a = 64 \) and \( x = 68 \):
   \[ \sqrt{68} \approx 8 + \frac{1}{16}(68 - 64) = 8 + \frac{4}{16} = 8 + 0.25 = 8.25 \]
   



This provides a close approximation of \( \sqrt{68} \).

3. Average Method:

This simple method averages two close estimates:




1. Choose two close numbers. For 68, consider 8 and 8.5.


2. Calculate the average:
   \[ \text{Average} = \frac{8 + 8.5}{2} = 8.25 \]
   



This method is less precise but provides a quick approximation.

These approximation techniques, ranging from iterative to linear methods, demonstrate how to estimate the square root of 68 effectively and efficiently.

Calculating the square root of a number using a calculator is the most straightforward and accurate method available. Here's a step-by-step guide to finding the square root of 68 using a scientific calculator:

1. Turn on the Calculator:

Ensure your calculator is powered on and functioning correctly.

2. Locate the Square Root Button:

Identify the square root function on your calculator, usually represented by the symbol \( \sqrt{} \) or sometimes as "sqrt".

3. Input the Number:

Enter the number 68 using the numeric keypad on the calculator.

4. Apply the Square Root Function:

Press the square root button (\( \sqrt{} \)) to compute the square root of 68.

5. Read the Result:

The display will show the result of the square root calculation. For 68, the calculator will display:
\[ \sqrt{68} \approx 8.246211251235321 \]

Using a calculator to find the square root is not only quick but also provides a high level of precision, making it ideal for both simple and complex calculations. Here are a few tips to ensure accurate results:

• Double-check Input: Ensure that you have entered the correct number before pressing the square root button.
• Use Scientific Calculators: For more precise results, use a scientific calculator that can handle larger and more complex numbers.
• Verify Results: If possible, cross-check your results using different methods or calculators to confirm accuracy.

In summary, using a calculator to find the square root of 68 is an efficient method that ensures accuracy and saves time, making it a preferred choice for both students and professionals.

The square root of 68 is a number that, when multiplied by itself, gives the product 68. This number cannot be expressed as an exact integer, and thus, its decimal representation is important for practical purposes.

To understand the decimal representation of the square root of 68, we can approximate it using various methods. The most common approach is using a calculator, which provides a precise decimal value.

The square root of 68 is approximately:

√68 ≈ 8.246211251235321

Here is a step-by-step breakdown of the decimal representation:

1. Identify the closest perfect squares around 68. These are 64 (8²) and 81 (9²).
2. Since 68 lies between 64 and 81, its square root will be between 8 and 9.
3. Using a calculator, we find a more precise value of √68, which is approximately 8.246211251235321.

For practical purposes, you might use the square root of 68 rounded to different decimal places, depending on the required precision:

• Rounded to 1 decimal place: 8.2
• Rounded to 2 decimal places: 8.25
• Rounded to 3 decimal places: 8.246
• Rounded to 4 decimal places: 8.2462

To visualize how close this approximation is, consider the following squares:

• 8.2² = 67.24
• 8.25² = 68.0625
• 8.246² = 67.988516
• 8.2462² = 68.00006724

Each step brings us closer to the precise value of 68. Therefore, using the square root in its decimal form allows for accurate and practical computations in various applications.

The square root of 68 has several interesting properties. Here, we explore these properties in detail.

Simplified Radical Form

The square root of 68 can be expressed in its simplest radical form. By factoring 68, we get:

\(\sqrt{68} = \sqrt{4 \times 17} = \sqrt{4} \times \sqrt{17} = 2\sqrt{17}\)

Decimal Representation

When expressed as a decimal, the square root of 68 is approximately:

\(\sqrt{68} \approx 8.246211251\)

This is a non-repeating, non-terminating decimal, confirming that the square root of 68 is an irrational number.

Positive and Negative Roots

The square root of 68 has both positive and negative values. Therefore, we can write:

\(\sqrt{68} = \pm 8.246211251\)

Properties and Usage

• Irrational Number: The square root of 68 cannot be expressed as a fraction of two integers, making it an irrational number.
• Application in Geometry: This value is often used in geometric calculations, such as finding the diagonal length of a rectangle with sides of lengths 4 and \(\sqrt{17}\).
• Exponential Form: The square root of 68 can also be expressed using exponents as \(68^{1/2}\).

Approximation Techniques

Various methods can approximate the square root of 68:

1. Long Division Method: A manual method to approximate the square root by dividing and averaging.
2. Newton-Raphson Method: An iterative numerical technique to find increasingly accurate approximations.
3. Babylonian Method: Also known as Heron's method, which involves averaging and iterating.

Understanding the properties of the square root of 68 helps in various mathematical and practical applications, enhancing our ability to solve complex problems with greater precision.

The square root of 68 can be simplified by identifying the largest perfect square factor of 68. Here is a step-by-step process to find the simplest radical form:

1. First, factorize 68 into its prime factors:

   • 68 = 2 × 34
   • 34 = 2 × 17

   So, 68 can be written as:

   \[ 68 = 2^2 \times 17 \]

2. Apply the product rule for radicals, which states that \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\):

   \[ \sqrt{68} = \sqrt{2^2 \times 17} \]

3. Simplify the square root of the perfect square (2²):

   \[ \sqrt{2^2 \times 17} = \sqrt{2^2} \times \sqrt{17} \]

   \[ \sqrt{2^2} = 2 \]

4. Combine the simplified parts to get the simplest radical form:

   \[ \sqrt{68} = 2 \sqrt{17} \]

Therefore, the square root of 68 in its simplest radical form is \(2 \sqrt{17}\).

The prime factorization method is a systematic way to find the square root of a number by expressing it as a product of prime factors. Here is how to find the square root of 68 using prime factorization:

1. Prime Factorization:

   First, decompose 68 into its prime factors:

   \[ 68 = 2 \times 2 \times 17 \]

2. Pairing the Factors:

   Identify pairs of prime factors. Each pair of identical prime factors represents a square:

   \[ 68 = (2 \times 2) \times 17 \]

   We can rewrite this as:

   \[ 68 = 2^2 \times 17 \]

3. Taking the Square Root:

   Take the square root of both sides of the equation. The square root of a product is the product of the square roots:

   \[ \sqrt{68} = \sqrt{2^2 \times 17} \]

   Simplify this using the property of square roots:

   \[ \sqrt{68} = \sqrt{2^2} \times \sqrt{17} \]

   \[ \sqrt{68} = 2 \times \sqrt{17} \]

Therefore, the square root of 68 in simplest radical form is \( 2\sqrt{17} \).

Estimating the square root of a number manually can be done using various methods. One common approach is the approximation technique, which involves a few steps to get a close estimate. Here’s a detailed step-by-step guide to manually estimate the square root of 68:

1. Identify Perfect Squares:

   First, identify the perfect squares that are closest to 68. The perfect squares around 68 are:

   • \(64\) (which is \(8^2\))
   • \(81\) (which is \(9^2\))
2. Choose the Initial Estimate:

   Since 68 lies between 64 and 81, its square root will be between the square roots of these two numbers. Therefore:

   \(8 < \sqrt{68} < 9\)

3. Refine the Estimate:

   To refine the estimate, we can use the average method. Calculate the midpoint between 8 and 9:

   \(\text{Midpoint} = \frac{8 + 9}{2} = 8.5\)

   Square 8.5 to see how close it is to 68:

   \(8.5^2 = 72.25\)

   Since 72.25 is greater than 68, we know our estimate should be less than 8.5. Next, choose a number between 8 and 8.5, such as 8.3:

4. Further Refinement:

   Square 8.3 to check its proximity to 68:

   \(8.3^2 = 68.89\)

   Since 68.89 is still greater than 68, choose a number slightly less than 8.3, such as 8.2:

5. Check the New Estimate:

   Square 8.2 to check its proximity to 68:

   \(8.2^2 = 67.24\)

   Now, 67.24 is slightly less than 68, so our estimate should be slightly more than 8.2. We can try 8.25:

6. Final Refinement:

   Square 8.25 to check its proximity to 68:

   \(8.25^2 = 68.0625\)

   Since 68.0625 is very close to 68, we can conclude that the square root of 68 is approximately 8.25.

By following these steps, you can manually estimate the square root of 68 to a reasonable degree of accuracy.

Square roots have a wide range of applications in real life, making them a fundamental concept in various fields. Here are some detailed examples of how square roots are used in everyday scenarios:

1. Geometry and Construction:

   Square roots are essential in geometry, especially when dealing with right triangles. The Pythagorean theorem states that in a right triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. This theorem is widely used in construction and engineering to ensure structures are built correctly. For example, to find the length of the diagonal of a square room with side length \(10\) meters:

   \[
   \text{Diagonal} = \sqrt{10^2 + 10^2} = \sqrt{200} = 10\sqrt{2} \approx 14.14 \text{ meters}
   \]

2. Physics:

   In physics, square roots are used in various equations to describe natural phenomena. For example, the formula for the period \(T\) of a simple pendulum is:

   \[
   T = 2\pi \sqrt{\frac{L}{g}}
   \]

   where \(L\) is the length of the pendulum and \(g\) is the acceleration due to gravity. This equation shows how the period of the pendulum depends on the square root of its length.

3. Finance:

   In finance, the square root is used to calculate the standard deviation, which measures the amount of variation or dispersion in a set of values. The standard deviation is crucial for assessing risk and volatility in financial markets. The formula for standard deviation \(\sigma\) is:

   \[
   \sigma = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (x_i - \mu)^2}
   \]

   where \(N\) is the number of observations, \(x_i\) is each individual observation, and \(\mu\) is the mean of the observations.

4. Technology and Engineering:

   Square roots are used in signal processing and electrical engineering. For example, in calculating the root mean square (RMS) value of an alternating current (AC) signal, which is important for designing electrical systems. The RMS value of a signal \(V(t)\) over a period \(T\) is given by:

   \[
   V_{RMS} = \sqrt{\frac{1}{T} \int_0^T V(t)^2 \, dt}
   \]

5. Medicine:

   Square roots are used in various medical calculations, including the Body Surface Area (BSA), which is used to determine the correct dosage of medication for patients. The BSA can be estimated using the Mosteller formula:

   \[
   BSA (\text{m}^2) = \sqrt{\frac{\text{height (cm)} \times \text{weight (kg)}}{3600}}
   \]

These examples illustrate the importance of understanding square roots, as they play a crucial role in multiple disciplines, impacting various aspects of our daily lives.

Square roots play a fundamental role in geometry, especially when dealing with measurements, areas, and distances. Here are some key applications of square roots in geometric contexts:

1. Pythagorean Theorem:

   The Pythagorean Theorem is one of the most well-known applications of square roots in geometry. It states that in a right triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. Mathematically, this is expressed as:

   \[
   c = \sqrt{a^2 + b^2}
   \]

   where \(c\) is the hypotenuse and \(a\) and \(b\) are the other two sides. For example, if \(a = 5\) and \(b = 12\):

   \[
   c = \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13
   \]

2. Diagonal of a Square:

   The length of the diagonal of a square can be found using the square root. For a square with side length \(s\), the diagonal \(d\) is given by:

   \[
   d = s\sqrt{2}
   \]

   If the side length of the square is \(10\) units, the diagonal would be:

   \[
   d = 10\sqrt{2} \approx 14.14 \text{ units}
   \]

3. Area of a Right Triangle:

   The area \(A\) of a right triangle can be determined if the lengths of the legs are known. Using the Pythagorean Theorem to find the hypotenuse and then calculating the area:

   \[
   A = \frac{1}{2} \times a \times b
   \]

   If \(a = 6\) units and \(b = 8\) units, then:

   \[
   A = \frac{1}{2} \times 6 \times 8 = 24 \text{ square units}
   \]

4. Circle and Radius Relationships:

   The distance from the center of a circle to any point on the circumference is the radius \(r\). If you know the diameter \(d\), the radius can be found using:

   \[
   r = \frac{d}{2}
   \]

   Conversely, if you know the area \(A\) of the circle, the radius can be determined by:

   \[
   r = \sqrt{\frac{A}{\pi}}
   \]

   If the area of the circle is \(50\) square units:

   \[
   r = \sqrt{\frac{50}{\pi}} \approx 3.99 \text{ units}
   \]

5. Distance Formula:

   The distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) in a plane can be found using the distance formula, which is derived from the Pythagorean Theorem:

   \[
   d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
   \]

   If the points are \((3, 4)\) and \((7, 1)\), the distance \(d\) is:

   \[
   d = \sqrt{(7 - 3)^2 + (1 - 4)^2} = \sqrt{4^2 + (-3)^2} = \sqrt{16 + 9} = \sqrt{25} = 5
   \]

These applications show how essential square roots are in solving geometric problems, helping to calculate distances, areas, and other important properties in various geometric shapes.

Square roots are widely used in physics to solve various equations and understand natural phenomena. Here are some key applications of square roots in physics:

1. Kinematics and Motion:

   In kinematics, the equations of motion often involve square roots. For example, the formula for the time \(t\) it takes for an object to fall from a height \(h\) with an initial velocity \(v_0\) under the acceleration due to gravity \(g\) is given by:

   \[
   t = \frac{v_0 \pm \sqrt{v_0^2 + 2gh}}{g}
   \]

   This equation helps calculate the time required for an object to reach the ground.

2. Energy and Work:

   In the study of energy, particularly kinetic energy, square roots are used. The kinetic energy \(E_k\) of an object with mass \(m\) and velocity \(v\) is given by:

   \[
   E_k = \frac{1}{2}mv^2
   \]

   If we need to solve for velocity \(v\) from kinetic energy, we rearrange the equation:

   \[
   v = \sqrt{\frac{2E_k}{m}}
   \]

3. Wave Physics:

   In wave physics, the relationship between the speed of a wave \(v\), its frequency \(f\), and its wavelength \(\lambda\) involves square roots. The speed of a wave in a stretched string, for instance, is given by:

   \[
   v = \sqrt{\frac{T}{\mu}}
   \]

   where \(T\) is the tension in the string and \(\mu\) is the linear mass density. This formula is crucial for understanding the behavior of waves in different media.

4. Gravitational Potential Energy:

   The formula for escape velocity, which is the minimum speed needed for an object to escape from the gravitational influence of a planet, involves square roots. The escape velocity \(v_e\) from a planet of mass \(M\) and radius \(R\) is given by:

   \[
   v_e = \sqrt{\frac{2GM}{R}}
   \]

   where \(G\) is the gravitational constant. This calculation is essential for space missions and understanding celestial mechanics.

5. Electric Fields and Potentials:

   In electrostatics, the electric potential \(V\) due to a point charge \(q\) at a distance \(r\) from the charge is given by:

   \[
   V = \frac{kq}{r}
   \]

   To find the distance \(r\) at which a certain potential \(V\) is measured, we rearrange the formula:

   \[
   r = \frac{kq}{V}
   \]

   where \(k\) is Coulomb's constant. This relationship helps in understanding the distribution of electric fields and potentials around charges.

6. Optics and Light:

   In optics, the lens maker's equation involves square roots to determine the focal length \(f\) of a lens. The equation is given by:

   \[
   \frac{1}{f} = (n - 1) \left( \frac{1}{R_1} - \frac{1}{R_2} \right)
   \]

   where \(n\) is the refractive index of the lens material and \(R_1\) and \(R_2\) are the radii of curvature of the lens surfaces. Solving for \(f\) often involves manipulating square roots.

These applications highlight the crucial role of square roots in various areas of physics, enabling precise calculations and deeper understanding of physical principles.

Square roots are a fundamental mathematical concept that hold significant educational importance. Understanding square roots is crucial for students as it forms the basis for more advanced mathematical and scientific studies. Here are several reasons why learning square roots is essential in education:

1. Foundation for Higher Mathematics:

   Square roots are a stepping stone to more complex topics in algebra, geometry, and calculus. For example, solving quadratic equations often involves square roots, and understanding this concept is necessary for progressing to polynomial functions and other advanced mathematical theories.

2. Problem-Solving Skills:

   Learning how to calculate and approximate square roots enhances students' problem-solving abilities. These skills are essential not only in mathematics but also in everyday situations where logical thinking and analytical skills are required.

3. Geometric Understanding:

   Square roots are vital in geometry, particularly when dealing with right triangles and the Pythagorean theorem. For example, if the lengths of the legs of a right triangle are known, the length of the hypotenuse can be found using the square root:

   \[
   c = \sqrt{a^2 + b^2}
   \]

   where \(a\) and \(b\) are the legs, and \(c\) is the hypotenuse.

4. Application in Science:

   Square roots are used extensively in physics, chemistry, and engineering. Understanding square roots is necessary for grasping concepts such as wave functions, chemical reaction rates, and structural analysis in engineering.

5. Statistical Analysis:

   In statistics, the standard deviation is calculated using square roots. The standard deviation is a measure of the amount of variation or dispersion in a set of values, and it is crucial for interpreting data correctly:

   \[
   \sigma = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (x_i - \mu)^2}
   \]

   where \(\sigma\) is the standard deviation, \(N\) is the number of observations, \(x_i\) are the individual values, and \(\mu\) is the mean.

6. Technological Proficiency:

   With the growing reliance on technology, understanding mathematical concepts like square roots is essential. Many algorithms in computer science and data analysis use square roots for various calculations, such as optimization problems and machine learning algorithms.

7. Critical Thinking and Logical Reasoning:

   Studying square roots helps develop critical thinking and logical reasoning skills. These skills are not only applicable in academics but also in making informed decisions in everyday life and various professional fields.

Overall, the educational importance of square roots cannot be overstated. Mastery of this concept opens the door to a deeper understanding of mathematics and science, enhancing students' analytical abilities and preparing them for future academic and career challenges.

Calculating square roots can be tricky, and several common mistakes can lead to incorrect results. Understanding these errors is crucial for accurate computation and better mathematical proficiency. Here are some common mistakes and how to avoid them:

1. Incorrectly Simplifying Radicals:

   A common mistake is not fully simplifying the radical expression. For example, the square root of 68 can be simplified as follows:

   \[
   \sqrt{68} = \sqrt{4 \times 17} = \sqrt{4} \times \sqrt{17} = 2\sqrt{17}
   \]

   Failing to recognize the factorization can result in incorrect or incomplete answers.

2. Misunderstanding the Square Root of Negative Numbers:

   Another common mistake is not handling the square root of negative numbers correctly. The square root of a negative number is an imaginary number. For instance:

   \[
   \sqrt{-68} = \sqrt{68} \times \sqrt{-1} = 2\sqrt{17}i
   \]

   where \(i\) is the imaginary unit. Neglecting the imaginary unit leads to incorrect results.

3. Rounding Errors:

   When approximating square roots, rounding errors can occur. For instance, approximating \(\sqrt{68}\) as 8.25 instead of the more accurate 8.246 leads to less precise results. To avoid this, use more decimal places for higher precision or a calculator for accurate values.

4. Arithmetic Mistakes:

   Basic arithmetic errors during calculations can lead to incorrect results. For example, incorrectly adding or multiplying intermediate steps can change the outcome. Double-checking calculations helps prevent such errors.

5. Ignoring the Principal Square Root:

   Another common mistake is forgetting that the principal square root is always non-negative. For example, \(\sqrt{68}\) should be 8.246, not -8.246. While both \(\pm 8.246\) are solutions, the principal square root is the positive value.

6. Confusing Square Roots with Division:

   Sometimes, students mistakenly treat the square root symbol as a division symbol. For example, interpreting \(\sqrt{68}\) as \(68 / 2\) instead of finding the actual square root. It's essential to understand the difference between these operations.

7. Forgetting to Simplify Final Answers:

   After performing calculations, it's important to simplify the final answer. For example, if you calculate that \(\sqrt{72} = 6 \sqrt{2}\), ensure the result is in its simplest form to avoid confusion and inaccuracies.

8. Incorrect Use of Calculator Functions:

   Misusing calculator functions can lead to errors. Ensure you are using the square root function correctly and understand the calculator's syntax to avoid mistakes.

By being aware of these common mistakes and understanding how to avoid them, students can improve their accuracy in calculating square roots and enhance their overall mathematical skills.

Practicing square root calculations can help solidify your understanding and improve your skills. Below are some practice problems along with detailed solutions to help you master the concept of square roots.

1. Problem 1: Simplify \(\sqrt{68}\)

   Solution:

   To simplify \(\sqrt{68}\), we need to find its prime factorization:

   \[
   68 = 2 \times 34 = 2 \times 2 \times 17 = 2^2 \times 17
   \]

   Using the property of square roots, \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\):

   \[
   \sqrt{68} = \sqrt{2^2 \times 17} = \sqrt{2^2} \times \sqrt{17} = 2\sqrt{17}
   \]

2. Problem 2: Approximate \(\sqrt{68}\) to three decimal places

   Solution:

   Using a calculator, we find:

   \[
   \sqrt{68} \approx 8.246
   \]

   Thus, the square root of 68 to three decimal places is 8.246.

3. Problem 3: Find the square root of \(\frac{68}{4}\)

   Solution:

   First, simplify the fraction:

   \[
   \frac{68}{4} = 17
   \]

   Next, find the square root of 17:

   \[
   \sqrt{17} \approx 4.123
   \]

4. Problem 4: Solve for \(x\) in the equation \(x^2 = 68\)

   Solution:

   To solve for \(x\), take the square root of both sides:

   \[
   x = \pm\sqrt{68} = \pm 2\sqrt{17}
   \]

   Thus, \(x = 2\sqrt{17}\) or \(x = -2\sqrt{17}\).

5. Problem 5: If the area of a square is 68 square units, find the length of one side.

   Solution:

   Let \(s\) be the length of one side of the square. Then:

   \[
   s^2 = 68
   \]

   Taking the square root of both sides:

   \[
   s = \sqrt{68} = 2\sqrt{17} \approx 8.246
   \]

   Thus, the length of one side of the square is approximately 8.246 units.

6. Problem 6: Express \(\sqrt{68}\) in its simplest radical form.

   Solution:

   We already know from previous problems that:

   \[
   \sqrt{68} = \sqrt{2^2 \times 17} = 2\sqrt{17}
   \]

   Thus, \(\sqrt{68}\) in its simplest radical form is \(2\sqrt{17}\).

These practice problems demonstrate various methods for calculating and simplifying square roots, reinforcing your understanding and ability to handle square root calculations confidently.