Topic what is the principal square root of 64: The principal square root of 64 is a fundamental mathematical concept that everyone should understand. In this article, we'll explore what the principal square root is, how to calculate it, and why it is important. Join us as we uncover the answer and delve into the intriguing world of square roots.
Table of Content
- Understanding the Principal Square Root of 64
- Introduction to Square Roots
- Definition of Principal Square Root
- Mathematical Representation
- Calculating the Principal Square Root of 64
- Examples of Square Root Calculations
- Properties of Square Roots
- Applications of Square Roots in Real Life
- Common Misconceptions About Square Roots
- Importance of Understanding Principal Square Roots
- Summary and Conclusion
- YOUTUBE:
Understanding the Principal Square Root of 64
The principal square root of a number is the non-negative square root of that number. For the number 64, the principal square root can be found as follows:
Definition
The principal square root of 64 is the positive number that, when multiplied by itself, equals 64. Mathematically, this is represented as:
\[\sqrt{64}\]
Calculation
To determine the principal square root of 64, we solve the equation:
\[\sqrt{64} = x\]
where \( x \) is the number we are looking for. Squaring both sides of the equation, we get:
\[(\sqrt{64})^2 = x^2\]
Since the square of the square root of a number returns the original number, we have:
\[64 = x^2\]
To find \( x \), we take the square root of both sides:
\[x = \sqrt{64}\]
The positive value of \( x \) that satisfies this equation is:
\[x = 8\]
Conclusion
Therefore, the principal square root of 64 is:
\[\sqrt{64} = 8\]
In summary, the principal square root of 64 is a fundamental mathematical concept that highlights the importance of understanding square roots and their properties. By recognizing that the principal square root is always the non-negative root, we ensure that the square root of 64 is:
8

READ MORE:
Introduction to Square Roots
Square roots are a fundamental concept in mathematics, representing a value that, when multiplied by itself, yields the original number. Understanding square roots is essential for solving various mathematical problems and for applications in science, engineering, and everyday life.
The square root of a number \( x \) is denoted as \( \sqrt{x} \). For example, the square root of 64 is represented as \( \sqrt{64} \).
There are a few key points to understand about square roots:
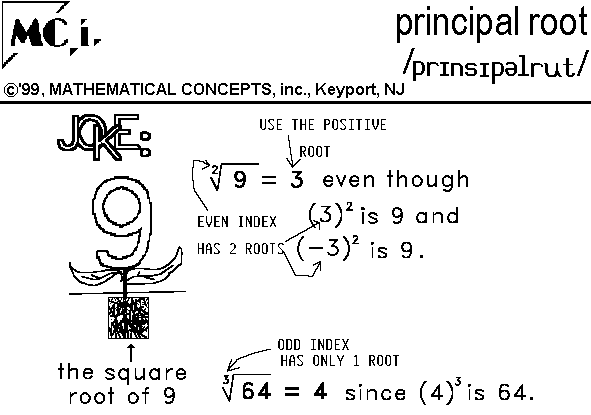
- Each positive number has two square roots: one positive (principal square root) and one negative. For instance, the square roots of 64 are 8 and -8.
- The principal square root is the non-negative square root, which is typically the one referred to in most contexts.
- The principal square root of 64 is 8, since \( 8 \times 8 = 64 \).
Square roots are closely related to the concept of squaring a number. Squaring a number means multiplying the number by itself. For instance, \( 8 \times 8 = 64 \), hence the square root of 64 is 8.
Mathematically, finding the square root of a number is the inverse operation of squaring the number. This relationship can be represented as:
\[
\sqrt{x^2} = x
\]
where \( x \) is a non-negative number.
In summary, understanding square roots allows us to work with equations and expressions involving powers and roots, making it a crucial part of mathematical education and application.
Definition of Principal Square Root
The principal square root of a number is the non-negative root that, when multiplied by itself, gives the original number. It is an essential concept in mathematics, providing a foundation for understanding more complex operations and equations.
To define the principal square root mathematically:
For any non-negative number \( x \), the principal square root is denoted by \( \sqrt{x} \). This is expressed as:
\[
\sqrt{x} = y \quad \text{where} \quad y \geq 0 \quad \text{and} \quad y^2 = x
\]
For example, the principal square root of 64 is determined as follows:
- Identify the number whose square is 64. This number is 8 since \( 8 \times 8 = 64 \).
- Ensure that the root is non-negative. Thus, the principal square root of 64 is 8.
In general, the principal square root function only returns the positive square root of a number, excluding the negative counterpart. Therefore, for any positive number \( x \), \( \sqrt{x} \) always represents the positive root.
Some key properties of the principal square root include:
- The principal square root of 0 is 0, because \( 0 \times 0 = 0 \).
- For any positive number \( x \), \( \sqrt{x} \) is always non-negative.
- The function \( \sqrt{x} \) is continuous and increases as \( x \) increases.
In summary, the principal square root is a fundamental mathematical function that simplifies complex calculations and is widely used in various scientific and engineering applications. Understanding this concept is crucial for mastering higher-level mathematics.
Mathematical Representation
The principal square root of a number is often represented using the radical symbol \(\sqrt{}\). This notation signifies the non-negative root of a given number. Let's explore the mathematical representation of the principal square root step by step.
Consider the number 64. The principal square root of 64 is represented as:
\[
\sqrt{64}
\]
To understand this representation, we need to recognize that finding the principal square root involves identifying the number which, when multiplied by itself, equals the original number. For 64, this can be expressed as:
\[
\sqrt{64} = x \quad \text{where} \quad x^2 = 64
\]
We can solve this equation by determining \( x \) such that:
\[
x = \sqrt{64}
\]
Since \( 8 \times 8 = 64 \), it follows that:
\[
\sqrt{64} = 8
\]
Here are some key points to consider:
- The radical symbol \(\sqrt{}\) is used to denote the principal square root.
- The principal square root is always the positive root of the number.
- The expression \(\sqrt{x}\) implies finding a number \( y \) such that \( y^2 = x \) and \( y \geq 0 \).
For further clarity, let's look at another example with a different number, say 25:
\[
\sqrt{25} = y \quad \text{where} \quad y^2 = 25
\]
Solving for \( y \), we get:
\[
y = \sqrt{25} = 5
\]
Thus, the principal square root of 25 is 5 because \( 5 \times 5 = 25 \).
In summary, the mathematical representation of the principal square root using the radical symbol \(\sqrt{}\) provides a clear and concise way to denote the non-negative root of a number, facilitating easy understanding and application in various mathematical contexts.
Calculating the Principal Square Root of 64
Calculating the principal square root of 64 involves finding the non-negative number that, when multiplied by itself, equals 64. Let's walk through this calculation step by step.
- Understand the Problem:
- We need to find the principal square root of 64, which is denoted as \( \sqrt{64} \).
- Set Up the Equation:
- The principal square root of 64 is the value \( x \) such that \( x^2 = 64 \).
- Mathematically, this is represented as:
\[
\sqrt{64} = x
\]
- Solve the Equation:
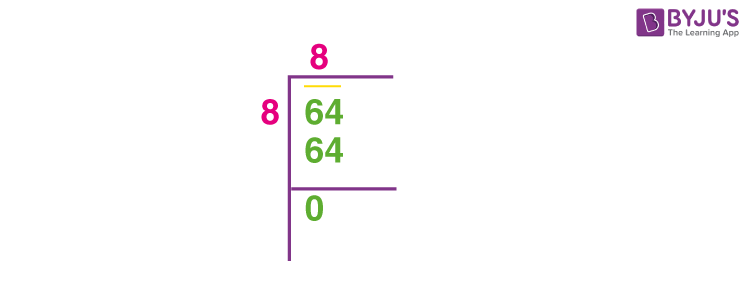
- Identify the number whose square is 64. This number is 8 since \( 8 \times 8 = 64 \).
- Thus, we have:
\[
8^2 = 64
\]
- Verify the Solution:
- To ensure our solution is correct, we can square the result:
\[
8 \times 8 = 64
\] - Since this is true, the principal square root of 64 is indeed 8.
- To ensure our solution is correct, we can square the result:
In summary, the principal square root of 64 is calculated by finding the positive number that squares to 64. Therefore, we conclude:
\[
\sqrt{64} = 8
\]
This method can be applied to find the principal square root of any non-negative number, reinforcing the importance and utility of understanding square roots in mathematics.
Examples of Square Root Calculations
Calculating square roots can be straightforward for perfect squares and more complex for non-perfect squares. Here are some examples to illustrate different scenarios:
Perfect Square Example: \( \sqrt{64} \)
Since 64 is a perfect square, its principal square root is an integer. We calculate:
\[ \sqrt{64} = 8 \]
Thus, the principal square root of 64 is 8.
Perfect Square Example: \( \sqrt{81} \)
81 is also a perfect square. We calculate:
\[ \sqrt{81} = 9 \]
So, the principal square root of 81 is 9.
Non-Perfect Square Example: \( \sqrt{50} \)
50 is not a perfect square, so its square root will be an irrational number. We approximate:
\[ \sqrt{50} \approx 7.07 \]
Using a calculator, the principal square root of 50 is approximately 7.07.
Non-Perfect Square Example: \( \sqrt{20} \)
Similarly, 20 is not a perfect square. We approximate:
\[ \sqrt{20} \approx 4.47 \]
So, the principal square root of 20 is approximately 4.47.
Decimal Example: \( \sqrt{0.25} \)
Calculating the square root of a decimal follows the same principle:
\[ \sqrt{0.25} = 0.5 \]
Therefore, the principal square root of 0.25 is 0.5.
Fraction Example: \( \sqrt{\frac{1}{16}} \)
For fractions, we take the square root of the numerator and the denominator separately:
\[ \sqrt{\frac{1}{16}} = \frac{\sqrt{1}}{\sqrt{16}} = \frac{1}{4} \]
Hence, the principal square root of \( \frac{1}{16} \) is \( \frac{1}{4} \).
Summary Table of Examples
| Expression | Principal Square Root |
|---|---|
| \( \sqrt{64} \) | 8 |
| \( \sqrt{81} \) | 9 |
| \( \sqrt{50} \) | 7.07 (approx.) |
| \( \sqrt{20} \) | 4.47 (approx.) |
| \( \sqrt{0.25} \) | 0.5 |
| \( \sqrt{\frac{1}{16}} \) | 0.25 |
Properties of Square Roots
The properties of square roots are fundamental in understanding how they operate within various mathematical contexts. Here are some key properties:
- Non-negativity: The principal square root of a non-negative number is always non-negative. For example, the principal square root of 64 is 8, not -8, even though both 8 and -8 are solutions to the equation \( x^2 = 64 \).
- Multiplicative Property: The square root of a product is equal to the product of the square roots of the factors. Mathematically, this is represented as: \[ \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \] For instance, \(\sqrt{64} = \sqrt{8 \cdot 8} = 8\).
- Division Property: The square root of a quotient is equal to the quotient of the square roots. This can be expressed as: \[ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \] where \( b \neq 0 \). For example, \(\sqrt{\frac{64}{4}} = \frac{\sqrt{64}}{\sqrt{4}} = \frac{8}{2} = 4\).
- Perfect Squares: The square root of a perfect square (an integer that is the square of another integer) is always an integer. For example, 64 is a perfect square because \(8^2 = 64\).
- Rationality: The square root of a non-negative rational number is either a rational number or an irrational number. For example, \(\sqrt{64} = 8\) is rational, while \(\sqrt{2}\) is irrational.
- Inverse Operation: Squaring and taking the square root are inverse operations. This means: \[ (\sqrt{a})^2 = a \quad \text{and} \quad \sqrt{a^2} = |a| \] For example, \(\sqrt{8^2} = \sqrt{64} = 8\).
- Additivity and Subtractivity: Square roots do not distribute over addition or subtraction: \[ \sqrt{a + b} \neq \sqrt{a} + \sqrt{b} \quad \text{and} \quad \sqrt{a - b} \neq \sqrt{a} - \sqrt{b} \] For instance, \(\sqrt{64 + 36} = \sqrt{100} = 10\), but \(\sqrt{64} + \sqrt{36} = 8 + 6 = 14\).
Understanding these properties allows for better manipulation and simplification of expressions involving square roots, leading to more efficient problem-solving techniques in mathematics.
Applications of Square Roots in Real Life
Square roots are fundamental in various real-life applications across different fields. Here are some notable examples:
- Engineering and Architecture:
Square roots are essential in calculating dimensions and areas, especially when dealing with right triangles and circles. For instance, the Pythagorean theorem, which uses square roots, is critical for determining the lengths of sides in right-angled triangles.
- Physics:
Square roots play a vital role in equations related to motion, force, and energy. For example, in the equation \( v = \sqrt{2gh} \), which calculates the velocity (v) of an object falling from a height (h) under gravity (g), the square root function is used.
- Finance:
In finance, square roots are used in calculating the standard deviation and variance, which are measures of investment risk. The formula for standard deviation involves the square root of the average squared deviations from the mean.
- Medicine:
Square roots are used in various medical calculations, including dosages of medications that depend on body surface area, which can be estimated using the square root of the height and weight of a patient.
- Computer Graphics:
In computer graphics, square roots are used in algorithms for rendering images and animations. Calculating distances between points in 2D and 3D space often involves the use of the square root function.
- Statistics:
Square roots are commonly used in statistical formulas. For instance, the standard error of the mean is calculated by taking the standard deviation divided by the square root of the sample size.
- Astronomy:
Astronomers use square roots in calculations involving the distances between celestial objects and their velocities. The formula for the orbital period of a planet involves the square root of the radius of the orbit cubed.
Common Misconceptions About Square Roots
There are several common misconceptions about square roots that often lead to confusion and errors. Understanding these misconceptions is crucial for a solid grasp of the concept.
-
Misconception 1: The square root of a number always has two values.
Many people believe that the square root of a number has two values, positive and negative. While it's true that the equation \( x^2 = 64 \) has two solutions, \( x = 8 \) and \( x = -8 \), the principal square root of a number is defined to be the non-negative value. Hence, the principal square root of 64 is \( \sqrt{64} = 8 \), not \( \pm 8 \).
-
Misconception 2: Square roots of negative numbers are not possible.
It's a common belief that you cannot take the square root of a negative number. In the realm of real numbers, this is true; however, in the field of complex numbers, the square root of a negative number is possible. For example, \( \sqrt{-64} = 8i \), where \( i \) is the imaginary unit.
-
Misconception 3: The square root function is the inverse of the squaring function for all real numbers.
While the square root function undoes squaring for non-negative numbers, it is not the case for negative numbers. The function \( \sqrt{x^2} \) yields \(|x|\), the absolute value of \(x\), not \(x\) itself. For example, \( \sqrt{(-8)^2} = 8 \), not -8.
-
Misconception 4: Simplifying square roots always results in a simpler form.
Some believe that simplifying square roots always makes the expression simpler. However, simplification depends on the context and the numbers involved. For example, \( \sqrt{50} \) can be simplified to \( 5\sqrt{2} \), but whether this form is simpler or more useful depends on the application.
By addressing and correcting these misconceptions, students and mathematicians can develop a clearer and more accurate understanding of square roots and their properties.
Importance of Understanding Principal Square Roots
Understanding the principal square root is crucial for several reasons:
- Mathematical Foundation: Square roots are fundamental in algebra, geometry, and calculus. Mastery of this concept is essential for understanding more complex mathematical topics.
- Problem Solving: Many real-world problems, especially those involving area and volume, require the use of square roots. For example, determining the side length of a square when given the area.
- Scientific Applications: Square roots are used in physics, engineering, and statistics. For instance, they are crucial in calculating standard deviations in statistics, which measure data variability.
- Technological Relevance: Square roots are vital in computer science and digital imaging. Algorithms for graphics, cryptography, and machine learning often involve square root calculations.
- Everyday Uses: Understanding square roots can help in various daily activities such as determining dimensions for home improvement projects or calculating distances.
By understanding the principal square root, one gains a deeper appreciation of its applications and significance across different fields. This knowledge not only aids in academic pursuits but also enhances problem-solving skills in practical situations.
Summary and Conclusion
The concept of square roots, particularly the principal square root, plays a crucial role in various fields of mathematics and real-life applications. Understanding the principal square root of a number involves recognizing that it is the positive root of that number. For instance, the principal square root of 64 is 8, as \( \sqrt{64} = 8 \), because \( 8^2 = 64 \).
Throughout this article, we have explored several aspects of square roots:
- Introduction to Square Roots: A fundamental mathematical concept where a number is multiplied by itself to yield a given product.
- Definition of Principal Square Root: The non-negative square root of a non-negative number.
- Mathematical Representation: Notations and symbols used to denote square roots, such as the radical symbol (√).
- Calculating the Principal Square Root of 64: Various methods to compute the square root, such as the repeated subtraction, prime factorization, and long division methods.
- Examples of Square Root Calculations: Practical examples to demonstrate how square roots are calculated.
- Properties of Square Roots: Important properties, including the fact that every positive real number has both a positive and a negative square root.
- Applications of Square Roots in Real Life: Real-world scenarios where understanding square roots is essential, such as in geometry, physics, and finance.
- Common Misconceptions About Square Roots: Clarifying typical misunderstandings, like confusing the principal square root with the negative root.
- Importance of Understanding Principal Square Roots: Highlighting the significance of this mathematical concept in education and practical applications.
By comprehending these aspects, students and professionals can better appreciate the utility of square roots in problem-solving and analytical thinking. The principal square root, as a concept, not only simplifies mathematical expressions but also finds extensive use in various scientific and engineering domains.
In conclusion, mastering the principal square root and its properties is fundamental to advancing in mathematical studies and applying these principles effectively in real-world contexts.
Căn Bậc Hai Của 64