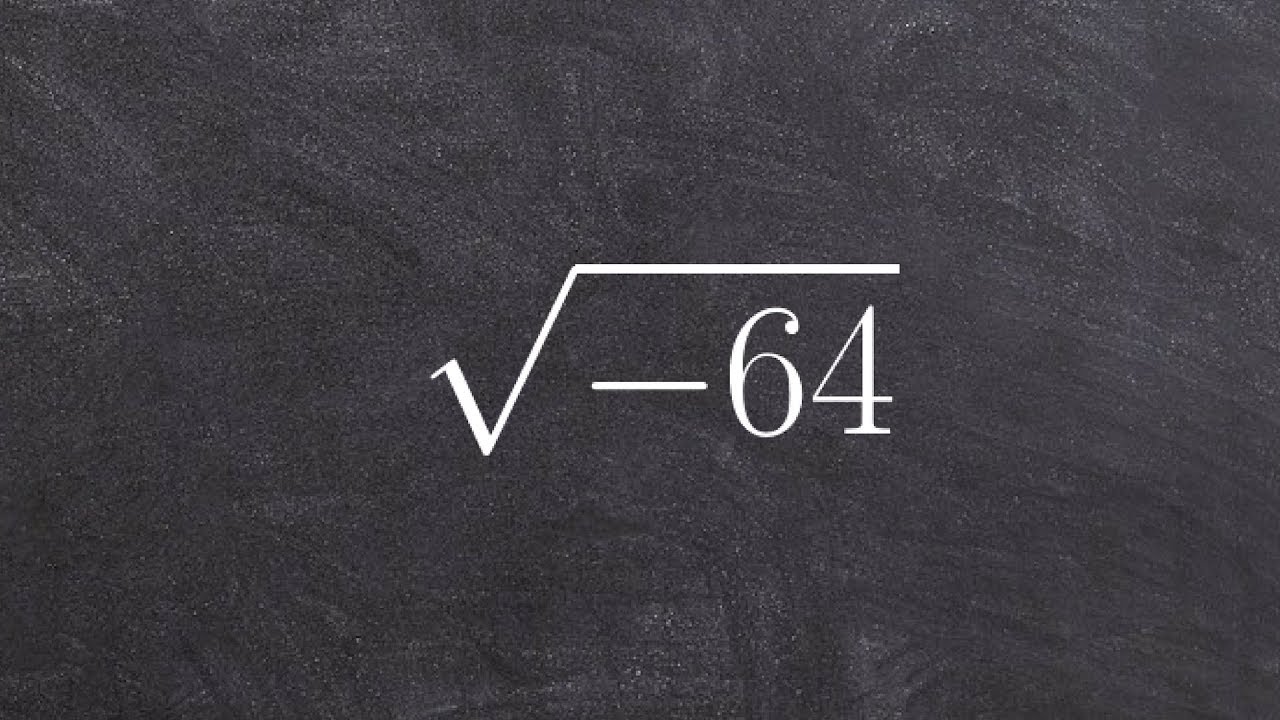Topic is the square root of 64 rational: Is the square root of 64 rational? Absolutely! Delve into the fascinating world of numbers as we explore why 64's square root is not just any number, but a rational one. Uncover the proof, understand the properties, and see real-world examples that make this mathematical concept clear and intriguing.
Table of Content
- Is the Square Root of 64 Rational?
- Introduction
- Understanding Rational Numbers
- Properties of Rational Numbers
- Definition and Calculation of Square Roots
- The Square Root of 64
- Proof of Rationality for the Square Root of 64
- Examples of Rational and Irrational Numbers
- Comparing Rational and Irrational Numbers
- YOUTUBE: Tìm hiểu về căn bậc hai của 64 và tại sao nó là một số hữu tỉ. Video giải thích chi tiết và dễ hiểu để thu hút người xem.
Is the Square Root of 64 Rational?
The question of whether the square root of 64 is rational can be answered by understanding the definitions and properties of rational numbers and square roots.
Definition of a Rational Number
A rational number is any number that can be expressed as the quotient or fraction p/q of two integers, where p and q are integers and q is not zero. Rational numbers include integers, finite decimals, and repeating decimals.
Calculation of the Square Root of 64
The square root of a number n is a number x such that \(x^2 = n\). For the number 64:
\[
\sqrt{64} = 8 \quad \text{because} \quad 8^2 = 64
\]
Rationality of the Square Root of 64
Since 8 is an integer, and all integers are rational numbers (they can be expressed as the fraction p/1 where p is the integer and 1 is a non-zero integer), the square root of 64 is rational.
Conclusion
Therefore, the square root of 64 is a rational number.

READ MORE:
Introduction
The question "Is the square root of 64 rational?" delves into the realm of number theory, focusing on the properties and classifications of numbers. To answer this, we first need to understand what rational numbers are and how square roots are defined and calculated. This introduction will guide you step by step through these concepts.
Firstly, a rational number is any number that can be expressed as the quotient of two integers, where the denominator is not zero. Examples include simple fractions like
Next, let's define the square root. The square root of a number n is a value that, when multiplied by itself, gives n. For example, the square root of 64 is a number x such that
Now, we compute the square root of 64:
\[ \sqrt{64} = 8 \]
Here, 8 is an integer, and since all integers can be expressed as a fraction of themselves over 1, 8 is a rational number.
Therefore, the square root of 64 is rational. This introduction sets the stage for a deeper exploration of the properties of rational numbers and square roots, with clear examples and logical reasoning.
Understanding Rational Numbers
To determine if the square root of 64 is rational, we need to understand what rational numbers are. Rational numbers are numbers that can be expressed as the quotient or fraction of two integers, where the numerator is an integer and the denominator is a non-zero integer.
Let's break down the key characteristics of rational numbers:
- Fractions: Any number that can be written in the form
\(\frac{p}{q}\) , where \(p\) and \(q\) are integers and \(q \neq 0\), is a rational number. Examples include\(\frac{1}{2}\) ,\(\frac{-3}{4}\) , and\(\frac{7}{1}\) . - Integers: All integers are rational numbers because any integer \(a\) can be written as
\(\frac{a}{1}\) . Examples include 1, -5, and 0. - Terminating Decimals: Decimals that come to an end, such as 0.75 (which is
\(\frac{3}{4}\) ) and 2.5 (which is\(\frac{5}{2}\) ), are rational. - Repeating Decimals: Decimals that repeat a pattern indefinitely are also rational. For example, 0.333... (which is
\(\frac{1}{3}\) ) and 0.666... (which is\(\frac{2}{3}\) ).
In summary, rational numbers include a wide variety of numbers, all of which can be expressed in fractional form with integer components. This broad category of numbers is essential for understanding why certain numbers, such as the square root of 64, can be classified as rational.
Properties of Rational Numbers
Rational numbers have several key properties that distinguish them from other types of numbers. These properties help us understand their behavior and the operations that can be performed on them.
- Closure: Rational numbers are closed under addition, subtraction, multiplication, and division (except by zero). This means that if you perform any of these operations on two rational numbers, the result will also be a rational number.
- Commutativity: Rational numbers are commutative under addition and multiplication. This means that the order in which you add or multiply two rational numbers does not affect the result. For example,
\(\frac{a}{b} + \frac{c}{d} = \frac{c}{d} + \frac{a}{b}\) and\(\frac{a}{b} \times \frac{c}{d} = \frac{c}{d} \times \frac{a}{b}\) . - Associativity: Rational numbers are associative under addition and multiplication. This means that when adding or multiplying three or more rational numbers, the grouping of the numbers does not affect the result. For example,
\((\frac{a}{b} + \frac{c}{d}) + \frac{e}{f} = \frac{a}{b} + (\frac{c}{d} + \frac{e}{f})\) and\((\frac{a}{b} \times \frac{c}{d}) \times \frac{e}{f} = \frac{a}{b} \times (\frac{c}{d} \times \frac{e}{f})\) . - Distributivity: Rational numbers follow the distributive property of multiplication over addition. This means that multiplying a sum by a number is the same as doing each multiplication separately. For example,
\(\frac{a}{b} \times (\frac{c}{d} + \frac{e}{f}) = \frac{a}{b} \times \frac{c}{d} + \frac{a}{b} \times \frac{e}{f}\) . - Density: Between any two rational numbers, there is always another rational number. This property ensures that rational numbers are densely packed on the number line.
- Equality: Two rational numbers
\(\frac{a}{b}\) and\(\frac{c}{d}\) are equal if and only if\(ad = bc\) . This cross-multiplication property helps in comparing and simplifying rational numbers.
These properties make rational numbers versatile and essential in various mathematical operations and real-world applications. Understanding these properties is crucial for recognizing the rationality of numbers like the square root of 64.
Definition and Calculation of Square Roots
Understanding the concept of square roots is fundamental to determining whether the square root of 64 is rational. The square root of a number n is a value that, when multiplied by itself, equals n. Mathematically, if x is the square root of n, then:
\[ x^2 = n \]
For example, to find the square root of 64, we need to determine the number that, when squared, equals 64. Let's break down the steps for calculating square roots:
- Identify the Perfect Square: First, check if the number is a perfect square. A perfect square is an integer that is the square of another integer. In this case, 64 is a perfect square because:
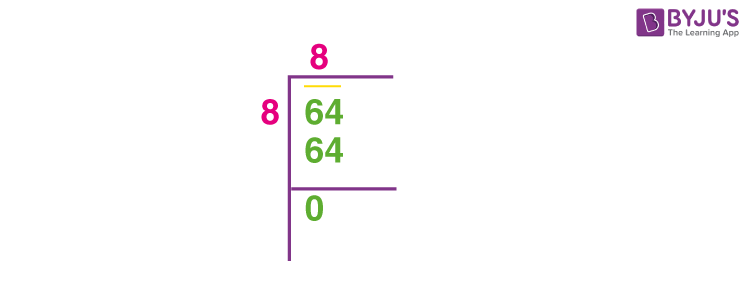
\[ 8^2 = 64 \]
- Finding the Square Root: The square root of a perfect square can be found by taking the positive integer whose square is the given number. For 64, the square root is:
\[ \sqrt{64} = 8 \]
- Verification: Verify the result by squaring the obtained value to ensure it equals the original number:
\[ 8 \times 8 = 64 \]
For non-perfect squares, other methods such as prime factorization, estimation, or using a calculator can be employed to find the square root. However, for perfect squares like 64, the process is straightforward as shown above.
In conclusion, the square root of 64 is 8, which is an integer and therefore a rational number. This straightforward calculation demonstrates the simplicity and elegance of working with perfect squares and their roots.

The Square Root of 64
The square root of a number is a value that, when multiplied by itself, gives the original number. To determine whether the square root of 64 is rational, we need to calculate the square root and examine its properties.
- Identifying the Perfect Square:
First, we recognize that 64 is a perfect square. A perfect square is an integer that is the square of another integer. In this case, 64 can be written as:
\[ 64 = 8^2 \]
- Calculating the Square Root:
The square root of 64 is the number that, when squared, equals 64. Mathematically, this is expressed as:
\[ \sqrt{64} = 8 \]
- Verification:
To verify, we can square the result to see if it equals 64:
\[ 8 \times 8 = 64 \]
Since 8 is an integer, and all integers are rational numbers (they can be expressed as the fraction
Let's summarize the steps:
- Step 1: Recognize that 64 is a perfect square.
- Step 2: Calculate the square root, which is 8.
- Step 3: Verify by squaring 8 to ensure it equals 64.
- Step 4: Conclude that since 8 is an integer, the square root of 64 is rational.
In conclusion, the square root of 64 is 8, a rational number. This example clearly shows how understanding the properties of numbers and basic arithmetic operations helps in identifying the nature of a number like the square root of 64.
Proof of Rationality for the Square Root of 64
To prove that the square root of 64 is rational, we need to demonstrate that it can be expressed as a ratio of two integers. A rational number is any number that can be written in the form
- Identify the Square Root:
The first step is to identify the square root of 64. We know that:
\[ \sqrt{64} = 8 \]
- Express as a Ratio:
Next, we express the square root of 64 as a ratio of two integers. Since 8 is an integer, we can write it as:
\[ 8 = \frac{8}{1} \]
- Verify Rationality:
To verify that 8 is a rational number, we check the definition of a rational number. The fraction \(\frac{8}{1}\) consists of two integers, 8 (numerator) and 1 (denominator), and the denominator is not zero. Therefore, 8 is a rational number.
- Conclusion:
Since the square root of 64 is 8, and 8 can be expressed as the fraction \(\frac{8}{1}\), we conclude that the square root of 64 is rational.
Let's summarize the proof:
- Step 1: Calculate the square root of 64, which is 8.
- Step 2: Express 8 as the ratio \(\frac{8}{1}\).
- Step 3: Verify that \(\frac{8}{1}\) meets the definition of a rational number.
- Step 4: Conclude that the square root of 64 is rational.
This proof clearly shows that the square root of 64 is a rational number by demonstrating it can be written as a ratio of two integers.
Examples of Rational and Irrational Numbers
Rational and irrational numbers are fundamental concepts in mathematics. Below are some examples to help understand the difference between them.
Rational Numbers
A rational number is any number that can be expressed as the quotient or fraction p/q of two integers, where p and q are integers and q is not zero. Rational numbers can be written as terminating or repeating decimals.
- Examples of rational numbers:
- \( \frac{1}{2} \) (0.5)
- \( \frac{3}{4} \) (0.75)
- 5 (which can be written as \( \frac{5}{1} \))
- \( -2 \) (which can be written as \( \frac{-2}{1} \))
- 0.333... (which is \( \frac{1}{3} \))
Irrational Numbers
An irrational number cannot be expressed as a simple fraction; it's a number that has a non-terminating and non-repeating decimal expansion. These numbers cannot be written as a ratio of two integers.
- Examples of irrational numbers:
- \( \sqrt{2} \) (approximately 1.4142135...)
- \( \pi \) (approximately 3.14159265...)
- \( e \) (approximately 2.7182818...)
- The golden ratio \( \phi \) (approximately 1.6180339...)
- \( \sqrt{3} \) (approximately 1.7320508...)
Comparison of Rational and Irrational Numbers
| Characteristic | Rational Numbers | Irrational Numbers |
|---|---|---|
| Definition | Can be expressed as a fraction of two integers | Cannot be expressed as a fraction of two integers |
| Decimal Expansion | Terminating or repeating | Non-terminating and non-repeating |
| Examples | \( \frac{1}{2}, \frac{3}{4}, 5, -2, 0.333... \) | \( \sqrt{2}, \pi, e, \phi, \sqrt{3} \) |
Understanding these differences helps in recognizing the nature of numbers we encounter in various mathematical contexts.
Comparing Rational and Irrational Numbers
To understand the differences between rational and irrational numbers, let's delve into their definitions and properties, along with examples of each type.
Rational Numbers
A rational number is any number that can be expressed as the quotient or fraction a/b of two integers, where a (the numerator) and b (the denominator) are integers and b is not zero. Rational numbers include:
- Whole numbers (e.g., 5, 12, 0)
- Integers (e.g., -3, 0, 7)
- Fractions (e.g., 1/2, 3/4, -5/6)
- Finite decimals (e.g., 0.5, -2.75)
- Repeating decimals (e.g., 0.333..., 1.666...)
For example, the number 8, which is the square root of 64, is a rational number because it can be expressed as the fraction 8/1.
Irrational Numbers
An irrational number cannot be expressed as a simple fraction; it is a non-repeating, non-terminating decimal. Some common examples include:
- The square root of any non-perfect square (e.g., √2, √3)
- Mathematical constants (e.g., π, e)
For instance, the square root of 2 (approximately 1.41421356...) is irrational because it cannot be precisely written as a fraction.
Comparison Table
| Aspect | Rational Numbers | Irrational Numbers |
|---|---|---|
| Definition | Can be expressed as a fraction a/b where a and b are integers and b ≠ 0 | Cannot be expressed as a fraction; non-terminating and non-repeating decimal |
| Examples | 1/2, -3, 4.5, 8 | π, √2, e |
| Decimal Expansion | Finite or repeating | Infinite and non-repeating |
In summary, while rational numbers are those that can be neatly expressed as fractions, irrational numbers defy such simple expression. Understanding the properties of both helps in grasping the full spectrum of real numbers.
Tìm hiểu về căn bậc hai của 64 và tại sao nó là một số hữu tỉ. Video giải thích chi tiết và dễ hiểu để thu hút người xem.
Căn Bậc Hai của 64
READ MORE:
Hướng dẫn chi tiết về cách đánh giá căn bậc hai của một số hữu tỉ là số chính phương. Ví dụ với căn(64/196), giúp người xem hiểu rõ hơn về khái niệm này.
Đánh giá căn bậc hai của một số hữu tỉ là số chính phương ví dụ 8, căn(64/196)