Topic what is the square root of negative 64: Understanding the square root of negative 64 opens the door to the fascinating world of imaginary numbers. This article explores the concept of imaginary units, explains the step-by-step process to calculate the square root of negative numbers, and highlights the importance of these numbers in advanced mathematics. Join us as we unravel this intriguing mathematical concept.
Table of Content
- Understanding the Square Root of Negative 64
- Introduction to Square Roots of Negative Numbers
- Understanding Imaginary Numbers
- Basic Concept of Imaginary Unit (i)
- Mathematical Definition of Imaginary Numbers
- Calculating the Square Root of Negative 64
- Step-by-Step Solution
- Properties of Imaginary Numbers
- Applications of Imaginary Numbers
- Complex Numbers and Their Components
- Real and Imaginary Parts of Complex Numbers
- Examples and Exercises
- Common Misconceptions
- Historical Context and Development
- Advanced Topics in Complex Numbers
- Conclusion and Summary
- YOUTUBE:
Understanding the Square Root of Negative 64
The square root of a negative number introduces the concept of imaginary numbers, which are a fundamental part of complex numbers in mathematics.
Imaginary Numbers
An imaginary number is defined as the square root of a negative number. The unit imaginary number is denoted as i, where:
\[ i = \sqrt{-1} \]
Calculation of the Square Root of -64
To find the square root of -64, we can express it in terms of i:
\[ \sqrt{-64} = \sqrt{64 \times -1} = \sqrt{64} \times \sqrt{-1} = 8i \]
Steps to Solve
- Recognize that the negative sign under the square root indicates the need for an imaginary number.
- Separate the negative sign and the positive number: \(\sqrt{-64} = \sqrt{64} \times \sqrt{-1}\).
- Compute the square root of the positive number: \(\sqrt{64} = 8\).
- Combine the results with the imaginary unit: \(8 \times i = 8i\).
Conclusion
The square root of -64 is expressed as:
\[ \sqrt{-64} = 8i \]
This demonstrates the use of imaginary numbers in solving the square roots of negative values.
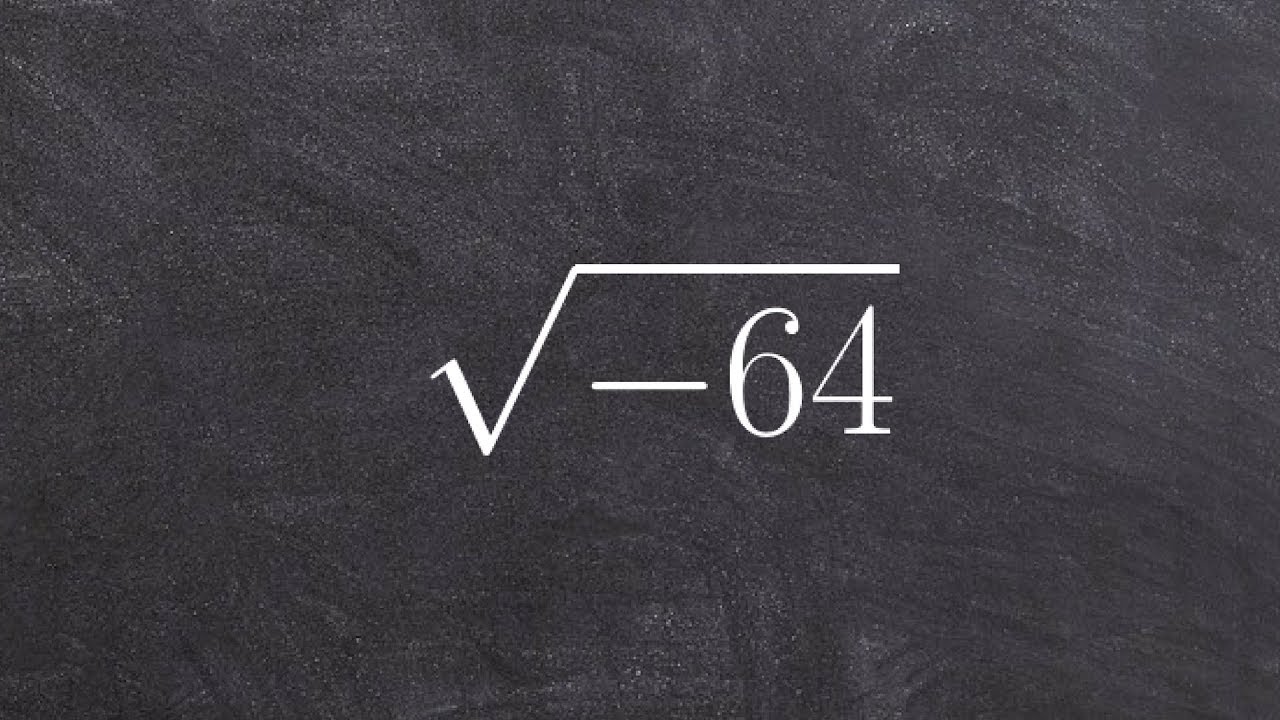
READ MORE:
Introduction to Square Roots of Negative Numbers
Square roots of negative numbers introduce an essential concept in mathematics: imaginary numbers. Unlike positive numbers, negative numbers do not have real square roots because no real number squared gives a negative result. This is where imaginary numbers come into play.
Imaginary numbers are defined using the imaginary unit \( i \), which is the square root of -1:
\[ i = \sqrt{-1} \]
Using \( i \), we can express the square root of any negative number. For example, to find the square root of -64, we follow these steps:
- Identify the negative number inside the square root: \(\sqrt{-64}\).
- Rewrite the expression using the property of square roots: \(\sqrt{-64} = \sqrt{64 \times -1}\).
- Separate the square root into its components: \(\sqrt{64} \times \sqrt{-1}\).
- Calculate the square root of the positive part: \(\sqrt{64} = 8\).
- Combine the results with the imaginary unit \( i \): \(8 \times i = 8i\).
Therefore, the square root of -64 is \( 8i \). This concept is crucial for understanding complex numbers, which have applications in various fields such as engineering, physics, and applied mathematics.
Understanding Imaginary Numbers
Imaginary numbers arise when we take the square root of negative numbers. The fundamental unit of imaginary numbers is \( i \), defined as \( \sqrt{-1} \). This concept is crucial in extending the real number system to the complex number system, allowing us to solve equations that have no real solutions.
For example, the square root of -64 can be expressed using \( i \) as follows:
- The square root of -64 is \( \pm 8i \).
- Here, \( 8i \) and \( -8i \) are called the imaginary roots of -64.
Imaginary numbers are used in various fields such as engineering, physics, and applied mathematics to solve complex problems. By understanding the basics of imaginary numbers, we can better appreciate their role in advanced mathematical concepts and real-world applications.
Basic Concept of Imaginary Unit (i)
The imaginary unit, denoted as i, is a fundamental concept in mathematics, particularly in the field of complex numbers. It is defined as the square root of -1, a number which does not have a real counterpart. The introduction of i allows for the extension of the real number system to include solutions to equations that would otherwise have no real solutions.
Key properties of the imaginary unit i include:
- i is defined by the equation i² = -1.
- From this definition, it follows that i = √-1.
- The powers of i cycle in a pattern:
- i¹ = i
- i² = -1
- i³ = -i
- i⁴ = 1
This cyclical nature is crucial in various mathematical computations and simplifies the manipulation of powers of i.
To illustrate the usage of i, let's consider the equation x² + 1 = 0. Solving for x:
- Move 1 to the right side of the equation: x² = -1.
- Take the square root of both sides: x = ±√-1.
- Using the definition of i, this can be rewritten as x = ±i.
Thus, the solutions to the equation x² + 1 = 0 are x = i and x = -i, demonstrating how i provides solutions to equations involving negative square roots.
Mathematical Definition of Imaginary Numbers
Imaginary numbers are numbers that can be written in the form of a real number multiplied by the imaginary unit i, where i is defined as \( \sqrt{-1} \). The concept of imaginary numbers extends the real number system to include solutions to equations that do not have real solutions.
The imaginary unit i has the following defining property:
- \( i^2 = -1 \)
This property is fundamental to understanding imaginary numbers and their role in mathematics. Let's break down the steps to define and utilize imaginary numbers:
- Start with the equation that has no real solution, such as \( x^2 + 1 = 0 \).
- Rewrite the equation to isolate the term with the variable: \( x^2 = -1 \).
- Take the square root of both sides: \( x = \pm \sqrt{-1} \).
- Introduce the imaginary unit i such that \( i = \sqrt{-1} \), so \( x = \pm i \).
Thus, the solutions to the equation \( x^2 + 1 = 0 \) are \( x = i \) and \( x = -i \).
Imaginary numbers can be combined with real numbers to form complex numbers, which are expressed in the form \( a + bi \), where \( a \) and \( b \) are real numbers. Here, \( a \) is the real part and \( bi \) is the imaginary part.
To illustrate with an example, consider the square root of -64:
- Rewrite \( \sqrt{-64} \) as \( \sqrt{64 \cdot -1} \).
- Separate the square roots: \( \sqrt{64} \cdot \sqrt{-1} \).
- Since \( \sqrt{64} = 8 \) and \( \sqrt{-1} = i \), we have \( 8i \).
Therefore, \( \sqrt{-64} = 8i \).
This example demonstrates how imaginary numbers are used to extend the concept of square roots to negative numbers, providing a consistent and useful mathematical framework.

Calculating the Square Root of Negative 64
Calculating the square root of a negative number involves understanding the concept of imaginary numbers. Here, we will go through the step-by-step process to find the square root of -64.
The square root of -64 can be calculated as follows:
- Identify the negative number inside the square root: \( \sqrt{-64} \).
- Rewrite the expression to separate the negative part: \( \sqrt{-64} = \sqrt{64 \cdot -1} \).
- Apply the property of square roots which allows us to separate the product of two numbers under the square root: \( \sqrt{64 \cdot -1} = \sqrt{64} \cdot \sqrt{-1} \).
- Recognize that \( \sqrt{64} \) is a real number. Since \( 64 \) is a perfect square, \( \sqrt{64} = 8 \).
- Understand that \( \sqrt{-1} \) is defined as the imaginary unit \( i \), where \( i = \sqrt{-1} \).
- Combine the results to express the final answer: \( \sqrt{64} \cdot \sqrt{-1} = 8 \cdot i = 8i \).
Therefore, the square root of -64 is \( 8i \).
Here is a summary table of the steps:
| Step | Explanation |
|---|---|
| 1 | Identify the negative number inside the square root: \( \sqrt{-64} \). |
| 2 | Rewrite as a product: \( \sqrt{64 \cdot -1} \). |
| 3 | Separate the square roots: \( \sqrt{64} \cdot \sqrt{-1} \). |
| 4 | Calculate \( \sqrt{64} \): \( 8 \). |
| 5 | Recognize \( \sqrt{-1} \) as \( i \). |
| 6 | Combine to get the final result: \( 8i \). |
This method showcases the utility of imaginary numbers in handling square roots of negative values, making them an essential tool in advanced mathematics.
Step-by-Step Solution
To calculate the square root of -64, we will use the concept of imaginary numbers. Here is a detailed, step-by-step solution:
- Start with the given expression:
\( \sqrt{-64} \)
- Rewrite the expression to separate the negative part:
\( \sqrt{-64} = \sqrt{64 \cdot -1} \)
- Apply the property of square roots that allows us to separate the product of two numbers under the square root:
\( \sqrt{64 \cdot -1} = \sqrt{64} \cdot \sqrt{-1} \)
- Calculate the square root of the positive number 64:
\( \sqrt{64} = 8 \)
- Recognize that the square root of -1 is the imaginary unit \( i \):
\( \sqrt{-1} = i \)
- Combine the results to express the final answer:
\( \sqrt{64} \cdot \sqrt{-1} = 8 \cdot i = 8i \)
Therefore, the square root of -64 is \( 8i \).
For clarity, here is a summary table of the steps:
| Step | Explanation |
|---|---|
| 1 | Identify the negative number inside the square root: \( \sqrt{-64} \). |
| 2 | Rewrite as a product: \( \sqrt{64 \cdot -1} \). |
| 3 | Separate the square roots: \( \sqrt{64} \cdot \sqrt{-1} \). |
| 4 | Calculate \( \sqrt{64} \): \( 8 \). |
| 5 | Recognize \( \sqrt{-1} \) as \( i \). |
| 6 | Combine to get the final result: \( 8i \). |
This step-by-step approach demonstrates how imaginary numbers are used to calculate the square root of negative values, providing a clear and logical method for solving such problems.
Properties of Imaginary Numbers
Imaginary numbers extend the real number system and have unique properties that are essential for solving a wide range of mathematical problems. Here are the key properties of imaginary numbers:
- Imaginary Unit: The imaginary unit is denoted as i, and it is defined by the property:
\( i^2 = -1 \)
- Definition: An imaginary number is a multiple of the imaginary unit i. For example, \( bi \) where \( b \) is a real number, is an imaginary number.
- Complex Numbers: Combining real numbers with imaginary numbers forms complex numbers, which are written as \( a + bi \), where \( a \) and \( b \) are real numbers.
The imaginary unit i has cyclical powers, which repeat every four steps:
- \( i^1 = i \)
- \( i^2 = -1 \)
- \( i^3 = -i \)
- \( i^4 = 1 \)
This cycle repeats, meaning:
- \( i^5 = i \)
- \( i^6 = -1 \)
- \( i^7 = -i \)
- \( i^8 = 1 \)
These cyclical properties help in simplifying complex expressions involving powers of i.
Another important property is the addition and subtraction of imaginary numbers, which is straightforward:
- \( (a + bi) + (c + di) = (a + c) + (b + d)i \)
- \( (a + bi) - (c + di) = (a - c) + (b - d)i \)
Multiplication of imaginary numbers follows the distributive property:
\( (a + bi)(c + di) = ac + adi + bci + bdi^2 \)
Since \( i^2 = -1 \), the expression simplifies to:
\( (a + bi)(c + di) = ac + adi + bci - bd \)
Which can be further simplified to:
\( (ac - bd) + (ad + bc)i \)
Division of imaginary numbers involves rationalizing the denominator:
- Multiply the numerator and the denominator by the conjugate of the denominator.
- For example, to divide \( \frac{a + bi}{c + di} \), multiply by the conjugate \( c - di \):
- \( \frac{(a + bi)(c - di)}{(c + di)(c - di)} \)
- This simplifies using the properties above:
- \( \frac{(ac + bd) + (bc - ad)i}{c^2 + d^2} \)
Understanding these properties is crucial for working with and manipulating imaginary and complex numbers in various mathematical contexts.
Applications of Imaginary Numbers
Imaginary numbers, when combined with real numbers to form complex numbers, have a wide range of applications in various fields. Here are some of the key areas where imaginary numbers are utilized:
- Electrical Engineering:
In electrical engineering, complex numbers are used to analyze AC circuits. Impedance, which combines resistance and reactance, is represented as a complex number \( Z = R + jX \), where \( j \) (equivalent to \( i \) in mathematics) represents the imaginary unit.
- Signal Processing:
Imaginary numbers are crucial in signal processing, particularly in Fourier transforms. The Fourier transform converts time-domain signals into frequency-domain representations, using complex numbers to encode amplitude and phase information.
- Control Systems:
Control systems engineering relies on complex numbers to design and analyze system stability and response. The poles and zeros of transfer functions are often complex, influencing system behavior.
- Quantum Mechanics:
In quantum mechanics, complex numbers are fundamental in describing the state of a quantum system. The Schrödinger equation, which governs the evolution of quantum states, utilizes complex-valued wave functions.
- Fluid Dynamics:
Complex numbers are used in fluid dynamics to simplify the analysis of fluid flow, particularly in potential flow theory. The complex potential function represents the flow, making it easier to solve flow equations.
- Electromagnetic Theory:
Electromagnetic waves are described using complex numbers to represent the electric and magnetic fields. Maxwell's equations, which form the foundation of electromagnetism, often employ complex notation for simplicity.
Here are some specific examples of how imaginary numbers are applied:
- AC Circuit Analysis:
- Representing impedance: \( Z = R + jX \)
- Calculating total impedance in series and parallel circuits
- Analyzing voltage and current phasors
- Fourier Transform:
- Transforming a signal: \( F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-j\omega t} dt \)
- Interpreting frequency components of signals
- Quantum Mechanics:
- Wave function: \( \Psi(x, t) = Ae^{i(kx - \omega t)} \)
- Probability density: \( |\Psi|^2 \)
Imaginary numbers, through their role in complex numbers, provide powerful tools for modeling, analyzing, and solving problems across various scientific and engineering disciplines. Their applications are essential for advancing technology and understanding the natural world.

Complex Numbers and Their Components
Complex numbers are an extension of the real number system and are composed of two parts: a real part and an imaginary part. A complex number is generally written in the form \( a + bi \), where \( a \) and \( b \) are real numbers, and \( i \) is the imaginary unit defined by \( i^2 = -1 \).
Let's break down the components of a complex number:
- Real Part:
The real part of a complex number \( a + bi \) is \( a \). This component lies along the horizontal axis of the complex plane.
- Imaginary Part:
The imaginary part of a complex number \( a + bi \) is \( b \). This component lies along the vertical axis of the complex plane and is multiplied by the imaginary unit \( i \).
In the complex plane, also known as the Argand plane, complex numbers are represented as points or vectors. The horizontal axis represents the real part, while the vertical axis represents the imaginary part.
Here is a visual representation of a complex number \( a + bi \) in the complex plane:
| Real Axis | Imaginary Axis |
| Real Part \( a \) | Imaginary Part \( bi \) |
Complex numbers can be added, subtracted, multiplied, and divided. Here are the basic operations:
- Addition:
To add two complex numbers \( (a + bi) \) and \( (c + di) \), add their real parts and their imaginary parts separately:
\( (a + bi) + (c + di) = (a + c) + (b + d)i \)
- Subtraction:
To subtract two complex numbers \( (a + bi) \) and \( (c + di) \), subtract their real parts and their imaginary parts separately:
\( (a + bi) - (c + di) = (a - c) + (b - d)i \)
- Multiplication:
To multiply two complex numbers \( (a + bi) \) and \( (c + di) \), use the distributive property:
\( (a + bi)(c + di) = ac + adi + bci + bdi^2 \)
Since \( i^2 = -1 \), this simplifies to:
\( (ac - bd) + (ad + bc)i \)
- Division:
To divide two complex numbers \( \frac{a + bi}{c + di} \), multiply the numerator and the denominator by the conjugate of the denominator \( (c - di) \):
\( \frac{(a + bi)(c - di)}{(c + di)(c - di)} = \frac{(ac + bd) + (bc - ad)i}{c^2 + d^2} \)
Complex numbers are essential in various fields, including engineering, physics, and mathematics, providing a powerful tool for solving equations and representing phenomena that cannot be described using only real numbers.
Real and Imaginary Parts of Complex Numbers
Complex numbers consist of two distinct parts: the real part and the imaginary part. These components allow complex numbers to extend the real number system and handle a wider range of mathematical problems.
A complex number is typically written in the form \( a + bi \), where:
- \( a \) is the real part.
- \( b \) is the imaginary part and \( i \) is the imaginary unit, defined by \( i^2 = -1 \).
To better understand these parts, let's break down a complex number:
- Real Part:
The real part of the complex number \( a + bi \) is \( a \). It represents the component that lies on the real axis in the complex plane. For example, in the complex number \( 3 + 4i \), the real part is \( 3 \).
- Imaginary Part:
The imaginary part of the complex number \( a + bi \) is \( b \). This part is multiplied by the imaginary unit \( i \) and lies on the imaginary axis in the complex plane. For instance, in the complex number \( 3 + 4i \), the imaginary part is \( 4i \).
Here is a visual representation of a complex number \( a + bi \) in the complex plane:
| Axis | Component |
|---|---|
| Real Axis | Real Part \( a \) |
| Imaginary Axis | Imaginary Part \( bi \) |
Operations involving complex numbers take into account both the real and imaginary parts:
- Addition and Subtraction:
To add or subtract complex numbers, combine their real parts and their imaginary parts separately.
\( (a + bi) + (c + di) = (a + c) + (b + d)i \)
\( (a + bi) - (c + di) = (a - c) + (b - d)i \)
- Multiplication:
Multiply complex numbers using the distributive property, remembering that \( i^2 = -1 \).
\( (a + bi)(c + di) = ac + adi + bci + bdi^2 \)
\( = ac + adi + bci - bd \)
\( = (ac - bd) + (ad + bc)i \)
- Division:
Divide complex numbers by multiplying the numerator and the denominator by the conjugate of the denominator.
\( \frac{a + bi}{c + di} = \frac{(a + bi)(c - di)}{(c + di)(c - di)} \)
\( = \frac{(ac + bd) + (bc - ad)i}{c^2 + d^2} \)
Understanding the real and imaginary parts of complex numbers is essential for working with complex equations, performing arithmetic operations, and applying complex numbers in various scientific and engineering fields.
Examples and Exercises
Understanding the square root of negative numbers and working with imaginary numbers can be challenging. Here are some examples and exercises to help solidify these concepts.
Example 1: Square Root of Negative 64
To find the square root of -64, we use the imaginary unit \( i \), where \( i^2 = -1 \).
- First, express -64 as the product of -1 and 64:
\( -64 = -1 \times 64 \)
- Next, take the square root of both parts:
\( \sqrt{-64} = \sqrt{-1 \times 64} = \sqrt{-1} \times \sqrt{64} \)
- Since \( \sqrt{-1} = i \) and \( \sqrt{64} = 8 \):
\( \sqrt{-64} = 8i \)
Example 2: Addition of Complex Numbers
Add \( (3 + 4i) \) and \( (1 + 2i) \):
- Add the real parts: \( 3 + 1 = 4 \)
- Add the imaginary parts: \( 4i + 2i = 6i \)
- Combine the results: \( (3 + 4i) + (1 + 2i) = 4 + 6i \)
Example 3: Multiplication of Complex Numbers
Multiply \( (2 + 3i) \) and \( (1 + 4i) \):
- Distribute the terms: \( (2 + 3i)(1 + 4i) = 2 \times 1 + 2 \times 4i + 3i \times 1 + 3i \times 4i \)
- Calculate each part:
- Real part: \( 2 \times 1 = 2 \)
- Imaginary part: \( 2 \times 4i = 8i \) and \( 3i \times 1 = 3i \)
- Combined imaginary part: \( 8i + 3i = 11i \)
- Imaginary unit squared: \( 3i \times 4i = 12i^2 = 12(-1) = -12 \)
- Combine the results: \( 2 + 11i - 12 = -10 + 11i \)
Exercises
Try solving these exercises to practice your understanding of complex numbers:
- Find the square root of -25.
- Subtract \( (5 + 7i) \) from \( (8 + 3i) \).
- Multiply \( (4 + 2i) \) and \( (3 + 5i) \).
- Divide \( (6 + 8i) \) by \( (2 + 4i) \).
- Find the magnitude and argument of the complex number \( 1 + i \).
These examples and exercises will help you become more comfortable with imaginary and complex numbers, enhancing your problem-solving skills in this area.
Common Misconceptions
Understanding imaginary numbers and their applications can be challenging, leading to several common misconceptions. Here, we address some of the most frequent misunderstandings and clarify the correct concepts.
Misconception 1: Imaginary Numbers Are Not Real
While the term "imaginary" might suggest that these numbers are not real or do not exist, this is not true. Imaginary numbers are just as valid as real numbers within the realm of mathematics. They provide a way to extend the number system to solve equations that do not have solutions within the real numbers alone.
Misconception 2: The Square Root of a Negative Number Is Undefined
In the context of real numbers, the square root of a negative number is indeed undefined. However, when we extend the number system to include imaginary numbers, we can define the square root of negative numbers. For example, the square root of -64 is \( 8i \), where \( i \) is the imaginary unit.
Misconception 3: \( i \) Is Just a Variable
Some may mistakenly treat the imaginary unit \( i \) as if it were a regular variable. However, \( i \) is a specific constant defined by the property \( i^2 = -1 \). This unique property is what allows us to work with imaginary and complex numbers.
Misconception 4: Complex Numbers Cannot Be Compared
While it is true that there is no natural ordering of complex numbers as there is with real numbers, complex numbers can still be compared in terms of their magnitudes (or absolute values). The magnitude of a complex number \( a + bi \) is given by \( \sqrt{a^2 + b^2} \).
Misconception 5: Imaginary Numbers Have No Practical Applications
Contrary to this belief, imaginary numbers have numerous practical applications in engineering, physics, and other sciences. They are used in electrical engineering, signal processing, quantum mechanics, fluid dynamics, and more. These applications demonstrate the utility and importance of imaginary numbers in solving real-world problems.
Misconception 6: The Sum of Two Imaginary Numbers Is Always Imaginary
When adding two imaginary numbers, the result can sometimes be a real number. For example:
\( (3i) + (-3i) = 0 \)
Here, the imaginary parts cancel out, leaving a real number.
Misconception 7: Complex Numbers Are Difficult to Work With
While they may seem complex initially, with practice, operations involving complex numbers become straightforward. Understanding their properties and the basic arithmetic rules can simplify many mathematical problems.
By addressing and correcting these common misconceptions, we can better appreciate the role and significance of imaginary and complex numbers in mathematics and their various applications.

Historical Context and Development
The concept of square roots, particularly of negative numbers, has a rich historical background. The earliest known methods for calculating square roots date back to ancient civilizations. For instance, the Babylonian clay tablet YBC 7289, created between 1800 BC and 1600 BC, demonstrates the use of a base-60 system to approximate the square root of 2.
In ancient Egypt, the Rhind Mathematical Papyrus from around 1650 BC shows that the Egyptians used an inverse proportion method to extract square roots. Similarly, ancient Indian texts such as the Sulba Sutras, dated around 800-500 BC, provided detailed methods for finding square roots. Aryabhata, a prominent Indian mathematician from the 5th century AD, offered a systematic approach for calculating square roots in his work Aryabhatiya.
The Greeks also made significant contributions to the understanding of square roots. The Pythagorean school recognized that the square roots of non-square positive integers are irrational numbers, a concept attributed to Theaetetus and formalized in Euclid's Elements.
The notion of imaginary numbers, which includes the square root of negative numbers, emerged much later. During the Renaissance, mathematicians like Gerolamo Cardano explored solutions to cubic equations, which sometimes involved the square roots of negative numbers. This exploration led to the formal introduction of imaginary numbers.
In the 16th century, Rafael Bombelli provided a systematic treatment of complex numbers, including the imaginary unit \(i\), where \(i\) is defined as \(\sqrt{-1}\). This marked a significant development in the field of mathematics, allowing for the expansion of solutions to polynomial equations.
Over time, the study of complex numbers, which combine real and imaginary parts, evolved. The standard form of a complex number is expressed as \(a + bi\), where \(a\) and \(b\) are real numbers. This framework has profound implications in various fields, including engineering, physics, and applied mathematics.
In summary, the historical development of square roots of negative numbers spans from ancient methods of extracting square roots to the Renaissance's conceptualization of imaginary numbers. These advancements have laid the foundation for modern complex number theory, significantly impacting mathematical and scientific progress.
Advanced Topics in Complex Numbers
Complex numbers, represented as \( a + bi \) where \( a \) and \( b \) are real numbers and \( i \) is the imaginary unit (\( i^2 = -1 \)), have a wide array of advanced applications and properties. This section delves into some of these advanced topics, providing a comprehensive understanding of their significance and uses.
1. Complex Conjugates
The complex conjugate of a complex number \( a + bi \) is \( a - bi \). Complex conjugates have important properties and are used in various calculations such as rationalizing denominators.
- For any complex number \( z = a + bi \), its conjugate is \( \overline{z} = a - bi \).
- The product of a complex number and its conjugate is always a non-negative real number: \((a + bi)(a - bi) = a^2 + b^2\).
2. Polar and Exponential Forms
Complex numbers can be represented in polar form as \( r(\cos \theta + i \sin \theta) \) or in exponential form using Euler's formula: \( re^{i\theta} \).
- The magnitude \( r \) is given by \( r = \sqrt{a^2 + b^2} \).
- The angle \( \theta \) (or argument) is \( \theta = \tan^{-1}\left(\frac{b}{a}\right) \).
These forms are particularly useful for multiplying and dividing complex numbers, as well as for finding powers and roots of complex numbers.
3. Multiplication and Division in Polar Form
Multiplication and division of complex numbers are simplified using their polar forms:
- Multiplication: \( z_1 \cdot z_2 = r_1 r_2 e^{i(\theta_1 + \theta_2)} \)
- Division: \( \frac{z_1}{z_2} = \frac{r_1}{r_2} e^{i(\theta_1 - \theta_2)} \)
4. Complex Roots and De Moivre's Theorem
De Moivre's Theorem provides a way to compute powers and roots of complex numbers:
\((re^{i\theta})^n = r^n e^{in\theta}\)
To find the \( n \)th roots of a complex number \( re^{i\theta} \):
\( \sqrt[n]{re^{i\theta}} = \sqrt[n]{r} e^{i(\theta + 2k\pi)/n} \) for \( k = 0, 1, \ldots, n-1 \)
5. Applications of Complex Numbers
Complex numbers have numerous applications in various fields:
- Electrical Engineering: Used in the analysis of AC circuits and signal processing.
- Fluid Dynamics: Describing potential flow in fluids.
- Quantum Physics: Representing wave functions and probability amplitudes.
- Control Theory: Stability analysis of systems using the complex plane.
6. Julia Sets and Mandelbrot Sets
In fractal geometry, complex numbers are used to generate Julia sets and the Mandelbrot set, which are intricate and infinitely detailed mathematical structures.
These sets are generated by iterating complex functions and are known for their stunning visual patterns and complex boundaries.
Understanding these advanced topics provides a deeper appreciation of the versatility and power of complex numbers in both theoretical and applied mathematics.
Conclusion and Summary
The square root of negative numbers opens the door to the fascinating world of complex numbers, expanding our understanding of mathematics beyond real numbers. The specific case of the square root of -64, which is expressed as \(8i\), illustrates how the imaginary unit \(i\) (\(\sqrt{-1}\)) allows us to handle and solve equations involving negative square roots.
Throughout this guide, we've explored various aspects of imaginary and complex numbers:
- Imaginary numbers, where the square of the imaginary unit \(i\) equals -1.
- The process of calculating the square root of negative numbers using the imaginary unit.
- The concept of complex numbers, which combine real and imaginary parts.
- Properties and operations involving complex numbers, such as addition, subtraction, multiplication, and division.
- The historical development of imaginary numbers and their acceptance in the mathematical community.
- Advanced topics such as complex plane representation, polar form, and Euler's formula.
By understanding these concepts, we gain powerful tools for solving a broader range of mathematical problems, particularly in fields such as engineering, physics, and applied mathematics. Imaginary and complex numbers not only provide solutions to previously unsolvable equations but also offer deeper insights into the nature of numbers and their applications.
In summary, the journey through the square root of -64 and the realm of complex numbers highlights the importance of expanding our mathematical frameworks to embrace new ideas and solve complex problems. As we continue to explore and apply these concepts, we unlock new potential in both theoretical and practical domains.
Làm Thế Nào Để Đơn Giản Hóa Căn Bậc Hai Của Số Âm: sqrt(-64)
READ MORE:
Đại số 2 - Đơn giản hóa căn bậc hai âm bằng đơn vị ảo i, sqrt(-64)