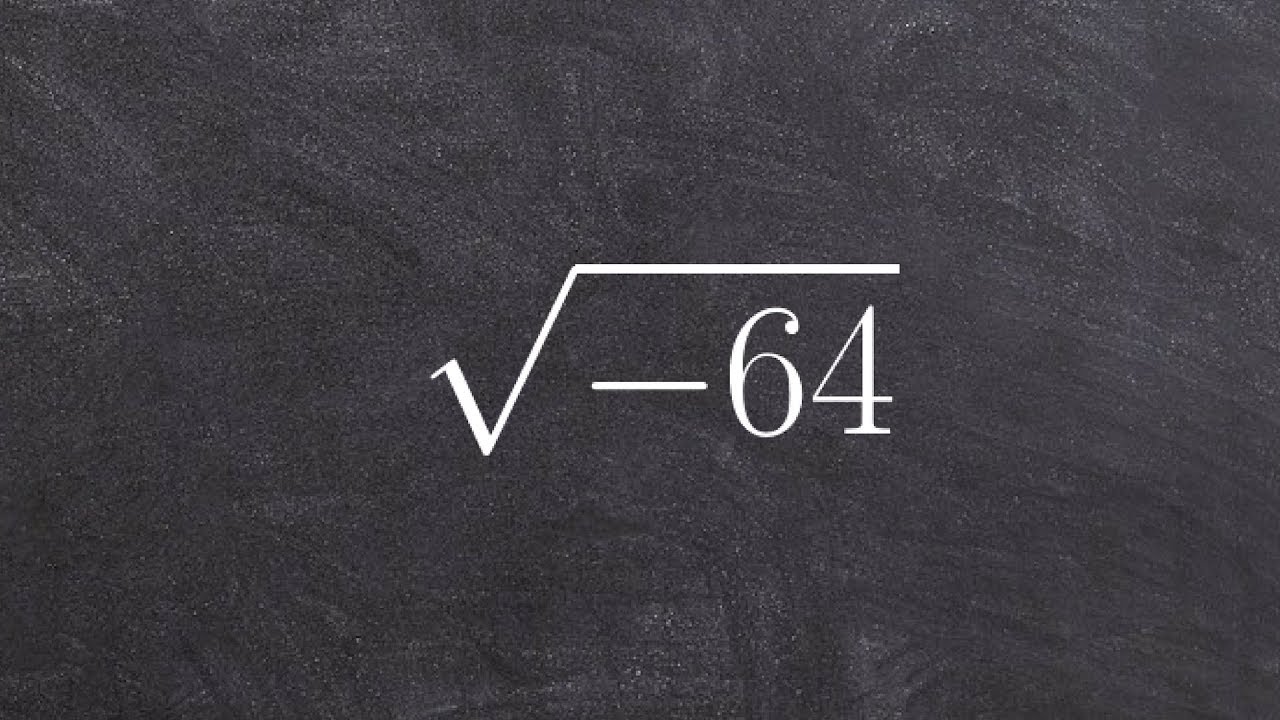Topic what is the square root of 64: Understanding the square root of 64 is essential for both basic and advanced mathematics. In this article, we will explore the definition, calculation methods, and practical applications of the square root of 64, making the concept clear and accessible for learners and enthusiasts alike.
Table of Content
- Understanding the Square Root of 64
- Introduction to Square Roots
- Definition of Square Root
- Understanding the Square Root of 64
- Mathematical Representation
- Verification of Square Roots
- Methods to Calculate Square Roots
- Prime Factorization
- Using a Calculator
- Estimation and Averaging Techniques
- Applications of Square Roots
- In Mathematics
- In Real Life
- Common Questions About Square Roots
- YOUTUBE:
Understanding the Square Root of 64
The square root of a number is a value that, when multiplied by itself, gives the original number. In this case, we are looking for the square root of 64.
Mathematical Definition
The square root of 64, denoted as √64 or \sqrt{64} in Mathjax, is the number that satisfies the equation:
\[
x^2 = 64
\]
Solving for \(x\), we find:
\[
x = \sqrt{64} = 8
\]
Positive and Negative Roots
While the principal square root of 64 is 8, it is important to note that there are two solutions to the equation \(x^2 = 64\):
- Positive root: \(x = 8\)
- Negative root: \(x = -8\)
Thus, both \(8\) and \(-8\) are square roots of 64.
Verification
To verify, we can calculate:
-
For \(8\):
\[
8 \times 8 = 64
\] -
For \(-8\):
\[
(-8) \times (-8) = 64
\]
Square Root Calculation Methods
There are several methods to find the square root of a number:
-
Prime Factorization
Prime factorize 64:
\[
64 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 = 2^6
\]Taking the square root:
\[
\sqrt{64} = \sqrt{2^6} = 2^{6/2} = 2^3 = 8
\] -
Using a Calculator
Simply inputting 64 into a calculator and pressing the square root function will yield 8.
-
Estimation and Averaging
If you start with an estimate close to 8, you can use iterative methods to refine the estimate to 8.
Conclusion
The square root of 64 is a fundamental concept in mathematics, and the principal square root is 8. Understanding both the positive and negative roots and the methods to calculate them provides a comprehensive view of this basic mathematical operation.

READ MORE:
Introduction to Square Roots
The concept of square roots is fundamental in mathematics. A square root of a number is a value that, when multiplied by itself, results in the original number. The square root is denoted by the radical symbol (√) or expressed using exponentiation as the power of 1/2.
For example:
\[
\sqrt{a} = a^{1/2}
\]
Key points about square roots include:
- Every positive number has two square roots: one positive and one negative.
- The principal square root is the non-negative root, commonly referred to when discussing square roots.
- Zero has one square root, which is 0.
- Negative numbers do not have real square roots, but they have complex square roots.
Let's take a closer look at some properties and examples:
Properties:
-
Non-negativity: The square root of a non-negative number is also non-negative.
-
Multiplicative Property: The square root of a product is equal to the product of the square roots of the factors.
\[
\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}
\] -
Quotient Property: The square root of a quotient is equal to the quotient of the square roots.
\[
\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}
\]
Examples:
-
The square root of 9 is 3, since \(3 \times 3 = 9\).
-
The square root of 25 is 5, since \(5 \times 5 = 25\).
-
The square root of 64 is 8, since \(8 \times 8 = 64\).
Understanding square roots is essential for solving equations, simplifying expressions, and working with various mathematical concepts. As we delve deeper into specific examples, such as the square root of 64, we will see how these principles are applied.
Definition of Square Root
The square root of a number is a value that, when multiplied by itself, gives the original number. It is one of the fundamental concepts in mathematics and is denoted by the radical symbol
For a given non-negative number \(a\), the square root of \(a\) is a number \(x\) such that:
In mathematical notation, the principal (non-negative) square root of \(a\) is written as
Square roots can also be negative because the product of two negative numbers is positive. Therefore, for any positive number \(a\), there are two square roots:
- The positive square root,
\(\sqrt{a}\) - The negative square root,
\(-\sqrt{a}\)
Using 64 as an example:
- The positive square root of 64 is
\(\sqrt{64} = 8\) - The negative square root of 64 is
\(-\sqrt{64} = -8\)
Thus, both 8 and -8 are square roots of 64.
Understanding the Square Root of 64
The square root of 64 is a value that, when multiplied by itself, equals 64. To understand this concept better, let's break it down step by step.
Step 1: Identify the number
The number we are working with is 64.
Step 2: Determine the square root
We need to find a number \( x \) such that \( x^2 = 64 \). This means we are looking for a number that, when multiplied by itself, equals 64.
Step 3: Calculation
The number that satisfies this condition is 8, because:
Therefore, the positive square root of 64 is 8.
Step 4: Considering negative roots
It is important to remember that square roots can also be negative because the product of two negative numbers is positive. Thus:
Therefore, the negative square root of 64 is -8.
Summary
- The positive square root of 64 is
\(\sqrt{64} = 8\) . - The negative square root of 64 is
\(-\sqrt{64} = -8\) .
Both 8 and -8 are valid square roots of 64, but in most cases, when we refer to the square root, we mean the principal (positive) square root, which is 8.
Mathematical Representation
The square root of a number \( x \) is a value that, when multiplied by itself, gives \( x \). Mathematically, this is represented as:
\[ \sqrt{x} = y \implies y^2 = x \]
For the number 64, the square root is represented as:
\[ \sqrt{64} = 8 \]
This is because:
\[ 8 \times 8 = 64 \]
Thus, we can say that \( \sqrt{64} = 8 \).
The square root function, \( \sqrt{x} \), typically returns the principal (non-negative) square root. Therefore:
\[ \sqrt{64} = 8 \]
However, it's important to note that both 8 and -8 squared give 64, i.e.,
\[ 8^2 = 64 \text{ and } (-8)^2 = 64 \]
But by convention, the square root function returns only the positive root:
\[ \sqrt{64} = 8 \]
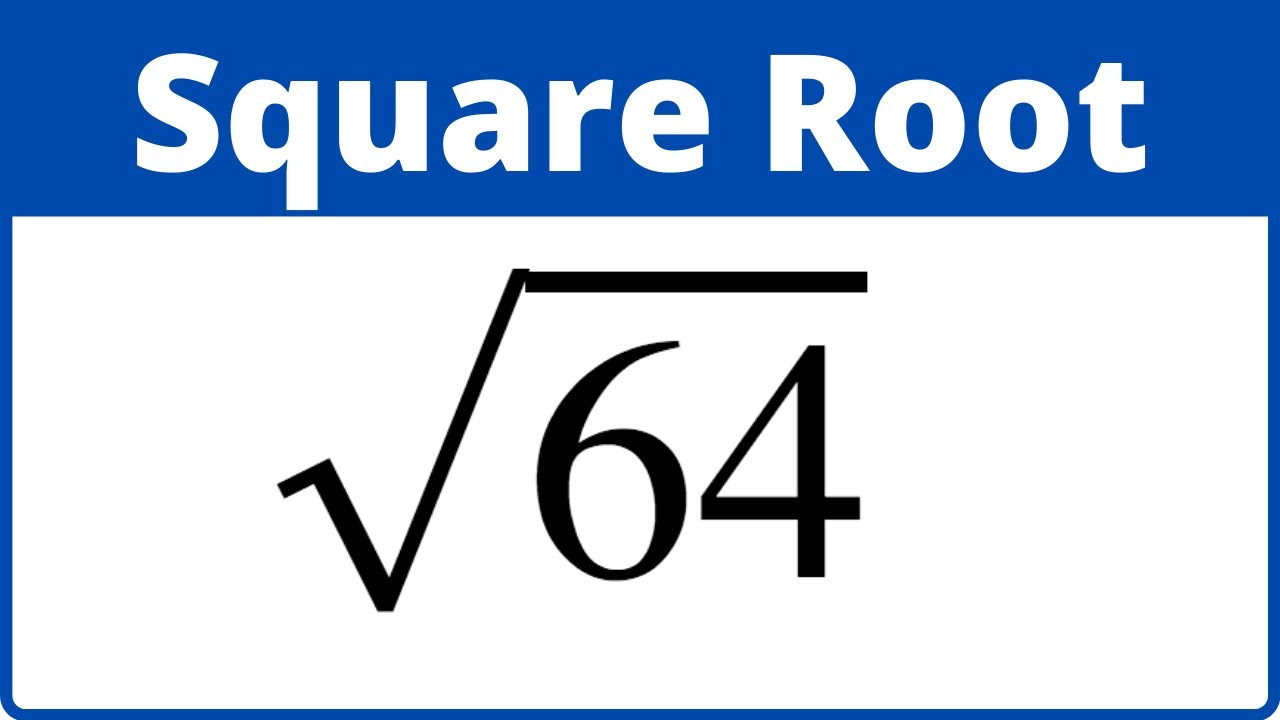
Verification of Square Roots
Verifying the square root of a number is essential to ensure the accuracy of calculations. Here are detailed steps to verify the square root of 64:
1. Squaring the Result
To verify that 8 is the square root of 64, we simply square 8:
\[
8^2 = 8 \times 8 = 64
\]
Since the result is 64, this confirms that 8 is indeed the square root of 64.
2. Using the Negative Root
Similarly, we can verify the negative square root by squaring -8:
\[
(-8)^2 = (-8) \times (-8) = 64
\]
This confirms that -8 is also a square root of 64.
3. Checking with a Calculator
Using a calculator is a quick method to verify the square root:
- Enter 64.
- Press the square root (√) button.
- The calculator should display 8.
This step confirms that 8 is the correct square root of 64.
4. Prime Factorization Method
Prime factorization involves breaking down 64 into its prime factors and verifying the square root:
\[
64 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 = 2^6
\]
To find the square root, we take half of the exponent of the prime factor:
\[
\sqrt{64} = 2^{6/2} = 2^3 = 8
\]
This confirms that 8 is the square root of 64 using prime factorization.
5. Using the Estimation Method
For a quick estimation, consider the nearest perfect squares around 64, which are 49 (7²) and 81 (9²). Since 64 is closer to 81, the square root should be closer to 8. This estimation supports that 8 is the square root of 64.
By following these steps, we can verify that the square roots of 64 are both 8 and -8.
Methods to Calculate Square Roots
Calculating the square root of a number can be achieved through various methods. Here, we explore some of the most common techniques used to find the square root of 64.
Prime Factorization Method
Prime factorization involves breaking down the number into its prime factors and then pairing the factors to find the square root.
- Start by expressing 64 as a product of prime numbers: \(64 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 = 2^6\).
- Group the prime factors into pairs: \((2 \times 2) \times (2 \times 2) \times (2 \times 2) = (2^2) \times (2^2) \times (2^2)\).
- Take one factor from each pair: \(2 \times 2 \times 2 = 8\).
- Thus, the square root of 64 is \( \sqrt{64} = 8 \).
Using a Calculator
One of the simplest ways to find the square root of a number is to use a calculator:
- Enter the number 64 into the calculator.
- Press the square root (\( \sqrt{} \)) button.
- The display will show the result, which is 8.
Estimation and Averaging Techniques
Estimation and averaging can be useful when a calculator is not available. Here's how it works:
- Find two perfect squares between which 64 lies. In this case, \( \sqrt{49} = 7 \) and \( \sqrt{81} = 9 \).
- Estimate that the square root of 64 is between 7 and 9. A good initial guess would be 8.
- Check by squaring the estimate: \( 8^2 = 64 \).
- Since the result matches 64 exactly, the estimated square root is correct, confirming \( \sqrt{64} = 8 \).
By understanding and applying these methods, one can efficiently determine the square root of any number, not just 64.
Prime Factorization
Prime factorization is a method of expressing a number as the product of its prime factors. To find the square root of a number using prime factorization, we follow these detailed steps:
- Find the Prime Factors: Break down the number into its prime factors. For 64, we divide by the smallest prime number, which is 2.
- \(64 \div 2 = 32\)
- \(32 \div 2 = 16\)
- \(16 \div 2 = 8\)
- \(8 \div 2 = 4\)
- \(4 \div 2 = 2\)
- \(2 \div 2 = 1\)
So, \(64 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 = 2^6\).
- Group the Factors into Pairs: To find the square root, we pair the prime factors:
- \((2 \times 2) \times (2 \times 2) \times (2 \times 2) = (2^2) \times (2^2) \times (2^2)\)
- Take One Factor from Each Pair: For each pair, take one factor. This is because taking the square root is essentially reversing the squaring process:
- \(2 \times 2 \times 2 = 2^3 = 8\)
Thus, the square root of 64 is \( \sqrt{64} = 8 \).
In conclusion, using prime factorization, we have shown that the square root of 64 is 8 by expressing 64 as the product of its prime factors and then simplifying.
Using a Calculator
Calculating the square root of a number using a calculator is a straightforward process. Here’s how you can do it:
-
Turn on the calculator: Ensure that your calculator is powered on and functioning properly.
-
Enter the number: Type in the number for which you want to find the square root. In this case, enter
64. -
Press the square root button: Most calculators have a button labeled with the square root symbol
√. Press this button to compute the square root. -
Read the result: The calculator will display the square root of the number. For
64, the result will be8.
Here is a step-by-step illustration of the process:
| Step | Input | Action | Result |
| 1 | Turn on the calculator | ||
| 2 | 64 | Enter the number | 64 |
| 3 | √ | Press the square root button | √64 |
| 4 | Read the result | 8 |
Using a calculator simplifies the process of finding square roots, ensuring accuracy and saving time, especially with larger numbers or more complex calculations.

Estimation and Averaging Techniques
Calculating square roots manually can be done through estimation and averaging techniques, such as the Babylonian method. This technique involves a few iterative steps to refine an initial guess until the desired accuracy is achieved. Below is a detailed explanation of how this method works:
- Initial Guess:
Start with an initial guess for the square root. For example, if you are calculating the square root of 64, you can start with 8, as it is close to the exact square root.
- First Iteration:
Divide the number (64) by your guess (8):
\[
\text{First Iteration Result} = \frac{64}{8} = 8
\] - Average the Results:
Average your guess with the result from step 2:
\[
\text{New Guess} = \frac{8 + 8}{2} = 8
\] - Repeat:
Repeat steps 2 and 3 using the new guess until the result stabilizes and the desired precision is achieved. In this case, the result is already precise after the first iteration since 8 is the exact square root of 64.
This method can be applied iteratively to other numbers, where the process might take more iterations to reach the desired level of accuracy. Here's an example using a different number for illustration:
- Example for Square Root of 50:
Initial guess: 7
- First iteration: \[ \frac{50}{7} \approx 7.14 \]
- Average: \[ \frac{7 + 7.14}{2} = 7.07 \]
- Second iteration: \[ \frac{50}{7.07} \approx 7.07 \]
- Average: \[ \frac{7.07 + 7.07}{2} = 7.07 \]
By continuously refining the guess through averaging, this method converges to a precise value for the square root.
Applications of Square Roots
Square roots play a crucial role in various real-world applications. Here are some examples:
-
Geometry and Trigonometry: Square roots are fundamental in calculating distances and dimensions in geometric shapes. For example, the Pythagorean theorem uses square roots to find the length of the hypotenuse in a right triangle:
\[ c = \sqrt{a^2 + b^2} \]
For a right triangle with sides of 6 and 8 units, the hypotenuse \( c \) is:
\[ c = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10 \]
-
Physics and Engineering: Square roots are used to determine the time it takes for an object to fall to the ground under gravity. For an object dropped from height \( h \), the time \( t \) in seconds is:
\[ t = \frac{\sqrt{h}}{4} \]
If the object is dropped from 64 feet, the time taken to reach the ground is:
\[ t = \frac{\sqrt{64}}{4} = \frac{8}{4} = 2 \text{ seconds} \]
-
Quadratic Equations: Solving quadratic equations often involves square roots. The quadratic formula, which finds the roots of \( ax^2 + bx + c = 0 \), is:
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
The discriminant \( b^2 - 4ac \) inside the square root determines the nature of the solutions.
-
Accident Investigations: In forensics, the length of skid marks can be used to estimate the speed of a vehicle before braking. The formula is:
\[ v = \sqrt{24d} \]
If skid marks are 190 feet long, the speed \( v \) is:
\[ v = \sqrt{24 \times 190} = \sqrt{4560} \approx 67.5 \text{ mph} \]
These examples illustrate how square roots are integral to solving practical problems across different fields.
In Mathematics
The square root of 64 holds significant importance in various branches of mathematics. Understanding this concept helps in grasping more complex mathematical ideas. Let's delve into how the square root of 64 is used in different mathematical contexts:
Perfect Squares
64 is a perfect square because it can be expressed as \(8^2\). In general, a perfect square is a number that can be written as the product of an integer with itself. For instance, since \(8 \times 8 = 64\), we conclude that \(\sqrt{64} = 8\).
Prime Factorization
One method to find the square root of a number is through prime factorization. For 64, we factor it into its prime components:
- 64 ÷ 2 = 32
- 32 ÷ 2 = 16
- 16 ÷ 2 = 8
- 8 ÷ 2 = 4
- 4 ÷ 2 = 2
- 2 ÷ 2 = 1
The prime factors of 64 are \(2 \times 2 \times 2 \times 2 \times 2 \times 2\) or \(2^6\). The square root is found by taking half the exponents of the prime factors, resulting in \(2^3 = 8\). Thus, \(\sqrt{64} = 8\).
Algebraic Representation
In algebra, the square root of 64 can be represented and manipulated in equations. For example, solving \(x^2 = 64\) yields two solutions: \(x = 8\) and \(x = -8\), illustrating that 64 has both a positive and negative square root.
Geometric Interpretation
Geometrically, the square root of 64 can represent the side length of a square with an area of 64 square units. If a square has an area of 64, each side must be \(\sqrt{64} = 8\) units long.
Applications in Higher Mathematics
The concept of square roots is foundational in calculus and advanced algebra. For example, solving quadratic equations, analyzing functions, and computing integrals often require understanding square roots. The function \(f(x) = \sqrt{x}\) is fundamental in various mathematical analyses and problem-solving techniques.
Rational and Irrational Numbers
The square root of 64 is a rational number because it can be expressed as the fraction \(\frac{8}{1}\). In contrast, many other square roots (like \(\sqrt{2}\)) are irrational, meaning they cannot be written as a simple fraction and have non-repeating, non-terminating decimal expansions.
Understanding the square root of 64 is not just about finding a number that, when multiplied by itself, gives 64. It connects various mathematical principles, from basic arithmetic to advanced theoretical concepts, demonstrating the elegance and interconnectedness of mathematics.
In Real Life
The square root of 64, which is 8, finds numerous applications in various real-life scenarios. Understanding square roots can enhance problem-solving skills and practical knowledge in different fields. Here are some examples:
- Architecture and Construction: Architects and builders often use square roots when designing and constructing buildings. For example, to create a square room with an area of 64 square feet, the side length of the room would be the square root of 64, which is 8 feet.
- Carpentry: Carpenters use square roots to determine the lengths of sides in right-angled triangles, an application of the Pythagorean theorem. For instance, if a square piece of wood has an area of 64 square inches, each side will measure 8 inches.
- Physics: In physics, square roots are used in formulas to calculate various properties. For instance, the period of a simple pendulum (T) is proportional to the square root of its length (L), expressed as \( T = 2\pi \sqrt{\frac{L}{g}} \), where \( g \) is the acceleration due to gravity.
- Finance: In finance, the square root is used in calculating the standard deviation and variance, which measure the volatility of stock prices. For example, if the variance of a stock's return is 64, the standard deviation is the square root of 64, which is 8, indicating the degree of variation in the stock's returns.
- Technology: In computer graphics, square roots are essential for calculating distances and dimensions in pixel spaces. For example, the diagonal resolution of a square screen with an area of 64 square inches can be found by taking the square root of 64.
- Sports: In sports like track and field, the concept of square roots can be used to design and measure the dimensions of fields and tracks. For example, ensuring that an 8x8 meter square area is prepared for a specific event.
These are just a few examples demonstrating how the square root of 64 and square roots, in general, play a crucial role in various practical applications. Understanding this mathematical concept can provide significant benefits in both professional and everyday contexts.

Common Questions About Square Roots
Understanding square roots can often raise several common questions. Below, we address some of the most frequently asked questions regarding square roots.
- What is a square root?
A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 64 is 8 because \(8 \times 8 = 64\).
- What are the square roots of 64?
The square roots of 64 are 8 and -8, because both \(8^2\) and \((-8)^2\) equal 64. The positive root is often referred to as the principal square root.
- Is the square root of 64 a rational number?
Yes, the square root of 64 is rational. A rational number can be expressed as the quotient of two integers. Since 8 is an integer, it is also rational.
- How can you find the square root of 64?
There are several methods to find the square root of 64:
- Using a calculator: Simply enter 64 and press the square root button to get 8.
- Prime factorization: Since \(64 = 2^6\), you can pair the factors to get \(\sqrt{64} = \sqrt{(2^3)^2} = 2^3 = 8\).
- Estimation: By identifying that 64 is a perfect square, you can directly know that the square root is 8.
- Why do square roots have two values?
Square roots have two values, a positive and a negative, because both \( (positive \ value)^2 \) and \( (negative \ value)^2 \) result in the same positive number. For example, both \(8^2\) and \((-8)^2\) equal 64.
- What are the applications of square roots in real life?
Square roots are used in various real-life applications such as in geometry to find the side lengths of squares and in physics to solve equations involving area and energy.
- What is the difference between a perfect square and a non-perfect square?
A perfect square is a number that has an integer as its square root. For example, 64 is a perfect square because its square root is 8, an integer. A non-perfect square has a square root that is not an integer, resulting in an irrational number.
Căn Bậc Hai của 64: Hướng Dẫn Chi Tiết
READ MORE:
Cách Tính Căn Bậc Hai của 64: Sqrt(64)