Topic what is square root of 61: The square root of 61 is a fascinating number with significant applications in various fields such as mathematics, physics, and engineering. In this article, we explore the precise value, methods of calculation, and the importance of understanding the square root of 61 in practical and theoretical contexts.
Table of Content
- Square Root of 61
- Introduction
- Definition of Square Root
- Mathematical Representation of Square Root of 61
- Decimal Approximation of Square Root of 61
- Properties of Square Root of 61
- Methods to Calculate Square Root of 61
- Long Division Method
- Calculator Method
- Applications of Square Root of 61
- Square Root of 61 in Geometry
- Square Root of 61 in Algebra
- Importance in Physics and Engineering
- Continued Fraction Representation
- Prime Factorization
- Common Misconceptions
- YOUTUBE: Khám phá căn bậc hai của 61 với video này. Học cách tính toán và ứng dụng trong toán học, vật lý và kỹ thuật.
Square Root of 61
The square root of 61 is an irrational number, which means it cannot be exactly expressed as a simple fraction. Instead, it is often represented in its decimal form or as a continued fraction. The square root of 61 can be approximated and calculated using various methods.
Decimal Form
The square root of 61 in decimal form is approximately:
\(\sqrt{61} \approx 7.810249675906654\)
Radical Form
In its simplest radical form, the square root of 61 is represented as:
\(\sqrt{61}\)
Continued Fraction
The continued fraction representation of the square root of 61 is a more complex form of expressing the number, which is useful in some advanced mathematical contexts. It can be written as:
\(\sqrt{61} = [7; \overline{1, 4, 3, 1, 2, 2, 1, 3, 4, 1, 14}]\)
Methods of Calculation
There are several methods to calculate the square root of 61:
- Prime Factorization: This method is not practical here as 61 is a prime number.
- Long Division Method: A manual method to find a more precise value of the square root.
- Using a Calculator: The most common and easiest way to find the square root.
Applications
Knowing the square root of 61 is useful in various fields such as engineering, physics, and mathematics, where precise calculations are necessary. It is often used in solving quadratic equations, analyzing geometric shapes, and other mathematical problems.
Conclusion
Although the exact value of the square root of 61 is an irrational number, its approximate value is widely used in practical applications. Understanding different methods of calculating and representing the square root helps in various mathematical and scientific computations.
READ MORE:
Introduction
The square root of 61, denoted as \(\sqrt{61}\), is a number that, when multiplied by itself, equals 61. This mathematical concept is fundamental in various areas, including algebra, geometry, and real-world applications. Unlike perfect squares, 61 is a prime number, making its square root an irrational number that cannot be expressed as a simple fraction.
To understand the square root of 61 better, we will cover several key aspects:
- Mathematical representation and properties of \(\sqrt{61}\)
- Approximate decimal value and its significance
- Methods to calculate the square root of 61
- Applications in different fields
- Common misconceptions and clarifications
By exploring these topics, we aim to provide a comprehensive understanding of the square root of 61, highlighting its importance and utility in both theoretical and practical contexts.
Definition of Square Root
The square root of a number is a value that, when multiplied by itself, yields the original number. It is one of the fundamental operations in mathematics, essential for solving equations and understanding various concepts in algebra and geometry.
Mathematically, the square root of a number \( x \) is denoted as \(\sqrt{x}\). For instance:
- The square root of 4 is 2 because \(2 \times 2 = 4\).
- The square root of 9 is 3 because \(3 \times 3 = 9\).
- The square root of 61 is \(\sqrt{61}\), which is approximately 7.81 because \(7.81 \times 7.81 \approx 61\).
Square roots can be either positive or negative because both \((\sqrt{x})^2\) and \((-\sqrt{x})^2\) equal \( x \). For example, both 2 and -2 are square roots of 4. However, the principal square root is usually taken to be the positive value.
There are various methods to find the square root of a number, including:
- Prime Factorization: Breaking down the number into its prime factors and pairing them to find the square root.
- Long Division Method: A manual process to find the square root to a desired level of accuracy.
- Using a Calculator: The most straightforward method to obtain an approximate value of the square root quickly.
In the case of non-perfect squares like 61, the square root is an irrational number, meaning it cannot be expressed as a simple fraction and has a non-repeating, non-terminating decimal expansion.
Mathematical Representation of Square Root of 61
The square root of 61, denoted as \(\sqrt{61}\), is an irrational number, meaning it cannot be exactly expressed as a simple fraction and its decimal representation is non-terminating and non-repeating. Here is a detailed look at the mathematical representation of \(\sqrt{61}\):
Radical Form: The simplest way to represent the square root of 61 is using the radical symbol:
\(\sqrt{61}\)
Decimal Approximation: While \(\sqrt{61}\) cannot be expressed exactly as a decimal, it can be approximated to several decimal places:
\(\sqrt{61} \approx 7.810249675906654\)
Continued Fraction Representation: For a more precise and structured representation, \(\sqrt{61}\) can be expressed as a continued fraction. This is particularly useful in advanced mathematical contexts:
\(\sqrt{61} = [7; \overline{1, 4, 3, 1, 2, 2, 1, 3, 4, 1, 14}]\)
Prime Factorization: Although prime factorization is more useful for perfect squares, it is worth noting that 61 is a prime number. Thus, it cannot be simplified further using prime factors, reinforcing the fact that \(\sqrt{61}\) is irrational.
Below is a table summarizing the key representations of the square root of 61:
| Representation | Form |
|---|---|
| Radical | \(\sqrt{61}\) |
| Decimal | 7.810249675906654 |
| Continued Fraction | [7; \overline{1, 4, 3, 1, 2, 2, 1, 3, 4, 1, 14}] |
Understanding these different representations helps in various mathematical calculations and theoretical applications, providing a comprehensive view of the nature of \(\sqrt{61}\).
Decimal Approximation of Square Root of 61
The square root of 61 is an irrational number, meaning it cannot be precisely represented as a fraction or a finite decimal. However, it can be approximated to a high degree of accuracy using decimal notation. Here, we explore the steps to approximate the square root of 61:
Using a Calculator:
The most straightforward method to find the decimal approximation of \(\sqrt{61}\) is by using a calculator. Most scientific calculators provide the square root function, yielding an approximate value quickly:
\(\sqrt{61} \approx 7.810249675906654\)
Long Division Method:
For a manual approach, the long division method can be used to approximate the square root to several decimal places. Here is a step-by-step outline:
- Estimate an initial guess. For \(\sqrt{61}\), a reasonable guess might be 7.8 since \(7.8 \times 7.8 = 60.84\).
- Divide 61 by the guess (7.8), giving approximately 7.821.
- Averaging the guess and the result gives a new approximation: \((7.8 + 7.821) / 2 \approx 7.8105\).
- Repeat the process to refine the approximation. With each iteration, the value converges to a more accurate result.
Decimal Expansion:
The decimal expansion of \(\sqrt{61}\) is non-terminating and non-repeating, which are characteristics of irrational numbers. To illustrate:
\(\sqrt{61} \approx 7.810249675906654...\)
Table of Approximations:
The following table shows the square root of 61 approximated to various decimal places:
| Decimal Places | Approximation |
|---|---|
| 1 | 7.8 |
| 2 | 7.81 |
| 4 | 7.8102 |
| 8 | 7.81024968 |
| 16 | 7.810249675906654 |
Understanding the decimal approximation of \(\sqrt{61}\) is crucial for practical calculations and helps in recognizing the irrational nature of the number.

Properties of Square Root of 61
The square root of 61, represented as \(\sqrt{61}\), possesses several unique properties that are important in mathematical contexts. Below, we explore these properties in detail:
- Irrational Number: The square root of 61 is an irrational number, which means it cannot be expressed as a simple fraction. Its decimal form is non-terminating and non-repeating:
- Positive and Negative Roots: Every positive real number has two square roots: one positive and one negative. For 61, these are:
- Prime Number Property: Since 61 is a prime number, its square root cannot be simplified using prime factorization. This reinforces its status as an irrational number.
- Algebraic Properties: The square root of 61 adheres to the general properties of square roots in algebra:
- \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\)
- \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
- \((\sqrt{a})^2 = a\)
- Continued Fraction Representation: The continued fraction for \(\sqrt{61}\) is periodic after the initial term, reflecting its irrationality:
- Geometric Interpretation: Geometrically, the square root of 61 represents the length of the hypotenuse of a right triangle with legs of certain lengths. For instance, a right triangle with legs of approximately 7.8 units each would have a hypotenuse close to \(\sqrt{61}\).
- Approximation and Computation: The square root of 61 can be approximated using methods such as the long division method or by using a calculator for more precise results. It is essential in various calculations in science, engineering, and mathematics.
\(\sqrt{61} \approx 7.810249675906654\)
\(\sqrt{61}\) and \(-\sqrt{61}\)
\(\sqrt{61} = [7; \overline{1, 4, 3, 1, 2, 2, 1, 3, 4, 1, 14}]\)
These properties make the square root of 61 a significant number in various theoretical and practical applications, highlighting its importance in different fields of study.
Methods to Calculate Square Root of 61
Calculating the square root of 61 involves several methods, each varying in complexity and accuracy. Below are the detailed methods to find \(\sqrt{61}\):
- Using a Calculator:
The simplest and quickest way to find the square root of 61 is to use a scientific calculator. Most calculators have a square root function that will give you an approximate value instantly:
\(\sqrt{61} \approx 7.810249675906654\)
- Long Division Method:
This manual method allows you to find the square root to a desired level of accuracy by following these steps:
- Group the digits of the number in pairs, starting from the decimal point and moving both left and right. For 61, we consider it as 61.0000...
- Find the largest number whose square is less than or equal to the first group. Here, 7 because \(7^2 = 49\).
- Subtract \(49\) from \(61\), giving \(12\), and bring down the next pair of zeros to get \(1200\).
- Double the current quotient (7) to get 14 and determine the next digit (x) such that \(14x \cdot x \leq 1200\). Here, \(8\) works because \(148 \cdot 8 = 1184\).
- Subtract \(1184\) from \(1200\) to get \(16\), bring down the next pair of zeros to get \(1600\), and repeat the process to refine the approximation.
Continuing this process yields the decimal expansion of \(\sqrt{61}\).
- Approximation Methods:
- Babylonian (Heron’s) Method:
An iterative method to approximate square roots. Start with an initial guess (e.g., 7.8) and iterate using:
\(x_{n+1} = \frac{1}{2} \left( x_n + \frac{61}{x_n} \right)\)
After several iterations, this method converges to a value close to \(7.810249675906654\).
- Newton’s Method:
Similar to the Babylonian method, Newton's method uses the formula:
\(x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}\)
For \(f(x) = x^2 - 61\), the iteration becomes:
\(x_{n+1} = \frac{1}{2} \left( x_n + \frac{61}{x_n} \right)\)
- Babylonian (Heron’s) Method:
- Using Estimation:
For rough estimates, find two perfect squares between which 61 lies (49 and 64):
- \(7^2 = 49\)
- \(8^2 = 64\)
Since \(61\) is closer to \(64\), \(\sqrt{61}\) is slightly less than \(8\). Refining this estimate through interpolation can yield more accurate results.
These methods, ranging from simple to complex, provide a variety of approaches to finding the square root of 61, each useful in different scenarios depending on the required accuracy and available tools.
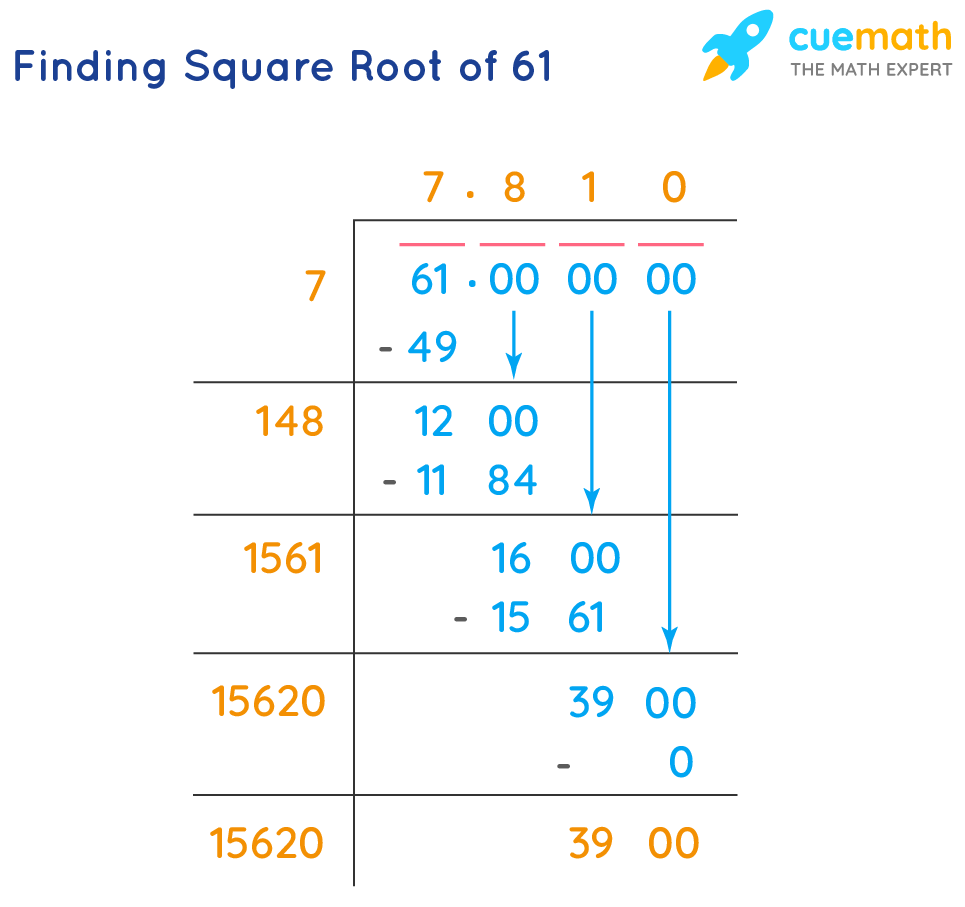
Long Division Method
The long division method is a manual technique to find the square root of a number. Here is a detailed, step-by-step explanation of how to use the long division method to calculate the square root of 61:
- Pair the Digits: Start by pairing the digits of the number from right to left. For 61, we have a single pair: 61.
- Find the Largest Square: Find the largest square number less than or equal to 61. The largest square is 49 (72), so the first digit of the square root is 7.
- Subtract and Bring Down:
- Subtract 49 from 61, giving 12.
- Bring down two zeros to the right of 12, making it 1200.
- Double the Quotient: Double the current quotient (7) and write it as 14. This will be the starting part of the new divisor.
- Find the Next Digit:
- Find a digit (x) such that 14x * x is less than or equal to 1200.
- Test different values for x. For x = 8, 148 * 8 = 1184, which is less than 1200.
- So, the next digit of the square root is 8.
- Subtract and Continue:
- Subtract 1184 from 1200, giving 16.
- Bring down two more zeros, making it 1600.
- Double the current quotient (78) to get 156. Find the next digit (y) such that 156y * y is less than or equal to 1600.
- Continue this process to get a more accurate value of the square root.
Following this method, you can approximate the square root of 61 step by step. This manual process helps in understanding the underlying mathematics and provides a way to find square roots without a calculator.
Calculator Method
The calculator method is the simplest way to find the square root of 61. Here's how you can do it using a basic calculator or a software tool like Excel or Google Sheets.
Using a Basic Calculator
- Turn on your calculator.
- Enter the number 61.
- Press the square root button (√). This button might be labeled differently depending on your calculator model, but it generally looks like √ or may require you to press a "shift" or "2nd" key first.
- Read the result, which should be approximately 7.8102.
Using Excel or Google Sheets
To calculate the square root of 61 using Excel or Google Sheets, follow these steps:
- Open a new spreadsheet in Excel or Google Sheets.
- Click on an empty cell where you want the result to be displayed.
- Type the formula:
=SQRT(61) - Press Enter. The cell will display the square root of 61, which is approximately 7.8102.
This method is efficient and allows for quick calculations of square roots for any number, not just 61.
Applications of Square Root of 61
The square root of 61, approximately 7.81, has various applications across multiple fields. Below are some practical examples where the square root of 61 is useful:
- Geometry: In geometry, the square root of 61 can be used to calculate the diagonal length of a square or rectangle when the area is known. For instance, if the area of a square is 61 square units, the length of each side would be √61 units, providing critical measurements for construction and design.
- Physics: The square root of 61 can be utilized in formulas involving gravitational force and acceleration. For example, in determining the time it takes for an object to fall from a certain height, the square root function often appears in the equations used for these calculations.
- Engineering: In electrical engineering, the square root of 61 might be used to calculate parameters such as impedance in AC circuits, where the calculation involves the square root of the sum of the squares of resistance and reactance. Similarly, it's applicable in calculating stress and strain in materials.
- Statistics: In statistical analysis, the square root is crucial for computing standard deviations and variances. If a data set has a variance of 61, the standard deviation would be √61, helping in understanding data spread and distribution.
- Computer Science: In computer algorithms, especially those involving cryptography, the square root of prime numbers like 61 is often used in encryption algorithms to secure data transmission. This application is vital in maintaining the integrity and confidentiality of information in digital communications.
- Architecture: Architects and designers use square roots in their calculations to ensure precise measurements. For instance, if designing a garden or a room that requires a particular area, using the square root helps in determining the necessary dimensions for space planning.
These applications demonstrate how the square root of 61 is not only a mathematical concept but also a practical tool in various scientific, engineering, and technological domains.
Square Root of 61 in Geometry
The square root of 61, approximately 7.810, finds its applications in various geometric contexts. Here are some of the ways it can be utilized:
-
Diagonal of a Rectangle: In geometry, the square root of 61 can be used to determine the diagonal of a rectangle. For example, if a rectangle has sides of lengths 5 and 6 units, the diagonal \(d\) can be found using the Pythagorean theorem:
\[
d = \sqrt{5^2 + 6^2} = \sqrt{25 + 36} = \sqrt{61} \approx 7.810
\] -
Distance Between Points: The square root of 61 is also useful in finding the distance between two points in a coordinate plane. Given points \(A(x_1, y_1)\) and \(B(x_2, y_2)\), the distance \(d\) between them is:
\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]If \((x_2 - x_1)^2 + (y_2 - y_1)^2\) equals 61, then \(d = \sqrt{61} \approx 7.810\).
-
Area of an Equilateral Triangle: The square root of 61 can appear in the calculation of areas of triangles, especially when dealing with complex coordinate points or in advanced problems involving Heron's formula. For an equilateral triangle with side length \(s\), the height \(h\) is given by:
\[
h = \frac{\sqrt{3}}{2} s
\]If the side length is adjusted such that the height calculation involves the square root of 61, this concept can be extended to various geometric constructions.
-
Radius of a Circle: In problems involving circles, the square root of 61 can be used to find the radius when dealing with specific area calculations. If the area \(A\) of a circle is given by \(A = \pi r^2\) and solving for \(r\) leads to an equation involving the square root of 61, then:
\[
r = \sqrt{\frac{A}{\pi}} = \sqrt{61} \approx 7.810
\]
These examples illustrate how the square root of 61 integrates into geometric calculations, enhancing understanding and solving complex problems.
Square Root of 61 in Algebra
In algebra, the square root of 61 has several important applications and properties that are essential for understanding various algebraic concepts. Here, we will explore how the square root of 61 is represented and used in algebraic expressions and equations.
Representation:
- In radical form: √61
- In exponential form: \(61^{1/2}\)
- In decimal form: Approximately 7.81024967591
Properties:
- The square root of 61 is an irrational number because it cannot be expressed as a ratio of two integers. Its decimal representation is non-terminating and non-repeating.
- The square root function is one of the most fundamental operations in algebra, and the square root of 61 is often used in solving quadratic equations where the solutions are not perfect squares.
Example in an Equation:
Consider the quadratic equation:
\(x^2 - 61 = 0\)
To solve for \(x\), we can take the square root of both sides:
\(x = \pm\sqrt{61}\)
Thus, the solutions are \(x = \pm 7.81024967591\).
Application in Solving Systems of Equations:
Suppose we have a system of equations where one of the equations involves the square root of 61. For instance:
\(2x + \sqrt{61} = 10\)
To isolate \(x\), we first subtract \(\sqrt{61}\) from both sides:
\(2x = 10 - \sqrt{61}\)
Then, divide by 2:
\(x = \frac{10 - \sqrt{61}}{2}\)
Application in Algebraic Functions:
The square root of 61 can also be seen in algebraic functions. For example, in the function:
\(f(x) = \sqrt{61 - x^2}\)
This function defines a semi-circle with radius \(\sqrt{61}\), highlighting its geometric interpretation as well.
By understanding the properties and applications of the square root of 61 in algebra, students can gain a deeper insight into solving complex algebraic problems and understanding the behavior of irrational numbers in mathematical equations.
Importance in Physics and Engineering
The square root of 61 has significant applications in various fields of physics and engineering. Below, we explore its importance in different contexts:
1. Electrical Engineering
In electrical engineering, the concept of Root Mean Square (RMS) is crucial. RMS is used to determine the effective value of an alternating current (AC) signal, which is essential for designing and analyzing electrical circuits. The RMS value of a waveform, like a sine wave, is found by taking the square root of the mean of the squares of the instantaneous values over one cycle. This effective value is necessary for calculating power dissipation in resistors, ensuring that components are designed to handle the appropriate levels of current and voltage.
For example, to find the RMS value of a sine wave with a peak voltage \(V_{peak}\), the formula is:
\[ V_{RMS} = \frac{V_{peak}}{\sqrt{2}} \]
2. Structural Engineering
In structural engineering, square roots are often used to calculate the natural frequencies of structures such as bridges and buildings. These frequencies help engineers predict how a structure will respond to various loads, including wind, traffic, and seismic activity. Understanding these responses is crucial for ensuring structural integrity and safety.
For instance, the natural frequency \(f_n\) of a simple structure can be approximated using the formula:
\[ f_n = \frac{1}{2\pi} \sqrt{\frac{k}{m}} \]
where \(k\) is the stiffness of the structure and \(m\) is the mass.
3. Physics - Wave Mechanics
In physics, particularly in wave mechanics, the square root function is used to describe the relationship between different properties of waves. For example, the velocity \(v\) of a wave on a string is related to the tension \(T\) and linear mass density \(\mu\) by the equation:
\[ v = \sqrt{\frac{T}{\mu}} \]
This relationship is essential for understanding how waves propagate in different media and is applied in various technologies, from musical instruments to communication systems.
4. Quantum Mechanics
Square roots appear frequently in quantum mechanics, particularly in the normalization of wave functions. The probability density of finding a particle in a particular state is given by the square of the wave function's magnitude. Normalizing the wave function ensures that the total probability across all space is equal to one, which involves calculating the square root of the integral of the squared wave function.
For a normalized wave function \(\psi(x)\), the condition is:
\[ \int_{-\infty}^{\infty} |\psi(x)|^2 \, dx = 1 \]
5. Signal Processing
In signal processing, the square root function is used to compute the magnitude of a complex number, which represents the amplitude of a signal. This is particularly important in the analysis and filtering of signals in various applications, including audio engineering, telecommunications, and medical imaging.
The magnitude \( |z| \) of a complex number \( z = a + bi \) is given by:
\[ |z| = \sqrt{a^2 + b^2} \]
These examples illustrate how the square root function, including specific values like the square root of 61, plays a critical role in various fields of physics and engineering, contributing to our understanding and development of numerous technologies.

Continued Fraction Representation
The continued fraction representation of the square root of 61 is a way to express this irrational number as a sequence of integer terms. This representation is particularly useful in various mathematical and computational applications because it allows for a precise approximation of the number.
The continued fraction for the square root of 61 can be written as:
\[ \sqrt{61} = 7 + \cfrac{1}{1 + \cfrac{1}{3 + \cfrac{1}{1 + \cfrac{1}{2 + \cfrac{1}{7 + \cfrac{1}{1 + \cfrac{1}{3 + \cfrac{1}{1 + \cfrac{1}{2 + \ddots}}}}}}}}}} \]
This fraction can also be represented in a more compact form as:
\[ \sqrt{61} = [7; \overline{1, 3, 1, 2, 7, 1, 3, 1, 2}] \]
The sequence \(\overline{1, 3, 1, 2, 7, 1, 3, 1, 2}\) repeats indefinitely. Here's a breakdown of the terms:
- The initial term, 7, is the integer part of \(\sqrt{61}\).
- The periodic part of the sequence is {1, 3, 1, 2, 7, 1, 3, 1, 2}, which continues infinitely.
The continued fraction representation has several interesting properties:
- Periodic Sequence: After the initial term, the sequence of denominators in the continued fraction for \(\sqrt{61}\) becomes periodic.
- Convergence: The continued fraction representation converges to the true value of \(\sqrt{61}\) more quickly than the simple decimal approximation.
- Applications: This representation is used in solving Diophantine equations, number theory, and for precise numerical computations in algorithms.
Continued fractions provide a deeper understanding of the properties of square roots and their behavior as irrational numbers. They offer a way to achieve precise approximations and are instrumental in various advanced mathematical applications.
Prime Factorization
The prime factorization of a number involves breaking it down into its prime number factors. Prime numbers are those greater than 1 that have no divisors other than 1 and themselves.
For the number 61, the prime factorization process is straightforward because 61 is a prime number. This means it cannot be divided evenly by any number other than 1 and itself. Here is how the prime factorization of 61 is determined:
- 61 is checked for divisibility by prime numbers starting from the smallest prime (2). Since 61 is odd, it is not divisible by 2.
- Next, 61 is checked for divisibility by 3. The sum of the digits of 61 (6 + 1 = 7) is not divisible by 3, so 61 is not divisible by 3.
- 61 is also not divisible by the next few primes (5, 7, etc.) as it does not end in 0 or 5, and it does not produce an integer quotient when divided by 7.
- Finally, 61 is tested against itself. Since 61 divided by 61 equals 1, it confirms that 61 is only divisible by 1 and 61.
Thus, the prime factorization of 61 can be written as:
In exponential form, it is represented as:
The factor tree for 61 demonstrates its prime factorization as follows:
| 61 | /\ | 61 | 1 |
Therefore, the prime factor of 61 is simply 61 itself, highlighting its status as a prime number.
Common Misconceptions
Understanding the square root of a number can sometimes lead to common misconceptions. Here are some typical misunderstandings related to the square root of 61:
- Misinterpreting the Square Root Symbol: One common error is thinking that the square root of a sum is the sum of the square roots, i.e., \(\sqrt{a + b} = \sqrt{a} + \sqrt{b}\). For example, \(\sqrt{61 + 1} \neq \sqrt{61} + \sqrt{1}\).
- Incorrect Simplification: Some might incorrectly simplify square roots by misapplying properties of roots. For instance, assuming \(\sqrt{61} \cdot \sqrt{1} = \sqrt{61 \cdot 1}\) holds true, but it's essential to handle each root separately.
- Precision and Approximations: The square root of 61 is an irrational number, often approximated as 7.81. Misunderstanding this can lead to errors in calculations requiring high precision.
- Mixing Exponents and Roots: Another frequent misconception is confusing the operations involving exponents and roots, such as \((\sqrt{61})^2 = 61\), but \((\sqrt{61} + 1)^2 \neq 61 + 1\).
- Arithmetic Operations: Misunderstanding how to combine square roots in arithmetic operations can lead to errors. For example, thinking that \(3\sqrt{61} + 2\sqrt{61} = 5\sqrt{61}\) is correct, while the proper approach is adding the coefficients, not altering the radicand.
To avoid these misconceptions, it's crucial to understand the properties of square roots and apply them correctly in various mathematical contexts. Practice and clear conceptual understanding are key to mastering the correct usage of square roots.
Khám phá căn bậc hai của 61 với video này. Học cách tính toán và ứng dụng trong toán học, vật lý và kỹ thuật.
Căn bậc hai của 61
READ MORE:
Khám phá cách tính căn bậc hai của 61 và các ứng dụng thực tiễn của nó trong toán học và kỹ thuật.
Căn Bậc Hai của 61