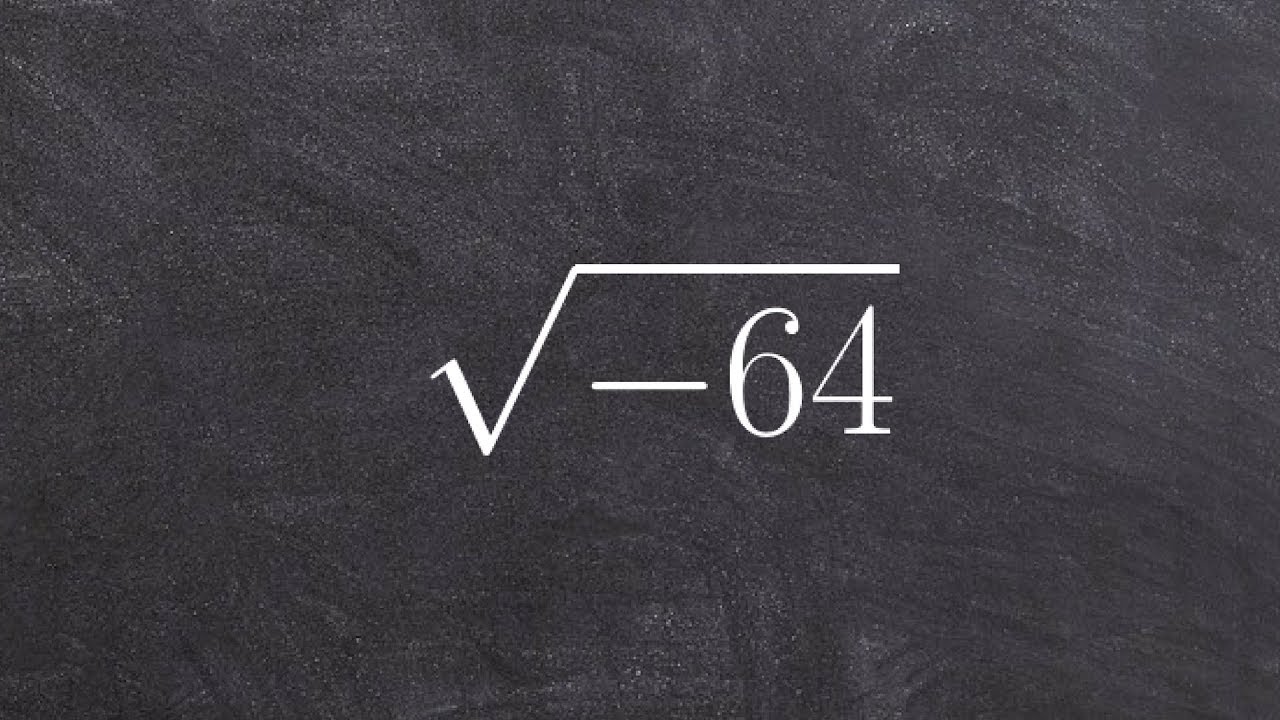Topic what is square root of 60: Curious about the square root of 60? This article provides a comprehensive look at \( \sqrt{60} \), its decimal form, simplified radical expression, and practical applications in various fields. Whether for academic purposes or general knowledge, uncover the fascinating details of the square root of 60 here.
Table of Content
- Square Root of 60
- Introduction to Square Roots
- Understanding the Square Root of 60
- Decimal Representation of Square Root of 60
- Simplified Radical Form of Square Root of 60
- Methods to Calculate Square Root of 60
- Long Division Method
- Newton's Method
- Using a Calculator
- Applications of Square Root of 60
- Geometry Applications
- Physics Applications
- Engineering Applications
- Estimating the Square Root of 60
- Comparing Square Roots of Nearby Numbers
- Prime Factorization Method
- Practical Examples Involving Square Root of 60
- Common Misconceptions About Square Roots
- Visualizing the Square Root of 60
- YOUTUBE: Video hướng dẫn đơn giản hóa căn bậc hai của 60, giúp bạn hiểu rõ hơn về khái niệm này.
Square Root of 60
The square root of 60, denoted as \( \sqrt{60} \), is a value that, when multiplied by itself, gives the number 60. The square root of 60 is not a perfect square, meaning it does not yield an integer.
Decimal Form
The decimal form of \( \sqrt{60} \) is approximately:
\[
\sqrt{60} \approx 7.745966692414834
\]
Simplified Radical Form
The square root of 60 can be simplified by factoring 60 into its prime factors:
\[
60 = 2^2 \times 3 \times 5
\]
This allows us to simplify the square root:
\[
\sqrt{60} = \sqrt{2^2 \times 3 \times 5} = \sqrt{2^2} \times \sqrt{3} \times \sqrt{5} = 2 \sqrt{15}
\]
Approximation and Estimation
For practical purposes, the square root of 60 can be estimated. It lies between the square roots of 49 and 64, which are 7 and 8 respectively:
- \( \sqrt{49} = 7 \)
- \( \sqrt{64} = 8 \)
Thus, \( \sqrt{60} \) is approximately 7.75.
Calculation Methods
There are several methods to calculate the square root of 60:
- Long Division Method: This manual method involves a step-by-step approach to find the decimal expansion.
- Newton's Method: An iterative method that starts with an initial guess and improves the approximation through iterations.
- Using a Calculator: The quickest way to find the square root of 60 to a high degree of accuracy.
Applications
The square root of 60 has applications in various fields such as:
- Geometry: In finding the length of the diagonal of a rectangle with side lengths involving the square root of 60.
- Physics: In calculations involving areas and distances where 60 is a relevant factor.
- Engineering: In designing systems and components where precise measurements are required.
READ MORE:
Introduction to Square Roots
Square roots are fundamental mathematical concepts that represent one of the two equal factors of a number. The square root of a number \( x \) is a value \( y \) such that \( y^2 = x \). For example, the square root of 25 is 5 because \( 5^2 = 25 \).
Here are some key points to understand square roots:
- Square roots can be both positive and negative, but the principal square root is always the non-negative value.
- Perfect squares are numbers that have integer square roots. Examples include 1, 4, 9, 16, 25, and so on.
- Non-perfect squares have square roots that are irrational numbers, which cannot be expressed as a simple fraction.
The notation for the square root of a number is \( \sqrt{x} \). For instance, \( \sqrt{36} = 6 \) because \( 6^2 = 36 \).
Calculating square roots can be done using various methods:
- Prime Factorization: Breaking down the number into its prime factors and simplifying.
- Long Division Method: A manual method to find the square root step by step.
- Using a Calculator: The most straightforward method for quick and accurate results.
- Approximation: Estimating the square root by finding two close perfect squares.
Understanding square roots is essential in various fields such as mathematics, physics, engineering, and many real-life applications where measurements and calculations are involved.
Understanding the Square Root of 60
The square root of 60, denoted as \( \sqrt{60} \), is the value that, when multiplied by itself, equals 60. This value is not an integer, making 60 a non-perfect square.
To better understand \( \sqrt{60} \), let's explore its different forms:
Decimal Representation
The square root of 60 in decimal form is approximately:
\[
\sqrt{60} \approx 7.745966692414834
\]
Simplified Radical Form
We can simplify \( \sqrt{60} \) by breaking down 60 into its prime factors:
\[
60 = 2^2 \times 3 \times 5
\]
This allows us to express the square root in a simplified radical form:
\[
\sqrt{60} = \sqrt{2^2 \times 3 \times 5} = \sqrt{2^2} \times \sqrt{3} \times \sqrt{5} = 2 \sqrt{15}
\]
Calculation Methods
There are several methods to calculate the square root of 60:
- Prime Factorization: As demonstrated above, this involves simplifying the radical by breaking down the number into its prime factors.
- Long Division Method: This manual method finds the square root step-by-step, providing a detailed approximation.
- Using a Calculator: The quickest and most accurate way to find \( \sqrt{60} \). Most scientific calculators have a square root function.
- Newton's Method: An iterative numerical method to approximate the square root by starting with an initial guess and refining it through iterations.
Practical Applications
The square root of 60 is used in various practical applications:
- Geometry: Calculating the diagonal of a rectangle or the side length of a square with an area of 60 square units.
- Physics: Solving problems involving areas and distances where the number 60 appears.
- Engineering: Design and analysis in scenarios where precise measurements are necessary.
Understanding the square root of 60 provides insight into both its theoretical and practical aspects, enhancing our comprehension of mathematical concepts and their real-world applications.
Decimal Representation of Square Root of 60
The square root of 60, when expressed as a decimal, provides an approximate value that is useful for various calculations and practical applications. The decimal representation is a non-repeating, non-terminating number, characteristic of an irrational number.
To find the decimal representation of \( \sqrt{60} \), we can use a calculator or a numerical method. The result is approximately:
\[
\sqrt{60} \approx 7.745966692414834
\]
This value is accurate to many decimal places, but for most practical purposes, it can be rounded to a few decimal places. Common approximations include:
- To 2 decimal places: \( \sqrt{60} \approx 7.75 \)
- To 3 decimal places: \( \sqrt{60} \approx 7.746 \)
- To 4 decimal places: \( \sqrt{60} \approx 7.7459 \)
These rounded values make it easier to use the square root of 60 in real-world applications without needing the full precision of the exact decimal value.
Step-by-Step Approximation
To understand how we arrive at the decimal representation, we can use the long division method to approximate \( \sqrt{60} \) step-by-step:
- Estimate an initial value: Start with a close estimate. Since \( 7^2 = 49 \) and \( 8^2 = 64 \), we know \( \sqrt{60} \) is between 7 and 8.
- Refine the estimate: Use the average method or another iterative method to get closer. For example, averaging 7.7 and 7.8, then squaring to see which is closer to 60.
- Continue refining: Repeat the process to get a more accurate value, resulting in 7.745966692414834.
Using these steps, one can understand the process of finding the decimal representation, though using a calculator provides the quickest and most accurate result.
Having the decimal representation of \( \sqrt{60} \) allows for easy integration into mathematical equations, scientific calculations, and various engineering problems, demonstrating its practical utility.
Simplified Radical Form of Square Root of 60
The square root of 60 can be expressed in a simplified radical form, which makes it easier to understand and use in various mathematical contexts. To simplify \( \sqrt{60} \), we start by breaking down the number 60 into its prime factors.
Step-by-Step Simplification
Here is the step-by-step process to simplify \( \sqrt{60} \):
- Factorize 60: Begin by finding the prime factors of 60. The prime factorization of 60 is: \[ 60 = 2^2 \times 3 \times 5 \]
- Group the factors: Identify pairs of prime factors. In this case, we have \( 2^2 \) as a pair: \[ 60 = (2^2) \times 3 \times 5 \]
- Simplify the square root: Take the square root of each pair and simplify. The square root of \( 2^2 \) is 2: \[ \sqrt{60} = \sqrt{(2^2) \times 3 \times 5} = \sqrt{2^2} \times \sqrt{3} \times \sqrt{5} = 2 \sqrt{15} \]
Therefore, the simplified radical form of \( \sqrt{60} \) is:
\[
\sqrt{60} = 2 \sqrt{15}
\]
Why Simplify?
Simplifying the square root of 60 to \( 2 \sqrt{15} \) has several benefits:
- Easier Manipulation: Simplified forms are easier to work with in algebraic expressions and equations.
- Clearer Understanding: It provides a clearer understanding of the relationship between the number and its factors.
- Consistency: Simplified radical forms are often preferred in mathematical conventions and standardized tests.
Understanding and using the simplified radical form of square roots, such as \( \sqrt{60} = 2 \sqrt{15} \), enhances mathematical problem-solving skills and provides a deeper insight into the properties of numbers.

Methods to Calculate Square Root of 60
Calculating the square root of 60 can be approached through various methods, each providing a different level of accuracy and understanding. Here, we explore four common methods: prime factorization, long division, using a calculator, and Newton's method.
1. Prime Factorization
This method involves breaking down the number 60 into its prime factors and simplifying the radical expression:
- Factorize 60: \[ 60 = 2^2 \times 3 \times 5 \]
- Simplify the square root: \[ \sqrt{60} = \sqrt{2^2 \times 3 \times 5} = 2 \sqrt{15} \]
This gives the simplified radical form \( 2 \sqrt{15} \).
2. Long Division Method
The long division method provides a step-by-step approach to approximate the square root:
- Estimate an initial value: Determine that \( \sqrt{60} \) is between 7 and 8, since \( 7^2 = 49 \) and \( 8^2 = 64 \).
- Set up the division: Place 60 under the long division symbol and find the largest number whose square is less than 60.
- Calculate the digits: Continue the process to refine the approximation to the desired decimal places.
Through this method, \( \sqrt{60} \) can be approximated to several decimal places.
3. Using a Calculator
The most straightforward way to find \( \sqrt{60} \) is by using a scientific calculator:
- Enter 60.
- Press the square root (√) button.
- The display will show approximately 7.745966692414834.
This method provides an accurate result quickly and easily.
4. Newton's Method
Newton's method, also known as the Newton-Raphson method, is an iterative approach to approximate the square root:
- Choose an initial guess: Start with a close estimate, such as 7.7.
- Apply the formula: \[ x_{n+1} = \frac{1}{2} \left( x_n + \frac{60}{x_n} \right) \]
- Iterate: Continue iterating until the difference between successive values is minimal.
This method converges quickly to the accurate value of \( \sqrt{60} \).
These methods provide different ways to understand and calculate the square root of 60, each offering unique insights and levels of precision. Whether using a calculator for quick results or applying more detailed methods for deeper understanding, knowing how to find \( \sqrt{60} \) is a valuable mathematical skill.
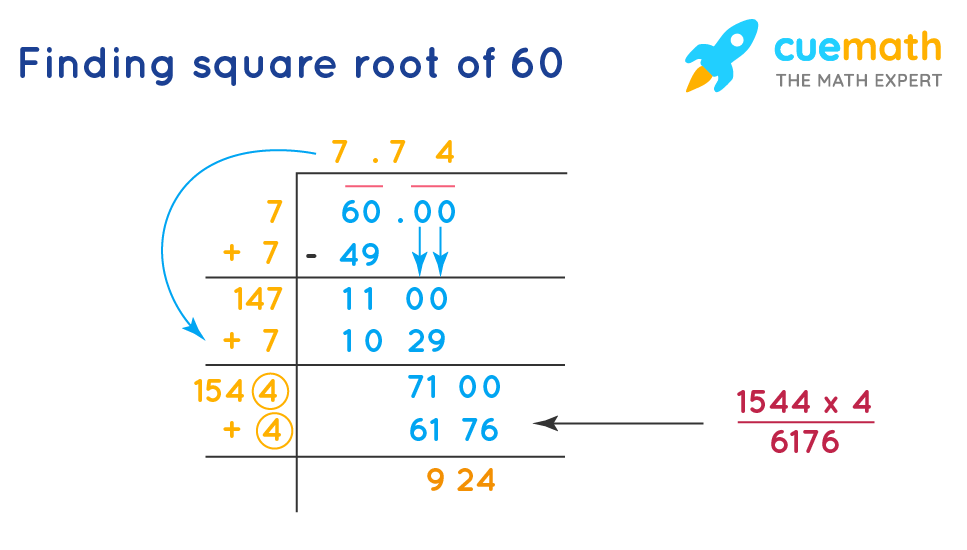
Long Division Method
The long division method is a manual technique used to find the square root of a number by approximating the digits step-by-step. Here’s a detailed guide to using the long division method to calculate the square root of 60:
Step-by-Step Process
- Setup: Write 60 as 60.000000 to accommodate several decimal places. Draw a division bar (like in long division) over the number.
- Initial Guess: Determine that \( \sqrt{60} \) is between 7 and 8 because \( 7^2 = 49 \) and \( 8^2 = 64 \). Start with 7 as the initial digit.
- Divide:
- Write 7 below the division bar and square it (7 * 7 = 49).
- Subtract 49 from 60, resulting in 11.
- Bring down two zeros, making it 1100.
- Double the Quotient: Double the current quotient (7) to get 14. Write 14 below the division bar.
- Find the Next Digit:
- Find a digit \( x \) such that \( 14x \cdot x \leq 1100 \).
- The digit 7 works because \( 147 \cdot 7 = 1029 \).
- Place 7 next to 14 and above the division bar. The quotient is now 77.
- Subtract 1029 from 1100 to get 71.
- Bring down two more zeros to get 7100.
- Repeat:
- Double the quotient (77) to get 154. Write 154 below the division bar.
- Find a digit \( y \) such that \( 154y \cdot y \leq 7100 \).
- The digit 4 works because \( 1544 \cdot 4 = 6176 \).
- Place 4 next to 154 and above the division bar. The quotient is now 774.
- Subtract 6176 from 7100 to get 924.
- Bring down two more zeros to get 92400.
- Continue: Continue the process until the desired precision is reached. The quotient approximates \( \sqrt{60} \).
Example Calculation
Following these steps, we find that:
\[
\sqrt{60} \approx 7.745
\]
This method, though lengthy, provides a clear and precise way to manually calculate square roots, reinforcing understanding of the concept.
Newton's Method
Newton's Method, also known as the Newton-Raphson Method, is an efficient iterative technique to approximate the square root of a number. Here's a step-by-step guide to using Newton's Method to find the square root of 60.
-
Start with an initial guess, \( x_0 \). A good starting point can be \( x_0 = 7 \) since \( 7^2 = 49 \) is close to 60.
-
Apply the Newton's iteration formula:
\[
x_{n+1} = \frac{1}{2} \left( x_n + \frac{60}{x_n} \right)
\] -
Repeat the iteration until the difference between successive approximations is smaller than a desired tolerance level. Let's go through a few iterations:
- First iteration (\( n = 0 \)):
\[
x_1 = \frac{1}{2} \left( 7 + \frac{60}{7} \right) = \frac{1}{2} \left( 7 + 8.5714 \right) = \frac{1}{2} \left( 15.5714 \right) = 7.7857
\] - Second iteration (\( n = 1 \)):
\[
x_2 = \frac{1}{2} \left( 7.7857 + \frac{60}{7.7857} \right) = \frac{1}{2} \left( 7.7857 + 7.7085 \right) = \frac{1}{2} \left( 15.4942 \right) = 7.7471
\] - Third iteration (\( n = 2 \)):
\[
x_3 = \frac{1}{2} \left( 7.7471 + \frac{60}{7.7471} \right) = \frac{1}{2} \left( 7.7471 + 7.7453 \right) = \frac{1}{2} \left( 15.4924 \right) = 7.7462
\]
- First iteration (\( n = 0 \)):
-
Continue the process until the difference between \( x_n \) and \( x_{n+1} \) is sufficiently small. After a few more iterations, the value stabilizes, and we get a more accurate approximation of the square root of 60.
Using Newton's Method, the square root of 60 can be approximated as \( \sqrt{60} \approx 7.746 \).
Using a Calculator
Using a calculator to find the square root of 60 is a straightforward process. Here are the detailed steps to do it:
-
Turn on your calculator.
-
Locate the square root function. This is usually represented by the symbol \( \sqrt{\ } \) or may be accessed by pressing a "2nd" or "shift" key followed by the \( x^2 \) key, depending on your calculator model.
-
Enter the number 60. You can do this by pressing the keys in sequence: 6 followed by 0.
-
Press the square root key (\( \sqrt{\ } \)) to compute the square root. The display should now show the result.
-
Read the result from the calculator display. The square root of 60 is approximately:
\[
\sqrt{60} \approx 7.745966692
\]
For most practical purposes, you can round this result to a desired number of decimal places. Commonly, it is rounded to two decimal places:
\[
\sqrt{60} \approx 7.75
\]
Using a calculator simplifies the process of finding the square root of 60, providing a quick and accurate result.
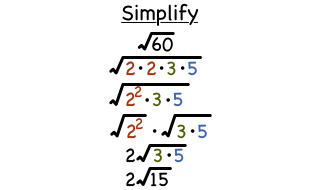
Applications of Square Root of 60
The square root of 60 (\(\sqrt{60} \approx 7.745966692414834\)) has several practical applications across various fields. Here, we explore its use in geometry, physics, and engineering.
Geometry Applications
In geometry, the square root of 60 is often used in calculations involving polygons and triangles. For example:
- Diagonal Lengths: It is used to find the lengths of diagonals in polygons, especially in rectangles and squares. For instance, the diagonal of a rectangle with sides of length 4 and 15 can be calculated using the formula \( \sqrt{4^2 + 15^2} = \sqrt{16 + 225} = \sqrt{241} \approx 15.524\).
- Special Triangles: In right-angled triangles, especially those with sides that form a Pythagorean triple, the square root of 60 can be a side length. For example, a triangle with one leg of length \( \sqrt{60} \) and another leg of length \( \sqrt{15} \) will have a hypotenuse of 9.
Physics Applications
In physics, \(\sqrt{60}\) is important in wave mechanics and simple harmonic motion. For example:
- Oscillations: It helps determine the natural frequency, period, and amplitude of oscillations in systems like springs and pendulums. The formula for the period of a simple harmonic oscillator involves the square root of the mass and the spring constant, which can include values like \(\sqrt{60}\).
- Wave Mechanics: The square root of 60 can appear in equations describing wave properties such as velocity and wavelength.
Engineering Applications
In engineering, \(\sqrt{60}\) is used in various calculations, such as:
- Unit Conversions: It is involved in converting units, especially in calculations involving area and volume.
- AC Power Calculations: The square root of 60 is used in electrical engineering to calculate properties of alternating current (AC) circuits, such as impedance and reactance.
Practical Examples
Let's look at a couple of practical examples:
- Rectangular Floor Painting: A salesman wants to build a rectangular floor garage with a length of 20 feet and a width of \(10\sqrt{60}\) feet. The area of the floor is \(20 \times 10\sqrt{60} = 200\sqrt{60} \approx 1549\) square feet. If painting costs $2 per square foot, the total cost will be \(1549 \times 2 = $3098\).
- Car Travel Distance: A car traveling at a speed of \(6\sqrt{240}\) miles per hour will cover a distance of \(185.88\) miles in 2 hours, calculated using the speed formula \( \text{Distance} = \text{Speed} \times \text{Time}\).
Understanding these applications is essential for solving complex problems and designing efficient systems in various scientific and engineering fields.
Geometry Applications
The square root of 60, approximately 7.746, finds various applications in geometry, particularly in calculations involving right triangles, circles, and other geometric shapes.
Right Triangles
In right triangles, the square root of 60 can be used to determine the length of a side when the hypotenuse or other sides are known. Using the Pythagorean theorem \(a^2 + b^2 = c^2\), where \(c\) is the hypotenuse:
- If one leg (\(a\)) is 6 and the other leg (\(b\)) is unknown, and the hypotenuse (\(c\)) is √60, then:
- \(6^2 + b^2 = (√60)^2\)
- \(36 + b^2 = 60\)
- \(b^2 = 60 - 36\)
- \(b^2 = 24\)
- \(b = √24 \approx 4.899\)
Circles
The square root of 60 is also useful in circle-related calculations, such as determining the radius or diameter of a circle when the area or circumference is known. For example:
- If the area of a circle is 60π square units, the radius (\(r\)) can be found using the formula \(A = πr^2\):
- \(60π = πr^2\)
- \(r^2 = 60\)
- \(r = √60 \approx 7.746\)
Regular Polygons
The square root of 60 can be applied to find the side length or diagonal of regular polygons. For instance, in a regular hexagon where the distance between opposite vertices (a diagonal) is known to be √60:
- The side length (\(s\)) can be calculated based on the properties of hexagons:
- Diagonal of a regular hexagon = 2 × side length
- So, \(√60 = 2s\)
- \(s = √60 / 2 \approx 3.873\)
Volumes and Areas
In 3D geometry, the square root of 60 can be used to calculate various measurements, such as the edge length of a cube with a given volume or the side length of a square base in a rectangular prism:
- If a cube has a volume of \(60 \text{ cubic units}\), the edge length (\(a\)) can be found using \(V = a^3\):
- \(a = (√60)^{1/3} \approx 3.914\)
Physics Applications
The square root of 60, approximately \( \sqrt{60} \approx 7.75 \), finds several applications in physics, particularly in calculations involving wave phenomena, electrical circuits, and mechanics. Here are some detailed examples of its usage:
-
Wave Phenomena:
In the study of wave mechanics, the wavelength (\( \lambda \)) and frequency (\( f \)) of waves are often related through the wave speed (\( v \)). For certain calculations, especially when dealing with non-standard frequencies, using the square root of 60 can simplify the computation of these relationships.
-
Electrical Circuits:
In alternating current (AC) circuits, the root mean square (RMS) values of current and voltage are used extensively. The RMS value of a sinusoidal current is given by \( I_{\text{RMS}} = \frac{I_0}{\sqrt{2}} \). In complex circuit calculations, the square root of values like 60 may appear when calculating impedances and phase angles in RLC circuits (resistor-inductor-capacitor circuits).
-
Mechanics and Dynamics:
In physics problems involving rotational motion, moment of inertia (\( I \)) is a crucial parameter. For instance, for a system where the combined inertia of multiple objects needs to be calculated, the square root of sums involving values like 60 can be significant. This appears in equations related to angular momentum (\( L = I \omega \)) and kinetic energy of rotating systems (\( K = \frac{1}{2} I \omega^2 \)).
Understanding these applications highlights the importance of the square root of 60 in simplifying and solving various physical equations, ensuring accurate and efficient results in practical scenarios.
Engineering Applications
The square root of 60, approximately 7.75, is used in various engineering applications to solve practical problems. Here are a few examples:
1. Structural Engineering
In structural engineering, the natural frequency of a structure is crucial for understanding its response to dynamic loads such as wind, earthquakes, or traffic on bridges. The natural frequency (f) of a structure can be approximated using the formula:
\( f = \frac{1}{2\pi} \sqrt{\frac{k}{m}} \)
where \( k \) is the stiffness of the structure and \( m \) is its mass. If the stiffness or mass involves the number 60, its square root will play a role in calculating the natural frequency.
2. Electrical Engineering
In electrical engineering, square roots are often used to calculate the root mean square (RMS) values of alternating current (AC) signals. The RMS value provides a measure of the effective power of the signal. For example, the RMS value of a sinusoidal AC current \( I(t) = I_0 \sin(\omega t) \) is given by:
\( I_{RMS} = \frac{I_0}{\sqrt{2}} \)
Calculations involving circuits with resistances or reactances related to 60 ohms may require the square root of 60 for accurate RMS computations.
3. Mechanical Engineering
In mechanical engineering, particularly in vibration analysis, the square root of 60 can be used to determine the critical speeds of rotating machinery. The critical speed (\( n_c \)) is determined by the equation:
\( n_c = \sqrt{\frac{k}{m}} \)
where \( k \) is the stiffness and \( m \) is the mass of the rotating component. Accurate calculation of critical speeds ensures the machinery operates safely and efficiently.
4. Control Systems
Control systems engineering uses square roots in designing systems with specific damping ratios and natural frequencies. The damping ratio (\( \zeta \)) and natural frequency (\( \omega_n \)) are key parameters in the second-order differential equations that describe the system dynamics:
\( \omega_n = \sqrt{\frac{k}{m}} \)
Here, if the system parameters include 60, the square root of 60 will be essential in determining the system's performance characteristics.
5. Fluid Mechanics
In fluid mechanics, the square root of 60 might be used in calculations involving the Reynolds number (Re), which determines the flow regime (laminar or turbulent) of a fluid. The formula for Reynolds number is:
\( Re = \frac{\rho vL}{\mu} \)
If a problem involves a parameter value of 60, the square root of 60 could be part of solving for critical velocities or dimensions in fluid flow.
These examples demonstrate the importance of the square root of 60 in various engineering disciplines, ensuring accurate and efficient design and analysis of systems and structures.

Estimating the Square Root of 60
Estimating the square root of 60 can be approached through several methods to find a close approximation. Here, we will explore two common methods: the decimal method and the closest perfect square method.
The Decimal Method
The decimal method involves finding the nearest perfect square to 60 and then estimating the decimal part of the answer. Here are the steps:
- Identify the nearest perfect squares around 60. These are 49 (72) and 64 (82).
- Since 60 is closer to 64, we start with the approximation that the square root of 60 is slightly less than 8.
- To refine the estimate, we can interpolate. The difference between 60 and 64 is 4, and the difference between 64 and 49 is 15. Thus, the decimal part can be approximated by the ratio 4/15.
- Add this decimal to the whole number part: \( \sqrt{60} \approx 8 - \frac{4}{15} = 8 - 0.27 = 7.73 \).
The Closest Perfect Square Method
This method involves finding the two closest perfect squares to 60 and estimating the answer based on the relationship between these perfect squares.
- Find the two closest perfect squares: 49 and 64.
- Estimate the position of 60 between these two squares. Since 60 is closer to 64, we can use a weighted average approach.
- Calculate the fraction of the distance: \((60 - 49) / (64 - 49) = 11/15 \approx 0.73\).
- Combine this fraction with the square root values: \( 7 + 0.73 \approx 7.73 \).
Both methods provide a similar estimate, with \( \sqrt{60} \approx 7.73 \). These estimations are useful for quick calculations when precision is not crucial, and they demonstrate the practical applications of understanding square roots.
Comparing Square Roots of Nearby Numbers
Understanding how the square root of 60 compares to the square roots of nearby numbers can provide valuable insights into its relative size and properties. Here's a detailed comparison:
- Square Root of 49: The square root of 49 is exactly 7 since \( 7^2 = 49 \).
- Square Root of 60: The square root of 60 is approximately \( 7.7459666924 \), which lies between the square roots of 49 and 64.
- Square Root of 64: The square root of 64 is exactly 8 since \( 8^2 = 64 \).
Thus, it is evident that:
\( 7 < \sqrt{60} < 8 \)
To further illustrate, here is a comparison of the square roots of numbers around 60:
| Number | Square Root |
|---|---|
| 49 | 7 |
| 50 | Approximately 7.071 |
| 59 | Approximately 7.681 |
| 60 | Approximately 7.746 |
| 61 | Approximately 7.810 |
| 64 | 8 |
As shown in the table, the square root of 60 is closer to 8 than it is to 7, reflecting its position between the two integers.
Such comparisons help in estimating square roots and understanding the properties of irrational numbers, as the square root of 60 cannot be expressed as a simple fraction and is an irrational number. This comparative approach is useful in various applications across mathematics, physics, and engineering.
Prime Factorization Method
The prime factorization method is a useful technique for simplifying the square root of a number by breaking it down into its prime factors. Here, we will find the square root of 60 using this method.
-
Step 1: Prime Factorization of 60
First, we need to express 60 as a product of its prime factors:
60 = 2 × 2 × 3 × 5
-
Step 2: Pair the Prime Factors
Next, we group the prime factors into pairs. Since 60 = 22 × 3 × 5, we have one pair of 2s:
- Pair of 2s: 22
- Unpaired factors: 3 and 5
-
Step 3: Simplify the Square Root
Take the square root of each pair and multiply them outside the radical sign:
\(\sqrt{60} = \sqrt{2^2 \times 3 \times 5} = 2 \times \sqrt{3 \times 5}\)
-
Step 4: Combine and Simplify
Combine the results to get the simplified form:
\(\sqrt{60} = 2\sqrt{15}\)
Therefore, the square root of 60 in its simplified radical form is \(2\sqrt{15}\).
Practical Examples Involving Square Root of 60
The square root of 60, approximately equal to 7.746, appears in various practical scenarios. Here, we will explore some examples in different fields such as geometry, physics, and engineering.
-
Example 1: Geometry - Finding the Hypotenuse
In a right triangle, if the lengths of the legs are 6 and 4 units, we can use the Pythagorean theorem to find the hypotenuse:
\( \text{Hypotenuse}^2 = 6^2 + 4^2 \)
\( \text{Hypotenuse}^2 = 36 + 16 = 52 \)
\( \text{Hypotenuse} = \sqrt{52} \approx 7.211 \)
To get a more precise hypotenuse length, consider adjusting the leg lengths to 5 and 5, giving:
\( \text{Hypotenuse}^2 = 5^2 + 5^2 = 25 + 25 = 50 \)
\( \text{Hypotenuse} = \sqrt{50} = 5\sqrt{2} \approx 7.071 \)
-
Example 2: Physics - Calculating Speed
Imagine a particle moving in a straight line. If its displacement in meters over time is given by \( s(t) = 60 \) meters, and it took \( t = 7.746 \) seconds to cover this distance, the average speed \( v \) can be calculated as:
\( v = \frac{s}{t} = \frac{60}{7.746} \approx 7.746 \text{ m/s} \)
-
Example 3: Engineering - Material Strength
In engineering, knowing the square root of certain values helps in calculating stress and strain on materials. For example, if a metal rod is subjected to a force that produces a deformation proportional to \( \sqrt{60} \), this deformation value (approximately 7.746) is crucial in assessing whether the material can withstand the applied force without yielding.
These examples illustrate how the square root of 60 is utilized across different domains, demonstrating its practical importance and application.

Common Misconceptions About Square Roots
Square roots are often misunderstood, leading to several common misconceptions. Clarifying these can help in a better understanding of mathematical principles involving square roots.
-
Misconception 1: Square Roots Are Always Rational Numbers
Many believe that the square root of any number is always a rational number. However, this is not true. For instance, the square root of 60 is irrational:
\(\sqrt{60} \approx 7.746\)
This number cannot be expressed as a fraction of two integers, making it an irrational number.
-
Misconception 2: Square Root of a Negative Number Is Undefined
Another common misconception is that the square root of a negative number does not exist. In fact, while it is not a real number, it is defined in the set of complex numbers:
\(\sqrt{-1} = i\)
Where \(i\) is the imaginary unit. Thus, for any negative number \(-a\), the square root is:
\(\sqrt{-a} = i\sqrt{a}\)
-
Misconception 3: The Square Root Function Is Always Positive
People often think that the square root of a number is always positive. While the principal square root is positive, every positive number actually has two square roots: one positive and one negative:
For example, \(\sqrt{60} \approx 7.746\) and \(-\sqrt{60} \approx -7.746\).
-
Misconception 4: Squaring and Square Rooting Are Perfectly Inverse Operations
It is a common belief that squaring and taking the square root are perfectly inverse operations. While they are inverse operations, the square root function returns only the principal (non-negative) root. Thus:
\(\sqrt{49} = 7\) but \((-7)^2 = 49\)
However, \(\sqrt{49}\) does not equal -7.
Understanding these misconceptions can deepen one’s comprehension of square roots and their properties.
Visualizing the Square Root of 60
Visualizing the square root of 60 can help in understanding its magnitude and properties. Here, we will use geometric representation and number lines for better visualization.
-
Geometric Representation
One way to visualize the square root of 60 is by using a square. If we create a square with an area of 60 square units, the length of each side of the square will be the square root of 60:
\(\text{Area} = 60 \, \text{square units} \)
\(\text{Side length} = \sqrt{60} \approx 7.746 \, \text{units} \)
This means each side of the square will measure approximately 7.746 units.
-
Number Line Representation
Another effective method is to place \(\sqrt{60}\) on a number line. We know that \(\sqrt{60}\) is between 7 and 8 because:
\(7^2 = 49\) and \(8^2 = 64\)
Thus, \(\sqrt{60}\) lies closer to 8:
\(7.7^2 = 59.29\)
\(7.8^2 = 60.84\)
So, \(\sqrt{60} \approx 7.746\), and can be marked between 7.7 and 7.8 on the number line.
-
Graphical Representation
Using a graph, plot the function \(y = \sqrt{x}\). The value of \(\sqrt{60}\) can be found by locating the point where \(x = 60\) and reading the corresponding \(y\) value:
Plot the function from \(x = 0\) to \(x = 70\).
At \(x = 60\), \(y \approx 7.746\).
This visual aid helps in understanding the growth rate of the square root function and where \(\sqrt{60}\) fits in the context of other square roots.
These methods provide a clear visualization of \(\sqrt{60}\), enhancing comprehension through geometric, numerical, and graphical perspectives.
Video hướng dẫn đơn giản hóa căn bậc hai của 60, giúp bạn hiểu rõ hơn về khái niệm này.
Đơn Giản Hóa Căn Bậc Hai của 60: Sqrt(60)
READ MORE:
Video giải thích chi tiết về căn bậc hai của 60, giúp bạn nắm rõ khái niệm này.
Căn Bậc Hai của 60