Topic what is the square root of 640: Discover the fascinating world of square roots as we explore the square root of 640. Learn how to calculate it, understand its exact value in simplified form, and uncover its decimal approximation. This comprehensive guide will also delve into practical applications, ensuring you grasp the importance of this mathematical concept in everyday life.
Table of Content
- Square Root of 640
- Introduction to Square Roots
- Understanding the Concept of Square Roots
- Mathematical Definition and Notation
- Calculating the Square Root of 640
- Prime Factorization Method
- Simplified Radical Form
- Steps to Simplify the Square Root of 640
- Applications of Square Roots
- Geometry and Measurement
- Physics and Engineering
- Square Roots in Everyday Life
- Using Calculators to Find Square Roots
- Common Mistakes to Avoid
- Summary and Conclusion
- YOUTUBE: Video này giải thích cách tính căn bậc hai của 640, cung cấp các ví dụ và ứng dụng thực tế.
Square Root of 640
The square root of a number is a value that, when multiplied by itself, gives the original number. In this case, we are looking for the square root of 640.
Exact Value
The exact value of the square root of 640 can be expressed in its simplest radical form:
\[ \sqrt{640} = 8\sqrt{10} \]
Decimal Approximation
To find a decimal approximation of the square root of 640, you can use a calculator. The approximate value is:
\[ \sqrt{640} \approx 25.2982 \]
Steps to Simplify the Square Root
- Factorize 640 into its prime factors:
- 640 = 2 \times 320
- 320 = 2 \times 160
- 160 = 2 \times 80
- 80 = 2 \times 40
- 40 = 2 \times 20
- 20 = 2 \times 10
- 10 = 2 \times 5
- Group the prime factors into pairs:
- 640 = 2^7 \times 5
- Simplify the square root by taking out pairs of prime factors:
- \[ \sqrt{640} = \sqrt{2^7 \times 5} = \sqrt{(2^3 \times 2) \times 5} = 2^3 \sqrt{10} = 8\sqrt{10} \]
Applications
Knowing the square root of a number like 640 can be useful in various mathematical and practical applications, such as:
- Geometry and measurement, for finding the lengths of sides in right triangles or other shapes.
- Physics, for calculating distances or magnitudes.
- Engineering, for determining material properties and dimensions.
| Square Root | Value |
| Exact | 8\sqrt{10} |
| Approximate | 25.2982 |

READ MORE:
Introduction to Square Roots
The concept of square roots is fundamental in mathematics, representing a number that, when multiplied by itself, yields the original number. Understanding square roots is crucial for various mathematical computations and real-world applications.
For instance, the square root of a number \( x \) is a value \( y \) such that \( y^2 = x \). In mathematical notation, this is expressed as:
\[ y = \sqrt{x} \]
Square roots can be applied to perfect squares (such as 4, 9, 16, etc.) which have whole number roots, or non-perfect squares (such as 2, 3, 5, etc.) which have irrational number roots. Here's a list of some basic square roots:
- \(\sqrt{4} = 2\)
- \(\sqrt{9} = 3\)
- \(\sqrt{16} = 4\)
- \(\sqrt{25} = 5\)
When dealing with non-perfect squares, we often approximate the square roots. For example, the square root of 2 is approximately 1.414. These approximations are often sufficient for practical purposes in fields such as engineering, physics, and everyday calculations.
Understanding square roots also extends to recognizing their properties and behavior in different mathematical operations. For example:
- The square root of a product is the product of the square roots: \(\sqrt{ab} = \sqrt{a} \times \sqrt{b}\)
- The square root of a quotient is the quotient of the square roots: \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
Square roots are not only a cornerstone in algebra but also play a vital role in higher mathematics, including calculus and complex numbers. Mastery of square roots paves the way for deeper mathematical understanding and problem-solving abilities.
Understanding the Concept of Square Roots
The concept of a square root is fundamental in mathematics. The square root of a number is a value that, when multiplied by itself, gives the original number. Mathematically, the square root of a number x is denoted as √x, which implies:
\[
\sqrt{x} = q \implies q \times q = x \quad \text{or} \quad q^2 = x
\]
For example, the square root of 640 is a number which, when squared, equals 640:
\[
\sqrt{640} \times \sqrt{640} = 640 \quad \text{or} \quad (\sqrt{640})^2 = 640
\]
Square roots can be categorized into two types: perfect squares and non-perfect squares. A perfect square is a number whose square root is an integer. For instance, 16 is a perfect square because its square root is 4, an integer. Conversely, 640 is not a perfect square because its square root is not an integer.
Square roots are also classified as either rational or irrational numbers. A rational number can be expressed as a fraction of two integers, while an irrational number cannot. Since the square root of 640 is approximately 25.298, which cannot be expressed as a fraction of two integers, it is an irrational number.
The principal (positive) square root of 640 is represented as:
\[
\sqrt{640} \approx 25.298
\]
To further illustrate, here are some properties of square roots:
- Not a Perfect Square: The square root of 640 is approximately 25.298, indicating it is not a perfect square.
- Rational vs. Irrational: Since 25.298 cannot be expressed as a simple fraction, √640 is irrational.
Square roots are widely used in various fields such as geometry, where they are used to find the lengths of sides in right triangles, and in physics and engineering to solve problems involving areas and volumes.
Mathematical Definition and Notation
The square root of a number is a value that, when multiplied by itself, gives the original number. For any positive number \( x \), its square root is denoted as \( \sqrt{x} \). This operation is the inverse of squaring a number. For example, the square root of 25 is 5 because \( 5 \times 5 = 25 \). This relationship can be expressed as:
\[ \sqrt{25} = 5 \]
Square roots can also be represented using exponentiation. The square root of \( x \) is equivalent to raising \( x \) to the power of one-half:
\[ \sqrt{x} = x^{1/2} \]
Numbers can be categorized as either perfect squares or non-perfect squares based on their square roots. A perfect square has an integer as its square root, while a non-perfect square does not. For instance:
- \( \sqrt{16} = 4 \) (Perfect square)
- \( \sqrt{20} \approx 4.472 \) (Non-perfect square)
The square root symbol \( \sqrt{} \) is called a radical, and the number inside the symbol is known as the radicand. When discussing square roots, it's important to consider both the principal (positive) root and the negative root. For example, the square roots of 25 are +5 and -5, since both satisfy the equation \( x^2 = 25 \):
\[ \sqrt{25} = \pm 5 \]
For the square root of 640, the exact value is:
\[ \sqrt{640} = 25.298221281347 \]
Since this is not a whole number, 640 is not a perfect square. Furthermore, because the square root of 640 is a non-terminating and non-repeating decimal, it is classified as an irrational number.
To summarize:
- The square root of 640 can be expressed as \( \sqrt{640} \) or \( 640^{1/2} \).
- Its approximate decimal form is 25.298.
- Since it is not an integer, 640 is not a perfect square.
- The square root of 640 is irrational.
Calculating the Square Root of 640
Calculating the square root of 640 involves a few different methods. Here, we will discuss the prime factorization method and the long division method, which can help us understand and approximate the square root of 640.
Prime Factorization Method
Prime factorization involves breaking down the number 640 into its prime factors:
- First, factorize 640: \( 640 = 2^7 \times 5 \)
- Next, we take the square root of both sides: \( \sqrt{640} = \sqrt{2^7 \times 5} \)
- We can simplify this to: \( \sqrt{640} = \sqrt{2^6 \times 2 \times 5} = 8\sqrt{10} \)
The simplified radical form of the square root of 640 is \( 8\sqrt{10} \).
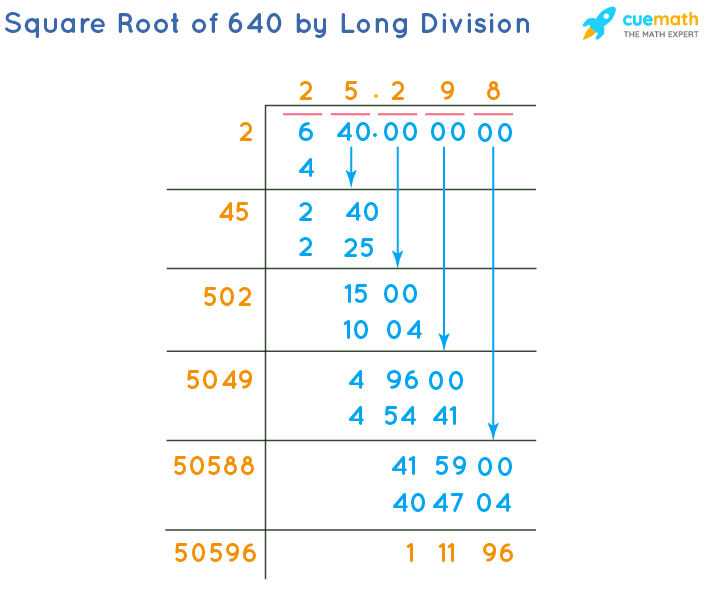
Long Division Method
The long division method provides a decimal approximation of the square root of 640:
- Set up the number in pairs of digits from right to left: \( 640.000000 \).
- Find the largest number whose square is less than or equal to 640. Here, it is 25 because \( 25^2 = 625 \).
- Subtract 625 from 640 to get the remainder 15. Bring down the next pair of zeros to get 1500.
- Double the quotient (25) to get 50, and find a digit to place next to 50 to form a number that, when multiplied by the same digit, is less than or equal to 1500. This digit is 2, making it 502. \( 502 \times 2 = 1004 \).
- Continue this process to obtain more decimal places as needed.
Using this method, the square root of 640 is approximately 25.29822.
Using Calculators
You can also use calculators or software like Excel or Google Sheets to find the square root of 640. Simply enter =SQRT(640) in a cell to get the result.
Overall, the square root of 640 is an irrational number, approximately 25.298, and can also be expressed in simplified radical form as \( 8\sqrt{10} \).

Prime Factorization Method
The prime factorization method is a way to simplify the square root of a number by expressing it as a product of its prime factors. This method involves the following steps:
- First, find the prime factors of the number. For 640, the prime factorization is:
- Next, group the factors in pairs of two. Each pair will come out from under the square root:
- Take one factor from each pair out of the square root:
- Multiply the factors that were taken out of the square root:
\(640 = 2^7 \times 5\)
\(640 = (2^2 \times 2^2 \times 2^2) \times (2 \times 5)\)
\(\sqrt{640} = \sqrt{(2^2 \times 2^2 \times 2^2) \times (2 \times 5)} = 2 \times 2 \times 2 \times \sqrt{10}\)
\(\sqrt{640} = 8\sqrt{10}\)
Therefore, the simplified radical form of the square root of 640 is \(8\sqrt{10}\).
This method is particularly useful as it helps to simplify complex square roots into more manageable forms, making it easier to work with them in various mathematical problems.
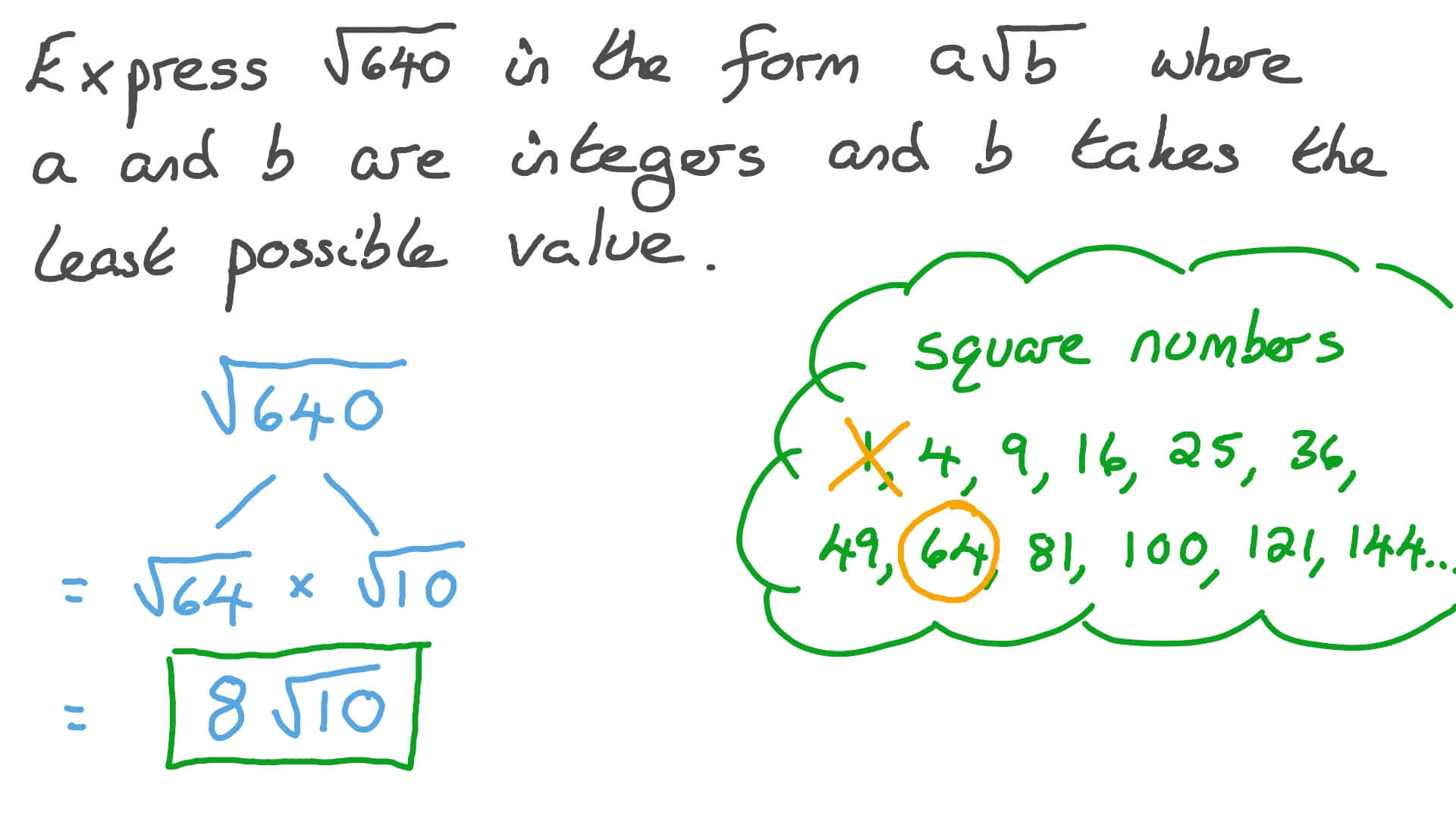
Simplified Radical Form
The square root of 640 can be simplified using prime factorization. The goal is to express 640 in terms of its prime factors and then simplify the square root based on these factors. Here is a step-by-step guide:
- First, find the prime factorization of 640:
\(640 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 5 = 2^7 \times 5\)
- Group the factors into pairs:
\(2^7 = (2^3)^2 \times 2 = 8^2 \times 2\)
- Simplify the square root by taking one factor from each pair:
\(\sqrt{640} = \sqrt{2^7 \times 5} = \sqrt{(2^3)^2 \times 2 \times 5} = \sqrt{8^2 \times 10} = 8\sqrt{10}\)
Thus, the simplified radical form of the square root of 640 is \(8\sqrt{10}\).
For clarity, here's the breakdown in a table:
| Step | Calculation |
|---|---|
| Prime Factorization | \(640 = 2^7 \times 5\) |
| Group into pairs | \((2^3)^2 \times 2 \times 5\) |
| Simplify | \(8^2 \times 10\) |
| Square Root | \(8\sqrt{10}\) |
Therefore, the square root of 640 in its simplest radical form is \(8\sqrt{10}\), which is approximately equal to 25.298 in decimal form.
Steps to Simplify the Square Root of 640
The square root of 640 can be simplified by using the prime factorization method. Here are the detailed steps to simplify it:
First, find the prime factors of 640. To do this, continuously divide 640 by its smallest prime factor until you reach 1.
- 640 ÷ 2 = 320
- 320 ÷ 2 = 160
- 160 ÷ 2 = 80
- 80 ÷ 2 = 40
- 40 ÷ 2 = 20
- 20 ÷ 2 = 10
- 10 ÷ 2 = 5
- 5 ÷ 5 = 1
Express 640 as the product of its prime factors:
\[ 640 = 2^7 \times 5^1 \]
Group the factors in pairs:
\[ 640 = (2^2 \times 2^2 \times 2^2) \times (2 \times 5) \]
Take one factor from each pair outside the square root:
\[ \sqrt{640} = \sqrt{(2^2) \times (2^2) \times (2^2) \times (2 \times 5)} \]
\[ \sqrt{640} = 2 \times 2 \times 2 \times \sqrt{2 \times 5} \]
Simplify the expression:
\[ \sqrt{640} = 8 \sqrt{10} \]
Therefore, the simplified radical form of the square root of 640 is:
\[ \sqrt{640} = 8 \sqrt{10} \]
Applications of Square Roots
Square roots have numerous practical applications across various fields. Understanding how square roots are used in real-world scenarios can enhance our comprehension of their importance and utility. Below are some key areas where square roots play a crucial role:
- Geometry: Square roots are essential in geometry for calculating distances, areas, and lengths. For instance, the length of the diagonal of a square can be found using the square root of the sum of the squares of its sides. The Pythagorean theorem also utilizes square roots to determine the length of the hypotenuse in right-angled triangles.
- Physics: In physics, square roots are used to calculate various quantities such as the speed of an object in free fall, the intensity of sound waves, and the energy of particles. For example, the time it takes for an object to fall to the ground from a certain height is proportional to the square root of the height.
- Finance: In finance, square roots are used in risk assessment and investment analysis. The volatility of a stock, which measures how much its price fluctuates, is often calculated using the square root of the variance of its returns. This helps investors evaluate the risk associated with different financial assets.
- Statistics: Square roots are integral to statistical analysis, particularly in calculating standard deviation, which measures the dispersion of a dataset. The standard deviation is the square root of the variance, providing insights into the spread of data points around the mean.
- Engineering: Engineers use square roots in various calculations, including determining the natural frequencies of structures, which is crucial for assessing their stability under different loads. In electrical engineering, square roots are used to calculate power, voltage, and current in circuits.
- Computer Science: In computer science, square roots are applied in algorithms for encryption, image processing, and computer graphics. For example, calculating the distance between two points in a coordinate system often involves finding the square root of the sum of the squares of the differences in their coordinates.
- Navigation: Pilots and navigators use square roots to compute distances between points on a map or globe. The distance formula, which involves the square root of the sum of the squares of differences in coordinates, helps in plotting accurate courses.
- Architecture: Architects use square roots to determine the dimensions and areas of various elements within their designs. This helps in creating accurate and proportionate structures.
By exploring these applications, we can see how fundamental the concept of square roots is to multiple disciplines and how it aids in solving practical problems.
Geometry and Measurement
Square roots have significant applications in geometry and measurement, particularly in calculating distances and areas. The square root of a number is crucial when dealing with geometric shapes and their properties. Here’s how the square root of 640 can be applied in geometry and measurement:
1. Diagonals of a Square
In a square, the diagonal length can be found using the formula:
\[ d = a \sqrt{2} \]
where \( d \) is the diagonal and \( a \) is the side length. For a square whose area is 640 square units, we can determine the side length:
\[ a = \sqrt{640} \]
Using the simplified radical form and the approximate decimal value:
\[ a \approx 25.3 \text{ units} \]
The diagonal \( d \) is then:
\[ d \approx 25.3 \times \sqrt{2} \approx 35.8 \text{ units} \]
2. Distance in the Coordinate Plane
In coordinate geometry, the distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) is given by the distance formula:
\[ \text{Distance} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
If the calculated distance is 640 units, the points lie at a distance:
\[ \sqrt{640} \approx 25.3 \text{ units} \]
3. Pythagorean Theorem
In a right triangle, the length of the hypotenuse \( c \) can be determined using the Pythagorean theorem:
\[ c = \sqrt{a^2 + b^2} \]
If \( a^2 + b^2 = 640 \), then:
\[ c = \sqrt{640} \approx 25.3 \text{ units} \]
This illustrates the use of the square root of 640 in determining the hypotenuse of a right triangle with appropriate leg lengths.
4. Area of Geometric Shapes
In some cases, the square root is used to find dimensions when the area is known. For instance, if the area of a square is 640 square units, the side length \( a \) is:
\[ a = \sqrt{640} \approx 25.3 \text{ units} \]
This demonstrates how square roots are essential in reverse calculations to find lengths from areas.
In summary, the square root of 640 plays an important role in various geometric and measurement applications, from determining side lengths and diagonals to calculating distances and applying the Pythagorean theorem.
Physics and Engineering
Square roots play a significant role in various aspects of physics and engineering. They are essential in calculations involving areas, volumes, and other geometric properties, as well as in solving differential equations and understanding waveforms. Here are some specific applications:
- Wave Mechanics: In physics, the square root function is often used to describe wave phenomena. For example, the intensity of a wave is proportional to the square of its amplitude. If you need to find the amplitude from the intensity, you take the square root of the intensity value.
- Electrical Engineering: In electrical engineering, the square root is used in calculating the root mean square (RMS) value of alternating current (AC) signals. The RMS value is crucial for determining the effective voltage or current of an AC circuit.
- Structural Engineering: When designing structures, engineers use the square root to calculate natural frequencies of vibration. The natural frequency is inversely proportional to the square root of the mass of the structure.
- Optics: The square root function is used in optics to relate the focal length of lenses to the curvature and refractive index of the lens material. This helps in designing lenses with desired focusing properties.
- Heat Transfer: In thermal engineering, the square root is used in the analysis of heat conduction problems. The rate of heat transfer can be related to the square root of time, especially in transient heat conduction.
Let's look at a specific example involving the square root of 640:
Suppose we are analyzing a physical system where the energy stored in a component is proportional to the square of a variable \( x \). If the energy stored is 640 units, we can find the value of \( x \) as follows:
\[
E = k x^2 \quad \text{where} \quad E = 640
\]
Solving for \( x \) we get:
\[
x = \sqrt{\frac{E}{k}}
\]
If \( k \) is 1 (for simplicity), then:
\[
x = \sqrt{640} \approx 25.30
\]
This calculation shows how the square root of 640 can be applied in determining a physical quantity in engineering contexts.
Square Roots in Everyday Life
Square roots are not just mathematical abstractions; they have practical applications in our daily lives. Here are some examples where square roots come into play:
- Cooking: When adjusting a recipe, square roots can help in scaling quantities. For instance, if you need to adjust a recipe to serve a different number of people, you can use square roots to proportionally increase or decrease ingredient amounts.
- Gardening: If you are planning to create a square garden bed with an area of 640 square feet, you can find the side length of the bed by taking the square root of 640. This helps in planning and optimizing the use of space.
- Real Estate: Square roots are used to determine the dimensions of a room or a plot of land. For example, if you know the area of a square plot is 640 square feet, the length of each side of the plot is \( \sqrt{640} \) feet, which is approximately 25.3 feet.
- Travel: When calculating distances, square roots are useful. For instance, the distance between two points in a city grid can be found using the Pythagorean theorem, which involves taking the square root of the sum of the squares of the differences in the x and y coordinates.
- Finance: In finance, square roots are used in various formulas, such as those calculating the volatility of stocks. The standard deviation, which is the square root of the variance, helps investors understand the risk associated with a particular investment.
- Construction: Builders and architects use square roots to determine dimensions and areas in their projects. For example, to ensure a room is square, they need to check that the diagonal measurement equals the square root of the sum of the squares of the room's length and width.
Let's explore a specific example involving the square root of 640 in everyday life:
Imagine you are creating a square patio with an area of 640 square feet. To find the length of each side of the patio, you would calculate:
\[
\text{Side length} = \sqrt{640} \approx 25.30 \text{ feet}
\]
This calculation helps you determine that each side of the square patio should be approximately 25.3 feet long.
These examples illustrate how understanding and using square roots can make everyday tasks easier and more efficient.
Using Calculators to Find Square Roots
Calculators are invaluable tools for finding square roots quickly and accurately. Whether you are using a physical calculator, a calculator app on your smartphone, or an online calculator, the process is straightforward. Here's a step-by-step guide on how to find the square root of 640 using different types of calculators:
- Using a Physical Calculator:
- Turn on the calculator.
- Press the square root (√) button.
- Enter the number 640.
- Press the equals (=) button to display the result.
- The calculator will show the square root of 640, which is approximately 25.298.
- Using a Smartphone Calculator App:
- Open the calculator app on your smartphone.
- Switch to scientific mode if necessary (this usually involves rotating the phone to landscape orientation).
- Press the square root (√) button.
- Enter the number 640.
- Press the equals (=) button to display the result.
- The app will show the square root of 640, which is approximately 25.298.
- Using an Online Calculator:
- Open your web browser and go to an online calculator website.
- Locate the square root function on the website interface.
- Enter the number 640 in the input field.
- Click the equals (=) button or press Enter to display the result.
- The website will show the square root of 640, which is approximately 25.298.
In all these methods, the square root function is represented by the symbol √. Here is the mathematical representation:
\[
\sqrt{640} \approx 25.298
\]
Using calculators to find square roots is efficient and eliminates the need for manual calculations, ensuring accuracy in your results.
Common Mistakes to Avoid
When calculating square roots, especially for non-perfect squares like 640, there are several common mistakes that people often make. Being aware of these can help ensure accurate results. Here are some mistakes to watch out for:
- Rounding Errors: One common mistake is rounding too early in the calculation process. It's important to carry more decimal places in intermediate steps and round only in the final result to avoid significant errors.
- Incorrect Use of the Calculator: Misusing calculator functions is another frequent mistake. Ensure you use the square root button (√) correctly and enter the number properly to get an accurate result.
- Misinterpreting the Result: Sometimes, people misinterpret the output of the calculator. For instance, they might confuse the square root with the original number or another value. Always double-check the context of your calculation.
- Forgetting the ± Sign: When solving equations that involve square roots, it's easy to forget that there are two solutions: a positive and a negative root. For example, both 25.298 and -25.298 are roots of 640, although in practical applications, the positive root is typically used.
- Ignoring Units: In applied problems, ignoring the units can lead to mistakes. Always include and check units in your calculations to ensure consistency and correctness.
- Misunderstanding Simplified Radical Form: When simplifying square roots, ensure you break down the number correctly. For example, \( \sqrt{640} \) can be simplified to \( 8\sqrt{10} \), but errors in factorization can lead to incorrect simplifications.
- Skipping Steps: In a rush to get the answer, it's easy to skip steps, leading to mistakes. Follow a methodical approach, especially for complex calculations.
To illustrate, let’s simplify the square root of 640 correctly:
Step 1: Factorize 640 into prime factors:
\[
640 = 2^7 \times 5
\]
Step 2: Apply the square root to each factor:
\[
\sqrt{640} = \sqrt{2^7 \times 5} = \sqrt{2^6 \times 2 \times 5} = 8 \sqrt{10}
\]
Thus, \( \sqrt{640} = 8\sqrt{10} \).
Avoiding these common mistakes will help you achieve accurate and reliable results when calculating square roots.
Summary and Conclusion
Understanding and calculating the square root of 640 has numerous practical applications across various fields such as physics, engineering, everyday life, and more. Here is a summary of the key points discussed:
- The square root of 640 is approximately 25.298, which can be expressed as \( \sqrt{640} \approx 25.298 \).
- Using calculators, whether physical, on smartphones, or online, makes finding the square root of 640 quick and accurate.
- Common mistakes to avoid include rounding errors, incorrect use of calculators, misinterpreting results, forgetting the ± sign, ignoring units, misunderstanding simplified radical forms, and skipping calculation steps.
- In physics and engineering, square roots are essential in various calculations, such as wave mechanics, electrical engineering, structural engineering, optics, and heat transfer.
- In everyday life, square roots are useful in cooking, gardening, real estate, travel, finance, and construction, demonstrating their practical significance.
By following proper calculation methods and understanding the importance of square roots, you can apply this mathematical concept effectively in both academic and practical scenarios. The example of the square root of 640 illustrates the usefulness and versatility of square roots in solving real-world problems.
In conclusion, mastering the calculation and application of square roots enhances your mathematical skills and enables you to tackle a wide range of problems efficiently and accurately. Whether for professional use in engineering or everyday tasks, knowing how to find and apply square roots is an invaluable tool.
Video này giải thích cách tính căn bậc hai của 640, cung cấp các ví dụ và ứng dụng thực tế.
Căn Bậc Hai của 640
READ MORE:
Video này giải thích cách tính căn bậc hai của 640, cung cấp các ví dụ và ứng dụng thực tế.
Căn Bậc Hai của 640