Topic what is 1/4 squared: Ever wondered what 1/4 squared is and how to calculate it? This article breaks down the concept of squaring fractions, offering a clear and easy-to-follow explanation. Learn the step-by-step process, avoid common mistakes, and explore practical applications to master this fundamental mathematical operation with confidence.
Table of Content
- Understanding the Square of 1/4
- Introduction to Squaring Fractions
- Basic Concept of Squaring
- Step-by-Step Process of Squaring 1/4
- Mathematical Representation
- Visual Explanation
- Common Mistakes and How to Avoid Them
- Practical Applications of Squaring Fractions
- Advanced Examples and Exercises
- Conclusion
- YOUTUBE: Tìm hiểu cách tính một phần tư bình phương: (1/4)^2 một cách chi tiết và dễ hiểu. Video này sẽ giúp bạn nắm vững khái niệm cơ bản và ứng dụng của phép toán này.
Understanding the Square of 1/4
Squaring a fraction involves multiplying the fraction by itself. Here, we will explain how to square 1/4 and provide its result in both fraction and decimal forms.
Calculation Steps
- Write the fraction: \( \frac{1}{4} \)
- Multiply the fraction by itself: \( \left( \frac{1}{4} \right) \times \left( \frac{1}{4} \right) \)
- Multiply the numerators: \( 1 \times 1 = 1 \)
- Multiply the denominators: \( 4 \times 4 = 16 \)
- The result is: \( \frac{1}{16} \)
Therefore, \( \left( \frac{1}{4} \right)^2 = \frac{1}{16} \).
Decimal Form
To convert the fraction \( \frac{1}{16} \) to a decimal:
- Divide the numerator by the denominator: \( 1 \div 16 = 0.0625 \)
Thus, \( \left( \frac{1}{4} \right)^2 = 0.0625 \) in decimal form.
Summary Table
| Expression | Result in Fraction Form | Result in Decimal Form |
|---|---|---|
| \( \left( \frac{1}{4} \right)^2 \) | \( \frac{1}{16} \) | 0.0625 |
In conclusion, squaring the fraction 1/4 yields 1/16 in fraction form and 0.0625 in decimal form. This simple mathematical operation can be useful in various applications, including algebra and geometry.
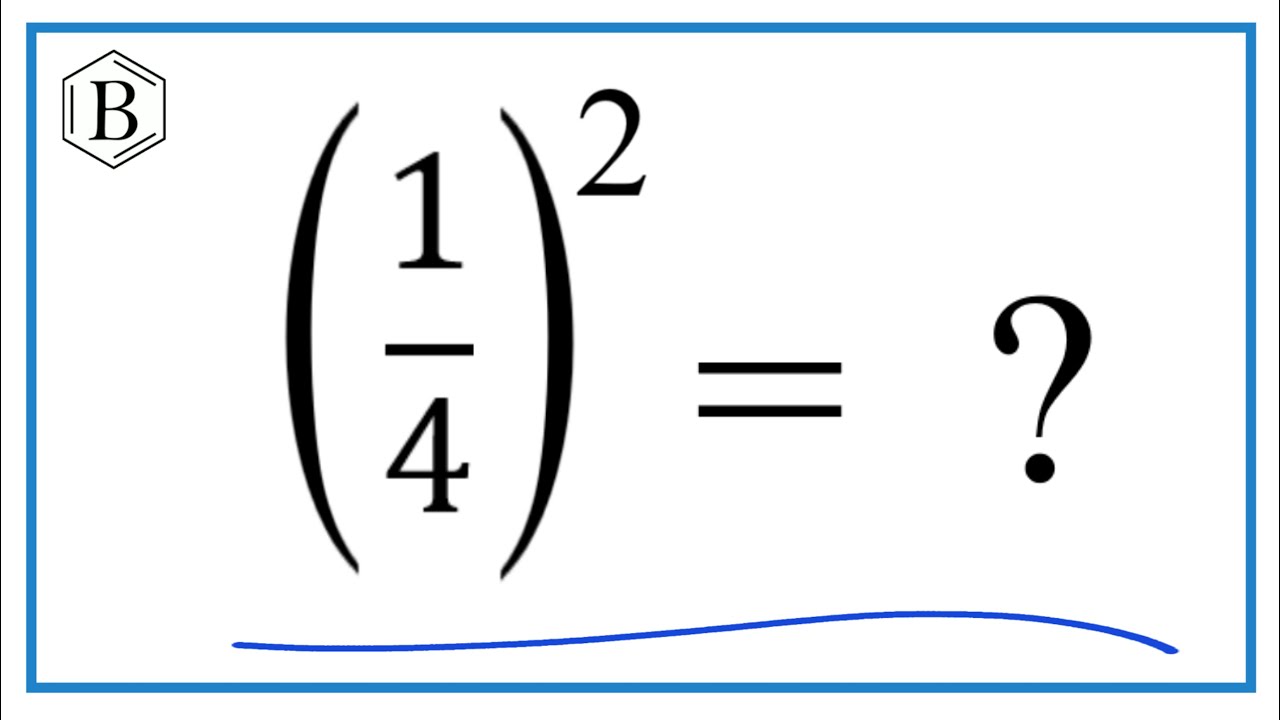
READ MORE:
Introduction to Squaring Fractions
Squaring a fraction is a straightforward process that involves multiplying the fraction by itself. This operation is essential in various mathematical contexts and can be applied to both simple and complex problems.
To understand squaring fractions, consider the fraction \( \frac{1}{4} \). When we square this fraction, we multiply it by itself:
\[
\left( \frac{1}{4} \right)^2 = \frac{1}{4} \times \frac{1}{4}
\]
Let's break this down step by step:
- Multiply the numerators together: \(1 \times 1 = 1\)
- Multiply the denominators together: \(4 \times 4 = 16\)
Thus, \( \left( \frac{1}{4} \right)^2 = \frac{1}{16} \).
Here is a summary in tabular form:
| Step | Operation | Result |
| 1 | Multiply numerators | 1 |
| 2 | Multiply denominators | 16 |
| Result | Combine results | \( \frac{1}{16} \) |
Squaring fractions is as simple as that. By understanding this fundamental operation, you can tackle more complex mathematical problems with confidence and ease.
Basic Concept of Squaring
Squaring a number means multiplying that number by itself. When we square a fraction, the process involves squaring both the numerator and the denominator.
For example, to square the fraction \( \frac{1}{4} \), we follow these steps:
- Square the numerator: \( 1^2 = 1 \)
- Square the denominator: \( 4^2 = 16 \)
- Combine the squared numerator and denominator to form the new fraction: \( \frac{1^2}{4^2} = \frac{1}{16} \)
This means \( \left( \frac{1}{4} \right)^2 = \frac{1}{16} \).
To summarize:
- Identify the fraction to be squared.
- Square the numerator of the fraction.
- Square the denominator of the fraction.
- Write the result as a new fraction with the squared numerator over the squared denominator.
Using Mathjax notation, the process can be represented as:
\[
\left( \frac{a}{b} \right)^2 = \frac{a^2}{b^2}
\]
For our specific example:
\[
\left( \frac{1}{4} \right)^2 = \frac{1^2}{4^2} = \frac{1}{16}
\]
Step-by-Step Process of Squaring 1/4
Squaring a fraction involves multiplying the fraction by itself. Here is a detailed, step-by-step process for squaring the fraction \( \frac{1}{4} \):
- Write down the fraction that needs to be squared:
\[
\frac{1}{4}
\] - Square the numerator (the top number of the fraction):
The numerator is 1. Squaring 1 means multiplying 1 by itself:
\[
1^2 = 1 \times 1 = 1
\] - Square the denominator (the bottom number of the fraction):
The denominator is 4. Squaring 4 means multiplying 4 by itself:
\[
4^2 = 4 \times 4 = 16
\] - Combine the squared numerator and denominator to form a new fraction:
After squaring both the numerator and the denominator, you place the squared numerator over the squared denominator:
\[
\frac{1^2}{4^2} = \frac{1}{16}
\] - Write the final result:
The result of squaring \( \frac{1}{4} \) is:
\[
\left( \frac{1}{4} \right)^2 = \frac{1}{16}
\]
Thus, squaring the fraction \( \frac{1}{4} \) results in \( \frac{1}{16} \).
Mathematical Representation
To understand the mathematical representation of squaring a fraction, let's break down the process using the example of squaring \( \frac{1}{4} \).
We start with the fraction:
\[
\frac{1}{4}
\]
When we square this fraction, we are multiplying the fraction by itself:
\[
\left( \frac{1}{4} \right) \times \left( \frac{1}{4} \right)
\]
This can be expressed using the exponent notation, where the fraction is raised to the power of 2:
\[
\left( \frac{1}{4} \right)^2
\]
To perform the squaring operation, we need to square both the numerator and the denominator separately:
- Square the numerator:
\[
1^2 = 1 \times 1 = 1
\] - Square the denominator:
\[
4^2 = 4 \times 4 = 16
\]
Combining these results, we get:
\[
\frac{1^2}{4^2} = \frac{1}{16}
\]
Therefore, the mathematical representation of squaring \( \frac{1}{4} \) is:
\[
\left( \frac{1}{4} \right)^2 = \frac{1}{16}
\]
This representation shows that squaring a fraction involves squaring both the numerator and the denominator separately and then combining them to form the final fraction.

Visual Explanation
To visually explain squaring the fraction \( \frac{1}{4} \), let's use a step-by-step approach with diagrams.
Step 1: Represent the fraction \( \frac{1}{4} \).
Imagine a square divided into 4 equal parts. One part out of these 4 represents the fraction \( \frac{1}{4} \).
\[
\begin{array}{|c|c|c|c|}
\hline
\color{blue}{1/4} & \frac{1}{4} & \frac{1}{4} & \frac{1}{4} \\
\hline
\end{array}
\]
Step 2: Square the fraction.
When we square \( \frac{1}{4} \), we are multiplying \( \frac{1}{4} \) by itself. This means we take one part out of 4 and divide it again into 4 parts.
\[
\begin{array}{|c|c|c|c|}
\hline
\color{blue}{1/4} & \frac{1}{4} & \frac{1}{4} & \frac{1}{4} \\
\hline
\end{array}
\Rightarrow
\begin{array}{|c|c|c|c|}
\hline
\color{blue}{\frac{1}{16}} & \frac{1}{16} & \frac{1}{16} & \frac{1}{16} \\
\hline
\frac{1}{16} & \frac{1}{16} & \frac{1}{16} & \frac{1}{16} \\
\hline
\frac{1}{16} & \frac{1}{16} & \frac{1}{16} & \frac{1}{16} \\
\hline
\frac{1}{16} & \frac{1}{16} & \frac{1}{16} & \frac{1}{16} \\
\hline
\end{array}
\]
Step 3: Observe the result.
Now, we see that the original \( \frac{1}{4} \) section, when squared, becomes \( \frac{1}{16} \). Each small square represents \( \frac{1}{16} \) of the whole.
Therefore, squaring \( \frac{1}{4} \) means dividing the already small section into even smaller parts, resulting in \( \frac{1}{16} \).
This visual approach helps to understand that squaring a fraction reduces its value because the area representing the fraction becomes smaller.
Common Mistakes and How to Avoid Them
When squaring fractions, it's important to follow the correct steps to avoid common mistakes. Here are some common errors and tips on how to avoid them:
- Mistake: Squaring the Denominator Only
Some people mistakenly only square the denominator, not the numerator.
Incorrect: \(\left( \frac{1}{4} \right)^2 = \frac{1}{4^2} = \frac{1}{16}\)
Correction: Ensure both the numerator and the denominator are squared.
Correct: \(\left( \frac{1}{4} \right)^2 = \frac{1^2}{4^2} = \frac{1}{16}\)
- Mistake: Forgetting to Square the Numerator
Another common mistake is to leave the numerator unchanged while squaring the denominator.
Incorrect: \(\left( \frac{1}{4} \right)^2 = \frac{1}{4} \times \frac{1}{4} = \frac{1}{4}\)
Correction: Remember to multiply the numerator by itself.
Correct: \(\left( \frac{1}{4} \right)^2 = \frac{1^2}{4^2} = \frac{1}{16}\)
- Mistake: Misinterpreting the Squaring Operation
Some might think squaring a fraction is the same as multiplying the fraction by 2.
Incorrect: \(\left( \frac{1}{4} \right)^2 = \frac{1}{4} \times 2 = \frac{2}{4} = \frac{1}{2}\)
Correction: Squaring means multiplying the fraction by itself, not by 2.
Correct: \(\left( \frac{1}{4} \right)^2 = \frac{1}{4} \times \frac{1}{4} = \frac{1}{16}\)
- Mistake: Simplifying Incorrectly After Squaring
Incorrect simplification after squaring can lead to wrong results.
Incorrect: \(\left( \frac{1}{4} \right)^2 = \frac{1}{16} = \frac{1}{4}\)
Correction: Simplify fractions properly before and after squaring if necessary.
Correct: \(\left( \frac{1}{4} \right)^2 = \frac{1}{16}\) (No further simplification needed as \(\frac{1}{16}\) is already in simplest form)
By being aware of these common mistakes and following the correct steps, you can accurately square fractions and avoid errors in your calculations.
Practical Applications of Squaring Fractions
Squaring fractions, such as \( \left(\frac{1}{4}\right)^2 \), is a fundamental mathematical concept with numerous practical applications in various fields. Understanding how to square fractions can be crucial in solving real-world problems. Here are some key applications:
- Geometry and Area Calculation: Squaring fractions is often used in geometry to calculate the area of squares and rectangles. For example, if the side length of a square is \(\frac{1}{4}\) units, the area of the square is \( \left(\frac{1}{4}\right)^2 = \frac{1}{16} \) square units.
- Physics and Engineering: In physics and engineering, squaring fractions can be essential when dealing with equations involving proportions and scaling. For instance, when calculating the moment of inertia or other properties that depend on squared terms.
- Probability and Statistics: Squaring fractions is used in probability and statistics, particularly in variance and standard deviation calculations. For example, the variance of a set of values involves squaring the differences from the mean, which can sometimes be fractions.
- Financial Calculations: In finance, squaring fractions can be useful when determining compound interest or returns over time. For example, the growth of an investment can involve squaring the rate of return, especially in risk assessment models.
- Scaling in Models: When creating scale models, such as architectural designs or miniature models, squaring fractions helps in accurately scaling dimensions. If a model is built at a scale of \(\frac{1}{4}\), the area or volume calculations will involve squaring this fraction to maintain accurate proportions.
Below is a table illustrating some examples of squaring fractions in practical scenarios:
| Scenario | Fraction | Square of the Fraction | Application |
|---|---|---|---|
| Side length of a square | \(\frac{1}{4}\) | \(\left(\frac{1}{4}\right)^2 = \frac{1}{16}\) | Calculating area |
| Scaling factor in a model | \(\frac{1}{2}\) | \(\left(\frac{1}{2}\right)^2 = \frac{1}{4}\) | Scaling dimensions |
| Probability of an event | \(\frac{1}{3}\) | \(\left(\frac{1}{3}\right)^2 = \frac{1}{9}\) | Variance calculation |
By understanding and applying the concept of squaring fractions, one can effectively solve a variety of practical problems across different domains.
Advanced Examples and Exercises
Now that we understand the basics of squaring fractions, let's explore some advanced examples and exercises to solidify our knowledge. We will work through several examples and provide detailed explanations for each step.
Example 1: Squaring a Fraction with Larger Numerators and Denominators
Consider the fraction \( \frac{3}{5} \). Let's square this fraction:
\[
\left( \frac{3}{5} \right)^2 = \frac{3^2}{5^2} = \frac{9}{25}
\]
Example 2: Squaring a Negative Fraction
Now, let's square the fraction \( -\frac{2}{7} \):
\[
\left( -\frac{2}{7} \right)^2 = \frac{(-2)^2}{7^2} = \frac{4}{49}
\]
Example 3: Squaring a Mixed Number
To square a mixed number, convert it to an improper fraction first. Let's square \( 1 \frac{1}{2} \):
Convert to improper fraction:
\[
1 \frac{1}{2} = \frac{3}{2}
\]
Square the fraction:
\[
\left( \frac{3}{2} \right)^2 = \frac{9}{4}
\]
Example 4: Squaring a Decimal
When squaring a decimal, convert it to a fraction first. Let's square \( 0.75 \):
Convert to fraction:
\[
0.75 = \frac{3}{4}
\]
Square the fraction:
\[
\left( \frac{3}{4} \right)^2 = \frac{9}{16}
\]
Exercises
- Square the fraction \( \frac{5}{8} \).
- Square the fraction \( -\frac{4}{9} \).
- Square the mixed number \( 2 \frac{2}{3} \).
- Square the decimal \( 0.6 \).
Solutions
| Exercise | Solution |
|---|---|
| \(\frac{5}{8}\) | \[ \left( \frac{5}{8} \right)^2 = \frac{25}{64} \] |
| \(-\frac{4}{9}\) | \[ \left( -\frac{4}{9} \right)^2 = \frac{16}{81} \] |
| \(2 \frac{2}{3}\) | Convert to improper fraction: \[ 2 \frac{2}{3} = \frac{8}{3} \] Square the fraction: \[ \left( \frac{8}{3} \right)^2 = \frac{64}{9} \] |
| \(0.6\) | Convert to fraction: \[ 0.6 = \frac{3}{5} \] Square the fraction: \[ \left( \frac{3}{5} \right)^2 = \frac{9}{25} \] |

Conclusion
Squaring fractions is a fundamental mathematical operation that has wide-ranging applications in various fields. Throughout this article, we've explored the process of squaring fractions in detail, using \( \frac{1}{4} \) as a primary example. Let's recap the key points:
- To square a fraction, multiply the fraction by itself. For \( \frac{1}{4} \), this means: \[ \left( \frac{1}{4} \right)^2 = \frac{1}{4} \times \frac{1}{4} = \frac{1 \times 1}{4 \times 4} = \frac{1}{16} \]
- The result can be expressed both in fraction form and decimal form. For \( \frac{1}{4} \):
- Fraction form: \( \frac{1}{16} \)
- Decimal form: \( 0.0625 \)
- This principle applies to any fraction, whether positive or negative, proper or improper.
Understanding how to square fractions is crucial for more advanced mathematical concepts such as algebra, calculus, and beyond. By mastering this skill, students can build a strong foundation for tackling complex problems with confidence.
Here are a few tips to avoid common mistakes:
- Always simplify fractions before and after squaring if possible.
- Remember that squaring a negative fraction results in a positive fraction.
- Double-check your multiplication of both the numerator and the denominator.
In conclusion, squaring fractions like \( \frac{1}{4} \) is a straightforward process that involves basic multiplication. By practicing with various examples and exercises, students can enhance their understanding and proficiency in this essential mathematical operation.
READ MORE:
Tìm hiểu cách tính một phần tư bình phương: (1/4)^2 một cách chi tiết và dễ hiểu. Video này sẽ giúp bạn nắm vững khái niệm cơ bản và ứng dụng của phép toán này.
Một phần tư bình phương: (1/4)^2