Topic how to add square roots and whole numbers: Adding square roots and whole numbers may seem complex, but with the right techniques, it becomes simple. This comprehensive guide will walk you through the basics, common mistakes to avoid, and practical examples to ensure you master this skill. Get ready to enhance your math proficiency with clear and easy steps!
Table of Content
- How to Add Square Roots and Whole Numbers
- Introduction to Adding Square Roots and Whole Numbers
- Understanding Square Roots
- Understanding Whole Numbers
- Basic Rules for Adding Square Roots and Whole Numbers
- Step-by-Step Guide to Adding Square Roots and Whole Numbers
- Common Mistakes to Avoid
- Examples of Adding Square Roots and Whole Numbers
- Advanced Techniques for Adding Square Roots
- Applications in Real Life
- YOUTUBE:
How to Add Square Roots and Whole Numbers
Adding square roots and whole numbers can seem challenging at first, but with the right approach, it becomes straightforward. Below are the steps and examples to help you understand how to add square roots and whole numbers.
Steps to Add Square Roots and Whole Numbers
- Identify the square root and the whole number you need to add.
- Understand that a square root is an irrational number, and a whole number is a rational number. They can be combined, but the result may not be simplified to a single term.
- Perform the addition by keeping the square root separate from the whole number.
Examples
Here are some examples to illustrate the process:
- Example 1: \( \sqrt{2} + 3 \)
Simply write the result as: \( \sqrt{2} + 3 \). This is the simplified form.
- Example 2: \( \sqrt{5} + 7 \)
Write the result as: \( \sqrt{5} + 7 \). There is no further simplification.
- Example 3: \( 4 + \sqrt{3} \)
Write the result as: \( 4 + \sqrt{3} \). This is already in its simplest form.
Practice Problems
Try solving the following problems on your own:
- \( \sqrt{7} + 2 \)
- \( 5 + \sqrt{11} \)
- \( \sqrt{13} + 6 \)
Conclusion
Adding square roots and whole numbers involves recognizing that they cannot be combined into a single term but can be written together in a simplified form. Practicing with various examples will help you become more comfortable with this type of addition.
READ MORE:
Introduction to Adding Square Roots and Whole Numbers
Adding square roots and whole numbers is an essential mathematical skill that combines basic arithmetic with an understanding of irrational numbers. This process involves handling square roots, which are values that, when multiplied by themselves, give the original number, and whole numbers, which are simple counting numbers without fractions or decimals.
To add square roots and whole numbers effectively, follow these steps:
- Understand the Components: Recognize the difference between a square root and a whole number. For example, in \( \sqrt{4} + 5 \), \( \sqrt{4} \) is the square root and 5 is the whole number.
- Separate Terms: Keep the square root and whole number terms separate as they cannot be directly combined into a simpler single term.
- Identify Simplifiable Square Roots: Check if the square root can be simplified to a whole number. For instance, \( \sqrt{4} = 2 \), so \( \sqrt{4} + 5 \) simplifies to \( 2 + 5 \).
- Add Simplified Terms: Add the simplified square root value to the whole number. Using the example above, \( 2 + 5 = 7 \).
- Express as Combined Terms: If the square root cannot be simplified to a whole number, write the expression with both terms. For instance, \( \sqrt{3} + 4 \) remains \( \sqrt{3} + 4 \).
By following these steps, you can confidently add square roots and whole numbers, ensuring accuracy and clarity in your calculations.
Understanding Square Roots
Square roots are fundamental in mathematics, representing a value that, when multiplied by itself, gives the original number. The square root of a number \( x \) is denoted as \( \sqrt{x} \). For example, \( \sqrt{9} = 3 \) because \( 3 \times 3 = 9 \).
Here are key points to understand square roots:
- Perfect Squares: Numbers like 1, 4, 9, 16, and 25 are perfect squares because their square roots are whole numbers (e.g., \( \sqrt{16} = 4 \)).
- Non-Perfect Squares: Numbers like 2, 3, 5, and 7 are not perfect squares, resulting in irrational numbers (e.g., \( \sqrt{2} \approx 1.414 \)).
- Properties of Square Roots:
- \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \)
- \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \)
- \( \sqrt{a^2} = a \) for non-negative \( a \)
- Simplifying Square Roots: To simplify square roots, factor the number under the root into its prime factors and pair them. For example, \( \sqrt{50} = \sqrt{25 \times 2} = 5\sqrt{2} \).
Let's look at some examples to solidify the understanding:
- Example 1: \( \sqrt{36} \)
The prime factors of 36 are \( 2 \times 2 \times 3 \times 3 \). Pairing the factors, we get \( 6 \times 6 = 36 \), so \( \sqrt{36} = 6 \).
- Example 2: \( \sqrt{45} \)
The prime factors of 45 are \( 3 \times 3 \times 5 \). Pairing the factors, we get \( 3\sqrt{5} \), so \( \sqrt{45} = 3\sqrt{5} \).
Understanding square roots is crucial for various mathematical operations, including adding square roots and whole numbers. This foundational knowledge helps in simplifying expressions and solving equations involving square roots.
Understanding Whole Numbers
Whole numbers are the set of numbers that include all positive integers and zero. They are fundamental in mathematics and are used for counting, ordering, and basic arithmetic operations. Whole numbers do not include fractions, decimals, or negative numbers.
Here are key points to understand whole numbers:
- Definition: Whole numbers are non-negative integers, including 0, 1, 2, 3, and so on.
- Properties of Whole Numbers:
- Closure: The sum or product of any two whole numbers is always a whole number. For example, \( 2 + 3 = 5 \) and \( 4 \times 5 = 20 \).
- Associativity: The way in which whole numbers are grouped in addition or multiplication does not change their sum or product. For example, \( (2 + 3) + 4 = 2 + (3 + 4) \) and \( (2 \times 3) \times 4 = 2 \times (3 \times 4) \).
- Commutativity: The order in which two whole numbers are added or multiplied does not change their sum or product. For example, \( 3 + 5 = 5 + 3 \) and \( 6 \times 2 = 2 \times 6 \).
- Identity: Adding 0 to a whole number does not change its value, and multiplying a whole number by 1 does not change its value. For example, \( 7 + 0 = 7 \) and \( 9 \times 1 = 9 \).
- Uses of Whole Numbers: Whole numbers are used in various everyday applications such as counting objects, measuring quantities, and labeling sequences.
Let's look at some examples to understand whole numbers better:
- Example 1: Counting objects
If you have 5 apples and you get 3 more, you count the total number of apples as \( 5 + 3 = 8 \).
- Example 2: Basic arithmetic
When you multiply 4 by 6, the product is a whole number: \( 4 \times 6 = 24 \).
Whole numbers form the basis of many mathematical concepts and operations. Understanding their properties and uses is essential for mastering more complex mathematical skills, such as adding square roots and whole numbers.
Basic Rules for Adding Square Roots and Whole Numbers
Adding square roots and whole numbers involves understanding the nature of each component and applying specific rules to ensure the calculation is done correctly. Here are the basic rules and steps to follow:
- Identify the Components:
Determine the square root and the whole number in the expression. For example, in \( \sqrt{5} + 3 \), \( \sqrt{5} \) is the square root and 3 is the whole number.
- Simplify the Square Root:
Check if the square root can be simplified to a whole number or a simpler square root. For instance, \( \sqrt{9} = 3 \) simplifies directly to a whole number.
- Keep Terms Separate:
If the square root cannot be simplified to a whole number, keep it as a separate term. For example, \( \sqrt{2} \) remains \( \sqrt{2} \).
- Combine Like Terms:
Add the whole number to any simplified square root term. If no simplification is possible, the expression remains a sum of the two terms. For example, \( \sqrt{2} + 3 \) remains \( \sqrt{2} + 3 \).
- Express the Result:
The final result should clearly show the separate terms. For example, \( \sqrt{5} + 3 \) is the final form if no further simplification is possible.
Here are some examples to illustrate these rules:
- Example 1: \( \sqrt{16} + 4 \)
\( \sqrt{16} = 4 \), so the expression simplifies to \( 4 + 4 = 8 \).
- Example 2: \( \sqrt{3} + 7 \)
The square root \( \sqrt{3} \) cannot be simplified further, so the expression remains \( \sqrt{3} + 7 \).
- Example 3: \( 2 + \sqrt{9} \)
\( \sqrt{9} = 3 \), so the expression simplifies to \( 2 + 3 = 5 \).
By following these basic rules, you can effectively add square roots and whole numbers, ensuring your calculations are accurate and your expressions are simplified correctly.

Step-by-Step Guide to Adding Square Roots and Whole Numbers
Adding square roots and whole numbers involves a systematic approach to ensure the calculations are done accurately. Follow this step-by-step guide to master this skill:
- Identify the Terms:
Determine which parts of the expression are square roots and which are whole numbers. For example, in \( \sqrt{7} + 5 \), \( \sqrt{7} \) is the square root and 5 is the whole number.
- Simplify the Square Root (if possible):
Check if the square root can be simplified to a whole number. For instance, \( \sqrt{25} = 5 \). If it can be simplified, perform the simplification.
- Combine Like Terms:
If the square root term has been simplified to a whole number, add it to the existing whole number. For example, \( \sqrt{25} + 4 \) simplifies to \( 5 + 4 = 9 \).
- Express the Terms Separately if Not Simplifiable:
If the square root cannot be simplified to a whole number, write the expression as a sum of the separate terms. For example, \( \sqrt{2} + 3 \) remains \( \sqrt{2} + 3 \).
- Final Expression:
The final expression should clearly show the combined or separate terms, depending on the simplification step. For example, \( \sqrt{18} + 2 \) simplifies to \( 3\sqrt{2} + 2 \).
Let's look at some examples to better understand this process:
- Example 1: \( \sqrt{49} + 6 \)
\( \sqrt{49} = 7 \), so the expression simplifies to \( 7 + 6 = 13 \).
- Example 2: \( \sqrt{5} + 3 \)
The square root \( \sqrt{5} \) cannot be simplified, so the expression remains \( \sqrt{5} + 3 \).
- Example 3: \( 4 + \sqrt{16} \)
\( \sqrt{16} = 4 \), so the expression simplifies to \( 4 + 4 = 8 \).
- Example 4: \( 2 + \sqrt{20} \)
\( \sqrt{20} \) can be simplified to \( 2\sqrt{5} \), so the expression becomes \( 2 + 2\sqrt{5} \).
By following these steps, you can confidently add square roots and whole numbers, ensuring your results are accurate and expressions are correctly simplified.
Common Mistakes to Avoid
When adding square roots and whole numbers, it is easy to make mistakes if you are not careful. Understanding common pitfalls can help you avoid errors and ensure your calculations are accurate. Here are some common mistakes to avoid:
- Incorrectly Simplifying Square Roots:
Make sure to simplify square roots correctly. For example, \( \sqrt{18} \) simplifies to \( 3\sqrt{2} \), not \( \sqrt{9 \times 2} \).
- Combining Unlike Terms:
Remember that you cannot combine a whole number and a square root into a single term. For instance, \( \sqrt{3} + 5 \) should not be written as \( \sqrt{8} \).
- Ignoring Simplification:
Always check if the square root can be simplified. For example, \( \sqrt{50} \) can be simplified to \( 5\sqrt{2} \). Not simplifying can make further calculations more complex.
- Arithmetic Errors:
Pay attention to basic arithmetic operations. Adding whole numbers incorrectly will affect your final result. For example, in \( \sqrt{4} + 7 \), \( \sqrt{4} = 2 \), so the correct answer is \( 2 + 7 = 9 \), not 8 or 10.
- Misinterpreting Radical Expressions:
Understand that \( \sqrt{a + b} \) is not equal to \( \sqrt{a} + \sqrt{b} \). For example, \( \sqrt{9 + 16} \neq \sqrt{9} + \sqrt{16} \). The correct calculation is \( \sqrt{25} = 5 \).
Here are some examples to illustrate these mistakes and how to avoid them:
- Example 1: \( \sqrt{12} + 4 \)
Incorrect: \( \sqrt{12} + 4 = \sqrt{16} = 4 \)
Correct: \( \sqrt{12} = 2\sqrt{3} \), so the expression is \( 2\sqrt{3} + 4 \). - Example 2: \( \sqrt{8} + 3 \)
Incorrect: \( \sqrt{8} + 3 = \sqrt{11} \)
Correct: \( \sqrt{8} = 2\sqrt{2} \), so the expression is \( 2\sqrt{2} + 3 \). - Example 3: \( 5 + \sqrt{25} \)
Incorrect: \( 5 + \sqrt{25} = 5 + 25 = 30 \)
Correct: \( \sqrt{25} = 5 \), so the expression simplifies to \( 5 + 5 = 10 \).
By being aware of these common mistakes and taking steps to avoid them, you can ensure that your calculations involving square roots and whole numbers are accurate and reliable.
Examples of Adding Square Roots and Whole Numbers
Adding square roots and whole numbers can be straightforward once you understand the principles involved. Here are some detailed examples to guide you through the process:
- Example 1: Simplified Square Root
Consider the expression \( \sqrt{25} + 4 \).
- Simplify the square root: \( \sqrt{25} = 5 \).
- Add the simplified square root to the whole number: \( 5 + 4 = 9 \).
So, \( \sqrt{25} + 4 = 9 \).
- Example 2: Non-Simplified Square Root
Consider the expression \( \sqrt{7} + 3 \).
- The square root \( \sqrt{7} \) cannot be simplified further.
- Combine the terms as they are: \( \sqrt{7} + 3 \).
So, \( \sqrt{7} + 3 \) remains \( \sqrt{7} + 3 \).
- Example 3: Simplification Required
Consider the expression \( \sqrt{50} + 2 \).
- Simplify the square root: \( \sqrt{50} = \sqrt{25 \times 2} = 5\sqrt{2} \).
- Add the whole number to the simplified square root: \( 5\sqrt{2} + 2 \).
So, \( \sqrt{50} + 2 = 5\sqrt{2} + 2 \).
- Example 4: Perfect Square Root
Consider the expression \( 3 + \sqrt{36} \).
- Simplify the square root: \( \sqrt{36} = 6 \).
- Add the whole number to the simplified square root: \( 3 + 6 = 9 \).
So, \( 3 + \sqrt{36} = 9 \).
- Example 5: Combining Terms
Consider the expression \( 1 + \sqrt{18} \).
- Simplify the square root: \( \sqrt{18} = \sqrt{9 \times 2} = 3\sqrt{2} \).
- Add the whole number to the simplified square root: \( 1 + 3\sqrt{2} \).
So, \( 1 + \sqrt{18} = 1 + 3\sqrt{2} \).
By following these examples, you can see how to approach different scenarios when adding square roots and whole numbers. Practice with various expressions to become more confident in performing these calculations accurately.
Advanced Techniques for Adding Square Roots
Adding square roots can become more complex when dealing with non-like terms or when simplification is required before addition. Here are some advanced techniques to help you add square roots effectively:
1. Simplifying Square Roots
Before adding square roots, simplify them whenever possible. Simplification involves finding the largest perfect square factor of the radicand (the number under the square root) and breaking it down:
- Example: Simplify \(\sqrt{50}\).
- Find the largest perfect square factor of 50, which is 25.
- Rewrite \(\sqrt{50}\) as \(\sqrt{25 \times 2}\).
- Simplify to \(5\sqrt{2}\).
2. Combining Like Terms
Square roots can only be added directly if they have the same radicand:
- Example: Add \(3\sqrt{2} + 4\sqrt{2}\).
- Since both terms have the same radicand (\(\sqrt{2}\)), add the coefficients: \(3 + 4 = 7\).
- Result: \(7\sqrt{2}\).
3. Adding Square Roots with Different Radicands
When square roots have different radicands, simplify each square root first and then see if they can be combined:
- Example: Add \(\sqrt{8} + \sqrt{18}\).
- Simplify each square root: \(\sqrt{8} = 2\sqrt{2}\) and \(\sqrt{18} = 3\sqrt{2}\).
- Combine the simplified terms: \(2\sqrt{2} + 3\sqrt{2} = 5\sqrt{2}\).
4. Adding Square Roots with Coefficients
When adding square roots with coefficients, simplify each term first, then multiply the coefficients and combine like terms:
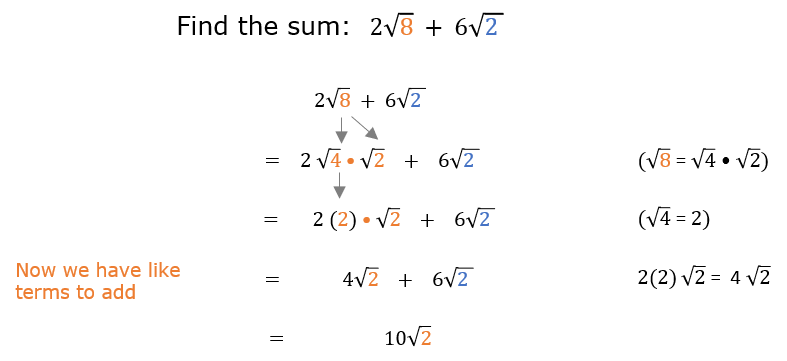
- Example: Add \(2\sqrt{8} + 5\sqrt{2}\).
- Simplify \(\sqrt{8}\) to \(2\sqrt{2}\), then rewrite the expression: \(2 \times 2\sqrt{2} = 4\sqrt{2}\).
- Combine the terms: \(4\sqrt{2} + 5\sqrt{2} = 9\sqrt{2}\).
5. Handling Complex Expressions
For more complex expressions, follow these steps:
- Simplify each square root individually.
- Group and combine like terms.
- Apply the distributive property if necessary.
Example: Simplify and add \(\sqrt{50} + 2\sqrt{32} + \sqrt{18}\).
- Simplify each term:
- \(\sqrt{50} = 5\sqrt{2}\)
- \(\sqrt{32} = 4\sqrt{2}\), so \(2\sqrt{32} = 2 \times 4\sqrt{2} = 8\sqrt{2}\)
- \(\sqrt{18} = 3\sqrt{2}\)
- Combine like terms: \(5\sqrt{2} + 8\sqrt{2} + 3\sqrt{2} = 16\sqrt{2}\).
Practice Problems
| Problem | Solution |
|---|---|
| \(\sqrt{72} + \sqrt{18}\) | Simplify each term: \(6\sqrt{2} + 3\sqrt{2} = 9\sqrt{2}\) |
| \(3\sqrt{50} + 2\sqrt{32}\) | Simplify each term: \(15\sqrt{2} + 8\sqrt{2} = 23\sqrt{2}\) |
| \(\sqrt{200} + \sqrt{8}\) | Simplify each term: \(10\sqrt{2} + 2\sqrt{2} = 12\sqrt{2}\) |
Applications in Real Life
Square roots and whole numbers play a significant role in various real-life applications across different fields. Here are some detailed examples to illustrate their practical use:
1. Architecture and Construction
Square roots are frequently used in architecture and construction to calculate dimensions and ensure structural integrity. For example, when designing a building, architects use the Pythagorean theorem to calculate the length of diagonals in rooms and other structural components.
- Calculating the diagonal of a rectangular room with sides of 6 meters and 8 meters: \[ \text{Diagonal} = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10 \text{ meters} \]
2. Finance
In finance, square roots are used to calculate the volatility of stocks, which helps investors assess the risk associated with an investment. Volatility is often derived from the standard deviation of the stock's returns, which involves taking the square root of the variance.
- For example, if the variance of a stock's returns is 16, the standard deviation (volatility) is: \[ \text{Volatility} = \sqrt{16} = 4 \]
3. Science and Engineering
Square roots are essential in various scientific calculations, such as determining the speed of an object under uniform acceleration or the intensity of sound waves.
- To calculate the velocity of an object after a certain time under uniform acceleration: \[ v = \sqrt{u^2 + 2as} \] where \(u\) is the initial velocity, \(a\) is the acceleration, and \(s\) is the displacement.
4. Statistics
In statistics, square roots are used to compute the standard deviation, a measure of data variability. The standard deviation is the square root of the variance.
- If the variance of a data set is 25, the standard deviation is: \[ \text{Standard Deviation} = \sqrt{25} = 5 \]
5. Geometry
Square roots are fundamental in geometry, particularly in the application of the Pythagorean theorem to find distances between points or the lengths of sides in right-angled triangles.
- Calculating the length of the hypotenuse in a right triangle with legs of 5 units and 12 units: \[ \text{Hypotenuse} = \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13 \text{ units} \]
6. Navigation
Pilots and sailors use square roots to calculate distances between waypoints using the Pythagorean theorem. This is crucial for accurate navigation and route planning.
- For instance, finding the distance between two points (3, 4) and (7, 1) on a map: \[ \text{Distance} = \sqrt{(7-3)^2 + (4-1)^2} = \sqrt{4^2 + 3^2} = \sqrt{16 + 9} = \sqrt{25} = 5 \text{ units} \]
7. Computer Graphics
In computer graphics, square roots are used to calculate distances and to normalize vectors, which are essential for rendering images and animations correctly.
- For example, normalizing a vector (3, 4) involves finding its magnitude: \[ \text{Magnitude} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]
8. Cryptography
Square roots are employed in cryptographic algorithms to secure data transmission. Algorithms like RSA use large prime numbers and their properties, including square roots, to encrypt and decrypt messages.
- Generating keys in RSA involves finding modular square roots, which is critical for creating secure encryption keys.
Cách Cộng & Trừ Số Radicals & Số Nguyên: Số Radicals