Adding Fractions with Square Roots: Master the Technique Easily

Adding fractions that contain square roots can be a bit more complex than adding regular fractions, but with some understanding and practice, it becomes manageable. Here is a detailed guide on how to add fractions with square roots.

Steps to Add Fractions with Square Roots

1. Identify the Fractions: Ensure that you clearly identify the fractions you need to add. For example, consider the fractions \(\frac{1}{\sqrt{2}}\) and \(\frac{1}{\sqrt{3}}\).
2. Rationalize the Denominators: To simplify the addition, rationalize the denominators. This means multiplying the numerator and the denominator by the conjugate of the denominator.
   • For \(\frac{1}{\sqrt{2}}\), multiply by \(\frac{\sqrt{2}}{\sqrt{2}}\): \[ \frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2} \]
   • For \(\frac{1}{\sqrt{3}}\), multiply by \(\frac{\sqrt{3}}{\sqrt{3}}\):

     
     \[
     \frac{1}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{\sqrt{3}}{3}

3. Find a Common Denominator: Identify the least common multiple (LCM) of the denominators to find a common denominator. For the fractions \(\frac{\sqrt{2}}{2}\) and \(\frac{\sqrt{3}}{3}\), the LCM of 2 and 3 is 6.
   • Convert each fraction to have the common denominator:

     
     \[
     \frac{\sqrt{2}}{2} \times \frac{3}{3} = \frac{3\sqrt{2}}{6}
     \]
     \[
     \frac{\sqrt{3}}{3} \times \frac{2}{2} = \frac{2\sqrt{3}}{6}

4. Add the Fractions: With the common denominator, add the numerators:

   
   \[
   \frac{3\sqrt{2}}{6} + \frac{2\sqrt{3}}{6} = \frac{3\sqrt{2} + 2\sqrt{3}}{6}
   \]

5. Simplify the Result (if possible): Check if the expression can be simplified further. In this case, \(\frac{3\sqrt{2} + 2\sqrt{3}}{6}\) is already in its simplest form.

Example Problems

Let's look at some additional examples to further illustrate the process:

• Example 1: \(\frac{1}{\sqrt{5}} + \frac{1}{\sqrt{7}}\)
  • Rationalize the denominators:

    
    \[
    \frac{1}{\sqrt{5}} \times \frac{\sqrt{5}}{\sqrt{5}} = \frac{\sqrt{5}}{5}
    \]
    \[
    \frac{1}{\sqrt{7}} \times \frac{\sqrt{7}}{\sqrt{7}} = \frac{\sqrt{7}}{7}

  • Find the common denominator (LCM of 5 and 7 is 35):

    
    \[
    \frac{\sqrt{5}}{5} \times \frac{7}{7} = \frac{7\sqrt{5}}{35}
    \]
    \[
    \frac{\sqrt{7}}{7} \times \frac{5}{5} = \frac{5\sqrt{7}}{35}

  • Add the fractions:

    
    \[
    \frac{7\sqrt{5}}{35} + \frac{5\sqrt{7}}{35} = \frac{7\sqrt{5} + 5\sqrt{7}}{35}

• Example 2: \(\frac{2}{\sqrt{6}} + \frac{3}{\sqrt{8}}\)
  • Rationalize the denominators:

    
    \[
    \frac{2}{\sqrt{6}} \times \frac{\sqrt{6}}{\sqrt{6}} = \frac{2\sqrt{6}}{6} = \frac{\sqrt{6}}{3}
    \]
    \[
    \frac{3}{\sqrt{8}} \times \frac{\sqrt{8}}{\sqrt{8}} = \frac{3\sqrt{8}}{8}
    \]
    \[
    \sqrt{8} = 2\sqrt{2} \implies \frac{3\sqrt{8}}{8} = \frac{3 \cdot 2\sqrt{2}}{8} = \frac{3\sqrt{2}}{4}

  • Find the common denominator (LCM of 3 and 4 is 12):

    
    \[
    \frac{\sqrt{6}}{3} \times \frac{4}{4} = \frac{4\sqrt{6}}{12}
    \]
    \[
    \frac{3\sqrt{2}}{4} \times \frac{3}{3} = \frac{9\sqrt{2}}{12}

  • Add the fractions:

    
    \[
    \frac{4\sqrt{6}}{12} + \frac{9\sqrt{2}}{12} = \frac{4\sqrt{6} + 9\sqrt{2}}{12}

By following these steps, you can effectively add fractions with square roots. Remember to rationalize the denominators, find a common denominator, and simplify the result if possible.

Adding fractions that include square roots can seem challenging at first, but with a clear understanding of the basic principles and steps involved, it becomes manageable. This section will guide you through the fundamental concepts and methods required to add fractions with square roots, ensuring you grasp the process thoroughly.

When dealing with fractions that have square roots, the key steps are similar to adding regular fractions but with additional considerations for the square roots in the numerators and denominators. Let's break down the process:

1. Understanding the Problem: Recognize that you are dealing with fractions that contain square roots. For example, consider adding \(\frac{1}{\sqrt{2}}\) and \(\frac{\sqrt{3}}{\sqrt{5}}\).
2. Rationalizing Denominators: To simplify the process, it's often helpful to rationalize the denominators. This means eliminating the square roots from the denominators by multiplying both the numerator and denominator by the conjugate of the denominator. For instance, to rationalize \(\frac{1}{\sqrt{2}}\), multiply by \(\frac{\sqrt{2}}{\sqrt{2}}\) to get \(\frac{\sqrt{2}}{2}\).
3. Finding a Common Denominator: Just like with regular fractions, you need a common denominator to add the fractions. This step may involve additional rationalization to ensure all fractions have a comparable base. For example, find the least common multiple (LCM) of the denominators.
4. Rewriting the Fractions: Once you have a common denominator, rewrite each fraction to reflect this denominator. This might involve multiplying both the numerator and denominator by the necessary factors to achieve the common denominator.
5. Adding the Fractions: With a common denominator in place, add the numerators together while keeping the denominator constant. Simplify the resulting fraction if possible.
6. Simplifying the Result: Finally, simplify the resulting fraction by combining like terms and reducing to the simplest form. Ensure the final answer is presented in the most reduced and rationalized form possible.

In the following sections, we will delve deeper into each of these steps, providing detailed explanations and examples to help you master the art of adding fractions with square roots.

Understanding how to work with fractions and square roots is essential for adding fractions that include these elements. Let's break down these concepts step-by-step:

Fractions

A fraction consists of a numerator (top part) and a denominator (bottom part). For example, in the fraction \(\frac{3}{4}\), 3 is the numerator, and 4 is the denominator.

Square Roots

The square root of a number is a value that, when multiplied by itself, gives the original number. The square root symbol is \(\sqrt{}\). For example:

• \(\sqrt{4} = 2\) because \(2 \times 2 = 4\)
• \(\sqrt{9} = 3\) because \(3 \times 3 = 9\)

Fractions with Square Roots

Fractions can include square roots in the numerator, the denominator, or both. Here are some examples:

• \(\frac{\sqrt{2}}{4}\)
• \(\frac{5}{\sqrt{3}}\)
• \(\frac{\sqrt{7}}{\sqrt{2}}\)

Simplifying Square Roots

Before adding fractions with square roots, it's often helpful to simplify the square roots. For instance:

\(\sqrt{18}\) can be simplified to \(\sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} = 3\sqrt{2}\).

Rationalizing the Denominator

If a fraction has a square root in the denominator, we can rationalize it by multiplying the numerator and the denominator by the square root. For example:

\(\frac{5}{\sqrt{3}}\) is rationalized as \(\frac{5}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{5\sqrt{3}}{3}\).

Combining Fractions

When adding fractions, finding a common denominator is crucial. This rule also applies when square roots are involved. For example:

To add \(\frac{1}{\sqrt{2}}\) and \(\frac{1}{\sqrt{3}}\), we first rationalize and then find a common denominator:

1. Rationalize: \(\frac{1 \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}} = \frac{\sqrt{2}}{2}\) and \(\frac{1 \cdot \sqrt{3}}{\sqrt{3} \cdot \sqrt{3}} = \frac{\sqrt{3}}{3}\).
2. Find a common denominator (6): \(\frac{3\sqrt{2}}{6} + \frac{2\sqrt{3}}{6} = \frac{3\sqrt{2} + 2\sqrt{3}}{6}\).

Practice and Application

With practice, handling fractions with square roots becomes more intuitive. Regularly simplifying square roots and rationalizing denominators will make these operations straightforward and less error-prone.

By mastering these steps, you'll be well-equipped to handle any problem involving fractions and square roots!

Adding fractions involves several key steps to ensure the fractions are combined correctly and simplified. Here are the basic steps to follow:

1. Identify the Denominators: Check if the fractions have the same denominator (the bottom number).
2. Find a Common Denominator:

   If the denominators are different, find a common denominator by determining the least common multiple (LCM) of the denominators. For example, for the fractions \(\frac{1}{3}\) and \(\frac{1}{4}\), the LCM of 3 and 4 is 12.

3. Convert to Equivalent Fractions:

   Convert each fraction to an equivalent fraction with the common denominator. Multiply both the numerator (top number) and the denominator by the necessary factor. For instance, to convert \(\frac{1}{3}\) to a fraction with a denominator of 12, multiply both the numerator and the denominator by 4 to get \(\frac{4}{12}\).

   Similarly, \(\frac{1}{4}\) can be converted to \(\frac{3}{12}\) by multiplying both the numerator and the denominator by 3.

4. Add the Numerators:

   Once the fractions have the same denominator, add the numerators while keeping the denominator the same. Using our example, \(\frac{4}{12} + \frac{3}{12} = \frac{7}{12}\).

5. Simplify the Fraction:

   Check if the resulting fraction can be simplified. A fraction is simplified when the greatest common divisor (GCD) of the numerator and the denominator is 1. For instance, \(\frac{7}{12}\) is already in its simplest form since 7 and 12 have no common factors other than 1.

Let's look at an example:

Consider adding \(\frac{2}{5}\) and \(\frac{3}{10}\).

1. The denominators are 5 and 10.
2. The LCM of 5 and 10 is 10.
3. Convert \(\frac{2}{5}\) to \(\frac{4}{10}\) (since \(2 \times 2 = 4\) and \(5 \times 2 = 10\)).
4. Now, the fractions are \(\frac{4}{10}\) and \(\frac{3}{10}\).
5. Add the numerators: \(4 + 3 = 7\), so \(\frac{4}{10} + \frac{3}{10} = \frac{7}{10}\).
6. \(\frac{7}{10}\) is already in its simplest form.

Following these steps ensures that you accurately add fractions and simplify them correctly.

Rationalizing the denominator involves removing the square root or other radicals from the denominator of a fraction. This process makes it easier to handle and simplifies further operations.

Here are the basic steps to rationalize denominators:

1. Identify the radical in the denominator. If the denominator is a single square root (monomial), multiply both the numerator and the denominator by that square root.

   For example, to rationalize \( \frac{4\sqrt{3}}{\sqrt{7}} \):

   
   Multiply both numerator and denominator by \( \sqrt{7} \):
   
   \( \frac{4\sqrt{3} \cdot \sqrt{7}}{\sqrt{7} \cdot \sqrt{7}} = \frac{4\sqrt{21}}{7} \).

2. If the denominator is a binomial involving a square root, multiply both the numerator and the denominator by the conjugate of the denominator. The conjugate is formed by changing the sign between the terms in the binomial.

   For example, to rationalize \( \frac{2}{3 + \sqrt{3}} \):

   
   Multiply both numerator and denominator by the conjugate \( 3 - \sqrt{3} \):
   
   \( \frac{2 \cdot (3 - \sqrt{3})}{(3 + \sqrt{3}) \cdot (3 - \sqrt{3})} = \frac{2(3 - \sqrt{3})}{3^2 - (\sqrt{3})^2} = \frac{2(3 - \sqrt{3})}{9 - 3} = \frac{2(3 - \sqrt{3})}{6} = \frac{6 - 2\sqrt{3}}{6} = 1 - \frac{\sqrt{3}}{3} \).

3. Simplify the resulting fraction if possible. Cancel any common factors between the numerator and the denominator.

Here are some more examples:

• Rationalize \( \frac{6 - \sqrt{5}}{\sqrt{8}} \):

  
  Multiply by \( \sqrt{8} \):
  
  \( \frac{(6 - \sqrt{5}) \cdot \sqrt{8}}{(\sqrt{8}) \cdot (\sqrt{8})} = \frac{6\sqrt{8} - \sqrt{40}}{8} = \frac{6 \cdot 2\sqrt{2} - 2\sqrt{10}}{8} = \frac{12\sqrt{2} - 2\sqrt{10}}{8} = \frac{6\sqrt{2} - \sqrt{10}}{4} \).

• Rationalize \( \frac{\sqrt{7}}{-3 - \sqrt{7}} \):

  
  Multiply by \( -3 + \sqrt{7} \):
  
  \( \frac{\sqrt{7} \cdot (-3 + \sqrt{7})}{(-3 - \sqrt{7}) \cdot (-3 + \sqrt{7})} = \frac{\sqrt{7} \cdot (-3 + \sqrt{7})}{9 - 7} = \frac{-3\sqrt{7} + 7}{2} \).

Rationalizing the denominator helps in simplifying expressions and solving equations more efficiently.

To add fractions, it's crucial to have a common denominator. This means that the denominators (the bottom numbers) of the fractions must be the same. Here are the steps to find common denominators:

1. Identify the Denominators:

   First, list the denominators of the fractions you want to add.

   • Example: For \( \frac{1}{4} \) and \( \frac{1}{6} \), the denominators are 4 and 6.
2. Find the Least Common Multiple (LCM):

   The least common multiple of the denominators is the smallest number that both denominators can divide into without a remainder.

   • Example: The LCM of 4 and 6 is 12, since 12 is the smallest number that both 4 and 6 divide into evenly.
3. Adjust the Fractions:

   Convert each fraction to an equivalent fraction with the common denominator found in step 2.

   • Multiply both the numerator and the denominator of each fraction by the necessary factor to reach the common denominator.
   • Example: For \( \frac{1}{4} \) to become a fraction with a denominator of 12, multiply both the numerator and the denominator by 3: \[ \frac{1}{4} \times \frac{3}{3} = \frac{3}{12} \]
   • For \( \frac{1}{6} \), multiply both the numerator and the denominator by 2: \[ \frac{1}{6} \times \frac{2}{2} = \frac{2}{12} \]
4. Rewrite the Fractions:

   Now both fractions have the same denominator and can be rewritten as follows:
   \[
   \frac{1}{4} = \frac{3}{12} \quad \text{and} \quad \frac{1}{6} = \frac{2}{12}
   \]

5. Add the Fractions:

   With common denominators, you can now add the numerators together while keeping the denominator the same:
   \[
   \frac{3}{12} + \frac{2}{12} = \frac{3 + 2}{12} = \frac{5}{12}
   \]

By following these steps, you can find common denominators and successfully add fractions. Practice this method to become proficient in handling fractions with different denominators.

Once you have rationalized the denominators and found a common denominator, you are ready to add the fractions. Follow these steps to successfully add fractions that include square roots:

1. Write the fractions with a common denominator: Ensure that both fractions have the same denominator. For example, if you have the fractions \(\frac{1}{\sqrt{2}}\) and \(\frac{1}{\sqrt{3}}\), you should rationalize them to get common denominators.

   After rationalizing and finding the common denominator, you might have something like \(\frac{\sqrt{3}}{3}\) and \(\frac{\sqrt{2}}{2}\).

2. Add the numerators: Keep the common denominator and add the numerators together.

   For example:

   
   \[
   \frac{\sqrt{3}}{3} + \frac{\sqrt{2}}{3} = \frac{\sqrt{3} + \sqrt{2}}{3}
   \]

   This simplifies the process and ensures the fractions are added correctly.

3. Simplify if necessary: Check if the resulting fraction can be simplified further. In many cases involving square roots, the expression might already be in its simplest form.

Let's look at a detailed example:

• Example:

• Add the fractions \(\frac{2}{\sqrt{5}}\) and \(\frac{3}{\sqrt{7}}\).

  1. Rationalize the denominators:

     
     \[
     \frac{2}{\sqrt{5}} \cdot \frac{\sqrt{5}}{\sqrt{5}} = \frac{2\sqrt{5}}{5}
     \]

     
     \[
     \frac{3}{\sqrt{7}} \cdot \frac{\sqrt{7}}{\sqrt{7}} = \frac{3\sqrt{7}}{7}
     \]

  2. Find the common denominator:

     The least common multiple (LCM) of 5 and 7 is 35. Adjust the fractions to have this common denominator:

     
     \[
     \frac{2\sqrt{5}}{5} \cdot \frac{7}{7} = \frac{14\sqrt{5}}{35}
     \]

     
     \[
     \frac{3\sqrt{7}}{7} \cdot \frac{5}{5} = \frac{15\sqrt{7}}{35}
     \]

  3. Add the fractions:

     
     \[
     \frac{14\sqrt{5}}{35} + \frac{15\sqrt{7}}{35} = \frac{14\sqrt{5} + 15\sqrt{7}}{35}
     \]

In this example, the final expression \(\frac{14\sqrt{5} + 15\sqrt{7}}{35}\) is the sum of the original fractions. This process ensures that fractions with square roots are added correctly and efficiently.

Once you have added fractions with square roots, the next step is to simplify the result. Simplifying can help to make the fraction more understandable and easier to work with. Here are the detailed steps for simplifying fractions with square roots:

1. Combine Like Terms:

   If your result has like terms involving square roots, combine them. For example, if your result is \(2\sqrt{3} + 3\sqrt{3}\), you can combine them to get \(5\sqrt{3}\).

2. Rationalize the Denominator:

   If your fraction has a square root in the denominator, rationalize it by multiplying the numerator and the denominator by the conjugate of the denominator. For example, to rationalize \(\frac{1}{\sqrt{2}}\), multiply by \(\frac{\sqrt{2}}{\sqrt{2}}\) to get \(\frac{\sqrt{2}}{2}\).

   Another example is rationalizing \(\frac{3}{2+\sqrt{5}}\):
   

   
   
   1. Multiply both the numerator and denominator by the conjugate of the denominator: \(2-\sqrt{5}\).
   
   
   2. This gives: \(\frac{3(2-\sqrt{5})}{(2+\sqrt{5})(2-\sqrt{5})}\).
   
   
   3. Simplify the denominator: \(4 - 5 = -1\).
   
   
   4. Thus, the fraction simplifies to: \(\frac{3(2-\sqrt{5})}{-1} = -3(2-\sqrt{5}) = -6 + 3\sqrt{5}\).
   
   
   
   


3. Simplify the Fraction:

   If both the numerator and the denominator have a common factor, divide by the greatest common factor to simplify. For example, \(\frac{4\sqrt{3}}{8}\) simplifies to \(\frac{\sqrt{3}}{2}\).

4. Combine and Simplify Radicals:

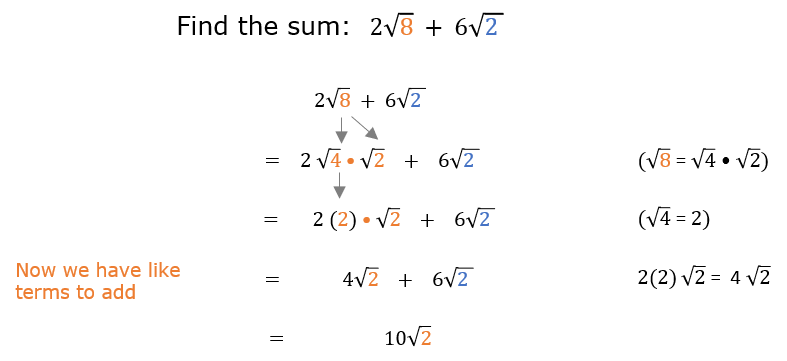
   If possible, simplify the square roots themselves. For example, \(\sqrt{12}\) can be simplified to \(2\sqrt{3}\) because \(12 = 4 \times 3\) and \(\sqrt{4} = 2\).

   Steps to simplify \(\sqrt{18}\):
   

   
   
   • Factor 18 into \(9 \times 2\).
   
   
   • Use the property \(\sqrt{ab} = \sqrt{a} \times \sqrt{b}\).
   
   
   • Simplify \(\sqrt{9} = 3\).
   
   
   • Thus, \(\sqrt{18} = 3\sqrt{2}\).
   
   
   
   


5. Express in Simplest Form:

   Ensure that the final result is in the simplest form. For example, \(\frac{4\sqrt{3}}{8\sqrt{2}}\) can be simplified as:
   

   
   
   1. Simplify the fraction: \(\frac{4}{8} = \frac{1}{2}\).
   
   
   2. Combine the radicals: \(\sqrt{3} / \sqrt{2} = \sqrt{3/2}\).
   
   
   3. Thus, \(\frac{4\sqrt{3}}{8\sqrt{2}} = \frac{\sqrt{3/2}}{2}\).
   
   
   
   

Following these steps will help you simplify your result effectively, making it easier to understand and use in further calculations.

Adding fractions that include square roots may seem challenging at first, but by following systematic steps, you can simplify and solve these problems effectively. Here are a few detailed examples:

Example 1: Simple Addition

Consider the fractions $\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}$.

1. First, find a common denominator. For $\sqrt{2}$ and $\sqrt{3}$, the common denominator is $\sqrt{6}$.
2. Convert each fraction to have this common denominator:
   • $\frac{1}{\sqrt{2}}=\frac{\sqrt{3}}{\sqrt{6}}$
   • $\frac{1}{\sqrt{3}}=\frac{\sqrt{2}}{\sqrt{6}}$
3. Add the fractions: $\frac{\sqrt{3}+\sqrt{2}}{\sqrt{6}}$

Example 2: Addition Requiring Rationalization

Consider the fractions $\frac{3}{\sqrt{5}}+\frac{2}{\sqrt{7}}$.

1. First, rationalize the denominators:
   • $\frac{3}{\sqrt{5}}=\frac{3\sqrt{5}}{5}$
   • $\frac{2}{\sqrt{7}}=\frac{2\sqrt{7}}{7}$
2. Find a common denominator. For 5 and 7, the common denominator is 35.
3. Convert each fraction to have this common denominator:
   • $\frac{3\sqrt{5}}{5}=\frac{21\sqrt{5}}{35}$
   • $\frac{2\sqrt{7}}{7}=\frac{10\sqrt{7}}{35}$
4. Add the fractions: $\frac{21\sqrt{5}+10\sqrt{7}}{35}$

Example 3: Complex Addition

Consider the fractions $\frac{2}{1+\sqrt{3}}+\frac{1}{2-\sqrt{3}}$.

1. Rationalize the denominators by multiplying by the conjugate:
   • $\frac{2}{1+\sqrt{3}}\backslash times\frac{1-\sqrt{3}}{1-\sqrt{3}}=\frac{21-\sqrt{3}}{-2}=\frac{-2}{-2}=1$
   • $\frac{1}{2-\sqrt{3}}\backslash times\frac{2+\sqrt{3}}{2+\sqrt{3}}=\frac{12+\sqrt{3}}{-1}=\frac{1}{-1}=-1$
2. Add the resulting fractions: $1+-1=0$

These examples illustrate the step-by-step process of adding fractions that contain square roots. Practice with these and similar problems to build your confidence and skills.

When adding fractions with square roots, several common mistakes can lead to incorrect results. Here are some key errors to watch out for and how to avoid them:

• Incorrectly Adding Denominators:

  One of the most common mistakes is to add the denominators directly. Remember, fractions can only be added if their denominators are the same. For example:

  \[
  \frac{3}{\sqrt{2}} + \frac{2}{\sqrt{3}} \neq \frac{3 + 2}{\sqrt{2} + \sqrt{3}}
  \]

  Instead, find a common denominator before adding:

  \[
  \frac{3\sqrt{3}}{\sqrt{2}\sqrt{3}} + \frac{2\sqrt{2}}{\sqrt{3}\sqrt{2}} = \frac{3\sqrt{3} + 2\sqrt{2}}{\sqrt{6}}
  \]

• Failing to Rationalize Denominators:

  Leaving square roots in the denominator is another frequent error. Always rationalize the denominator to simplify the fraction:

  \[
  \frac{1}{\sqrt{5}} = \frac{1}{\sqrt{5}} \cdot \frac{\sqrt{5}}{\sqrt{5}} = \frac{\sqrt{5}}{5}
  \]

• Improper Distribution of Square Roots:

  Ensure that square roots are correctly distributed across terms. For example, the square root of a sum is not the sum of the square roots:

  \[
  \sqrt{a + b} \neq \sqrt{a} + \sqrt{b}
  \]

• Incorrect Simplification:

  Simplifying fractions with square roots requires careful handling of terms. For instance:

  \[
  \frac{a + b}{c} \neq \frac{a}{c} + \frac{b}{c}
  \]

  Instead, simplify each term correctly while keeping the denominator consistent.

• Misapplying Square Root Properties:

  Remember that square root properties must be applied correctly. For example, multiplying inside and outside the square root incorrectly can lead to errors:

  \[
  \sqrt{ab} = \sqrt{a} \cdot \sqrt{b}
  \]

  Ensure to apply these properties correctly during calculations.

• Ignoring Negative Square Roots:

  When dealing with square roots, don't forget that both positive and negative roots should be considered, especially when solving equations:

  \[
  x^2 = 9 \quad \Rightarrow \quad x = \pm 3
  \]

When adding fractions with square roots, advanced techniques can greatly simplify the process and ensure accuracy. Here are some key methods to consider:

• Rationalizing Complex Denominators:

  When the denominator contains multiple terms including square roots, use the conjugate to rationalize the denominator. The conjugate is found by changing the sign between the terms.

  For example, to rationalize \( \frac{1}{\sqrt{3} + \sqrt{2}} \), multiply by the conjugate \( \frac{\sqrt{3} - \sqrt{2}}{\sqrt{3} - \sqrt{2}} \):

  
  \[
  \frac{1}{\sqrt{3} + \sqrt{2}} \times \frac{\sqrt{3} - \sqrt{2}}{\sqrt{3} - \sqrt{2}} = \frac{\sqrt{3} - \sqrt{2}}{(\sqrt{3})^2 - (\sqrt{2})^2} = \frac{\sqrt{3} - \sqrt{2}}{3 - 2} = \sqrt{3} - \sqrt{2}
  \]

• Using the Least Common Denominator (LCD):

  To add fractions with different square root denominators, find the LCD, which involves the product of the square roots. Adjust each fraction to have this common denominator.

  For example, to add \( \frac{1}{\sqrt{2}} \) and \( \frac{1}{\sqrt{3}} \), the LCD is \( \sqrt{2} \cdot \sqrt{3} = \sqrt{6} \). Adjust each fraction:

  
  \[
  \frac{1}{\sqrt{2}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{\sqrt{3}}{\sqrt{6}} \quad \text{and} \quad \frac{1}{\sqrt{3}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{\sqrt{6}}
  \]
  
  Now add the adjusted fractions:
  
  
  \[
  \frac{\sqrt{3}}{\sqrt{6}} + \frac{\sqrt{2}}{\sqrt{6}} = \frac{\sqrt{3} + \sqrt{2}}{\sqrt{6}}
  \]

• Combining and Simplifying Radicals:

  When dealing with more complex expressions, it’s often useful to simplify the radicals before performing any operations. Factor the radicands to find perfect squares.

  For instance, simplify \( \sqrt{50} \) and \( \sqrt{18} \) before adding:

  
  \[
  \sqrt{50} = \sqrt{25 \cdot 2} = 5\sqrt{2} \quad \text{and} \quad \sqrt{18} = \sqrt{9 \cdot 2} = 3\sqrt{2}
  \]
  
  Now, add \( 5\sqrt{2} \) and \( 3\sqrt{2} \):
  
  
  \[
  5\sqrt{2} + 3\sqrt{2} = 8\sqrt{2}
  \]

Here are some practice problems to help you master adding fractions with square roots. Follow each step carefully and simplify your answers as much as possible.

1. Add the following fractions:

   \(\frac{\sqrt{2}}{4} + \frac{3\sqrt{2}}{4}\)

   Solution:

   Since the denominators are the same, we can directly add the numerators:

   \(\frac{\sqrt{2} + 3\sqrt{2}}{4} = \frac{4\sqrt{2}}{4} = \sqrt{2}\)

2. Simplify and add the following fractions:

   \(\frac{5}{\sqrt{3}} + \frac{2}{\sqrt{3}}\)

   Solution:

   Combine the fractions:

   \(\frac{5 + 2}{\sqrt{3}} = \frac{7}{\sqrt{3}}\)

   Rationalize the denominator:

   \(\frac{7}{\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}} = \frac{7\sqrt{3}}{3}\)

3. Add the following fractions after rationalizing the denominators:

   \(\frac{2}{\sqrt{5}} + \frac{3}{\sqrt{7}}\)

   Solution:

   Rationalize the denominators:

   \(\frac{2}{\sqrt{5}} \cdot \frac{\sqrt{5}}{\sqrt{5}} = \frac{2\sqrt{5}}{5}\)

   \(\frac{3}{\sqrt{7}} \cdot \frac{\sqrt{7}}{\sqrt{7}} = \frac{3\sqrt{7}}{7}\)

   Since the denominators are different, find a common denominator:

   \(\frac{2\sqrt{5} \cdot 7 + 3\sqrt{7} \cdot 5}{35} = \frac{14\sqrt{5} + 15\sqrt{7}}{35}\)

4. Simplify and add the following fractions:

   \(\frac{\sqrt{6}}{2} + \frac{\sqrt{3}}{2}\)

   Solution:

   Since the denominators are the same, combine the numerators:

   \(\frac{\sqrt{6} + \sqrt{3}}{2}\)

   Since the square roots cannot be combined further, this is the simplest form.

5. Add the following fractions and simplify:

   \(\frac{4\sqrt{2}}{5} + \frac{3\sqrt{2}}{5}\)

   Solution:

   Combine the fractions since the denominators are the same:

   \(\frac{4\sqrt{2} + 3\sqrt{2}}{5} = \frac{7\sqrt{2}}{5}\)

These practice problems cover a range of scenarios involving adding fractions with square roots, including rationalizing denominators and finding common denominators. The more you practice, the more comfortable you will become with these types of problems.

Below are some frequently asked questions (FAQs) about adding fractions with square roots:

• Q1: Can you add fractions with different square roots in the denominators?

  A: Yes, but you need to find a common denominator first. This often involves rationalizing the denominators to eliminate the square roots.

• Q2: How do you rationalize the denominator of a fraction with a square root?

  A: To rationalize the denominator, multiply both the numerator and the denominator by the conjugate of the denominator if it is a binomial, or by the square root itself if it is a monomial. For example, to rationalize \(\frac{1}{\sqrt{2}}\), you multiply by \(\frac{\sqrt{2}}{\sqrt{2}}\) to get \(\frac{\sqrt{2}}{2}\).

• Q3: What steps are involved in adding fractions with square roots?
  1. Rationalize the denominators of the fractions if they contain square roots.
  2. Find a common denominator for the fractions.
  3. Rewrite each fraction with the common denominator.
  4. Add the numerators while keeping the common denominator.
  5. Simplify the resulting fraction if possible.
• Q4: Can you add fractions with square roots directly if their denominators are already rationalized and the same?

  A: Yes, if the denominators are the same and rationalized, you can directly add the numerators. For example, \(\frac{1}{2\sqrt{3}} + \frac{\sqrt{3}}{2\sqrt{3}} = \frac{1 + \sqrt{3}}{2\sqrt{3}}\).

• Q5: Are there any common mistakes to avoid when adding fractions with square roots?

  A: Yes, common mistakes include not rationalizing the denominators properly, failing to find a common denominator, and incorrectly simplifying the final result.

Adding fractions with square roots can be challenging, but by following systematic steps, it becomes manageable. The key steps involve rationalizing the denominators, finding common denominators, and carefully combining the fractions while simplifying the result. Mastery of these techniques not only improves your mathematical skills but also enhances your problem-solving abilities in various applications involving radicals.

To recap:

• Ensure the denominators are rationalized, removing any square roots.
• Find a common denominator for the fractions.
• Add the fractions, combining like terms and simplifying where possible.

By practicing these steps and understanding the underlying principles, you can confidently handle problems involving the addition of fractions with square roots. Always double-check your work for accuracy, and use these strategies to approach more complex problems with ease.

Remember, mathematics is a skill that improves with practice and persistence. Continue to practice, seek out challenging problems, and don't hesitate to revisit foundational concepts as needed. With dedication, you'll become proficient in adding fractions with square roots and ready to tackle even more advanced mathematical challenges.