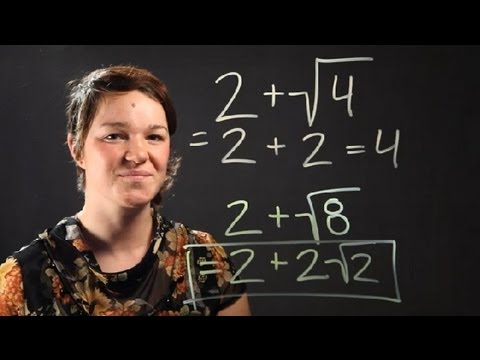Topic adding square roots calculator: The Adding Square Roots Calculator is a powerful tool that simplifies complex calculations, making math easier and more accessible. Whether you're a student, teacher, or enthusiast, this calculator helps you quickly and accurately add square roots, saving time and reducing errors. Discover the benefits of using this efficient and user-friendly calculator today!
Table of Content
- Adding Square Roots Calculator
- Introduction to Adding Square Roots
- How to Add Square Roots
- Examples of Adding Square Roots
- Step-by-Step Instructions
- Common Mistakes to Avoid
- Benefits of Using an Adding Square Roots Calculator
- Features of the Calculator
- Advanced Calculations
- Practical Applications
- Frequently Asked Questions (FAQs)
- Conclusion
- YOUTUBE:
Adding Square Roots Calculator
The "Adding Square Roots Calculator" is a useful tool designed to simplify the process of adding square roots. Whether you're a student, teacher, or math enthusiast, this calculator can help make complex calculations easier.
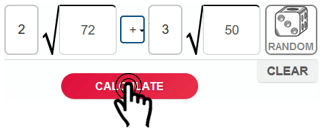
How to Use the Calculator
- Enter the values under the square roots you wish to add.
- Press the "Calculate" button.
- View the result displayed below.
Example Calculation
Let's say you want to add the square roots of 4 and 9.
\[ \sqrt{4} + \sqrt{9} \]
Using the calculator:
- Enter 4 and 9 into the respective input fields.
- The calculator computes \(\sqrt{4} = 2\) and \(\sqrt{9} = 3\).
- It then adds the results: \(2 + 3 = 5\).
The result is \(5\).
Advantages of Using the Calculator
- Speeds up calculations and reduces errors.
- Great for checking homework or verifying solutions.
- Helps in understanding the process of adding square roots.
Additional Features
The calculator also supports more complex inputs and can handle multiple square roots at once. For example:
\[ \sqrt{16} + \sqrt{25} + \sqrt{36} = 4 + 5 + 6 = 15 \]
Table of Common Square Roots
| Number | Square Root |
|---|---|
| 1 | \(\sqrt{1} = 1\) |
| 4 | \(\sqrt{4} = 2\) |
| 9 | \(\sqrt{9} = 3\) |
| 16 | \(\sqrt{16} = 4\) |
| 25 | \(\sqrt{25} = 5\) |
| 36 | \(\sqrt{36} = 6\) |

READ MORE:
Introduction to Adding Square Roots
Adding square roots is a fundamental mathematical operation often encountered in various fields of study and real-life applications. Understanding how to add square roots can simplify complex equations and enhance your problem-solving skills. This section provides a comprehensive introduction to the concept and process of adding square roots.
To add square roots, follow these steps:
- Simplify each square root as much as possible.
- Check if the square roots have the same radicand (the number inside the square root).
- If the radicands are the same, you can add the coefficients (the numbers in front of the square roots).
- If the radicands are different, you cannot combine the square roots directly, and the expression remains in its current form.
For example:
- \(\sqrt{4} + \sqrt{9}\): Simplify the square roots to get \(2 + 3\), which equals \(5\).
- \(\sqrt{18} + \sqrt{8}\): Simplify the square roots to get \(\sqrt{9 \times 2} + \sqrt{4 \times 2} = 3\sqrt{2} + 2\sqrt{2}\). Since the radicands are the same, you can add the coefficients to get \((3+2)\sqrt{2} = 5\sqrt{2}\).
In cases where the radicands are different, such as \(\sqrt{3} + \sqrt{5}\), the expression cannot be simplified further and remains as it is.
Using an adding square roots calculator can greatly simplify these calculations, allowing you to focus on understanding the concepts rather than getting bogged down by arithmetic.
How to Add Square Roots
Adding square roots can be straightforward if you follow a few simple steps. This section will guide you through the process of adding square roots step by step, ensuring you understand the method thoroughly.
To add square roots, follow these steps:
- Simplify Each Square Root: Break down each square root into its simplest form. For example:
- \(\sqrt{8} = \sqrt{4 \times 2} = 2\sqrt{2}\)
- \(\sqrt{18} = \sqrt{9 \times 2} = 3\sqrt{2}\)
- Check for Common Radicands: Ensure the radicands (the numbers inside the square roots) are the same. If they are, you can combine the square roots by adding the coefficients.
- For example: \(2\sqrt{2} + 3\sqrt{2} = (2+3)\sqrt{2} = 5\sqrt{2}\)
- Add the Coefficients: If the radicands are the same, add the coefficients in front of the square roots.
- \(a\sqrt{b} + c\sqrt{b} = (a+c)\sqrt{b}\)
- Leave Different Radicands As Is: If the radicands are different, you cannot combine the square roots directly. For example:
- \(\sqrt{2} + \sqrt{3}\) remains \(\sqrt{2} + \sqrt{3}\)
Let's look at a more complex example:
- \(\sqrt{50} + \sqrt{18}\)
- Simplify: \(\sqrt{50} = \sqrt{25 \times 2} = 5\sqrt{2}\)
- Simplify: \(\sqrt{18} = \sqrt{9 \times 2} = 3\sqrt{2}\)
- Since the radicands are the same (\(\sqrt{2}\)), add the coefficients: \(5\sqrt{2} + 3\sqrt{2} = (5+3)\sqrt{2} = 8\sqrt{2}\)
In cases where simplification is not possible, the expressions are left in their current form. For instance, \(\sqrt{7} + \sqrt{11}\) cannot be simplified further and remains as is.
Using an adding square roots calculator can help you perform these operations quickly and accurately, ensuring you get the correct results every time.
Examples of Adding Square Roots
Adding square roots can be made clearer through various examples. This section provides step-by-step examples to demonstrate the process of adding square roots effectively.
Example 1: Simplified Square Roots
- Consider the square roots \(\sqrt{4}\) and \(\sqrt{9}\).
- Simplify each square root:
- \(\sqrt{4} = 2\)
- \(\sqrt{9} = 3\)
- Add the simplified values:
- \(2 + 3 = 5\)
Example 2: Adding Like Radicands
- Consider the square roots \(2\sqrt{5}\) and \(3\sqrt{5}\).
- Since the radicands are the same (\(\sqrt{5}\)), you can add the coefficients:
- \(2\sqrt{5} + 3\sqrt{5} = (2+3)\sqrt{5} = 5\sqrt{5}\)
Example 3: Different Radicands
- Consider the square roots \(\sqrt{2}\) and \(\sqrt{3}\).
- Since the radicands are different, the expression remains as is:
- \(\sqrt{2} + \sqrt{3}\)
Example 4: Simplifying Before Adding
- Consider the square roots \(\sqrt{50}\) and \(\sqrt{18}\).
- Simplify each square root:
- \(\sqrt{50} = \sqrt{25 \times 2} = 5\sqrt{2}\)
- \(\sqrt{18} = \sqrt{9 \times 2} = 3\sqrt{2}\)
- Since the radicands are the same (\(\sqrt{2}\)), add the coefficients:
- \(5\sqrt{2} + 3\sqrt{2} = (5+3)\sqrt{2} = 8\sqrt{2}\)
Example 5: Complex Addition
- Consider the square roots \(\sqrt{32} + \sqrt{72}\).
- Simplify each square root:
- \(\sqrt{32} = \sqrt{16 \times 2} = 4\sqrt{2}\)
- \(\sqrt{72} = \sqrt{36 \times 2} = 6\sqrt{2}\)
- Since the radicands are the same (\(\sqrt{2}\)), add the coefficients:
- \(4\sqrt{2} + 6\sqrt{2} = (4+6)\sqrt{2} = 10\sqrt{2}\)
These examples illustrate different scenarios of adding square roots, showing when simplification is possible and when expressions must remain as they are. Utilizing an adding square roots calculator can streamline this process, making it quicker and more accurate.
Step-by-Step Instructions
Adding square roots can be done easily by following these step-by-step instructions. This guide will help you understand the process in detail, ensuring accurate and efficient calculations.
- Identify the Square Roots:
Determine the square roots you need to add. For example, let's consider \(\sqrt{18}\) and \(\sqrt{8}\).
- Simplify Each Square Root:
Break down each square root into its simplest form.
- \(\sqrt{18} = \sqrt{9 \times 2} = 3\sqrt{2}\)
- \(\sqrt{8} = \sqrt{4 \times 2} = 2\sqrt{2}\)
- Check for Common Radicands:
Ensure the radicands (the numbers inside the square roots) are the same.
- In this example, both simplified square roots have the same radicand \(\sqrt{2}\).
- Add the Coefficients:
If the radicands are the same, add the coefficients in front of the square roots.
- For \(\sqrt{18}\) and \(\sqrt{8}\), we get: \(3\sqrt{2} + 2\sqrt{2} = (3+2)\sqrt{2} = 5\sqrt{2}\)
- Handle Different Radicands:
If the radicands are different, the square roots cannot be added directly.
- For example, \(\sqrt{2} + \sqrt{3}\) remains \(\sqrt{2} + \sqrt{3}\).
- Verify Your Results:
Double-check your calculations to ensure accuracy. Using an adding square roots calculator can help verify the results quickly.
Let's look at another example to reinforce the process:
Example: Add \(\sqrt{50}\) and \(\sqrt{18}\).
- Simplify each square root:
- \(\sqrt{50} = \sqrt{25 \times 2} = 5\sqrt{2}\)
- \(\sqrt{18} = \sqrt{9 \times 2} = 3\sqrt{2}\)
- Since both simplified square roots have the same radicand \(\sqrt{2}\), add the coefficients:
- \(5\sqrt{2} + 3\sqrt{2} = (5+3)\sqrt{2} = 8\sqrt{2}\)
By following these step-by-step instructions, you can confidently add square roots, simplifying and combining them as needed. Utilizing an adding square roots calculator can further streamline the process, ensuring accuracy and efficiency in your calculations.
Common Mistakes to Avoid
When adding square roots, several common mistakes can lead to incorrect results. Understanding these pitfalls can help improve your accuracy and confidence when performing these calculations. Here are the most frequent mistakes to watch out for:
-
Adding Unlike Square Roots:
A common error is trying to directly add square roots with different radicands (the numbers under the square root symbol). Only square roots with the same radicand can be added together. For example:
\[
\sqrt{2} + \sqrt{3} \neq \sqrt{5}
\]Instead, the correct expression remains:
\[
\sqrt{2} + \sqrt{3}
\] -
Failing to Simplify First:
Before adding square roots, always simplify them to their lowest terms. Simplification can often reveal like terms that can be added. For example:
\[
\sqrt{18} + \sqrt{8} \quad \text{simplifies to} \quad 3\sqrt{2} + 2\sqrt{2} = 5\sqrt{2}
\] -
Incorrectly Applying Arithmetic Rules:
A common misconception is to assume that the sum of square roots can be combined into a single square root. This is incorrect. For instance:
\[
\sqrt{a} + \sqrt{b} \neq \sqrt{a + b}
\]Each square root should be treated individually.
-
Misinterpreting Square Root Signs:
Confusing the square root sign with other mathematical symbols or operations can lead to errors. Ensure clarity in what each symbol represents and the correct application of operations involving square roots.
-
Overlooking Negative Roots:
Remember that every positive number has both a positive and a negative square root. Failing to consider the negative root can result in incomplete solutions. For example:
\[
\sqrt{x^2} = \pm x
\]
By being aware of these common mistakes, you can enhance your understanding and execution when adding square roots, leading to more accurate and reliable results.
Benefits of Using an Adding Square Roots Calculator
Using an adding square roots calculator can significantly enhance your mathematical workflow and accuracy. Here are some key benefits of utilizing this tool:
-
Accuracy and Precision:
Calculators designed for adding square roots eliminate the risk of human error, ensuring that your results are precise. This is especially crucial when dealing with complex calculations where manual arithmetic could lead to mistakes.
For instance, adding simplified square roots like \(\sqrt{18} + \sqrt{50}\) involves steps that are easily mishandled manually. The calculator simplifies these steps accurately:
\[
\sqrt{18} + \sqrt{50} = 3\sqrt{2} + 5\sqrt{2} = 8\sqrt{2}
\] -
Time Efficiency:
Using a calculator speeds up the process of adding square roots, which can be particularly beneficial when dealing with multiple or large datasets. This efficiency allows you to focus on interpreting results rather than performing repetitive calculations.
-
Simplification and Clarification:
A good calculator simplifies square roots to their lowest terms before adding them, providing a clear and simplified result. This can help in understanding the relationships between different terms in your calculations.
For example, adding \(\sqrt{72} + \sqrt{128}\) manually requires simplification:
\[
\sqrt{72} = 6\sqrt{2} \quad \text{and} \quad \sqrt{128} = 8\sqrt{2}
\]
The calculator directly provides the result:
\[
6\sqrt{2} + 8\sqrt{2} = 14\sqrt{2}
\] -
Learning and Educational Aid:
Many square root calculators offer step-by-step solutions that help users understand the process of adding square roots. This feature is particularly useful for students learning about square roots and their properties, as it reinforces concepts and techniques.
-
Handling Complex Expressions:
Adding square roots can become cumbersome when dealing with complex expressions or when multiple roots are involved. A calculator efficiently handles these cases, providing quick solutions and reducing cognitive load.
-
Visualization and Graphing:
Advanced calculators often include graphing capabilities, allowing users to visualize the results of adding square roots. This can be beneficial in understanding how square root functions behave and interact graphically.
Overall, using an adding square roots calculator offers numerous benefits, from improving accuracy and efficiency to enhancing educational understanding and handling complex calculations with ease.
Features of the Calculator
An adding square roots calculator comes equipped with a range of features designed to simplify and enhance your mathematical calculations. Here’s a detailed look at the key functionalities these calculators typically offer:
-
Basic Arithmetic with Square Roots:
At its core, the calculator can handle the addition of square roots with ease. Whether you are adding two simple roots or multiple complex roots, the calculator ensures accurate and quick results.
For example:
\[
\sqrt{5} + \sqrt{20} = \sqrt{5} + 2\sqrt{5} = 3\sqrt{5}
\] -
Simplification of Square Roots:
The calculator automatically simplifies square roots to their lowest terms before performing any operations. This feature is crucial for obtaining the most concise and accurate form of the result.
For instance:
\[
\sqrt{45} + \sqrt{75} \text{ simplifies to } 3\sqrt{5} + 5\sqrt{3}
\] -
Handling Complex Expressions:
These calculators are capable of managing and simplifying complex expressions involving multiple square roots and other mathematical operations. This is particularly useful in advanced mathematics and engineering tasks.
Example:
\[
\sqrt{32} + \sqrt{50} + \frac{\sqrt{18}}{2} \text{ simplifies to } 4\sqrt{2} + 5\sqrt{2} + \frac{3\sqrt{2}}{2}
\] -
Step-by-Step Solutions:
Many calculators provide detailed, step-by-step explanations of how they arrived at the result. This feature is invaluable for educational purposes, helping users understand the underlying processes and principles.
Example:
\[
\sqrt{27} + \sqrt{48} \rightarrow 3\sqrt{3} + 4\sqrt{3} \rightarrow 7\sqrt{3}
\] -
Graphical Representation:
Advanced calculators include graphing capabilities that allow users to visualize the addition of square roots. This can be particularly helpful in understanding the behavior of functions involving square roots.
For example, plotting the functions \( y = \sqrt{x} + \sqrt{x-1} \) can provide insights into how these expressions behave over a range of values.
-
Support for Symbolic Computation:
Beyond numerical calculations, some calculators can perform symbolic math, allowing for the manipulation and simplification of expressions in their algebraic form. This feature is essential for advanced mathematics and theoretical work.
Example:
\[
\sqrt{a} + \sqrt{b} \text{ remains in symbolic form for general algebraic manipulation.}
\] -
Integration with Other Math Functions:
These calculators are often integrated with other mathematical functions, enabling seamless transitions between operations. You can combine square root additions with other operations like multiplication, division, and exponentiation.
For instance:
\[
2(\sqrt{7} + \sqrt{3})^2
\]
These features make adding square roots calculators versatile and powerful tools, suitable for a wide range of mathematical applications from basic arithmetic to advanced algebraic manipulations.
Advanced Calculations
When it comes to advanced calculations involving square roots, a specialized calculator can handle a variety of complex operations with ease. Here’s a closer look at some of the sophisticated functionalities these calculators offer:
-
Combining Multiple Square Roots:
Advanced calculators can efficiently add multiple square roots, even if they initially seem dissimilar. The calculator simplifies each root to its lowest terms and then combines them. This is particularly useful for solving problems involving several terms.
For example:
\[
\sqrt{18} + \sqrt{50} + \sqrt{72} = 3\sqrt{2} + 5\sqrt{2} + 6\sqrt{2} = 14\sqrt{2}
\] -
Manipulating Nested Square Roots:
Some problems involve nested square roots, which can be challenging to simplify manually. Advanced calculators can resolve these into simpler forms.
Example:
\[
\sqrt{2 + \sqrt{3}} + \sqrt{5 - \sqrt{2}}
\] -
Handling Higher-Order Roots and Radical Expressions:
In addition to square roots, these calculators can manage other types of roots (e.g., cube roots, fourth roots) and combine them with square roots in the same expression. They can simplify expressions like:
\[
\sqrt[3]{27} + \sqrt{25} = 3 + 5 = 8
\]
or:
\[
\sqrt{2} \times \sqrt[4]{16} = \sqrt{2} \times 2 = 2\sqrt{2}
\] -
Solving Equations Involving Square Roots:
Advanced calculators can solve equations that include square roots. They isolate the square root term and solve for the variable, providing both the positive and negative solutions where applicable.
For instance, solving:
\[
x + \sqrt{x - 1} = 5
\] -
Integration with Algebraic Operations:
These calculators allow you to perform algebraic operations on expressions involving square roots. You can add, subtract, multiply, and divide these expressions seamlessly.
Example:
\[
\left( \sqrt{3} + \sqrt{5} \right) \times \left( \sqrt{2} - \sqrt{7} \right)
\] -
Support for Complex Numbers:
Many advanced calculators can handle operations involving complex numbers, including those with square roots. This includes simplifying expressions and performing arithmetic with complex roots.
For example:
\[
\sqrt{-4} = 2i \quad \text{and} \quad \sqrt{2 + 3i}
\] -
Graphing and Visualization:
Advanced calculators often include graphing functionalities that can visualize the behavior of functions involving square roots. This helps in understanding how changes in the input affect the function.
For example, graphing \( y = \sqrt{x^2 + 1} \) can illustrate how the function behaves across different values of \( x \).
These capabilities make advanced adding square roots calculators invaluable tools for tackling complex mathematical problems efficiently and accurately.

Practical Applications
Adding square roots is a fundamental mathematical operation that has various practical applications across different fields. Understanding how to add square roots can be useful in the following scenarios:
- Engineering and Architecture: Engineers and architects often use square roots in their calculations when designing structures. For instance, calculating the diagonal length of a rectangular component involves the square root operation, and combining these lengths may require adding square roots.
- Physics: In physics, square roots are used to determine values such as distances, velocities, and other measurements derived from equations involving squaring. Adding these values accurately is crucial in experiments and practical applications.
- Computer Science: In algorithms and computer graphics, square roots are used in various calculations such as determining distances between points. Efficiently adding these square roots can optimize computational tasks.
- Finance: In finance, square roots are involved in statistical calculations and risk assessment models. For example, the standard deviation, a measure of risk, is often added to other square root calculations for comprehensive analysis.
- Education: Teachers and students use the concept of adding square roots in problem-solving exercises and standardized tests. Mastering this skill enhances mathematical understanding and competence.
Below are some step-by-step examples of practical applications where adding square roots is necessary:
- Finding the Hypotenuse in Geometry:
Given two sides of a right triangle, you can find the hypotenuse (c) using the Pythagorean theorem: \(c = \sqrt{a^2 + b^2}\). If you have multiple triangles, you may need to add these hypotenuse values.
Example: If triangle 1 has sides 3 and 4, and triangle 2 has sides 5 and 12:
- Hypotenuse of triangle 1: \(c_1 = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5\)
- Hypotenuse of triangle 2: \(c_2 = \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13\)
- Total hypotenuse value: \(c_1 + c_2 = 5 + 13 = 18\)
- Combining Standard Deviations:
In statistics, when combining datasets, you might need to add the standard deviations which involve square roots.
Example: If two datasets have standard deviations of \( \sigma_1 = \sqrt{4} \) and \( \sigma_2 = \sqrt{9} \):
- Standard deviation of dataset 1: \( \sigma_1 = 2 \)
- Standard deviation of dataset 2: \( \sigma_2 = 3 \)
- Combined standard deviation (simplified): \( \sigma_{\text{total}} = \sqrt{\sigma_1^2 + \sigma_2^2} = \sqrt{2^2 + 3^2} = \sqrt{4 + 9} = \sqrt{13} \approx 3.6 \)
These examples demonstrate the necessity and practicality of adding square roots in various real-world scenarios, enhancing the accuracy and efficiency of calculations.
Frequently Asked Questions (FAQs)
-
What is an adding square roots calculator?
An adding square roots calculator is an online tool designed to help you quickly and accurately add two or more square root values. It simplifies the process by providing the result and showing the step-by-step calculations.
-
How do I use an adding square roots calculator?
To use the calculator, enter the square root values you wish to add into the designated input fields. The calculator will automatically compute the sum of the square roots and display the result.
-
Can I add square roots with different radicands?
Square roots can only be directly added if they have the same radicand. If the radicands are different, you must first simplify the square roots and check if they can be expressed with a common radicand.
-
What are like terms in square root addition?
Like terms in square root addition are square roots that have the same radicand. For example, \( \sqrt{2} \) and \( 3\sqrt{2} \) are like terms and can be combined, but \( \sqrt{2} \) and \( \sqrt{3} \) are not.
-
How do I simplify square roots before adding?
To simplify a square root, factor the number under the root into its prime factors and simplify by taking out pairs of factors. For example, \( \sqrt{50} \) can be simplified to \( 5\sqrt{2} \).
-
What if the square roots have coefficients?
If the square roots have coefficients, you should first simplify the square root terms and then multiply the coefficients by the simplified square root. Combine the like terms to get the final result.
-
Can the calculator handle complex square root expressions?
Yes, advanced square root calculators can handle complex expressions, including those with multiple terms and coefficients. They provide detailed step-by-step solutions.
-
What are the benefits of using an adding square roots calculator?
Using an adding square roots calculator saves time, reduces errors, and helps in understanding the steps involved in the addition process. It is particularly useful for students and professionals who need quick and accurate results.
-
Are there any practical applications for adding square roots?
Adding square roots is useful in various fields such as engineering, physics, and computer science, where complex calculations involving square roots are common. It is also used in solving mathematical problems and equations.
Conclusion
The addition of square roots, while seemingly complex, can be greatly simplified using an adding square roots calculator. This tool is essential for students, educators, and anyone dealing with mathematical operations involving square roots. Here are some key takeaways:
- Ease of Use: By simply entering the square root values into the input fields and clicking calculate, you can quickly obtain the sum. This saves time and reduces the likelihood of errors.
- Accuracy: Calculators provide precise results, ensuring that your computations are accurate and reliable, which is particularly important for academic and professional work.
- Educational Value: Using a calculator helps in understanding the process of adding square roots by breaking down the steps and providing immediate feedback. This can enhance learning and comprehension of mathematical concepts.
- Versatility: These calculators can handle a wide range of values, making them useful for various practical applications, from simple homework problems to more complex engineering calculations.
In conclusion, the adding square roots calculator is a valuable tool that enhances mathematical accuracy and efficiency. It simplifies complex calculations, making it easier to learn and apply mathematical concepts in everyday situations. By incorporating this tool into your study or work routine, you can streamline your workflow and improve your problem-solving skills.
Hack Toán Căn Bậc Hai
READ MORE:
Hướng Dẫn Sử Dụng Máy Tính ClassWiz - Đại Số 4-1 Đơn Giản Hóa Căn Bậc Hai