Topic adding 2 square roots: Adding two square roots is a fundamental concept in algebra that involves combining like terms to simplify expressions. This guide provides a detailed explanation of the steps required to add square roots, including examples and practical tips to ensure you can handle these calculations with ease.
Table of Content
Adding Square Roots
When working with square roots, it's important to follow specific rules to add them correctly. The fundamental rule is that you can only add square roots with the same radicand, similar to how you add like terms in algebra.
Steps to Add Square Roots
- Simplify each square root if possible.
- Combine like terms (square roots with the same radicand).
Examples
Let's go through some examples to illustrate these steps:
Example 1: Adding Square Roots with the Same Radicand
Consider the expression:
\( 3\sqrt{5} + 2\sqrt{5} \)
Since both terms have the same radicand (5), we can add them directly:
\( 3\sqrt{5} + 2\sqrt{5} = 5\sqrt{5} \)
Example 2: Simplifying Before Adding
Consider the expression:
\( \sqrt{50} + \sqrt{18} \)
First, we simplify each square root:
- \( \sqrt{50} = \sqrt{25 \cdot 2} = 5\sqrt{2} \)
- \( \sqrt{18} = \sqrt{9 \cdot 2} = 3\sqrt{2} \)
Now, we add the simplified terms:
\( 5\sqrt{2} + 3\sqrt{2} = 8\sqrt{2} \)
Example 3: Adding and Subtracting Different Radicands
Consider the expression:
\( 4\sqrt{3} - 2\sqrt{3} \)
Since the radicands are the same (3), we can subtract them directly:
\( 4\sqrt{3} - 2\sqrt{3} = 2\sqrt{3} \)
Example 4: Combining Different Radicands After Simplification
Consider the expression:
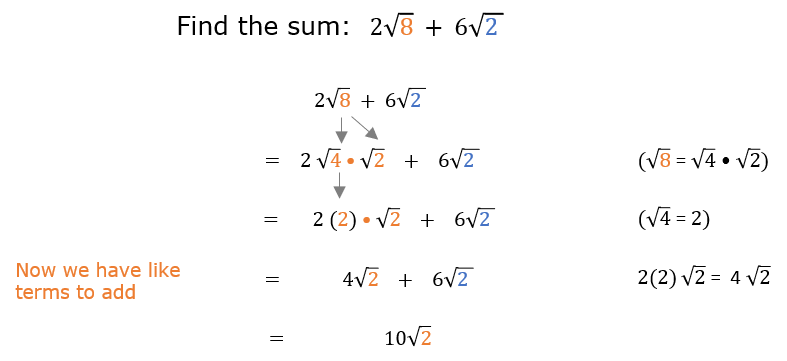
\( \sqrt{8} + \sqrt{2} \)
First, we simplify \( \sqrt{8} \):
\( \sqrt{8} = \sqrt{4 \cdot 2} = 2\sqrt{2} \)
Now, we can add the terms:
\( 2\sqrt{2} + \sqrt{2} = 3\sqrt{2} \)
By following these steps and examples, you can correctly add square roots by simplifying them first and then combining like terms.

READ MORE:
Understanding Square Roots
Square roots are fundamental concepts in mathematics, representing a value that, when multiplied by itself, yields the original number. Understanding square roots is essential for various mathematical operations, including solving equations and adding or subtracting radical expressions. Here, we will delve into the concept of square roots, how to simplify them, and their properties.
The square root of a number x is denoted as √x and is defined as the value y such that y2 = x. For example, √4 = 2 because 22 = 4.
Simplifying Square Roots
Simplifying square roots involves breaking down the radicand (the number under the square root symbol) into its prime factors and then simplifying. For instance, √18 can be simplified as follows:
- Factor the radicand into prime factors: 18 = 2 × 32.
- Rewrite the square root: √18 = √(2 × 32).
- Apply the square root to each factor: √18 = √2 × √32 = 3√2.
Properties of Square Roots
- Non-negative values: The principal square root of a non-negative number is always non-negative.
- Product property: The square root of a product is equal to the product of the square roots of the factors: √(a × b) = √a × √b.
- Quotient property: The square root of a quotient is equal to the quotient of the square roots of the numerator and denominator: √(a / b) = √a / √b, where b ≠ 0.
Adding and Subtracting Square Roots
Square roots can only be added or subtracted if they have the same radicand. For example, √2 + 3√2 = 4√2. If the radicands are different, simplification might be necessary first:
- Simplify each square root if possible.
- Add or subtract the coefficients of like radicals.
For instance, consider adding √12 + 2√3:
- Simplify √12: √12 = √(4 × 3) = 2√3.
- Now add the like terms: 2√3 + 2√3 = 4√3.
Examples
| √18 | = 3√2 |
| √50 | = 5√2 |
| √8 + 2√2 | = 2√2 + 2√2 = 4√2 |
Basic Principles of Adding Square Roots
Adding square roots involves a few essential steps to ensure accurate results. The process can be broken down into these main principles:
- Simplify each square root: Begin by simplifying the square roots, if possible. For example, the square root of 18 can be simplified to 3√2 because 18 = 9 × 2, and √9 = 3.
- Identify like terms: Like terms in square roots are those with the same radicand (the number inside the square root). For instance, 2√3 and 5√3 are like terms because they both contain √3.
- Add or subtract like terms: Once the square roots are simplified and like terms are identified, add or subtract the coefficients of the like terms. For example, 2√3 + 5√3 = 7√3.
Below is an example table illustrating these principles:
| Expression | Simplified Form | Result |
|---|---|---|
| √8 + 3√2 | 2√2 + 3√2 | 5√2 |
| √50 + 2√2 | 5√2 + 2√2 | 7√2 |
| 3√18 + √8 | 9√2 + 2√2 | 11√2 |
By following these steps, you can accurately add square roots, ensuring that only like terms are combined.
Examples of Adding Square Roots
Adding square roots can often be simplified if the radicands (the numbers inside the square root) are the same. Below are detailed examples that illustrate this process step by step.
- Example 1: Simple Addition of Like Terms
Consider the expression \( \sqrt{3} + 4\sqrt{3} \). Here, both terms have the same radicand, 3. So, we can add the coefficients directly:
\[
\sqrt{3} + 4\sqrt{3} = 1\sqrt{3} + 4\sqrt{3} = 5\sqrt{3}
\]
- Example 2: Simplifying Before Adding
Sometimes, it's necessary to simplify the square roots before adding. For example, consider \( \sqrt{8} + \sqrt{2} \). First, simplify \( \sqrt{8} \):
\[
\sqrt{8} = \sqrt{4 \cdot 2} = 2\sqrt{2}
\]
Now, the expression becomes:
\[
2\sqrt{2} + \sqrt{2} = 3\sqrt{2}
\]
- Example 3: Adding Simplified Terms
When given \( \sqrt{18} + 3\sqrt{2} \), start by simplifying \( \sqrt{18} \):
\[
\sqrt{18} = \sqrt{9 \cdot 2} = 3\sqrt{2}
\]
Now the expression is:
\[
3\sqrt{2} + 3\sqrt{2} = 6\sqrt{2}
\]
- Example 4: Combining Different Radicands
For the expression \( \sqrt{50} + 2\sqrt{2} \), simplify \( \sqrt{50} \) first:
\[
\sqrt{50} = \sqrt{25 \cdot 2} = 5\sqrt{2}
\]
The expression now is:
\[
5\sqrt{2} + 2\sqrt{2} = 7\sqrt{2}
\]
These examples illustrate the importance of simplifying square roots before adding them together to determine if they are like terms and can be combined.
Common Mistakes and How to Avoid Them
When adding square roots, certain pitfalls can lead to incorrect answers. Being aware of these common mistakes can significantly enhance your problem-solving skills and accuracy.
- Adding Unlike Radicands as Like Terms: A frequent error is treating square roots with different radicands as if they were like terms. Remember, \( \sqrt{2} + \sqrt{3} \) cannot be simplified to \( 2\sqrt{5} \) or any similar form because the radicands (2 and 3) are different.
- Incorrect Simplification: Missteps in simplifying square roots before adding them can derail the entire process. Ensure that you fully simplify each square root. For example, \( \sqrt{18} \) should be simplified to \( 3\sqrt{2} \), not left as is or incorrectly simplified.
- Ignoring Rationalization: Sometimes, you may need to rationalize the denominator when dealing with fractions that involve square roots. Overlooking this step can result in an incorrect final answer.
- Forgetting to Combine Coefficients: When square roots have the same radicand but different coefficients, make sure to combine the coefficients correctly. For instance, \( 3\sqrt{2} + 2\sqrt{2} \) equals \( 5\sqrt{2} \), not \( 3\sqrt{4} \) or any other incorrect combination.
- Overlooking Complex Numbers: When adding square roots of negative numbers, ensure to convert them into complex numbers correctly. For example, \( \sqrt{-1} \) should be represented as \( i \), and not as -1 or ignored altogether.
- Misapplying Decimal Approximations: Using decimal approximations for square roots can sometimes simplify calculations, but relying on them too heavily, especially in exact math problems, can introduce errors. Always check if an exact form is required.
Avoiding these common mistakes requires practice, attention to detail, and a solid understanding of the properties of square roots. Keeping these points in mind will help you navigate the complexities of adding square roots more confidently and accurately.

Advanced Techniques
When working with square roots, mastering advanced techniques can significantly improve your problem-solving skills. Here are some advanced strategies to enhance your understanding and efficiency:
- Memorize Key Square Roots: Knowing the square roots of numbers up to at least 15 can speed up the simplification process and make identifying like terms easier.
- Use the Conjugate for Rationalization: When rationalizing a denominator that includes a square root, multiply both the numerator and the denominator by the conjugate of the denominator to simplify effectively.
- Apply the Pythagorean Identity: In some cases, using the Pythagorean identity can simplify expressions involving square roots, especially in trigonometry.
- Explore Algebraic Identities: Familiarize yourself with algebraic identities that can simplify square root operations, such as the difference of squares.
- Practice with Complex Problems: Regularly challenge yourself with complex problems involving square roots to enhance your problem-solving skills and gain deeper insights into advanced techniques.
By incorporating these advanced techniques into your practice, you'll develop a more robust understanding of square roots and be better equipped to handle complex mathematical challenges.
Practice Problems and Solutions
Below are a series of practice problems to help you master the addition of square roots. Work through each problem and then check your solutions with the provided answers.
Problem Set 1: Basic Addition
-
Simplify: \( \sqrt{2} + \sqrt{2} \)
Solution: \( 2\sqrt{2} \)
-
Simplify: \( \sqrt{3} + 2\sqrt{3} \)
Solution: \( 3\sqrt{3} \)
-
Simplify: \( 4\sqrt{5} + 3\sqrt{5} \)
Solution: \( 7\sqrt{5} \)
Problem Set 2: Advanced Simplifications
-
Simplify: \( \sqrt{8} + \sqrt{18} \)
Solution:
- \( \sqrt{8} = 2\sqrt{2} \)
- \( \sqrt{18} = 3\sqrt{2} \)
- Combine: \( 2\sqrt{2} + 3\sqrt{2} = 5\sqrt{2} \)
Final Answer: \( 5\sqrt{2} \)
-
Simplify: \( 2\sqrt{12} + \sqrt{27} \)
Solution:
- \( 2\sqrt{12} = 2 \times 2\sqrt{3} = 4\sqrt{3} \)
- \( \sqrt{27} = 3\sqrt{3} \)
- Combine: \( 4\sqrt{3} + 3\sqrt{3} = 7\sqrt{3} \)
Final Answer: \( 7\sqrt{3} \)
-
Simplify: \( 3\sqrt{50} + 2\sqrt{32} \)
Solution:
- \( 3\sqrt{50} = 3 \times 5\sqrt{2} = 15\sqrt{2} \)
- \( 2\sqrt{32} = 2 \times 4\sqrt{2} = 8\sqrt{2} \)
- Combine: \( 15\sqrt{2} + 8\sqrt{2} = 23\sqrt{2} \)
Final Answer: \( 23\sqrt{2} \)
Solutions
Here are the detailed solutions for the practice problems:
| Problem | Solution |
|---|---|
| \( \sqrt{2} + \sqrt{2} \) | \( 2\sqrt{2} \) |
| \( \sqrt{3} + 2\sqrt{3} \) | \( 3\sqrt{3} \) |
| \( 4\sqrt{5} + 3\sqrt{5} \) | \( 7\sqrt{5} \) |
| \( \sqrt{8} + \sqrt{18} \) | \( 5\sqrt{2} \) |
| \( 2\sqrt{12} + \sqrt{27} \) | \( 7\sqrt{3} \) |
| \( 3\sqrt{50} + 2\sqrt{32} \) | \( 23\sqrt{2} \) |
Thêm hai căn bậc hai bằng cách đơn giản hóa
READ MORE:
Cách Cộng và Trừ Căn Bậc Hai