Topic how to add square roots with whole numbers: Adding square roots with whole numbers might seem challenging, but with the right approach, it becomes easy and straightforward. This guide will walk you through the process step-by-step, making sure you understand how to combine these numbers effectively. Whether you're a student or just curious, you'll find this information useful and engaging.
Table of Content
- How to Add Square Roots with Whole Numbers
- Introduction to Adding Square Roots and Whole Numbers
- Basic Concepts
- Identifying Whole Numbers and Square Roots
- Simplifying Square Roots
- Combining Whole Numbers and Simplified Square Roots
- Step-by-Step Guide to Addition
- Common Mistakes and How to Avoid Them
- Applications of Adding Square Roots and Whole Numbers
- Practice Problems and Solutions
- Conclusion
- YOUTUBE: Video hướng dẫn cách cộng và trừ căn bậc hai và số nguyên. Thích hợp cho những ai muốn học cách xử lý số căn bậc hai.
How to Add Square Roots with Whole Numbers
Adding square roots with whole numbers involves combining different mathematical concepts. Here's a step-by-step guide:
Step-by-Step Guide
-
Identify the Terms:
- Whole numbers are integers without fractions, e.g., \(2, 5, 8\).
- Square roots are values that, when multiplied by themselves, give the original number, e.g., \(\sqrt{4} = 2\).
-
Separate Whole Numbers and Square Roots:
- If you have an expression like \(5 + \sqrt{9}\), identify \(5\) as the whole number and \(\sqrt{9}\) as the square root.
-
Simplify the Square Root:
- Simplify \(\sqrt{9}\) to its whole number equivalent. Since \(\sqrt{9} = 3\), replace \(\sqrt{9}\) with \(3\).
-
Add the Simplified Square Root to the Whole Number:
- Now, add the simplified square root to the whole number: \(5 + 3\).
- The result is \(8\).
Example Problems
- Example 1:
Expression: \(7 + \sqrt{16}\)
Simplify: \(\sqrt{16} = 4\)
Add: \(7 + 4 = 11\)
- Example 2:
Expression: \(3 + \sqrt{25}\)
Simplify: \(\sqrt{25} = 5\)
Add: \(3 + 5 = 8\)
Special Cases
- If the square root is not a perfect square, it cannot be simplified to a whole number. For example, \(2 + \sqrt{5}\) remains as it is.
By following these steps, you can easily add square roots to whole numbers, provided the square root simplifies to a whole number.

READ MORE:
Introduction to Adding Square Roots and Whole Numbers
Adding square roots with whole numbers can initially seem complex, but it becomes manageable with a clear understanding of the concepts. This section provides a comprehensive introduction to help you master this skill.
To begin, it's essential to understand what square roots and whole numbers are:
- Whole Numbers: These are non-negative integers, including \(0, 1, 2, 3, \ldots\)
- Square Roots: A square root of a number \(x\) is a value that, when multiplied by itself, gives \(x\). For example, \(\sqrt{16} = 4\), because \(4 \times 4 = 16\).
When adding square roots and whole numbers, the process typically involves the following steps:
- Simplify the Square Root: If possible, simplify the square root to its simplest form. For example, \(\sqrt{9} = 3\).
- Identify the Whole Number: Recognize the whole number that is part of the expression.
- Combine the Values: Add the simplified square root value to the whole number.
Let's look at an example to illustrate these steps:
- Consider the expression \(7 + \sqrt{49}\).
- Simplify the Square Root: \(\sqrt{49} = 7\).
- Combine the Values: Add \(7\) (the whole number) to \(7\) (the simplified square root): \(7 + 7 = 14\).
In cases where the square root does not simplify to a whole number, the expression may be left as a sum of the whole number and the square root, such as \(3 + \sqrt{5}\).
Understanding these foundational steps will make the process of adding square roots and whole numbers straightforward and intuitive.
Basic Concepts
Understanding how to add square roots with whole numbers starts with grasping some basic mathematical concepts. This section breaks down these foundational ideas to make the process clear and approachable.
Whole Numbers
Whole numbers are non-negative integers. They include:
- 0
- 1
- 2
- 3
- And so on...
Square Roots
A square root of a number is a value that, when multiplied by itself, yields the original number. For example:
- \(\sqrt{4} = 2\) because \(2 \times 2 = 4\)
- \(\sqrt{9} = 3\) because \(3 \times 3 = 9\)
Simplifying Square Roots
Not all square roots simplify to whole numbers. For instance, \(\sqrt{2}\) is an irrational number and cannot be simplified further. However, square roots of perfect squares, like 4, 9, and 16, simplify to whole numbers.
Adding Square Roots to Whole Numbers
When adding square roots to whole numbers, follow these steps:
- Simplify the Square Root: If the square root can be simplified to a whole number, do so. For example, \(\sqrt{25} = 5\).
- Add the Whole Number: Combine the whole number with the simplified square root. For instance, if you have \(3 + \sqrt{25}\), it simplifies to \(3 + 5 = 8\).
- Leave as Is if Not Simplifiable: If the square root cannot be simplified to a whole number, leave the expression as is. For example, \(2 + \sqrt{3}\) remains \(2 + \sqrt{3}\).
Example Problem
Consider the expression \(6 + \sqrt{36}\):
- Simplify the Square Root: \(\sqrt{36} = 6\).
- Add the Whole Number: \(6 + 6 = 12\).
With these basic concepts in mind, adding square roots and whole numbers becomes a straightforward process.
Identifying Whole Numbers and Square Roots
To successfully add square roots and whole numbers, it is essential to identify and distinguish between these two types of numbers. This section provides a detailed explanation of how to do so.
Whole Numbers
Whole numbers are the set of non-negative integers, including zero. They are straightforward to identify because they do not include fractions or decimals. Examples of whole numbers are:
- 0
- 1
- 2
- 10
- 100
Square Roots
A square root of a number is a value that, when multiplied by itself, results in the original number. Square roots can be either whole numbers or irrational numbers. Here’s how to identify them:
- Perfect Squares: Numbers like 1, 4, 9, 16, and 25 are perfect squares. Their square roots are whole numbers:
- \(\sqrt{1} = 1\)
- \(\sqrt{4} = 2\)
- \(\sqrt{9} = 3\)
- \(\sqrt{16} = 4\)
- \(\sqrt{25} = 5\)
- Non-Perfect Squares: Numbers like 2, 3, 5, 7, and 8 are not perfect squares. Their square roots are irrational numbers:
- \(\sqrt{2} \approx 1.414\)
- \(\sqrt{3} \approx 1.732\)
- \(\sqrt{5} \approx 2.236\)
- \(\sqrt{7} \approx 2.646\)
- \(\sqrt{8} \approx 2.828\)
Combining Whole Numbers and Square Roots
When faced with an expression involving both whole numbers and square roots, identify each component clearly:
- Whole Number Component: Directly recognizable as a whole number (e.g., 3, 7, 10).
- Square Root Component: Recognizable by the radical sign (√) and can often be simplified if it's a perfect square (e.g., \(\sqrt{36}\) simplifies to 6).
By clearly identifying the whole numbers and square roots in an expression, you can effectively simplify and add them, leading to accurate results.
Simplifying Square Roots
Simplifying square roots is a crucial step when adding them to whole numbers. Simplifying involves finding the simplest form of a square root, which often makes addition more straightforward. This section explains the process step by step.
Understanding Perfect Squares
Perfect squares are numbers that have integer square roots. For example:
- \(1 = 1 \times 1\)
- \(4 = 2 \times 2\)
- \(9 = 3 \times 3\)
- \(16 = 4 \times 4\)
- \(25 = 5 \times 5\)
If the number under the square root (the radicand) is a perfect square, its square root simplifies to a whole number.
Steps to Simplify Square Roots
Follow these steps to simplify a square root:
- Identify the Radicand: The number inside the square root symbol. For example, in \(\sqrt{18}\), the radicand is 18.
- Factor the Radicand: Break down the radicand into its prime factors. For example, \(18 = 2 \times 3 \times 3\).
- Pair the Factors: Group the factors into pairs of identical numbers. For example, \(18 = (3 \times 3) \times 2\).
- Simplify the Square Root: For each pair of identical factors, take one factor out of the square root. For example, \(\sqrt{18} = \sqrt{(3 \times 3) \times 2} = 3\sqrt{2}\).
Example Problems
Let's look at a few examples to illustrate the simplification process:
- \(\sqrt{50}\)
- Factor the radicand: \(50 = 2 \times 5 \times 5\)
- Pair the factors: \((5 \times 5) \times 2\)
- Simplify: \(\sqrt{50} = 5\sqrt{2}\)
- \(\sqrt{72}\)
- Factor the radicand: \(72 = 2 \times 2 \times 2 \times 3 \times 3\)
- Pair the factors: \((2 \times 2) \times (3 \times 3) \times 2\)
- Simplify: \(\sqrt{72} = 6\sqrt{2}\)
- \(\sqrt{45}\)
- Factor the radicand: \(45 = 3 \times 3 \times 5\)
- Pair the factors: \((3 \times 3) \times 5\)
- Simplify: \(\sqrt{45} = 3\sqrt{5}\)
Special Cases
Sometimes, the radicand is not a perfect square and cannot be factored into pairs of identical numbers. In such cases, the square root remains in its simplified form. For example, \(\sqrt{7}\) and \(\sqrt{3}\) cannot be simplified further.
By mastering these steps, you can simplify square roots easily, making it more manageable to add them to whole numbers.
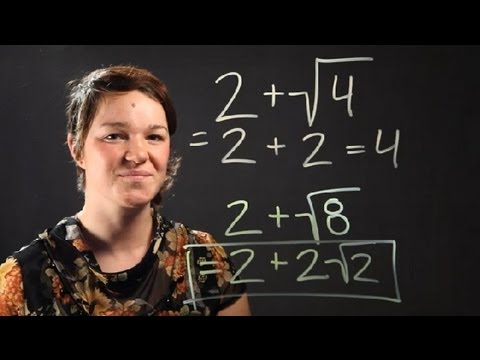
Combining Whole Numbers and Simplified Square Roots
Adding whole numbers and simplified square roots involves clear identification and systematic calculation. This section outlines the detailed steps to combine these elements effectively.
Step-by-Step Process
- Identify the Whole Number and Square Root:
Given an expression, separate the whole number from the square root. For example, in \(3 + \sqrt{16}\), identify \(3\) as the whole number and \(\sqrt{16}\) as the square root.
- Simplify the Square Root:
Simplify the square root if possible. For instance, \(\sqrt{16}\) simplifies to \(4\) because \(4 \times 4 = 16\).
- Add the Whole Number and Simplified Square Root:
Combine the whole number with the simplified square root. Continuing the example, add \(3\) and \(4\):
\(3 + 4 = 7\)
Example Problems
- Example 1:
Expression: \(5 + \sqrt{9}\)
- Identify the components: Whole number = \(5\), Square root = \(\sqrt{9}\)
- Simplify the square root: \(\sqrt{9} = 3\)
- Combine: \(5 + 3 = 8\)
- Example 2:
Expression: \(2 + \sqrt{25}\)
- Identify the components: Whole number = \(2\), Square root = \(\sqrt{25}\)
- Simplify the square root: \(\sqrt{25} = 5\)
- Combine: \(2 + 5 = 7\)
- Example 3:
Expression: \(4 + \sqrt{36}\)
- Identify the components: Whole number = \(4\), Square root = \(\sqrt{36}\)
- Simplify the square root: \(\sqrt{36} = 6\)
- Combine: \(4 + 6 = 10\)
Non-Simplifiable Square Roots
If the square root cannot be simplified to a whole number, the expression remains in its original form. For example:
- Expression: \(3 + \sqrt{5}\)
- Since \(\sqrt{5}\) is not a perfect square, it cannot be simplified further. The expression remains as \(3 + \sqrt{5}\).
By following these steps, you can accurately combine whole numbers with simplified square roots, simplifying and adding them where possible to achieve the correct result.
Step-by-Step Guide to Addition
Adding square roots with whole numbers may seem daunting at first, but by following a systematic approach, you can simplify the process. This guide provides a detailed step-by-step method to ensure accuracy.
Step 1: Identify Components
Separate the whole number and the square root in the expression. For example, in \(4 + \sqrt{25}\), identify \(4\) as the whole number and \(\sqrt{25}\) as the square root.
Step 2: Simplify the Square Root
Determine if the square root can be simplified to a whole number:
- If the radicand (the number inside the square root) is a perfect square, simplify it. For instance, \(\sqrt{25} = 5\).
- If the radicand is not a perfect square, it remains in its simplified form. For example, \(\sqrt{7}\) cannot be simplified further.
Step 3: Perform the Addition
- Simplified Square Roots: If the square root simplifies to a whole number, add this value to the existing whole number. For example, \(4 + \sqrt{25}\) becomes \(4 + 5 = 9\).
- Non-Simplifiable Square Roots: If the square root cannot be simplified to a whole number, the expression remains as a sum of the whole number and the square root. For example, \(3 + \sqrt{2}\) remains \(3 + \sqrt{2}\).
Example Problems
- Example 1: \(7 + \sqrt{49}\)
- Identify components: Whole number = \(7\), Square root = \(\sqrt{49}\)
- Simplify the square root: \(\sqrt{49} = 7\)
- Add: \(7 + 7 = 14\)
- Example 2: \(5 + \sqrt{16}\)
- Identify components: Whole number = \(5\), Square root = \(\sqrt{16}\)
- Simplify the square root: \(\sqrt{16} = 4\)
- Add: \(5 + 4 = 9\)
- Example 3: \(2 + \sqrt{10}\)
- Identify components: Whole number = \(2\), Square root = \(\sqrt{10}\)
- Simplify the square root: \(\sqrt{10}\) cannot be simplified further.
- Expression remains: \(2 + \sqrt{10}\)
Practice Problems
Try these problems on your own to reinforce your understanding:
- \(6 + \sqrt{36}\)
- \(8 + \sqrt{20}\)
- \(4 + \sqrt{9}\)
- \(3 + \sqrt{12}\)
By following these steps, you can confidently add square roots with whole numbers, simplifying and calculating accurately.
Common Mistakes and How to Avoid Them
Adding square roots with whole numbers can be tricky, and there are several common mistakes that learners often make. Here are some of the most frequent errors and how to avoid them:
-
Misunderstanding the Addition of Square Roots:
One of the most common mistakes is attempting to add square roots directly, as you would with whole numbers. For example, trying to add \( \sqrt{4} + \sqrt{9} \) as \( \sqrt{4+9} \) is incorrect.
Correction: Instead, evaluate each square root separately and then add the results. Here, \( \sqrt{4} = 2 \) and \( \sqrt{9} = 3 \), so \( \sqrt{4} + \sqrt{9} = 2 + 3 = 5 \).
-
Incorrect Simplification of Square Roots:
Another frequent error is incorrect simplification of square roots. For instance, mistaking \( \sqrt{8} \) for \( 2 \sqrt{2} \).
Correction: Properly simplify the square root by finding the prime factors. For \( \sqrt{8} \), write it as \( \sqrt{4 \times 2} = \sqrt{4} \cdot \sqrt{2} = 2\sqrt{2} \).
-
Adding Square Roots and Whole Numbers Directly:
Attempting to directly combine square roots and whole numbers without simplification. For example, \( 3 + \sqrt{16} \neq 3 + 16 \).
Correction: Simplify the square root first. \( \sqrt{16} = 4 \), so \( 3 + \sqrt{16} = 3 + 4 = 7 \).
-
Forgetting to Simplify Completely:
Sometimes students simplify square roots partially and then stop. For example, simplifying \( \sqrt{50} \) to \( 5\sqrt{2} \) but not simplifying further.
Correction: Ensure complete simplification by breaking it down into prime factors. \( \sqrt{50} = \sqrt{25 \times 2} = 5\sqrt{2} \).
By being mindful of these common mistakes and following the correct steps, you can accurately add square roots and whole numbers. Always simplify square roots fully before combining them with whole numbers, and double-check your work to avoid errors.
Applications of Adding Square Roots and Whole Numbers
Adding square roots and whole numbers may seem like a purely academic exercise, but it has various practical applications in different fields. Here are some examples:
- Finance: In finance, the volatility of stock prices is often calculated using the square root of the variance of stock returns. This helps investors assess risk and make informed decisions.
- Architecture: Engineers use square roots to determine the natural frequency of structures, such as bridges and buildings, to predict their response to various loads like wind and traffic.
- Science: Square roots are used in calculating physical quantities such as velocity, radiation levels, and sound intensity. These calculations are essential in research and technological development.
- Statistics: In statistics, the standard deviation, a measure of data variability, is the square root of the variance. This metric helps in analyzing data and drawing meaningful conclusions.
- Geometry: Square roots are fundamental in geometry for solving problems involving areas, perimeters, and the Pythagorean theorem, which relates to right triangles.
- Computer Science: In computer programming, square roots are used in algorithms for encryption, image processing, and game physics, playing a crucial role in data security and graphics.
- Cryptography: Square roots are employed in creating digital signatures and secure communication systems, ensuring the authenticity and confidentiality of data transactions.
- Navigation: Navigators use square roots to calculate distances between points on maps or globes, aiding in route planning and direction estimation.
- Electrical Engineering: Square roots are used to calculate power, voltage, and current in electrical circuits, essential for designing efficient and safe electrical systems.
- Cooking: When scaling recipes, the square root of the scaling factor helps maintain the correct proportions of ingredients, ensuring consistency in flavor and texture.
- Photography: The f-number in camera lenses, which controls light entry, involves square roots. Adjusting the f-number affects the light exposure in photography.
- Computer Graphics: Calculations involving distances and vector lengths in 2D and 3D graphics often use square roots, contributing to realistic rendering and animation.
- Telecommunication: Signal strength in wireless communication decreases with distance, following the inverse square law, where square roots are used to model this relationship.

Practice Problems and Solutions
Below are several practice problems to help you master the addition of square roots with whole numbers. Follow the steps carefully and use the solutions to check your work.
-
Problem 1: Simplify and add \( \sqrt{25} + 4 \).
Solution:
\[
\sqrt{25} = 5
\]
\[
5 + 4 = 9
\] -
Problem 2: Simplify and add \( 3 + \sqrt{9} \).
Solution:
\[
\sqrt{9} = 3
\]
\[
3 + 3 = 6
\] -
Problem 3: Add \( \sqrt{16} + \sqrt{4} + 7 \).
Solution:
\[
\sqrt{16} = 4
\]
\[
\sqrt{4} = 2
\]
\[
4 + 2 + 7 = 13
\] -
Problem 4: Simplify and add \( \sqrt{49} + 6 + \sqrt{36} \).
Solution:
\[
\sqrt{49} = 7
\]
\[
\sqrt{36} = 6
\]
\[
7 + 6 + 6 = 19
\] -
Problem 5: Add \( 5 + \sqrt{81} + 2 \).
Solution:
\[
\sqrt{81} = 9
\]
\[
5 + 9 + 2 = 16
\]
Continue practicing with more problems to build your confidence:
-
Problem 6: Simplify and add \( \sqrt{100} + 8 \).
Solution:
\[
\sqrt{100} = 10
\]
\[
10 + 8 = 18
\] -
Problem 7: Add \( \sqrt{144} + 12 + \sqrt{9} \).
Solution:
\[
\sqrt{144} = 12
\]
\[
\sqrt{9} = 3
\]
\[
12 + 12 + 3 = 27
\]
Conclusion
Adding square roots with whole numbers is a fundamental concept in algebra that builds upon understanding both square roots and whole numbers individually. It is crucial to simplify square roots whenever possible and identify like terms to ensure accurate calculations. By following the proper steps, including simplifying square roots and correctly combining them with whole numbers, students can master this skill effectively.
Throughout this guide, we've explored the basic concepts, identified common mistakes, and worked through various examples and special cases. We've also looked at practical applications and provided practice problems to reinforce learning.
Remember, the key to success in adding square roots with whole numbers lies in practice and careful attention to detail. Simplify where possible, combine like terms, and always double-check your work. By doing so, you will build a strong foundation in algebra and enhance your overall mathematical proficiency.
As you continue your studies, keep in mind the importance of these concepts and their applications in more advanced mathematics and real-world scenarios. With dedication and practice, you will find that adding square roots with whole numbers becomes an intuitive and straightforward process.
Video hướng dẫn cách cộng và trừ căn bậc hai và số nguyên. Thích hợp cho những ai muốn học cách xử lý số căn bậc hai.
Cách Cộng & Trừ Căn Bậc Hai & Số Nguyên: Số Căn Bậc Hai
READ MORE:
Video hướng dẫn cách cộng và trừ căn bậc hai một cách chi tiết và dễ hiểu. Thích hợp cho người học muốn nắm vững cách xử lý căn bậc hai.
Cách Cộng và Trừ Căn Bậc Hai