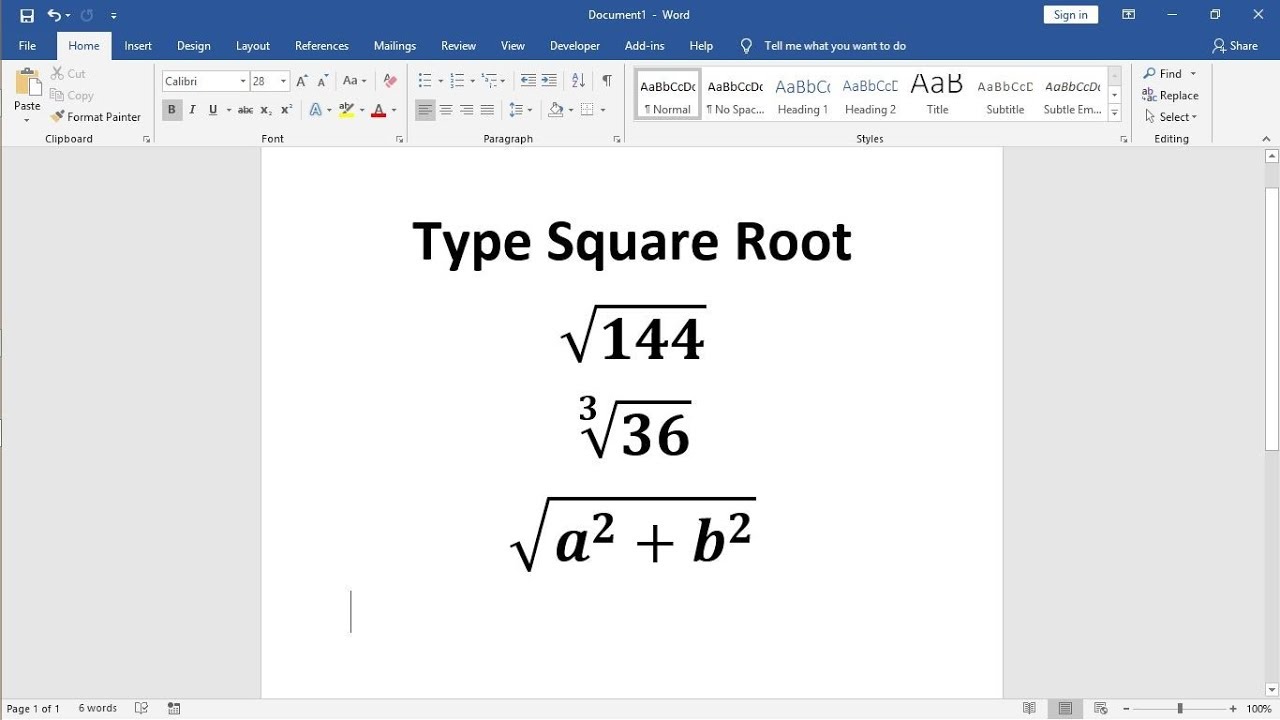
Topic 4 square roots: Discover the essential guide to understanding 4 square roots, from basic concepts to advanced applications. This comprehensive article will explore methods of calculation, properties, and real-life uses, providing you with a solid foundation and deeper insights into the fascinating world of square roots. Perfect for students, educators, and math enthusiasts alike.
Table of Content
- Understanding the 4 Square Roots
- Introduction to Square Roots
- Understanding the Concept of Square Roots
- Definition of Square Roots
- Properties of Square Roots
- Square Root of a Number
- Methods to Calculate Square Roots
- Prime Factorization Method
- Long Division Method
- Approximation Method
- Using a Calculator for Square Roots
- Perfect Squares and Their Square Roots
- Examples of Perfect Squares
- Non-Perfect Squares
- Finding Square Roots of Non-Perfect Squares
- Square Roots in Geometry
- Square Roots in Algebra
- Square Roots in Real Life
- Special Cases of Square Roots
- YOUTUBE: Video hỏi bạn có nhớ các căn bậc hai của những số chính phương bằng tiếng Việt để thu hút người xem và phù hợp với bài viết về '4 square roots'.
Understanding the 4 Square Roots
The concept of square roots is fundamental in mathematics. When we talk about "4 square roots," we are usually referring to the square roots of a number, considering both positive and negative solutions. Here, we will delve into the details and explore the concept using examples and mathematical explanations.
Definition and Basic Properties
The square root of a number \( x \) is a value that, when multiplied by itself, gives \( x \). Formally, if \( y = \sqrt{x} \), then \( y^2 = x \). Every positive real number \( x \) has two square roots: one positive (\( \sqrt{x} \)) and one negative (\( -\sqrt{x} \)).
Perfect Squares and Their Roots
Perfect squares are numbers that are the squares of integers. For example, 1, 4, 9, 16, and 25 are perfect squares because:
- \( 1 = 1^2 \)
- \( 4 = 2^2 \)
- \( 9 = 3^2 \)
- \( 16 = 4^2 \)
- \( 25 = 5^2 \)
The square roots of these numbers are:
- \( \sqrt{1} = \pm 1 \)
- \( \sqrt{4} = \pm 2 \)
- \( \sqrt{9} = \pm 3 \)
- \( \sqrt{16} = \pm 4 \)
- \( \sqrt{25} = \pm 5 \)
Calculating Square Roots
For numbers that are not perfect squares, calculating square roots can be more complex. Methods include prime factorization, approximation, and the use of a calculator. For example:
\(\sqrt{27}\) can be simplified as follows:
Principal Square Root
In most contexts, the principal square root refers to the positive square root. When using the radical symbol (\( \sqrt{} \)), it typically denotes the non-negative root. For example:
However, it is important to remember that the equation \( x^2 = 25 \) has two solutions: \( x = 5 \) and \( x = -5 \).
Applications of Square Roots
Square roots are widely used in various fields such as engineering, physics, statistics, and finance. They are crucial in solving quadratic equations, analyzing geometric shapes, and in algorithms for computer science.
Visual Representation
Graphically, the function \( f(x) = \sqrt{x} \) represents the principal square root and is defined for \( x \geq 0 \). The graph of \( f(x) = \sqrt{x} \) is a curve that increases slowly as \( x \) increases:
The graph is concave down, indicating that the rate of increase of \( f(x) \) decreases as \( x \) increases.
Common Misunderstandings
A common misunderstanding is that negative numbers do not have real square roots. In the real number system, this is true because the square of a real number cannot be negative. However, in the complex number system, negative numbers do have square roots. For example:
where \( i \) is the imaginary unit.
Understanding square roots and their properties is essential for advancing in mathematics and its applications in various scientific disciplines.

READ MORE:
Introduction to Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. It is one of the fundamental operations in mathematics and is denoted by the radical symbol \( \sqrt{} \). For example, the square root of 16 is 4, since \( 4 \times 4 = 16 \).
Square roots can be categorized into two types: perfect square roots and non-perfect square roots.
- Perfect Square Roots: These are the square roots of perfect squares, which are integers. For example, the square root of 25 is 5, since \( 5 \times 5 = 25 \).
- Non-Perfect Square Roots: These are the square roots of numbers that are not perfect squares. They are often irrational numbers. For example, the square root of 2 is approximately 1.414, and it cannot be expressed as a precise fraction.
Here are some important properties of square roots:
- The square root of 0 is 0: \( \sqrt{0} = 0 \).
- The square root of 1 is 1: \( \sqrt{1} = 1 \).
- Square roots of negative numbers are not real numbers. Instead, they are expressed in terms of imaginary numbers. For example, \( \sqrt{-1} = i \), where \( i \) is the imaginary unit.
- The product of square roots: \( \sqrt{a} \times \sqrt{b} = \sqrt{a \times b} \).
- The quotient of square roots: \( \frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}} \).
Square roots are used in various fields such as geometry, algebra, and calculus. Understanding how to calculate and apply them is crucial for solving mathematical problems.
To illustrate the concept further, consider the following examples:
| \( \sqrt{9} \) | = 3 |
| \( \sqrt{16} \) | = 4 |
| \( \sqrt{25} \) | = 5 |
| \( \sqrt{2} \) | \(\approx 1.414\) |
| \( \sqrt{3} \) | \(\approx 1.732\) |
By mastering the basics of square roots, you lay the groundwork for more advanced mathematical concepts and problem-solving techniques.
Understanding the Concept of Square Roots
Square roots are a fundamental mathematical operation that finds a number which, when multiplied by itself, results in the original number. The square root symbol is \( \sqrt{} \), and the square root of a number \( x \) is written as \( \sqrt{x} \).
To grasp the concept of square roots, consider the following step-by-step explanations:
-
Definition:
The square root of a number \( x \) is a number \( y \) such that \( y^2 = x \). In other words, \( \sqrt{x} = y \) if and only if \( y \times y = x \).
-
Perfect Squares:
Perfect squares are numbers that have integer square roots. For example:
- \( \sqrt{16} = 4 \), because \( 4 \times 4 = 16 \).
- \( \sqrt{25} = 5 \), because \( 5 \times 5 = 25 \).
-
Non-Perfect Squares:
For non-perfect squares, the square roots are irrational numbers. These cannot be expressed as exact fractions and their decimal representations are non-terminating and non-repeating. For example:
- \( \sqrt{2} \approx 1.414 \)
- \( \sqrt{3} \approx 1.732 \)
-
Negative Numbers:
Square roots of negative numbers involve imaginary numbers. The imaginary unit is denoted as \( i \), where \( i = \sqrt{-1} \). For instance:
- \( \sqrt{-4} = 2i \)
- \( \sqrt{-9} = 3i \)
Square roots also follow certain properties that make calculations easier:
- \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \)
- \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \)
- \( (\sqrt{a})^2 = a \)
Let's look at a few more examples to understand square roots better:
| \( \sqrt{81} \) | = 9 |
| \( \sqrt{144} \) | = 12 |
| \( \sqrt{0.25} \) | = 0.5 |
| \( \sqrt{0.01} \) | = 0.1 |
Understanding the concept of square roots provides a crucial foundation for more advanced mathematical topics and practical applications. Mastering this concept will enhance your ability to solve various mathematical problems efficiently.
Definition of Square Roots
The square root of a number is a value that, when multiplied by itself, yields the original number. It is denoted by the radical symbol \( \sqrt{} \). For a given number \( x \), the square root is written as \( \sqrt{x} \), and it satisfies the equation \( (\sqrt{x})^2 = x \).
To understand the definition of square roots in detail, consider the following steps:
-
Basic Definition:
The square root of a non-negative number \( x \) is a number \( y \) such that \( y^2 = x \). This means that \( y \times y = x \). For example, \( \sqrt{36} = 6 \) because \( 6 \times 6 = 36 \).
-
Positive and Negative Roots:
Every positive number has two square roots: a positive root and a negative root. However, by convention, the symbol \( \sqrt{} \) refers to the principal (positive) square root. For example:
- \( \sqrt{25} = 5 \)
- The other square root is \( -5 \) because \( (-5) \times (-5) = 25 \).
-
Perfect and Non-Perfect Squares:
A perfect square is a number that is the square of an integer. The square roots of perfect squares are integers. For instance:
- \( \sqrt{49} = 7 \)
- \( \sqrt{64} = 8 \)
Non-perfect squares are numbers that are not the square of an integer, and their square roots are irrational numbers. For example:
- \( \sqrt{2} \approx 1.414 \)
- \( \sqrt{3} \approx 1.732 \)
-
Square Roots of Negative Numbers:
Square roots of negative numbers are not real numbers. Instead, they are expressed using the imaginary unit \( i \), where \( i = \sqrt{-1} \). For instance:
- \( \sqrt{-4} = 2i \)
- \( \sqrt{-9} = 3i \)
Here are some examples to further illustrate the concept:
| \( \sqrt{100} \) | = 10 |
| \( \sqrt{121} \) | = 11 |
| \( \sqrt{144} \) | = 12 |
| \( \sqrt{0.04} \) | = 0.2 |
By understanding the definition of square roots, you gain a crucial foundation for further mathematical learning and problem-solving. Square roots are not only essential in basic arithmetic but also play a significant role in various advanced mathematical concepts.
Properties of Square Roots
Square roots possess several important properties that make them useful in various mathematical calculations. Understanding these properties can help simplify complex expressions and solve equations more efficiently.
Here are the key properties of square roots:
-
Non-Negative Property:
The square root of a non-negative number is always non-negative. This means \( \sqrt{x} \geq 0 \) for any \( x \geq 0 \). For example, \( \sqrt{9} = 3 \) and \( \sqrt{0} = 0 \).
-
Product Property:
The square root of a product is equal to the product of the square roots of the factors. Mathematically, this is expressed as:
\( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \)
For example, \( \sqrt{36 \times 25} = \sqrt{36} \times \sqrt{25} = 6 \times 5 = 30 \).
-
Quotient Property:
The square root of a quotient is equal to the quotient of the square roots of the numerator and the denominator. This is written as:
\( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \)
For instance, \( \sqrt{\frac{49}{9}} = \frac{\sqrt{49}}{\sqrt{9}} = \frac{7}{3} \).
-
Power Property:
The square root of a number raised to an even power returns the number raised to half that power. This can be stated as:
\( \sqrt{a^2} = a \)
For example, \( \sqrt{4^2} = 4 \) and \( \sqrt{10^2} = 10 \).
-
Square of Square Roots:
The square of the square root of a number returns the original number. Mathematically, this is:
\( (\sqrt{a})^2 = a \)
For instance, \( (\sqrt{5})^2 = 5 \) and \( (\sqrt{12})^2 = 12 \).
-
Addition and Subtraction:
The square root of a sum or difference cannot be simplified into the sum or difference of square roots. This means:
\( \sqrt{a + b} \neq \sqrt{a} + \sqrt{b} \)
\( \sqrt{a - b} \neq \sqrt{a} - \sqrt{b} \)
For example, \( \sqrt{4 + 9} = \sqrt{13} \neq \sqrt{4} + \sqrt{9} = 2 + 3 \).
Let's review some examples that demonstrate these properties:
| \( \sqrt{64 \times 25} \) | = \( \sqrt{64} \times \sqrt{25} = 8 \times 5 = 40 \) |
| \( \sqrt{\frac{81}{16}} \) | = \( \frac{\sqrt{81}}{\sqrt{16}} = \frac{9}{4} \) |
| \( (\sqrt{7})^2 \) | = 7 |
| \( \sqrt{100 + 25} \) | = \( \sqrt{125} \neq \sqrt{100} + \sqrt{25} = 10 + 5 \) |
Understanding these properties allows you to manipulate and simplify expressions involving square roots effectively, providing a solid foundation for tackling more advanced mathematical problems.

Square Root of a Number
The square root of a number is a value that, when multiplied by itself, gives the original number. It is represented using the radical symbol √ or the exponent (1/2). For example, the square root of 4 is written as √4 or 41/2.
To understand this concept more clearly, consider the number 4. The square roots of 4 are 2 and -2, since both 2² = 4 and (-2)² = 4. Generally, for any positive number n, there are two square roots: √n and -√n.
The principal (or positive) square root is the non-negative root, and it's often implied when we refer to the square root without specifying the sign. For example:
- The principal square root of 9 is 3 because 3² = 9.
- The negative square root of 9 is -3 because (-3)² = 9.
Properties of Square Roots
- Non-negativity: The principal square root of a non-negative number is always non-negative.
- Multiplication: The square root of a product is the product of the square roots of the factors. For example, √(a × b) = √a × √b.
- Division: The square root of a quotient is the quotient of the square roots of the numerator and the denominator. For example, √(a/b) = √a / √b.
- Powers: The square root of a number raised to an even power is the number raised to half that power. For example, √(a&sup4;) = a².
Example Calculations
Let's calculate the square root of 25:
- Identify a number that, when multiplied by itself, equals 25.
- Both 5 and -5 satisfy this condition because 5² = 25 and (-5)² = 25.
- Thus, √25 = 5 and -√25 = -5.
Approximation of Non-Perfect Squares
For numbers that are not perfect squares, we can approximate the square root. For instance, to find √6:
- Identify two perfect squares between which 6 lies: 4 (2²) and 9 (3²).
- Estimate the value closer to 6. We know 2.4² = 5.76 and 2.5² = 6.25.
- Thus, √6 is approximately 2.449, confirmed using a calculator.
Square roots are fundamental in mathematics and have applications in various fields, including geometry, algebra, and real-life problem-solving.
Methods to Calculate Square Roots
There are several methods to calculate the square root of a number. Below are detailed explanations of some common methods:
Prime Factorization Method
- Identify the prime factors of the given number.
- Group the prime factors into pairs of equal factors.
- Select one factor from each pair.
- Multiply the selected factors to obtain the square root.
Example: Find the square root of 324.
Prime factors of 324: \( 2 \times 2 \times 3 \times 3 \times 3 \times 3 \)
Grouping into pairs: \( (2 \times 2) \times (3 \times 3) \times (3 \times 3) \)
Selecting one factor from each pair: \( 2 \times 3 \times 3 = 18 \)
Thus, the square root of 324 is 18.
Repeated Subtraction Method
This method is applicable only to perfect squares. It involves subtracting consecutive odd numbers from the number until the result is zero. The number of subtractions performed gives the square root.
Example: Find the square root of 36 using repeated subtraction.
- 36 - 1 = 35
- 35 - 3 = 32
- 32 - 5 = 27
- 27 - 7 = 20
- 20 - 9 = 11
- 11 - 11 = 0
Since six subtractions were performed, the square root of 36 is 6.
Long Division Method
The long division method is useful for finding the square root of large numbers. Follow these steps:
- Draw lines at the top and to the left of the number.
- Group the digits of the number in pairs, starting from the decimal point or the rightmost digit.
- Find the largest number whose square is less than or equal to the first group.
- Subtract the square of this number from the first group and bring down the next group of digits.
- Double the quotient obtained and use it as the new divisor. Repeat the process until all groups are processed.
Example: Find the square root of 7225 using long division.
Pairs: 72 and 25.
- The largest number whose square is less than 72 is 8 (since \(8^2 = 64\)).
- Subtract 64 from 72, giving 8, and bring down 25, making 825.
- Double 8 to get 16. Now find a number X such that \(160X \times X \leq 825\).
- X is 5, as \(1605 \times 5 = 8025\).
The quotient, 85, is the square root of 7225.
Approximation Method
The approximation method involves estimating the square root by iteratively averaging and adjusting. This method is helpful for non-perfect squares and quick estimations.
- Make an initial guess for the square root.
- Divide the number by the guess and take the average of the quotient and the guess.
- Repeat the process until the desired accuracy is achieved.
Example: Find the square root of 20.
Initial guess: 4.
- 20 / 4 = 5
- Averaging: (4 + 5) / 2 = 4.5
- 20 / 4.5 ≈ 4.444, Average: (4.5 + 4.444) / 2 ≈ 4.472
Thus, the square root of 20 is approximately 4.472.
These methods provide a comprehensive approach to finding the square root of any number, whether it is a perfect square or not.
Prime Factorization Method
The prime factorization method is a systematic way of finding the square root of a number by expressing it as a product of prime factors. Here’s a step-by-step guide to using this method:
-
Step 1: Prime Factorization
Start by dividing the number into its prime factors. This involves repeatedly dividing the number by the smallest prime number until all factors are prime. For example, let's find the prime factors of 400.
\[
400 = 2 \times 2 \times 2 \times 2 \times 5 \times 5
\] -
Step 2: Pair the Prime Factors
Group the prime factors into pairs of equal factors. For 400, the prime factors grouped into pairs are:
\[
(2 \times 2), (2 \times 2), (5 \times 5)
\] -
Step 3: Take One Factor from Each Pair
Take one factor from each pair. In our example, this would be:
\[
2, 2, 5
\] -
Step 4: Multiply the Factors Together
Multiply these factors together to find the square root of the original number. For 400, the calculation is:
\[
2 \times 2 \times 5 = 20
\]Thus, the square root of 400 is 20.
Here are a few more examples to illustrate the process:
- Example 1: Find the square root of 625.
- Example 2: Find the square root of 1024.
Prime factorization: \(625 = 5 \times 5 \times 5 \times 5\)
Grouping into pairs: \((5 \times 5), (5 \times 5)\)
Taking one factor from each pair: \(5, 5\)
Multiplying the factors: \(5 \times 5 = 25\)
Therefore, \(\sqrt{625} = 25\).
Prime factorization: \(1024 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2\)
Grouping into pairs: \((2 \times 2), (2 \times 2), (2 \times 2), (2 \times 2), (2 \times 2)\)
Taking one factor from each pair: \(2, 2, 2, 2, 2\)
Multiplying the factors: \(2 \times 2 \times 2 \times 2 \times 2 = 32\)
Therefore, \(\sqrt{1024} = 32\).
The prime factorization method is particularly useful for perfect squares but can be more complex for larger numbers or those with many prime factors. It is an efficient method to understand the intrinsic properties of numbers and their square roots.
Long Division Method
The long division method is a systematic way to find the square root of a number. This method involves dividing the number into pairs of digits starting from the decimal point and working towards the left and the right. Here is a step-by-step process to calculate the square root using the long division method:
-
Separate the Digits into Pairs: Start from the decimal point and move both left and right, pairing the digits. For example, to find the square root of 104976, separate it as 10, 49, 76.
-
Find the Largest Number: Find the largest number whose square is less than or equal to the leftmost pair. For 10, it is 3 because \(3^2 = 9\).
-
Subtract and Bring Down the Next Pair: Subtract the square of the number found from the leftmost pair and bring down the next pair of digits. In this case, subtract 9 from 10 to get 1, and bring down 49, making it 149.
-
Form a New Divisor: Double the current quotient and form a new divisor. For example, double 3 to get 6 and place it next to a digit that, when multiplied, gives a number less than or equal to 149. In this case, 62 * 2 = 124.
-
Repeat the Process: Subtract the result from the current dividend (149 - 124 = 25), bring down the next pair (76), and repeat the process using the new divisor (formed by doubling the current quotient and appending a suitable digit).
Continue this process until all pairs of digits have been used. The quotient obtained will be the square root of the original number. If dealing with decimals, add pairs of zeros to continue the division process for more accuracy.
Let's take an example to illustrate:
| Step | Operation | Result |
| 1 | Pair the digits: 10, 49, 76 | |
| 2 | Find largest square ≤ 10 (32 = 9) | 3 |
| 3 | Subtract 9 from 10 and bring down 49 | 149 |
| 4 | New divisor: 6_ (double the quotient and find suitable digit) | 62 |
| 5 | 62 * 2 = 124 | 124 |
| 6 | Subtract 124 from 149, bring down 76 | 2576 |
| 7 | New divisor: 64_ | 644 |
| 8 | 644 * 4 = 2576 | 0 (remainder) |
| 9 | Final quotient: 324 |
The square root of 104976 is 324.
Practice Problems:
- Find the square root of 12321 using the long division method.
- Find the square root of 65536 using the long division method.

Approximation Method
The approximation method is a practical approach to estimate the square root of a number, especially when the exact square root is not required. This method is useful in various fields, including engineering, finance, and everyday problem-solving. Here, we explore a step-by-step process to approximate square roots.
Steps to Approximate Square Roots
- Identify Nearest Perfect Squares:
Determine the perfect squares closest to the given number. For instance, if you need to find the square root of 20, the closest perfect squares are 16 (42) and 25 (52).
- Initial Guess:
Start with an initial guess based on the nearest perfect squares. For 20, a reasonable guess might be between 4 and 5.
- Linear Interpolation:
Use linear interpolation to refine your estimate. The formula for interpolation is:
\[
\text{Estimated Square Root} = a + \left(\frac{n - a^2}{b^2 - a^2}\right) \times (b - a)
\]Where \( n \) is the number, \( a \) and \( b \) are the integers whose squares are nearest to \( n \). For 20:
\[
\text{Estimated Square Root} = 4 + \left(\frac{20 - 16}{25 - 16}\right) \times (5 - 4) = 4 + \left(\frac{4}{9}\right) \times 1 = 4 + 0.44 = 4.44
\] - Refine the Estimate:
If greater accuracy is needed, refine the estimate further by using more precise methods such as the Newton-Raphson method.
Example: Approximate Square Root of 18
- Nearest Perfect Squares: 16 (42) and 25 (52).
- Initial Guess: Between 4 and 5.
- Interpolation Calculation:
\[
\text{Estimated Square Root} = 4 + \left(\frac{18 - 16}{25 - 16}\right) \times (5 - 4) = 4 + \left(\frac{2}{9}\right) \times 1 = 4 + 0.22 = 4.22
\]
Applications of Approximation Method
- Engineering: Quick estimates for material requirements.
- Finance: Approximating growth rates and projections.
- Everyday Calculations: Estimating distances or areas quickly.
Approximation methods provide a balance between speed and accuracy, making them invaluable in many practical scenarios.
Using a Calculator for Square Roots
Calculating square roots using a calculator is straightforward and efficient. Here is a step-by-step guide on how to use a calculator for finding square roots:
- Turn on the Calculator:
Ensure your calculator is on and functioning. Most modern calculators have a dedicated button for square root calculations.
- Locate the Square Root Button:
Find the button labeled with the square root symbol (√). This button is usually found among the scientific functions of the calculator.
- Input the Number:
Type in the number for which you want to find the square root. For example, to find the square root of 16, press 1 followed by 6.
- Press the Square Root Button:
After entering the number, press the square root button (√). The calculator will display the principal square root of the number. For example, √16 will display 4.
- Read the Result:
The result displayed is the principal square root. If you need the negative root, you can simply negate the result manually. For example, if √16 is 4, then the negative root is -4.
Here are some examples of using a calculator for square roots:
| Number | Square Root |
|---|---|
| 25 | 5 |
| 81 | 9 |
| 144 | 12 |
Using calculators for square roots simplifies the process and ensures accuracy, especially with larger or more complex numbers. Whether you are dealing with perfect squares or non-perfect squares, a calculator is a handy tool for quick and reliable results.
Perfect Squares and Their Square Roots
Perfect squares are numbers that are the square of an integer. The square root of a perfect square is always an integer. Below is a list of some perfect squares and their corresponding square roots:
| Number | Square Root |
|---|---|
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
| 36 | 6 |
| 49 | 7 |
| 64 | 8 |
| 81 | 9 |
| 100 | 10 |
The pattern of perfect squares continues indefinitely. To find the square root of a perfect square, you can use the following properties:
- The square root of a perfect square is always a whole number.
- For any positive integer n, the square root of n2 is n.
For example, the square root of 144 is 12, because 12 × 12 = 144.
Knowing these properties can help in simplifying expressions and solving equations involving square roots. Perfect squares are fundamental in various areas of mathematics, including algebra, geometry, and number theory.
Examples of Perfect Squares
Perfect squares are numbers that are the squares of integers. This means that a number is a perfect square if it can be expressed as the product of an integer with itself. Here are some examples of perfect squares:
- 1 = \(1 \times 1\) = \(1^2\)
- 4 = \(2 \times 2\) = \(2^2\)
- 9 = \(3 \times 3\) = \(3^2\)
- 16 = \(4 \times 4\) = \(4^2\)
- 25 = \(5 \times 5\) = \(5^2\)
- 36 = \(6 \times 6\) = \(6^2\)
- 49 = \(7 \times 7\) = \(7^2\)
- 64 = \(8 \times 8\) = \(8^2\)
- 81 = \(9 \times 9\) = \(9^2\)
- 100 = \(10 \times 10\) = \(10^2\)
These numbers are called perfect squares because their square roots are whole numbers. Below is a table showing more examples of perfect squares:
| Number | Square |
|---|---|
| 11 | \(11^2 = 121\) |
| 12 | \(12^2 = 144\) |
| 13 | \(13^2 = 169\) |
| 14 | \(14^2 = 196\) |
| 15 | \(15^2 = 225\) |
| 16 | \(16^2 = 256\) |
| 17 | \(17^2 = 289\) |
| 18 | \(18^2 = 324\) |
| 19 | \(19^2 = 361\) |
| 20 | \(20^2 = 400\) |
| 21 | \(21^2 = 441\) |
| 22 | \(22^2 = 484\) |
| 23 | \(23^2 = 529\) |
| 24 | \(24^2 = 576\) |
| 25 | \(25^2 = 625\) |
Recognizing perfect squares is useful in various areas of mathematics, including solving quadratic equations and simplifying radical expressions. The above examples demonstrate how integers can be squared to form perfect squares, making them a fundamental concept in arithmetic and algebra.

Non-Perfect Squares
Non-perfect squares are numbers that do not have an integer as their square root. The square root of a non-perfect square is always an irrational number, which means it cannot be expressed as a simple fraction and has a non-repeating, non-terminating decimal expansion.
For example:
- The square root of 2 (√2) is approximately 1.414213562..., which is an irrational number.
- The square root of 3 (√3) is approximately 1.732050807..., which is also an irrational number.
To understand why non-perfect squares have irrational roots, consider the properties of perfect squares:
- A perfect square is a number that is the square of an integer. For instance, 16 is a perfect square because it equals 42.
- In contrast, 15 is not a perfect square because there is no integer that, when squared, equals 15. The square root of 15 is an irrational number (√15 ≈ 3.872).
Methods to Approximate Square Roots of Non-Perfect Squares
There are several methods to approximate the square roots of non-perfect squares, including:
1. Long Division Method
- Group the digits in pairs, starting from the decimal point to the left and right.
- Find the largest number whose square is less than or equal to the first group.
- Subtract the square of this number from the first group, then bring down the next pair of digits.
- Double the number obtained in the quotient and determine the next digit by trial and error, ensuring that the product is less than or equal to the current remainder.
- Repeat the process to get more digits in the square root.
2. Iterative Approximation Method (e.g., Newton's Method)
- Start with an initial guess (x0) for the square root.
- Use the formula: xn+1 = (xn + (N / xn)) / 2, where N is the number whose square root is being calculated.
- Repeat the iteration until the desired level of accuracy is achieved.
3. Using a Calculator
Most scientific calculators have a square root function (√) which provides an easy and accurate way to find the square root of non-perfect squares. Simply enter the number and press the square root button.
Understanding the nature of non-perfect squares and their irrational roots is crucial in various mathematical and real-life applications, such as engineering, physics, and computer science.
Finding Square Roots of Non-Perfect Squares
Finding the square roots of non-perfect squares can be more challenging since the results are not whole numbers. There are several methods to approximate the square roots of such numbers. Here are the most common methods:
1. Estimation Method
This method involves estimating the square root by identifying two consecutive perfect squares between which the number lies.
- Identify the perfect squares closest to the given number. For example, for \( \sqrt{50} \), the perfect squares are 49 (\(7^2\)) and 64 (\(8^2\)).
- Since 50 is closer to 49, we estimate that \( \sqrt{50} \) is slightly more than 7.
We can further refine our estimate by averaging or using a more detailed approximation.
2. Using a Calculator
Calculators can provide a quick and accurate approximation of square roots.
- Locate the square root function, usually denoted as \( \sqrt{x} \) on your calculator.
- Enter the number and press the square root button to obtain the approximation. For example, \( \sqrt{50} \approx 7.071 \).
3. Iterative Approximation (Babylonian Method)
The Babylonian method (also known as Heron's method) is an ancient technique that iteratively improves the estimate.
- Start with an initial guess \( x_0 \). For \( \sqrt{50} \), a good starting point might be 7.
- Use the formula \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{50}{x_n} \right) \) to get a better approximation.
- Repeat the process until the desired accuracy is reached.
For instance, starting with \( x_0 = 7 \):
- First iteration: \( x_1 = \frac{1}{2} \left( 7 + \frac{50}{7} \right) = 7.071 \)
- Second iteration: \( x_2 = \frac{1}{2} \left( 7.071 + \frac{50}{7.071} \right) = 7.071 \) (converges quickly)
4. Graphical Method
The graphical method involves plotting the function \( y = \sqrt{x} \) and finding the corresponding y-value for the given x-value. This can be done using graphing software or manually on graph paper.
These methods provide different levels of accuracy and can be chosen based on the tools available and the required precision.
Square Roots in Geometry
Square roots play a fundamental role in various geometric applications. One of the most notable uses is in the context of right triangles, where the Pythagorean theorem is applied. The theorem states that for any right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides:
\[
a^2 + b^2 = c^2
\]
where \(a\) and \(b\) are the lengths of the legs of the triangle, and \(c\) is the length of the hypotenuse. Therefore, the length of the hypotenuse can be found using the square root:
\]
c = \sqrt{a^2 + b^2}
\]
Another application of square roots in geometry is the construction of geometric shapes using compass and straightedge techniques. One such construction is finding the square root of a line segment. The process involves the following steps:
- Draw a line segment AB of unit length.
- Extend the line segment to point C such that BC is equal to the length whose square root you want to find.
- Find the midpoint M of segment AC.
- Draw a semicircle with center M and radius MA (or MC).
- Draw a line perpendicular to AB at point B, intersecting the semicircle at point D.
- The length of segment BD is the square root of the length of BC.
This method leverages the properties of similar triangles and the power of a point theorem to construct square roots geometrically.
Square roots also appear in the context of circle geometry. For example, if you know the length of a chord and the radius of the circle, you can find the distance from the chord to the center of the circle using the following formula:
\[
d = \sqrt{r^2 - \left(\frac{l}{2}\right)^2}
\]
where \(d\) is the distance from the center of the circle to the chord, \(r\) is the radius of the circle, and \(l\) is the length of the chord.
In addition to these applications, square roots are crucial in trigonometry, where they help determine distances and angles in various geometric problems.
Square Roots in Algebra
Square roots play a fundamental role in algebra, appearing in various types of equations and expressions. Here, we will explore several key concepts involving square roots in algebra:
1. Simplifying Square Root Expressions
To simplify a square root expression, we aim to remove any perfect squares from under the radical sign. The product rule is essential for this process:
\[\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}\]
For example, to simplify \(\sqrt{50}\), we factor it into \(\sqrt{25 \cdot 2}\), which simplifies to \(5\sqrt{2}\).
2. Solving Equations with Square Roots
Square roots are often used to solve quadratic equations. The standard form of a quadratic equation is:
\[ax^2 + bx + c = 0\]
By using the quadratic formula, we can solve for \(x\):
\[x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\]
The term under the square root, \(b^2 - 4ac\), is called the discriminant and determines the nature of the roots.
3. Rationalizing Denominators
When an expression has a square root in the denominator, it is often simplified by rationalizing the denominator. For instance, to rationalize \(\frac{1}{\sqrt{2}}\), we multiply the numerator and the denominator by \(\sqrt{2}\):
\[\frac{1}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}\]
4. Solving Radical Equations
Equations involving square roots, known as radical equations, can be solved by isolating the radical and then squaring both sides of the equation. For example, to solve:
\[\sqrt{x + 3} = 5\]
First, isolate the radical:
\[\sqrt{x + 3} = 5\]
Then, square both sides:
\[(\sqrt{x + 3})^2 = 5^2\]
This simplifies to:
\[x + 3 = 25\]
Solving for \(x\) gives:
\[x = 22\]
5. Applications in Functions
Square root functions are commonly analyzed in algebra. The basic form is:
\[f(x) = \sqrt{x}\]
The graph of this function is a curve that starts at the origin (0, 0) and increases gradually to the right, representing that the function is defined for non-negative \(x\) values only.
6. Practical Applications
- Geometry: Calculating distances using the Pythagorean theorem, where the hypotenuse is found using square roots.
- Physics: Determining time and distance in uniformly accelerated motion equations.
- Statistics: Standard deviation calculations often involve square roots.
Understanding and manipulating square roots is vital for solving a wide range of algebraic problems, and their applications extend far beyond pure mathematics into various fields of science and engineering.

Square Roots in Real Life
Square roots are not just theoretical concepts confined to mathematics textbooks; they have numerous practical applications in real life. Here are some examples:
-
Construction and Architecture:
Square roots are used to determine dimensions and measurements in construction projects. For example, when calculating the diagonal length of a rectangular space, the Pythagorean theorem (which involves square roots) is applied.
If a room has a length of 12 feet and a width of 5 feet, the diagonal can be found using the formula:
\[ d = \sqrt{l^2 + w^2} = \sqrt{12^2 + 5^2} = \sqrt{144 + 25} = \sqrt{169} = 13 \text{ feet} \] -
Physics and Engineering:
In physics, square roots are used in formulas to calculate various parameters. For instance, the speed of an object under constant acceleration is given by:
\[ v = \sqrt{2ad} \]
where \( v \) is the final velocity, \( a \) is the acceleration, and \( d \) is the distance traveled. -
Finance:
Square roots are used in financial modeling to calculate the volatility of stock prices and to assess risk. The standard deviation, which measures the amount of variation or dispersion of a set of values, involves square roots.
-
Agriculture:
Farmers use square roots to determine the appropriate spacing of crops. If a farmer wants to plant crops in a square grid, knowing the area of the field helps in determining the distance between each plant.
-
Medical Imaging:
Square roots are used in various medical imaging technologies, such as MRI and CT scans, to reconstruct images from raw data. The algorithms that process these images often involve calculations with square roots.
-
Navigation:
The distance between two points in a plane can be calculated using the distance formula, which is derived from the Pythagorean theorem:
\[ D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
This is essential in navigation and for plotting courses in aviation and maritime travel. -
Sound and Light:
Square roots are used in the calculations of sound intensity and light intensity. For example, the inverse square law states that the intensity of light or sound is inversely proportional to the square of the distance from the source.
Understanding the practical applications of square roots enhances our comprehension of the world and aids in solving real-world problems efficiently.
Special Cases of Square Roots
Square roots are fundamental in mathematics, but there are several special cases that require particular attention. These cases include dealing with negative numbers, zero, and perfect squares.
Square Root of Negative Numbers
In the set of real numbers, the square root of a negative number is undefined. This is because no real number squared gives a negative result. For example, there is no real number that satisfies the equation:
\[
x^2 = -9
\]
However, in the set of complex numbers, the square root of a negative number is defined using the imaginary unit \(i\), where \(i^2 = -1\). Thus, the square root of -9 can be expressed as:
\[
\sqrt{-9} = \sqrt{9} \cdot \sqrt{-1} = 3i
\]
Square Root of Zero
The square root of zero is a special case where the result is uniquely defined:
\[
\sqrt{0} = 0
\]
This is because \(0 \times 0 = 0\), making zero its own square root.
Perfect Squares
A perfect square is a number that has an integer as its square root. For instance, 16 is a perfect square because:
\[
\sqrt{16} = 4 \quad \text{and} \quad 4^2 = 16
\]
Other examples include 25, 36, and 49, where:
- \[ \sqrt{25} = 5 \quad \text{and} \quad 5^2 = 25 \]
- \[ \sqrt{36} = 6 \quad \text{and} \quad 6^2 = 36 \]
- \[ \sqrt{49} = 7 \quad \text{and} \quad 7^2 = 49 \]
Non-Perfect Squares
Non-perfect squares are numbers that do not have an integer as their square root. For example, the square root of 2 is an irrational number:
\[
\sqrt{2} \approx 1.414
\]
These roots cannot be expressed as a simple fraction and often require approximation or special methods for calculation.
Principal and Negative Roots
Every positive real number has two square roots: one positive (principal root) and one negative. For example, the two square roots of 25 are:
\[
\sqrt{25} = 5 \quad \text{and} \quad -\sqrt{25} = -5
\]
However, by convention, the radical sign \(\sqrt{}\) typically denotes the principal (positive) square root.
Summary of Special Cases
- Square root of negative numbers involves imaginary numbers (\(i\)).
- Square root of zero is zero.
- Perfect squares have integer roots.
- Non-perfect squares have irrational roots.
- Every positive number has a principal (positive) and negative square root.
Video hỏi bạn có nhớ các căn bậc hai của những số chính phương bằng tiếng Việt để thu hút người xem và phù hợp với bài viết về '4 square roots'.
Bạn Có Nhớ Các Căn Bậc Hai Của Những Số Chính Phương Này Không? 🤯 #Shorts #toán #toánhọc #toánhọc
READ MORE:
Video hướng dẫn cách đơn giản hóa căn bậc hai bằng tiếng Việt để thu hút người xem và phù hợp với bài viết về '4 square roots'.
Cách Đơn Giản Hóa Căn Bậc Hai