Topic adding square roots fractions: Understanding how to add square roots fractions is essential for mastering algebra and higher-level math. This guide will walk you through the steps of simplifying square roots, rationalizing denominators, and effectively adding or subtracting fractions involving square roots. Dive in to enhance your math skills and tackle complex expressions with confidence.
Table of Content
- Adding and Simplifying Square Roots and Fractions
- Introduction to Adding Square Roots
- Understanding Radicals and Fractions
- Step-by-Step Guide to Adding Square Roots with Fractions
- Simplifying Square Roots in Fractions
- Rationalizing the Denominator
- Examples and Practice Problems
- Common Mistakes to Avoid
- Advanced Techniques
- Practical Applications
- Additional Resources and Tools
- YOUTUBE: Xem video này để học cách thêm căn bậc hai vào phân số tử một cách dễ dàng và hiệu quả.
Adding and Simplifying Square Roots and Fractions
Understanding how to add and simplify square roots involving fractions is essential for mastering various mathematical concepts. Here are some key points and examples to guide you through the process.
Steps for Adding Square Roots
- Identify like terms: You can only add square roots if the radicands (the numbers inside the square root) are the same.
- Simplify square roots: Before adding, ensure each square root is in its simplest form.
- Add like terms: Once simplified, combine the coefficients of like terms.
Examples of Adding Square Roots
Example 1: \( \sqrt{5} + 2\sqrt{5} = 3\sqrt{5} \)
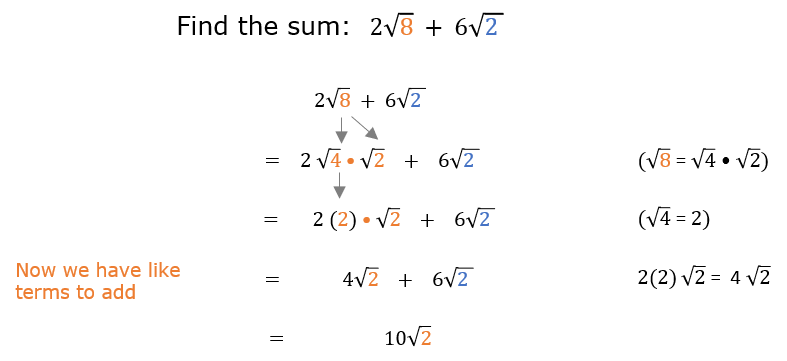
Example 2: \( 2\sqrt{8} + \sqrt{18} = 4\sqrt{2} + 3\sqrt{2} = 7\sqrt{2} \)
Example 3: \( \sqrt{9} + \sqrt{25} = 3 + 5 = 8 \) (simplified to whole numbers)
Simplifying Fractions with Square Roots
Simplifying fractions that include square roots can be broken down into a few clear steps:
- Simplify the Square Root: Simplify the numerator and the denominator separately.
- Rationalize the Denominator: If the denominator contains a square root, multiply the numerator and the denominator by the conjugate to eliminate the square root.
Examples of Simplifying Fractions with Square Roots
| Expression | Simplified Form |
|---|---|
| \( \frac{\sqrt{18}}{3} \) | \( \sqrt{2} \) |
| \( \frac{2}{\sqrt{12}} \) | \( \frac{\sqrt{3}}{3} \) |
| \( \frac{\sqrt{6}}{\sqrt{2}} \) | \( \sqrt{3} \) |
Rationalizing the denominator involves multiplying both the numerator and denominator by the conjugate of the denominator. For example, for the fraction \( \frac{5}{\sqrt{3}} \), you would multiply by \( \frac{\sqrt{3}}{\sqrt{3}} \) to get \( \frac{5\sqrt{3}}{3} \).
Practice Problems
- Simplify \( \frac{\sqrt{72}}{6} \)
- Rationalize \( \frac{3}{\sqrt{7}} \)
- Add \( 2\sqrt{3} + 4\sqrt{3} \)
With consistent practice, simplifying and adding square roots, especially those involving fractions, will become more intuitive. Remember to always simplify first and look for like terms when adding.

READ MORE:
Introduction to Adding Square Roots
Adding square roots can be a straightforward process if you understand the fundamental principles and follow a step-by-step approach. Square roots must be simplified and can only be combined if they are "like terms" - meaning they have the same radicand.
Here are the basic steps to add square roots:
- Simplify each square root as much as possible. For instance, simplify \(\sqrt{50}\) to \(5\sqrt{2}\).
- Combine like terms. Only square roots with the same radicand can be added together, such as \(3\sqrt{2} + 2\sqrt{2} = 5\sqrt{2}\).
For example:
| \(\sqrt{18} + \sqrt{8}\) | Simplify to \(3\sqrt{2} + 2\sqrt{2} = 5\sqrt{2}\) |
| \(2\sqrt{3} + 4\sqrt{3}\) | Combine to get \(6\sqrt{3}\) |
| \(\sqrt{50} + \sqrt{2}\) | Since \(\sqrt{50} = 5\sqrt{2}\), combine to get \(5\sqrt{2} + \sqrt{2} = 6\sqrt{2}\) |
Remember to always simplify the square roots first, and then determine if they can be combined as like terms. With practice, adding square roots will become a much more intuitive process.
Understanding Radicals and Fractions
Understanding how to work with radicals and fractions is essential in algebra. Radicals, often referred to as square roots, and fractions require careful handling to simplify expressions correctly.
Here is a step-by-step guide:
- Simplifying Radicals: Break down the number inside the square root into its prime factors. For example, \( \sqrt{50} \) can be simplified to \( \sqrt{25 \times 2} \), which equals \( 5\sqrt{2} \).
- Simplifying Fractions: Ensure the fraction is in its simplest form. For example, \( \frac{18}{50} \) simplifies to \( \frac{9}{25} \).
- Square Root of a Fraction: Apply the square root to both the numerator and the denominator separately. For instance, \( \sqrt{\frac{9}{25}} = \frac{\sqrt{9}}{\sqrt{25}} = \frac{3}{5} \).
- Combining Radicals: If you have multiple square roots, combine them carefully. \( \sqrt{a} + \sqrt{b} \) can only be combined if \( a \) and \( b \) are like terms. For example, \( \sqrt{18} + \sqrt{8} \) cannot be simplified further.
- Rationalizing Denominators: Ensure there are no radicals in the denominator. For example, \( \frac{1}{\sqrt{2}} \) can be rationalized to \( \frac{\sqrt{2}}{2} \) by multiplying the numerator and denominator by \( \sqrt{2} \).
By following these steps, you can effectively manage and simplify expressions involving radicals and fractions, leading to more accurate and simplified results in algebraic calculations.
Step-by-Step Guide to Adding Square Roots with Fractions
Adding square roots with fractions involves a clear understanding of both radicals and fraction operations. Below is a detailed step-by-step guide to help you master this process.
- Simplify Each Square Root
- Break down each square root into its simplest form. For example,
\(\sqrt{72} = \sqrt{36 \times 2} = 6\sqrt{2}\) .
- Break down each square root into its simplest form. For example,
- Find a Common Denominator
- If the fractions have different denominators, find a common denominator before proceeding. For example, to add
\(\frac{\sqrt{2}}{3}\) and \(\frac{\sqrt{3}}{4}\) , the common denominator would be 12.
- If the fractions have different denominators, find a common denominator before proceeding. For example, to add
- Adjust the Fractions
- Rewrite each fraction with the common denominator. For example,
\(\frac{\sqrt{2}}{3} = \frac{4\sqrt{2}}{12}\) and \(\frac{\sqrt{3}}{4} = \frac{3\sqrt{3}}{12}\) .
- Rewrite each fraction with the common denominator. For example,
- Add the Numerators
- Add the numerators while keeping the common denominator. For example,
\(\frac{4\sqrt{2}}{12} + \frac{3\sqrt{3}}{12} = \frac{4\sqrt{2} + 3\sqrt{3}}{12}\) .
- Add the numerators while keeping the common denominator. For example,
- Simplify the Result
- If possible, simplify the resulting fraction. This might involve rationalizing the denominator or combining like terms. For example, if the resulting fraction were
\(\frac{6\sqrt{2} + 3\sqrt{8}}{12}\) , you would simplify it by factoring and rationalizing.
- If possible, simplify the resulting fraction. This might involve rationalizing the denominator or combining like terms. For example, if the resulting fraction were
By following these steps, you can effectively add square roots that involve fractions, ensuring your final answer is in its simplest form.
Simplifying Square Roots in Fractions
Simplifying square roots in fractions involves a few key steps to ensure the expression is as simplified as possible. Here’s a detailed guide:
- Identify Perfect Squares:
First, check if the numerator and the denominator of the fraction have any perfect squares. Perfect squares include numbers like 4, 9, 16, 25, etc., which can be expressed as \(2^2\), \(3^2\), \(4^2\), and so on.
- Simplify the Fraction:
Reduce the fraction if possible to make the numbers smaller and easier to work with. For example:
\[
\frac{18}{50} = \frac{9}{25}
\] - Separate the Square Roots:
Use the property \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\) to separate the square roots in the fraction. For example:
\[
\sqrt{\frac{9}{25}} = \frac{\sqrt{9}}{\sqrt{25}} = \frac{3}{5}
\] - Simplify Each Square Root:
If either the numerator or the denominator is not a perfect square, try to simplify them. For example, to simplify \(\sqrt{45}\):
\[
\sqrt{45} = \sqrt{9 \times 5} = \sqrt{9} \times \sqrt{5} = 3\sqrt{5}
\] - Combine Results:
Once each part of the fraction is simplified, combine them back into a single fraction. For example, for \(\sqrt{\frac{8}{32}}\):
\[
\sqrt{\frac{8}{32}} = \sqrt{\frac{1}{4}} = \frac{\sqrt{1}}{\sqrt{4}} = \frac{1}{2}
\]
Using these steps will help you simplify square roots in fractions efficiently. Practice with different examples to become more familiar with the process.

Rationalizing the Denominator
Rationalizing the denominator is an important step when working with square roots in fractions. This process involves eliminating the square root from the denominator to make the fraction simpler to work with. Below is a detailed, step-by-step guide to rationalizing the denominator.
-
Identify the Square Root in the Denominator:
Let's start with a fraction that has a square root in the denominator, such as \(\frac{a}{\sqrt{b}}\).
-
Multiply by the Conjugate:
To remove the square root, multiply both the numerator and the denominator by the square root present in the denominator. This is essentially multiplying by 1, which does not change the value of the fraction.
For example, with \(\frac{a}{\sqrt{b}}\), multiply by \(\frac{\sqrt{b}}{\sqrt{b}}\):
\[
\frac{a}{\sqrt{b}} \times \frac{\sqrt{b}}{\sqrt{b}} = \frac{a\sqrt{b}}{b}
\] -
Simplify the Fraction:
After multiplying, the denominator no longer contains a square root, and the fraction is simplified.
For instance:
\[
\frac{5}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{5\sqrt{3}}{3}
\] -
Check for Further Simplification:
Ensure the fraction is in its simplest form. Sometimes, further simplification may be possible if both the numerator and denominator share common factors.
For example:
\[
\frac{2}{\sqrt{12}} = \frac{2}{2\sqrt{3}} = \frac{1}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{\sqrt{3}}{3}
\]
By following these steps, you can effectively rationalize the denominator in any fraction containing square roots, making them easier to work with in further calculations.
Examples and Practice Problems
Practicing the addition of square roots in fractions helps solidify your understanding. Below are examples and practice problems to guide you through the process.
-
Example 1: Add \(\frac{\sqrt{2}}{3}\) and \(\frac{\sqrt{2}}{6}\)
- Find a common denominator: 6.
- Rewrite the fractions: \(\frac{2\sqrt{2}}{6} + \frac{\sqrt{2}}{6}\).
- Add the numerators: \(\frac{2\sqrt{2} + \sqrt{2}}{6} = \frac{3\sqrt{2}}{6} = \frac{\sqrt{2}}{2}\).
-
Example 2: Add \(\frac{\sqrt{3}}{4}\) and \(\frac{\sqrt{12}}{8}\)
- Simplify \(\sqrt{12} = 2\sqrt{3}\).
- Rewrite the second fraction: \(\frac{2\sqrt{3}}{8} = \frac{\sqrt{3}}{4}\).
- Add the fractions: \(\frac{\sqrt{3}}{4} + \frac{\sqrt{3}}{4} = \frac{2\sqrt{3}}{4} = \frac{\sqrt{3}}{2}\).
-
Practice Problem 1: Add \(\frac{\sqrt{5}}{2}\) and \(\frac{\sqrt{20}}{4}\).
-
Practice Problem 2: Add \(\frac{\sqrt{7}}{3}\) and \(\frac{\sqrt{28}}{6}\).
-
Practice Problem 3: Add \(\frac{\sqrt{11}}{5}\) and \(\frac{\sqrt{44}}{10}\).
Work through these practice problems step by step, simplifying where necessary, and finding common denominators. The solutions will help reinforce the methods discussed in previous sections.
Common Mistakes to Avoid
When adding square roots with fractions, it's essential to be mindful of several common errors that can arise. By being aware of these mistakes, you can enhance your understanding and accuracy in performing these operations.
- Forgetting to Simplify Radicals: Before adding square roots, ensure that each radical is simplified as much as possible. Simplifying radicals involves finding perfect square factors of the radicand and simplifying them.
- Incorrectly Adding Radicals: Adding square roots is not the same as adding regular numbers. Avoid simply adding or subtracting the numbers under the radicals without considering the square root property.
- Misapplying Rules of Rationalizing Denominators: While rationalizing the denominator is a common practice in mathematics, misapplying this rule can lead to errors. Ensure that you rationalize the denominator correctly, especially when dealing with fractions containing square roots.
- Overlooking the Distribution Property: When adding square roots with fractions, it's crucial to remember the distribution property. Distributing a constant or variable across terms within a radical can significantly impact the final result.
- Skipping the Check for Extraneous Solutions: After performing addition or subtraction involving square roots, always check for extraneous solutions. Sometimes, solutions obtained may not be valid in the original context, necessitating a careful review.
By avoiding these common mistakes and practicing regularly, you can strengthen your skills in adding square roots with fractions and enhance your problem-solving abilities in mathematics.
Advanced Techniques
Mastering the addition of square roots with fractions opens the door to advanced techniques that can streamline calculations and deepen your understanding of mathematical concepts. Here are some advanced strategies to consider:
- Combining Like Terms: When adding expressions with square roots, identify and combine like terms to simplify the expression. This technique reduces the complexity of the problem and makes it easier to perform calculations.
- Utilizing Conjugates: Conjugates are expressions formed by changing the sign between two terms. They are particularly useful when rationalizing denominators containing square roots. By multiplying the numerator and denominator by the conjugate, you can eliminate radicals from the denominator and achieve a simplified expression.
- Applying the Pythagorean Theorem: The Pythagorean theorem is a fundamental concept in geometry that relates the lengths of the sides of a right triangle. This theorem can be applied in various scenarios involving square roots and fractions, providing elegant solutions to complex problems.
- Exploring Binomial Expansion: Binomial expansion allows you to expand expressions raised to a power into a series of terms. This technique can be applied to simplify expressions containing square roots, leading to a more manageable form for further manipulation.
- Employing Algebraic Manipulations: Algebraic manipulations, such as factoring and completing the square, can be powerful tools in simplifying expressions with square roots. By applying algebraic techniques, you can transform complex expressions into simpler forms, facilitating easier computation.
By incorporating these advanced techniques into your problem-solving repertoire, you can tackle more challenging mathematical problems with confidence and efficiency.

Practical Applications
The ability to add square roots with fractions has numerous practical applications across various fields, ranging from engineering to finance. Here are some real-world scenarios where this skill is invaluable:
- Engineering Calculations: In engineering, particularly in fields like civil engineering and mechanics, adding square roots with fractions is essential for calculating dimensions, distances, and forces. Engineers use these calculations to design structures, analyze materials, and ensure the safety and efficiency of projects.
- Physics Formulas: Many physics formulas involve square roots and fractions, especially in areas like mechanics, electromagnetism, and quantum mechanics. Understanding how to add square roots with fractions enables physicists to solve complex equations and model physical phenomena accurately.
- Financial Modeling: In finance, adding square roots with fractions is often encountered when calculating risk metrics, such as volatility and standard deviation. These calculations are crucial for assessing investment performance, pricing financial derivatives, and managing portfolios effectively.
- Computer Graphics and Image Processing: In computer graphics and image processing, square roots and fractions frequently appear in algorithms for rendering, image manipulation, and compression. Mastery of adding square roots with fractions allows programmers to optimize code performance and create visually stunning graphics.
- Statistical Analysis: Statistical analysis involves various mathematical operations, including adding square roots with fractions. Statisticians use these calculations to analyze data, conduct hypothesis tests, and make informed decisions in fields such as economics, sociology, and epidemiology.
By applying the principles of adding square roots with fractions in these practical settings, professionals can solve complex problems, make accurate predictions, and advance knowledge in their respective fields.
Additional Resources and Tools
Exploring additional resources and utilizing helpful tools can further enhance your understanding and proficiency in adding square roots with fractions. Here are some valuable resources and tools to support your learning:
- Mathematics Textbooks: Refer to comprehensive mathematics textbooks that cover topics such as algebra, trigonometry, and calculus. Many textbooks provide detailed explanations, examples, and practice problems related to adding square roots with fractions.
- Online Courses and Tutorials: Enroll in online courses or watch tutorials specifically focused on operations with square roots and fractions. Websites like Khan Academy, Coursera, and edX offer interactive lessons and exercises to help reinforce your skills.
- Mathematical Software: Utilize mathematical software programs such as Mathematica, MATLAB, or Maple to perform complex calculations involving square roots and fractions. These tools provide computational assistance and visualization capabilities.
- Math Forums and Communities: Participate in online forums and communities dedicated to mathematics, where you can ask questions, share insights, and collaborate with fellow learners and experts. Websites like Math Stack Exchange and Reddit's r/math are excellent platforms for seeking guidance and support.
- Practice Worksheets and Problem Sets: Practice solving a variety of problems related to adding square roots with fractions by completing worksheets and problem sets. Many educational websites and textbooks offer downloadable resources for additional practice.
By exploring these additional resources and utilizing helpful tools, you can reinforce your understanding of adding square roots with fractions and develop confidence in applying these skills to solve mathematical problems.
Xem video này để học cách thêm căn bậc hai vào phân số tử một cách dễ dàng và hiệu quả.
Cách Thêm Căn Bậc Hai vào Phân Số Tử
READ MORE:
Xem video này để thấy các ví dụ về cách cộng và trừ căn bậc hai trong đại số.
Ví dụ về Cộng và Trừ Căn Bậc Hai - Đại Số 1