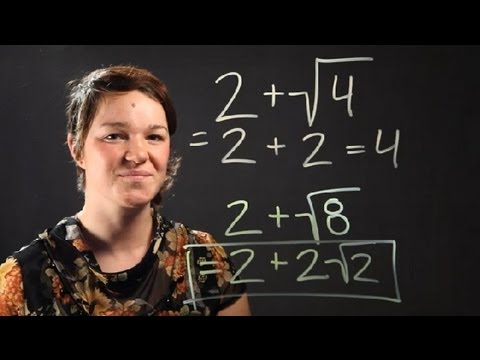Topic rules for adding square roots: Learning the rules for adding square roots is essential for mastering basic and advanced mathematical concepts. This guide will walk you through simplifying square roots, identifying like radicals, and applying practical techniques to add square roots correctly. Discover common mistakes to avoid and enhance your math skills with clear examples and practice problems.
Table of Content
- Rules for Adding Square Roots
- Introduction
- Understanding Square Roots
- Basic Rules for Adding Square Roots
- Simplifying Square Roots
- Identifying Like Radicals
- Steps to Add Square Roots
- Examples of Adding Square Roots
- Common Mistakes to Avoid
- Advanced Techniques
- Practical Applications
- Exercises and Practice Problems
- Summary and Conclusion
- YOUTUBE: How to Add and Subtract Square Roots
Rules for Adding Square Roots
Adding square roots involves specific rules and conditions to simplify the expressions effectively. Understanding these rules is crucial for accurate calculations in mathematics.
Basic Concept
The primary rule for adding square roots is that you can only add square roots with the same radicand (the number inside the square root symbol). For example, \(\sqrt{a} + \sqrt{a} = 2\sqrt{a}\), but \(\sqrt{a} + \sqrt{b}\) cannot be simplified further if \(a \neq b\).
Steps for Adding Square Roots
Simplify each square root: Ensure each square root is in its simplest form. For instance, \(\sqrt{18}\) can be simplified to \(3\sqrt{2}\).
Identify like terms: Group the square roots with the same radicand. For example, \(3\sqrt{2} + 5\sqrt{2}\) are like terms.
Add the coefficients of like terms: Combine the coefficients (numbers in front of the square root). For instance, \(3\sqrt{2} + 5\sqrt{2} = 8\sqrt{2}\).
Examples
- \(\sqrt{5} + 2\sqrt{5} = 3\sqrt{5}\)
- \(4\sqrt{7} + \sqrt{7} = 5\sqrt{7}\)
- \(2\sqrt{3} + 3\sqrt{3} = 5\sqrt{3}\)
- \(\sqrt{8} + \sqrt{2} = 2\sqrt{2} + \sqrt{2} = 3\sqrt{2}\) (simplify \(\sqrt{8}\) to \(2\sqrt{2}\))
Additional Notes
If the radicands are different, the square roots cannot be added directly. For instance, \(\sqrt{3} + \sqrt{5}\) remains unchanged because the radicands are different and cannot be simplified to a common term.
Table of Common Simplifications
| \(\sqrt{4}\) | \(2\) |
| \(\sqrt{9}\) | \(3\) |
| \(\sqrt{16}\) | \(4\) |
| \(\sqrt{25}\) | \(5\) |
Conclusion
Adding square roots requires recognizing and combining like terms. By simplifying and matching radicands, the process becomes straightforward and manageable. Always remember, unlike terms must be left as they are.
READ MORE:
Introduction
Understanding how to add square roots is crucial for mastering various mathematical concepts. Square roots can only be added when their radicands (the numbers inside the square root symbol) are identical. If the radicands are not the same, simplification may help in making them alike. Once simplified, square roots with the same radicands can be added by combining their coefficients. This introduction aims to provide a step-by-step approach to adding square roots effectively.
Understanding Square Roots
Square roots are fundamental in mathematics, representing a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3, because 3 × 3 = 9. The square root is denoted by the radical symbol √. The number under the radical is called the radicand.
Here are some key points to understand about square roots:
- Square roots of perfect squares (like 4, 9, 16) are whole numbers.
- Square roots of non-perfect squares are irrational numbers (e.g., √2, √3).
- Negative numbers do not have real square roots since no real number squared gives a negative value.
Simplifying Square Roots
To simplify square roots, factor the radicand into its prime factors and pair the identical factors.
- Example: Simplify √18.
- Factor 18 as 2 × 3 × 3.
- Pair the 3s and take one out of the radical: √18 = √(3 × 3 × 2) = 3√2.
- Example: Simplify √50.
- Factor 50 as 2 × 5 × 5.
- Pair the 5s and take one out of the radical: √50 = √(5 × 5 × 2) = 5√2.
Adding and Subtracting Square Roots
To add or subtract square roots, the radicands must be identical. Only like terms can be combined.
- Example: Add 3√2 + 5√2.
- Since the radicands are the same, combine the coefficients: 3√2 + 5√2 = 8√2.
- Example: Subtract 4√3 - 2√3.
- Since the radicands are the same, combine the coefficients: 4√3 - 2√3 = 2√3.
- Example: Add 3√2 + 2√3.
- The radicands are different, so the expression cannot be simplified further.
Basic Rules for Adding Square Roots
Adding square roots may seem complicated, but it can be broken down into simple, manageable steps. The key to success lies in understanding when square roots can be combined and how to simplify them before adding. Follow these fundamental rules to add square roots correctly:
- Simplify each square root: Before attempting to add, ensure each square root is in its simplest form. This might involve factoring out perfect squares from under the radical sign.
- Identify like terms: Square roots can only be added if they are "like terms," meaning they have the same radicand (the number under the square root symbol).
- Add the coefficients: Once the square roots are simplified and identified as like terms, add their coefficients (the numbers in front of the square roots).
Here is a step-by-step guide:
- Simplify each square root:
Example: Simplify \(5\sqrt{12} + 2\sqrt{3}\)
First, simplify \(5\sqrt{12}\). Recognize that 12 can be factored into \(4 \times 3\), so:
\(5\sqrt{12} = 5\sqrt{4 \times 3} = 5 \cdot 2\sqrt{3} = 10\sqrt{3}\)
Now, the expression is \(10\sqrt{3} + 2\sqrt{3}\).
- Identify like terms:
Since both terms now have \(\sqrt{3}\) as their radicand, they are like terms.
- Add the coefficients:
Add the coefficients (10 and 2):
\(10\sqrt{3} + 2\sqrt{3} = 12\sqrt{3}\)
It’s important to always simplify the square roots first before adding to ensure that you correctly identify the like terms. This process can help you manage more complex problems involving square roots with ease.
Simplifying Square Roots
Simplifying square roots is an essential step in various mathematical operations involving radicals. Simplifying helps in adding, subtracting, multiplying, and dividing square roots more efficiently. Here’s a detailed, step-by-step process to simplify square roots:
-
Identify Perfect Squares: Look for perfect square factors within the radicand (the number inside the square root symbol). For example, in , 18 can be factored into 9 and 2, where 9 is a perfect square.
-
Rewrite the Radicand: Express the radicand as a product of its factors. For , write it as .
-
Extract the Square Root: Take the square root of the perfect square factor out of the radical. becomes , which simplifies to .
-
Simplify Further if Possible: Check if the remaining radicand can be simplified further. If not, the expression is the simplest form of .
-
Combining Like Terms: When adding or subtracting square roots, ensure the terms have the same radicand. For instance, can be combined as because they share the same radicand.
By following these steps, you can simplify square roots and handle complex radical expressions more effectively.

Identifying Like Radicals
Identifying like radicals is a crucial step in simplifying and adding square roots. Like radicals have the same radicand (the number or expression inside the square root) and the same index (the degree of the root). Here’s a step-by-step guide to identifying and working with like radicals:
- Ensure the radicals have the same index. For square roots, the index is 2, but for cube roots or higher, the index will differ.
- Compare the radicands. The radicands must be identical for the radicals to be considered like radicals. For example, \(\sqrt{5}\) and \(3\sqrt{5}\) are like radicals because their radicands are both 5.
- If the radicands are not the same, check if they can be simplified to become like radicals. For instance, \(\sqrt{50}\) can be simplified to \(5\sqrt{2}\), which can then be combined with other \(\sqrt{2}\) terms.
Let's look at some examples to clarify:
- \(3\sqrt{2} + 5\sqrt{2}\): These are like radicals since they both have the radicand 2. Combine them by adding the coefficients: \(3 + 5 = 8\). The result is \(8\sqrt{2}\).
- \(4\sqrt{3} - 2\sqrt{3}\): Again, these are like radicals. Subtract the coefficients: \(4 - 2 = 2\). The result is \(2\sqrt{3}\).
- \(2\sqrt{7} + 3\sqrt{5}\): These are not like radicals as the radicands (7 and 5) are different. Therefore, they cannot be combined.
- \(6\sqrt{18} + 2\sqrt{2}\): Simplify \(\sqrt{18}\) to \(3\sqrt{2}\), so the expression becomes \(6 \times 3\sqrt{2} + 2\sqrt{2}\), which simplifies to \(18\sqrt{2} + 2\sqrt{2}\). Now, combine the like radicals: \(18 + 2 = 20\). The result is \(20\sqrt{2}\).
By following these steps, you can simplify expressions involving square roots more effectively, making it easier to perform operations like addition and subtraction on them.
Steps to Add Square Roots
Adding square roots can be simplified into a series of steps. Follow these steps carefully to ensure accurate results:
- Simplify Each Square Root: Begin by simplifying each square root to its simplest form. For example,
\(\sqrt{18} = 3\sqrt{2}\). - Identify Like Radicals: Ensure that the square roots you are adding have the same radicand (the number under the square root). Only like radicals can be added together. For instance,
\(\sqrt{2}\) and \(3\sqrt{2}\)can be added because they have the same radicand. - Combine Like Radicals: Add or subtract the coefficients (the numbers in front of the square roots) of the like radicals. For example,
\(\sqrt{2} + 3\sqrt{2} = 4\sqrt{2}\).
Let’s look at a specific example:
| Add | \(5\sqrt{12} + 2\sqrt{3}\) |
| Simplify: | \(5\sqrt{12} = 5\sqrt{4 \cdot 3} = 5 \cdot 2\sqrt{3} = 10\sqrt{3}\) |
| \(2\sqrt{3}\) remains the same. | |
| Combine: | \(10\sqrt{3} + 2\sqrt{3} = 12\sqrt{3}\) |
By following these steps, you can accurately add square roots and simplify your mathematical expressions efficiently.
Examples of Adding Square Roots
Adding square roots involves combining like terms, which are radicals that have the same radicand. Below are some detailed examples to illustrate the process step by step:
Example 1
Add \( \sqrt{2} + 3\sqrt{2} \)
- Identify like radicals: Both terms have the same radicand \( \sqrt{2} \).
- Combine the coefficients: \( 1\sqrt{2} + 3\sqrt{2} = (1+3)\sqrt{2} \)
- Simplify the expression: \( 4\sqrt{2} \)
Result: \( \sqrt{2} + 3\sqrt{2} = 4\sqrt{2} \)
Example 2
Add \( 2\sqrt{5} + 4\sqrt{5} + \sqrt{5} \)
- Identify like radicals: All terms have the same radicand \( \sqrt{5} \).
- Combine the coefficients: \( 2\sqrt{5} + 4\sqrt{5} + 1\sqrt{5} = (2+4+1)\sqrt{5} \)
- Simplify the expression: \( 7\sqrt{5} \)
Result: \( 2\sqrt{5} + 4\sqrt{5} + \sqrt{5} = 7\sqrt{5}
Example 3
Add \( \sqrt{3} + 2\sqrt{3} - \sqrt{3} \)
- Identify like radicals: All terms have the same radicand \( \sqrt{3} \).
- Combine the coefficients: \( 1\sqrt{3} + 2\sqrt{3} - 1\sqrt{3} = (1+2-1)\sqrt{3} \)
- Simplify the expression: \( 2\sqrt{3} \)
Result: \( \sqrt{3} + 2\sqrt{3} - \sqrt{3} = 2\sqrt{3} \)
Example 4
Add \( 3\sqrt{7} + 2\sqrt{7} + 5\sqrt{7} \)
- Identify like radicals: All terms have the same radicand \( \sqrt{7} \).
- Combine the coefficients: \( 3\sqrt{7} + 2\sqrt{7} + 5\sqrt{7} = (3+2+5)\sqrt{7} \)
- Simplify the expression: \( 10\sqrt{7} \)
Result: \( 3\sqrt{7} + 2\sqrt{7} + 5\sqrt{7} = 10\sqrt{7} \)
Example 5
Add \( 4\sqrt{2} + 3\sqrt{3} \)
- Identify like radicals: The terms have different radicands \( \sqrt{2} \) and \( \sqrt{3} \).
- Since the radicands are different, these radicals cannot be combined directly.
- The expression remains: \( 4\sqrt{2} + 3\sqrt{3} \)
Result: \( 4\sqrt{2} + 3\sqrt{3} \) cannot be simplified further as the radicals are different.
Common Mistakes to Avoid
When adding square roots, it's crucial to avoid common mistakes that can lead to incorrect results. Here are some key mistakes to watch out for and tips to ensure accuracy:
-
Adding Unlike Radicands Directly:
A common mistake is attempting to add square roots with different radicands as if they were like terms. Remember, you can only directly add square roots if their radicands are the same.
For example, \(\sqrt{2} + \sqrt{3} \neq \sqrt{5}\). These cannot be combined directly because their radicands are different.
-
Ignoring Simplification:
Not simplifying square roots before attempting to add them can lead to incorrect results. Always check if the square roots can be simplified to find like terms.
For instance, \(\sqrt{18} + \sqrt{8}\) should be simplified first: \(\sqrt{18} = 3\sqrt{2}\) and \(\sqrt{8} = 2\sqrt{2}\). Then, you can add them: \(3\sqrt{2} + 2\sqrt{2} = 5\sqrt{2}\).
-
Misapplying Coefficient Rules:
Another mistake is confusing the rules for adding coefficients with the rules for adding radicands. Coefficients in front of the square roots are added together, but the radicand must remain the same for direct addition to be possible.
For example, \(2\sqrt{3} + 3\sqrt{3} = 5\sqrt{3}\). However, \(2\sqrt{3} + 3\sqrt{5}\) cannot be simplified further because the radicands are different.
-
Forgetting to Rationalize the Denominator:
When adding fractions that involve square roots in the denominator, it's important to rationalize the denominators first to simplify the expression.
For example, \(\frac{1}{\sqrt{2}} + \frac{1}{\sqrt{3}}\) should be rationalized to \(\frac{\sqrt{2}}{2} + \frac{\sqrt{3}}{3}\) before attempting further addition or simplification.
-
Overlooking the Need for Factoring:
Missing out on perfect square factors within the radicand can prevent simplification. Always break down the radicand into its prime factors to find and extract perfect squares.
For example, \(\sqrt{50}\) should be simplified to \(5\sqrt{2}\) because \(50 = 25 \times 2\) and \(\sqrt{25} = 5\).
By being mindful of these common errors and adopting a methodical approach to simplifying and adding square roots, you can enhance your accuracy and confidence in handling these types of problems. Remember, practice makes perfect, so don't hesitate to work through several problems to solidify your understanding and skills.

Advanced Techniques
When it comes to adding square roots, advanced techniques can simplify complex expressions and solve problems more efficiently. These techniques often involve the use of algebraic identities, rationalization, and other mathematical strategies. Below are some advanced techniques to consider:
Using Algebraic Identities
One powerful method for simplifying the addition of square roots involves algebraic identities. For example:
- Difference of squares: \(a^2 - b^2 = (a + b)(a - b)\)
- Square of a binomial: \((a + b)^2 = a^2 + 2ab + b^2\)
These identities can help to simplify expressions before performing addition.
Rationalizing Denominators
In some cases, it's beneficial to rationalize the denominator when adding square roots, especially when dealing with fractions. The process involves multiplying the numerator and denominator by the conjugate of the denominator. For example:
To simplify \(\frac{\sqrt{a} + \sqrt{b}}{\sqrt{c}}\), multiply by \(\frac{\sqrt{c}}{\sqrt{c}}\) to get:
\[
\frac{(\sqrt{a} + \sqrt{b}) \cdot \sqrt{c}}{\sqrt{c} \cdot \sqrt{c}} = \frac{(\sqrt{a} \cdot \sqrt{c} + \sqrt{b} \cdot \sqrt{c})}{c}
\]
Combining Like Terms
Similar to adding like terms in algebra, combining like radicals simplifies the expression. For instance:
- \(\sqrt{2} + 3\sqrt{2} = 4\sqrt{2}\)
- \(5\sqrt{3} - 2\sqrt{3} = 3\sqrt{3}\)
This technique can greatly reduce the complexity of the problem.
Using Prime Factorization
Prime factorization can be an effective way to simplify square roots before adding them. For example:
To simplify \(\sqrt{50} + \sqrt{18}\), we first express each number in terms of its prime factors:
\[
\sqrt{50} = \sqrt{2 \cdot 5^2} = 5\sqrt{2}
\]
\[
\sqrt{18} = \sqrt{2 \cdot 3^2} = 3\sqrt{2}
\]
Then, add the simplified terms:
\[
5\sqrt{2} + 3\sqrt{2} = 8\sqrt{2}
\]
Using Nested Radicals
Nested radicals can often be simplified using specific formulas. For example:
To simplify \(\sqrt{a + \sqrt{b}}\), we might use the formula:
\[
\sqrt{a + \sqrt{b}} = \sqrt{\frac{a + \sqrt{a^2 - b}}{2}} + \sqrt{\frac{a - \sqrt{a^2 - b}}{2}}
\]
This technique requires identifying the appropriate values of \(a\) and \(b\).
Example Problem
Let's consider an example to illustrate these advanced techniques:
Simplify the expression: \(\sqrt{45} + \sqrt{20}\)
- Factorize each term:
- \(\sqrt{45} = \sqrt{3 \cdot 3 \cdot 5} = 3\sqrt{5}\)
- \(\sqrt{20} = \sqrt{2 \cdot 2 \cdot 5} = 2\sqrt{5}\)
- Combine like radicals:
\(3\sqrt{5} + 2\sqrt{5} = 5\sqrt{5}\)
By applying these advanced techniques, you can handle more complicated expressions involving the addition of square roots efficiently.
Practical Applications
Understanding how to add square roots is crucial not only in academic settings but also in various real-world applications. Here are some practical scenarios where the rules for adding square roots can be applied:
- Engineering and Physics: When dealing with wave functions, vibrations, and oscillations, engineers and physicists often need to add square roots. For example, combining different wave amplitudes involves adding square roots to determine resultant waves.
- Architecture and Construction: Calculating distances, areas, and materials often requires the use of square roots. For instance, when determining the lengths of the sides of right-angled triangles in construction plans, architects add square roots to ensure accurate measurements.
- Finance: In financial modeling, risk assessment often involves standard deviations and variances, which require the addition of square roots. This is essential in creating models that predict financial risk and returns.
- Computer Graphics: In graphics programming, adding square roots is vital for transformations and manipulations of shapes. For example, calculating the distance between points in 3D space involves adding square roots.
Let’s look at a detailed example involving a real-world application:
Example: Combining Forces in Physics
Suppose you are calculating the resultant force of two perpendicular forces acting on an object. If the magnitudes of the forces are represented as \( F_1 \) and \( F_2 \), the resultant force \( F_r \) can be found using the Pythagorean theorem:
\[ F_r = \sqrt{F_1^2 + F_2^2} \]
Let's assume \( F_1 = 3 \, \text{N} \) and \( F_2 = 4 \, \text{N} \). To find \( F_r \):
- First, square the magnitudes of each force:
- \( F_1^2 = 3^2 = 9 \)
- \( F_2^2 = 4^2 = 16 \)
- Add the squared values:
- \( 9 + 16 = 25 \)
- Finally, take the square root of the sum:
- \( F_r = \sqrt{25} = 5 \, \text{N} \)
So, the resultant force \( F_r \) is \( 5 \, \text{N} \).
Example: Distance Calculation in Coordinate Geometry
Consider finding the distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) on a plane. The distance \( d \) is given by:
\[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
If the points are \((1, 2)\) and \((4, 6)\), the calculation steps are:
- Calculate the differences in coordinates:
- \( x_2 - x_1 = 4 - 1 = 3 \)
- \( y_2 - y_1 = 6 - 2 = 4 \)
- Square the differences:
- \( 3^2 = 9 \)
- \( 4^2 = 16 \)
- Add the squared differences:
- \( 9 + 16 = 25 \)
- Take the square root of the sum:
- \( d = \sqrt{25} = 5 \)
Therefore, the distance between the points is \( 5 \) units.
Exercises and Practice Problems
Practice makes perfect! Below are several exercises to help you master the addition of square roots. Work through each problem and check your answers at the end.
Exercise 1: Basic Addition
- \(\sqrt{2} + \sqrt{2}\)
- \(\sqrt{3} + \sqrt{3}\)
- \(\sqrt{5} + \sqrt{5}\)
Exercise 2: Addition with Simplification
- \(\sqrt{8} + \sqrt{18}\)
- \(\sqrt{50} + \sqrt{32}\)
- \(\sqrt{45} + \sqrt{20}\)
Exercise 3: Identifying Like Radicals
- \(\sqrt{12} + \sqrt{27}\)
- \(\sqrt{8} + \sqrt{2}\)
- \(\sqrt{32} + \sqrt{50}\)
Exercise 4: Mixed Problems
- \(\sqrt{18} + \sqrt{8} + \sqrt{2}\)
- \(\sqrt{75} + \sqrt{12} + \sqrt{3}\)
- \(\sqrt{20} + \sqrt{45} + \sqrt{5}\)
Exercise 5: Advanced Addition
- \(\sqrt{72} + \sqrt{98} + \sqrt{18}\)
- \(\sqrt{50} + \sqrt{75} + \sqrt{27}\)
- \(\sqrt{12} + \sqrt{48} + \sqrt{75}\)
Answers
- Exercise 1:
- \(\sqrt{2} + \sqrt{2} = 2\sqrt{2}\)
- \(\sqrt{3} + \sqrt{3} = 2\sqrt{3}\)
- \(\sqrt{5} + \sqrt{5} = 2\sqrt{5}\)
- Exercise 2:
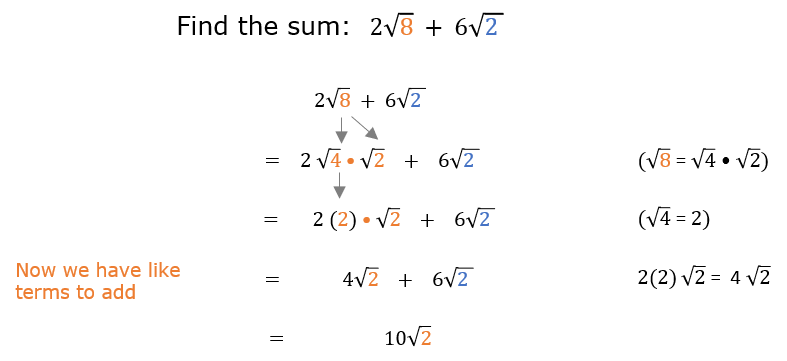
- \(\sqrt{8} + \sqrt{18} = 2\sqrt{2} + 3\sqrt{2} = 5\sqrt{2}\)
- \(\sqrt{50} + \sqrt{32} = 5\sqrt{2} + 4\sqrt{2} = 9\sqrt{2}\)
- \(\sqrt{45} + \sqrt{20} = 3\sqrt{5} + 2\sqrt{5} = 5\sqrt{5}\)
- Exercise 3:
- \(\sqrt{12} + \sqrt{27} = 2\sqrt{3} + 3\sqrt{3} = 5\sqrt{3}\)
- \(\sqrt{8} + \sqrt{2} = 2\sqrt{2} + \sqrt{2} = 3\sqrt{2}\)
- \(\sqrt{32} + \sqrt{50} = 4\sqrt{2} + 5\sqrt{2} = 9\sqrt{2}\)
- Exercise 4:
- \(\sqrt{18} + \sqrt{8} + \sqrt{2} = 3\sqrt{2} + 2\sqrt{2} + \sqrt{2} = 6\sqrt{2}\)
- \(\sqrt{75} + \sqrt{12} + \sqrt{3} = 5\sqrt{3} + 2\sqrt{3} + \sqrt{3} = 8\sqrt{3}\)
- \(\sqrt{20} + \sqrt{45} + \sqrt{5} = 2\sqrt{5} + 3\sqrt{5} + \sqrt{5} = 6\sqrt{5}\)
- Exercise 5:
- \(\sqrt{72} + \sqrt{98} + \sqrt{18} = 6\sqrt{2} + 7\sqrt{2} + 3\sqrt{2} = 16\sqrt{2}\)
- \(\sqrt{50} + \sqrt{75} + \sqrt{27} = 5\sqrt{2} + 5\sqrt{3} + 3\sqrt{3} = 5\sqrt{2} + 8\sqrt{3}\)
- \(\sqrt{12} + \sqrt{48} + \sqrt{75} = 2\sqrt{3} + 4\sqrt{3} + 5\sqrt{3} = 11\sqrt{3}\)
Summary and Conclusion
Adding square roots is a process that requires careful consideration of the terms involved. This guide has provided a comprehensive overview of the steps and rules necessary to add square roots successfully. Here's a summary of the key points:
- Square roots can only be added if they have the same radicand (the number under the square root). For example, \(\sqrt{3}\) and \(2\sqrt{3}\) can be added to get \(3\sqrt{3}\), but \(\sqrt{2}\) and \(\sqrt{3}\) cannot be directly added because their radicands are different.
- Before adding square roots, always simplify them if possible. Simplifying helps identify like terms. For instance, \(\sqrt{18}\) can be simplified to \(3\sqrt{2}\), making it possible to add with other terms involving \(\sqrt{2}\).
- When square roots have coefficients, the coefficients are added while keeping the square root part the same. For example, \(5\sqrt{12}\) and \(2\sqrt{3}\) can be simplified and then added as \(10\sqrt{3} + 2\sqrt{3} = 12\sqrt{3}\).
- In some cases, subtraction of square roots follows the same rules. Radicands must be the same, and the expressions should be simplified before performing the subtraction.
Here is a step-by-step process for adding square roots:
- Simplify each square root: Break down the radicand into its prime factors and simplify the square root if possible. For example, \(\sqrt{50}\) simplifies to \(5\sqrt{2}\).
- Identify like terms: After simplifying, identify square roots that have the same radicand. Only these like terms can be combined.
- Add the coefficients: Combine the coefficients of like terms while keeping the square root part the same. For instance, \(3\sqrt{2} + 4\sqrt{2} = 7\sqrt{2}\).
By following these steps, you can effectively add square roots and avoid common mistakes such as trying to add square roots with different radicands or forgetting to simplify before adding.
Understanding and applying these rules will enhance your skills in algebra and help you tackle more complex mathematical problems involving square roots. Practice with various examples and exercises to solidify your understanding and proficiency in adding square roots.

How to Add and Subtract Square Roots
Adding and Subtracting Radical Expressions With Square Roots and Cube Roots
Learn to add and subtract radical expressions
Adding and Subtracting Square Roots
UNDERSTAND Operations with SQUARE ROOTS in 10 minutes
Square Roots – the rules you need to know to solve problems…
READ MORE: