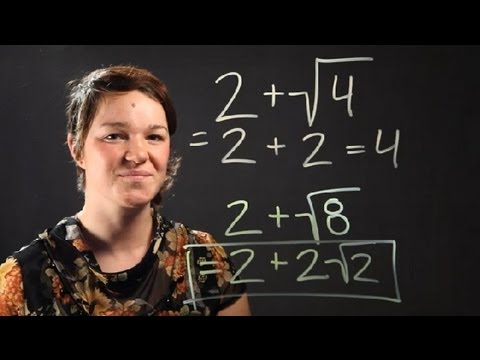Topic can you add two square roots: Can you add two square roots? Yes, you can, but only under certain conditions. This guide will help you understand when and how you can add square roots, providing clear examples and practical tips to make the process easy. Dive in to learn everything you need to know about adding square roots effectively.
Table of Content
- Adding Two Square Roots
- Introduction to Adding Square Roots
- Basic Principles of Square Roots
- Conditions for Adding Square Roots
- Direct Addition of Square Roots with Same Radicand
- Examples of Adding Identical Square Roots
- Simplifying Square Roots Before Addition
- Methods for Simplifying Square Roots
- Examples of Simplifying and Adding Square Roots
- Common Mistakes and Misconceptions
- Non-Additive Square Roots
- Advanced Techniques for Square Root Addition
- Applications of Adding Square Roots in Real Life
- Practice Problems and Solutions
- Conclusion and Key Takeaways
- YOUTUBE: Hướng dẫn thêm hai căn bậc hai bằng cách đơn giản hóa. Video này sẽ giúp bạn hiểu cách thêm các căn bậc hai thông qua các ví dụ minh họa.
Adding Two Square Roots
Adding two square roots involves understanding the properties of radicals. In general, square roots can be added directly only if they have the same radicand (the number inside the square root).
Basic Rule
The basic rule for adding square roots is:
\[\sqrt{a} + \sqrt{a} = 2\sqrt{a}\]
However, if the radicands are different, the square roots cannot be added directly:
\[\sqrt{a} + \sqrt{b} \neq \sqrt{a + b}\]
Example
Consider the following examples to understand the addition of square roots:
- \(\sqrt{3} + \sqrt{3} = 2\sqrt{3}\)
- \(\sqrt{5} + \sqrt{5} = 2\sqrt{5}\)
- \(\sqrt{7} + \sqrt{11}\) cannot be simplified further because the radicands are different.
Simplifying Square Roots
Sometimes, square roots can be simplified before adding them. For instance:
\[\sqrt{12} + \sqrt{27}\]
First, simplify the square roots:
\[\sqrt{12} = \sqrt{4 \cdot 3} = 2\sqrt{3}\]
\[\sqrt{27} = \sqrt{9 \cdot 3} = 3\sqrt{3}\]
Now, add the simplified square roots:
\[2\sqrt{3} + 3\sqrt{3} = (2 + 3)\sqrt{3} = 5\sqrt{3}\]
Table of Simplified Square Roots
| Expression | Simplified Form | Result |
|---|---|---|
| \(\sqrt{8} + \sqrt{18}\) | \(2\sqrt{2} + 3\sqrt{2}\) | 5\(\sqrt{2}\) |
| \(\sqrt{50} + \sqrt{32}\) | \(5\sqrt{2} + 4\sqrt{2}\) | 9\(\sqrt{2}\) |
| \(\sqrt{45} + \sqrt{20}\) | \(3\sqrt{5} + 2\sqrt{5}\) | 5\(\sqrt{5}\) |
Conclusion
Adding square roots is straightforward when the radicands are the same. If not, try simplifying the square roots first. If simplification is not possible, the square roots cannot be added directly.

READ MORE:
Introduction to Adding Square Roots
Adding square roots can be straightforward when you understand the underlying principles and rules. Square roots, denoted as \(\sqrt{}\), represent a value that, when multiplied by itself, gives the original number. Here's a step-by-step guide to help you add square roots effectively:
- Identical Radicands: Square roots can be added directly if the radicands (numbers under the square root sign) are the same.
- Different Radicands: If the radicands are different, square roots cannot be added directly.
- Simplifying Square Roots: Sometimes, simplifying square roots can make it possible to add them.
For example:
\[\sqrt{a} + \sqrt{a} = 2\sqrt{a}\]
For example:
\[\sqrt{a} + \sqrt{b} \neq \sqrt{a + b}\]
For instance:
\[\sqrt{12} + \sqrt{27}\]
First, simplify the square roots:
\[\sqrt{12} = \sqrt{4 \cdot 3} = 2\sqrt{3}\]
\[\sqrt{27} = \sqrt{9 \cdot 3} = 3\sqrt{3}\]
Now, add the simplified square roots:
\[2\sqrt{3} + 3\sqrt{3} = (2 + 3)\sqrt{3} = 5\sqrt{3}\]
By following these principles, you can confidently add square roots, whether they have identical or different radicands. Simplification is a key step when dealing with different radicands to see if they can be made identical for addition.
Basic Principles of Square Roots
Understanding the basic principles of square roots is essential for effectively performing operations involving them. Here are the key concepts to grasp:
- Definition of a Square Root: The square root of a number \(a\) is a value \(x\) such that \(x^2 = a\). It is denoted as \(\sqrt{a}\).
- Positive and Negative Roots: Every positive number has two square roots: a positive and a negative root.
- Properties of Square Roots: Square roots have several important properties that can be used to simplify expressions.
- Product Property: The square root of a product is the product of the square roots.
- Quotient Property: The square root of a quotient is the quotient of the square roots.
- Power Property: The square root of a number raised to a power can be simplified using fractional exponents.
- Rationalizing the Denominator: When square roots appear in the denominator of a fraction, rationalize by multiplying the numerator and the denominator by a suitable value.
For example:
\(\sqrt{16} = 4\) because \(4^2 = 16\).
For example:
\(\sqrt{9} = 3\) and \(-\sqrt{9} = -3\) because both \(3^2 = 9\) and \((-3)^2 = 9\).
\[\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\]
\[\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\]
\[\sqrt{a^2} = a\]
More generally, \(\sqrt{a^b} = a^{\frac{b}{2}}\).
For example:
\[\frac{1}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}\]
By mastering these basic principles, you will be well-prepared to handle more complex operations involving square roots, including addition, subtraction, multiplication, and division.
Conditions for Adding Square Roots
Adding square roots is a mathematical operation that requires specific conditions to be met. Understanding these conditions is crucial for correctly performing the addition. Here are the detailed conditions for adding square roots:
- Same Radicand: Square roots can only be added directly if they have the same radicand (the number inside the square root). This is similar to adding like terms in algebra.
- Simplification of Radicands: If the radicands are different, check if they can be simplified to the same radicand.
- Inability to Simplify: If the radicands cannot be simplified to the same value, the square roots cannot be added directly.
- Rational Numbers: In some cases, square roots involve rational numbers that can be factored out before performing the addition.
- Mixed Terms: When dealing with mixed terms involving square roots and integers, handle the square roots separately from the integers.
For example:
\(\sqrt{5} + \sqrt{5} = 2\sqrt{5}\)
However:
\(\sqrt{5} + \sqrt{3} \neq \sqrt{8}\)
For instance:
\(\sqrt{50} + \sqrt{18}\)
Simplify the square roots:
\(\sqrt{50} = \sqrt{25 \cdot 2} = 5\sqrt{2}\)
\(\sqrt{18} = \sqrt{9 \cdot 2} = 3\sqrt{2}\)
Now, add the simplified square roots:
\(5\sqrt{2} + 3\sqrt{2} = (5 + 3)\sqrt{2} = 8\sqrt{2}\)
For example:
\(\sqrt{7} + \sqrt{3}\) cannot be simplified or added directly.
For example:
\(2\sqrt{3} + 4\sqrt{3} = (2 + 4)\sqrt{3} = 6\sqrt{3}\)
For example:
\(2 + \sqrt{5} + 3 + \sqrt{5} = (2 + 3) + (\sqrt{5} + \sqrt{5}) = 5 + 2\sqrt{5}\)
By following these conditions, you can accurately add square roots and avoid common mistakes. Always look to simplify where possible, and remember that like terms are key to successful addition.
Direct Addition of Square Roots with Same Radicand
When adding square roots with the same radicand, the process is straightforward. This is because the square roots act like like terms in algebra. Here's a step-by-step guide to adding square roots with the same radicand:
- Identify the Radicand: Ensure that the square roots you are adding have the same radicand.
- Combine the Coefficients: If the radicands are the same, combine their coefficients (the numbers in front of the square root).
- Simplify the Expression: The combined expression is simplified by performing the addition of the coefficients.
- Multiple Terms: For multiple terms, follow the same rule for each pair of like terms.
For example:
\(\sqrt{a} + \sqrt{a}\)
For instance:
\(2\sqrt{5} + 3\sqrt{5} = (2 + 3)\sqrt{5} = 5\sqrt{5}\)
For example:
\(\sqrt{7} + \sqrt{7} = 1\sqrt{7} + 1\sqrt{7} = (1 + 1)\sqrt{7} = 2\sqrt{7}\)
For instance:
\(4\sqrt{3} + \sqrt{3} + 2\sqrt{3} = (4 + 1 + 2)\sqrt{3} = 7\sqrt{3}\)
Here's a table illustrating some examples:
| Expression | Step-by-Step | Result |
|---|---|---|
| \(\sqrt{2} + \sqrt{2}\) | \(1\sqrt{2} + 1\sqrt{2} = (1 + 1)\sqrt{2}\) | \(2\sqrt{2}\) |
| \(3\sqrt{5} + 4\sqrt{5}\) | \(3\sqrt{5} + 4\sqrt{5} = (3 + 4)\sqrt{5}\) | \(7\sqrt{5}\) |
| \(2\sqrt{10} + 5\sqrt{10}\) | \(2\sqrt{10} + 5\sqrt{10} = (2 + 5)\sqrt{10}\) | \(7\sqrt{10}\) |
By following these steps, you can easily add square roots with the same radicand, simplifying your expressions accurately and efficiently.
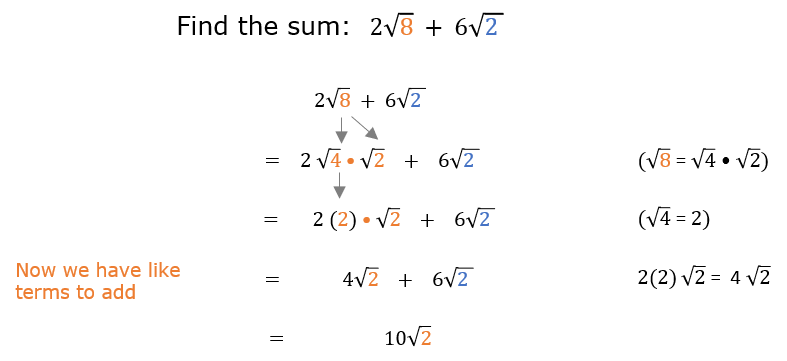
Examples of Adding Identical Square Roots
Adding identical square roots involves combining the coefficients of the square roots while keeping the radicand unchanged. Here are some detailed examples to illustrate this process:
- Basic Example:
- Example with Larger Coefficients:
- Example with Mixed Terms:
- Combining Multiple Identical Square Roots:
- Complex Example with Multiple Steps:
Consider the addition of two identical square roots:
\(\sqrt{3} + \sqrt{3}\)
Since the radicand is the same, combine the coefficients:
\(1\sqrt{3} + 1\sqrt{3} = (1 + 1)\sqrt{3} = 2\sqrt{3}\)
Adding square roots with coefficients:
\(4\sqrt{7} + 5\sqrt{7}\)
Combine the coefficients:
\(4\sqrt{7} + 5\sqrt{7} = (4 + 5)\sqrt{7} = 9\sqrt{7}\)
Adding more terms with the same radicand:
\(2\sqrt{5} + 3\sqrt{5} + \sqrt{5}\)
Combine the coefficients:
\(2\sqrt{5} + 3\sqrt{5} + 1\sqrt{5} = (2 + 3 + 1)\sqrt{5} = 6\sqrt{5}\)
Adding multiple identical square roots:
\(7\sqrt{2} + 2\sqrt{2} + 5\sqrt{2}\)
Combine the coefficients:
\(7\sqrt{2} + 2\sqrt{2} + 5\sqrt{2} = (7 + 2 + 5)\sqrt{2} = 14\sqrt{2}\)
Consider a more complex addition:
\(3\sqrt{11} + 2\sqrt{11} + 4\sqrt{11} + 6\sqrt{11}\)
Combine the coefficients:
\(3\sqrt{11} + 2\sqrt{11} + 4\sqrt{11} + 6\sqrt{11} = (3 + 2 + 4 + 6)\sqrt{11} = 15\sqrt{11}\)
These examples demonstrate that as long as the square roots have the same radicand, you can add them by simply combining their coefficients. This process helps simplify expressions and makes working with square roots more manageable.
Simplifying Square Roots Before Addition
Simplifying square roots before adding them is an essential step to ensure accuracy and ease in calculations. Here’s a detailed, step-by-step guide on how to simplify square roots before addition:
- Identify the Radicands:
- Factor the Radicands:
- Simplify the Expressions:
- Add the Simplified Square Roots:
- Handle Complex Expressions:
Look at the numbers under the square root sign and determine if they can be factored into simpler components.
For example:
\(\sqrt{18}\) and \(\sqrt{32}\)
Break down each radicand into its prime factors or factor pairs, preferably focusing on perfect squares.
For example:
\(\sqrt{18} = \sqrt{9 \cdot 2} = \sqrt{9} \cdot \sqrt{2} = 3\sqrt{2}\)
\(\sqrt{32} = \sqrt{16 \cdot 2} = \sqrt{16} \cdot \sqrt{2} = 4\sqrt{2}\)
Convert the square roots into their simplified forms.
For example:
\(\sqrt{18} = 3\sqrt{2}\)
\(\sqrt{32} = 4\sqrt{2}\)
Now that the square roots have the same radicand, add them by combining their coefficients.
For example:
\(3\sqrt{2} + 4\sqrt{2} = (3 + 4)\sqrt{2} = 7\sqrt{2}\)
For more complex expressions, simplify each term first and then combine.
For example:
\(\sqrt{50} + \sqrt{72}\)
Factor the radicands:
\(\sqrt{50} = \sqrt{25 \cdot 2} = 5\sqrt{2}\)
\(\sqrt{72} = \sqrt{36 \cdot 2} = 6\sqrt{2}\)
Add the simplified forms:
\(5\sqrt{2} + 6\sqrt{2} = (5 + 6)\sqrt{2} = 11\sqrt{2}\)
Here's a table summarizing the process with examples:
| Original Expression | Factorization | Simplified Form | Addition |
|---|---|---|---|
| \(\sqrt{18} + \sqrt{32}\) | \(\sqrt{9 \cdot 2} + \sqrt{16 \cdot 2}\) | \(3\sqrt{2} + 4\sqrt{2}\) | \((3 + 4)\sqrt{2} = 7\sqrt{2}\) |
| \(\sqrt{50} + \sqrt{72}\) | \(\sqrt{25 \cdot 2} + \sqrt{36 \cdot 2}\) | \(5\sqrt{2} + 6\sqrt{2}\) | \((5 + 6)\sqrt{2} = 11\sqrt{2}\) |
By simplifying square roots before addition, you ensure the process is efficient and error-free, leading to the correct results.
Methods for Simplifying Square Roots
Simplifying square roots is a fundamental skill in mathematics that makes calculations easier and more manageable. Here are detailed methods for simplifying square roots:
- Factorize the Radicand:
- Separate Perfect Squares:
- Apply the Square Root:
- Simplify the Expression:
- Use Prime Factorization:
- Common Factor Method:
Identify the prime factors or factor pairs of the number inside the square root (the radicand). Look for perfect squares within these factors.
For example:
\(\sqrt{72}\)
Factorize 72 into its prime factors: \(72 = 2^3 \cdot 3^2\).
Split the factors into perfect squares and other factors.
For example:
\(72 = 36 \cdot 2 = (6^2) \cdot 2\)
Take the square root of the perfect square and move it outside the radical sign.
For example:
\(\sqrt{72} = \sqrt{36 \cdot 2} = \sqrt{36} \cdot \sqrt{2} = 6\sqrt{2}\)
Combine the simplified factors to express the square root in its simplest form.
For example:
\(\sqrt{72} = 6\sqrt{2}\)
For more complex numbers, use prime factorization to simplify.
For example:
\(\sqrt{180}\)
Prime factorization: \(180 = 2^2 \cdot 3^2 \cdot 5\)
Separate the perfect squares:
\(180 = (2^2 \cdot 3^2) \cdot 5 = 36 \cdot 5\)
Apply the square root:
\(\sqrt{180} = \sqrt{36 \cdot 5} = \sqrt{36} \cdot \sqrt{5} = 6\sqrt{5}\)
Use the common factor method to simplify expressions with multiple terms.
For example:
\(\sqrt{50} + \sqrt{8}\)
Factorize the radicands:
\(\sqrt{50} = \sqrt{25 \cdot 2} = 5\sqrt{2}\)
\(\sqrt{8} = \sqrt{4 \cdot 2} = 2\sqrt{2}\)
Now, the expression can be combined as:
\(5\sqrt{2} + 2\sqrt{2} = (5 + 2)\sqrt{2} = 7\sqrt{2}\)
Here's a table summarizing these methods with examples:
| Original Expression | Factorization | Simplified Form |
|---|---|---|
| \(\sqrt{72}\) | \(72 = 36 \cdot 2\) | \(6\sqrt{2}\) |
| \(\sqrt{180}\) | \(180 = 36 \cdot 5\) | \(6\sqrt{5}\) |
| \(\sqrt{50} + \sqrt{8}\) | \(\sqrt{25 \cdot 2} + \sqrt{4 \cdot 2}\) | \(5\sqrt{2} + 2\sqrt{2} = 7\sqrt{2}\) |
By using these methods, you can simplify square roots efficiently, making addition and other operations easier to perform.
Examples of Simplifying and Adding Square Roots
Adding square roots can be straightforward if the radicands (the numbers under the square root) are the same. If the radicands are different, we need to simplify the square roots before adding. Here are some detailed examples to illustrate this process:
Example 1: Adding Square Roots with the Same Radicand
Consider the following expression:
\(\sqrt{5} + 3\sqrt{5}\)
Since both terms have the same radicand (5), we can directly add them:
\(\sqrt{5} + 3\sqrt{5} = 4\sqrt{5}\)
Example 2: Simplifying Before Adding
Let's add \(\sqrt{50}\) and \(\sqrt{18}\). These do not have the same radicand, so we need to simplify each square root first.
- Simplify \(\sqrt{50}\):
- Prime factorize 50: \(50 = 2 \times 5^2\)
- \(\sqrt{50} = \sqrt{2 \times 5^2} = 5\sqrt{2}\)
- Simplify \(\sqrt{18}\):
- Prime factorize 18: \(18 = 2 \times 3^2\)
- \(\sqrt{18} = \sqrt{2 \times 3^2} = 3\sqrt{2}\)
- Now add the simplified square roots:
- \(5\sqrt{2} + 3\sqrt{2} = (5 + 3)\sqrt{2} = 8\sqrt{2}\)
Example 3: Simplifying to Create Like Radicands
Consider the expression: \(2\sqrt{8} + 3\sqrt{2}\). First, simplify \(\sqrt{8}\).
- Simplify \(\sqrt{8}\):
- Prime factorize 8: \(8 = 2^3\)
- \(\sqrt{8} = \sqrt{2^3} = 2\sqrt{2}\)
- Now rewrite the expression using the simplified form:
- \(2\sqrt{8} = 2 \times 2\sqrt{2} = 4\sqrt{2}\)
- The expression becomes \(4\sqrt{2} + 3\sqrt{2}\)
- Now add the like terms:
- \(4\sqrt{2} + 3\sqrt{2} = (4 + 3)\sqrt{2} = 7\sqrt{2}\)
Example 4: Complex Example with Coefficients
Let's add \(3\sqrt{12} + 2\sqrt{27}\). We start by simplifying each square root.
- Simplify \(\sqrt{12}\):
- Prime factorize 12: \(12 = 2^2 \times 3\)
- \(\sqrt{12} = \sqrt{2^2 \times 3} = 2\sqrt{3}\)
- The term becomes \(3 \times 2\sqrt{3} = 6\sqrt{3}\)
- Simplify \(\sqrt{27}\):
- Prime factorize 27: \(27 = 3^3\)
- \(\sqrt{27} = \sqrt{3^3} = 3\sqrt{3}\)
- The term becomes \(2 \times 3\sqrt{3} = 6\sqrt{3}\)
- Now add the simplified terms:
- \(6\sqrt{3} + 6\sqrt{3} = (6 + 6)\sqrt{3} = 12\sqrt{3}\)
By following these steps, you can successfully simplify and add square roots. Remember, the key is to ensure that the square roots have the same radicand before combining them.

Common Mistakes and Misconceptions
When adding square roots, it is crucial to avoid common mistakes and misconceptions. Below are some key points to consider:
1. Adding Radicals with Different Radicands
A common error is trying to add square roots with different radicands directly. For example:
- \(\sqrt{2} + \sqrt{3} \neq \sqrt{5}\)
Square roots can only be added directly if they have the same radicand. For instance:
- \(2\sqrt{5} + 3\sqrt{5} = 5\sqrt{5}\)
2. Simplification Before Addition
Before adding, ensure that all square roots are simplified. For example:
- \(\sqrt{8} + \sqrt{2} = 2\sqrt{2} + \sqrt{2} = 3\sqrt{2}\)
3. Misinterpreting Coefficients
When adding square roots with coefficients, only the coefficients of like radicals should be added. For instance:
- \(4\sqrt{7} + 3\sqrt{7} = 7\sqrt{7}\)
However, different radicals remain unchanged:
- \(3\sqrt{2} + 2\sqrt{3} = 3\sqrt{2} + 2\sqrt{3}\)
4. Incorrect Subtraction of Radicals
Similar to addition, only like radicals can be subtracted:
- \(5\sqrt{11} - 2\sqrt{11} = 3\sqrt{11}\)
Radicals with different radicands cannot be subtracted directly:
- \(\sqrt{5} - \sqrt{3} \neq \sqrt{2}\)
5. Misapplying Product Property
Another common mistake is incorrectly applying the product property of square roots. For example:
- \(\sqrt{a} \cdot \sqrt{b} = \sqrt{ab}\)
- \(\sqrt{2} \cdot \sqrt{8} = \sqrt{16} = 4\)
Ensure the correct application of properties to avoid errors.
6. Neglecting Simplification of Square Roots
Always simplify square roots before performing operations:
- \(\sqrt{18} + 6\sqrt{2} = 3\sqrt{2} + 6\sqrt{2} = 9\sqrt{2}\)
Examples to Avoid
- Incorrect: \(\sqrt{12} + \sqrt{27} = \sqrt{39}\)
- Correct: \(\sqrt{12} + \sqrt{27} = 2\sqrt{3} + 3\sqrt{3} = 5\sqrt{3}\)
By understanding these common mistakes and misconceptions, you can accurately add square roots and avoid errors in your calculations.
Non-Additive Square Roots
Square roots cannot always be added together. The rules for adding square roots are quite specific, and failing to adhere to them is a common mistake. Below, we discuss the conditions under which square roots are non-additive and provide examples to illustrate these scenarios.
Generally, square roots can only be added if they have the same radicand. The radicand is the number under the square root symbol. Here are some detailed examples and explanations:
- Different Radicands:
Consider the expression:
\(\sqrt{2} + \sqrt{3}\)
Since the radicands (2 and 3) are different, these square roots cannot be added directly. The expression remains:
\(\sqrt{2} + \sqrt{3}\)
- Simplifying Radicals:
Sometimes, the radicands appear different but can be simplified to a common value. However, if simplification does not lead to the same radicand, addition is still not possible.
Example:
\(\sqrt{8} + \sqrt{18}\)
Simplify each square root:
- \(\sqrt{8} = \sqrt{4 \times 2} = 2\sqrt{2}\)
- \(\sqrt{18} = \sqrt{9 \times 2} = 3\sqrt{2}\)
Now the expression is:
\(2\sqrt{2} + 3\sqrt{2} = 5\sqrt{2}\)
If the radicals had simplified to different values, they would remain non-additive.
- Square Roots with Coefficients:
When square roots have coefficients, the rule of common radicands still applies.
Example:
\(4\sqrt{5} + 3\sqrt{7}\)
Since 5 and 7 are different radicands, the expression cannot be simplified further:
\(4\sqrt{5} + 3\sqrt{7}\)
- Misconceptions:
- Assuming that any square roots can be added if they are both under a square root sign.
- Forgetting to simplify the square roots first before checking for common radicands.
In conclusion, always check the radicands before attempting to add square roots. Only like terms, with the same radicand, can be added directly. Otherwise, the expression remains as it is.
Advanced Techniques for Square Root Addition
When adding square roots, especially those with coefficients or complex expressions, employing advanced techniques can simplify the process and improve accuracy. Below are some detailed methods to tackle advanced square root addition:
1. Simplifying Each Radical
Start by simplifying each square root to its simplest form. This involves factoring the radicand into its prime factors and extracting pairs of primes:
- For example, simplify \(\sqrt{50}\):
- Factorize 50 into \(25 \times 2\).
- \(\sqrt{50} = \sqrt{25 \times 2} = 5\sqrt{2}\).
- Simplify \(\sqrt{72}\):
- Factorize 72 into \(36 \times 2\).
- \(\sqrt{72} = \sqrt{36 \times 2} = 6\sqrt{2}\).
2. Identifying Like Radicals
Like radicals have the same radicand. When adding square roots, ensure they have the same radicand before combining:
- \(\sqrt{50} = 5\sqrt{2}\) and \(\sqrt{72} = 6\sqrt{2}\) can be combined because they both contain \(\sqrt{2}\).
- Combine them: \(5\sqrt{2} + 6\sqrt{2} = 11\sqrt{2}\).
3. Using Rationalization
For expressions involving square roots in the denominator, rationalizing the denominator is crucial:
- Example: \(\frac{1}{\sqrt{2}} + \frac{1}{\sqrt{3}}\)
- Rationalize each term:
- \(\frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}\)
- \(\frac{1}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{\sqrt{3}}{3}\)
- Combine the rationalized terms: \(\frac{\sqrt{2}}{2} + \frac{\sqrt{3}}{3}\)
4. Applying the Distributive Property
Use the distributive property to simplify expressions before adding or subtracting:
- Example: \(2\sqrt{3} + 4\sqrt{3} = (2 + 4)\sqrt{3} = 6\sqrt{3}\)
5. Combining Coefficients
For like radicals, simply add or subtract the coefficients while keeping the radicand unchanged:
- Example: \(7\sqrt{5} + 3\sqrt{5} = 10\sqrt{5}\)
- Example: \(8\sqrt{7} - 2\sqrt{7} = 6\sqrt{7}\)
6. Using Conjugates for Complex Denominators
When dealing with binomials that include square roots, multiply by the conjugate to simplify:
- Example: \(\frac{1}{1+\sqrt{2}} \times \frac{1-\sqrt{2}}{1-\sqrt{2}} = \frac{1-\sqrt{2}}{1-2} = \frac{1-\sqrt{2}}{-1} = -1 + \sqrt{2}\)
7. Practice Problems
- Simplify and add: \(\sqrt{18} + \sqrt{8}\)
- Simplify: \(\sqrt{18} = 3\sqrt{2}\), \(\sqrt{8} = 2\sqrt{2}\)
- Add: \(3\sqrt{2} + 2\sqrt{2} = 5\sqrt{2}\)
- Simplify and add: \(2\sqrt{75} + 3\sqrt{3}\)
- Simplify: \(2\sqrt{75} = 10\sqrt{3}\), \(\sqrt{27} = 3\sqrt{3}\)
- Add: \(10\sqrt{3} + 3\sqrt{3} = 13\sqrt{3}\)
By mastering these advanced techniques, you can handle complex square root addition with greater confidence and precision.
Applications of Adding Square Roots in Real Life
Square roots and their addition play a significant role in various real-life applications. Here are some examples:
-
1. Architecture and Engineering
Square roots are used to calculate dimensions and structural integrity. For example, determining the diagonal length of a rectangular component uses the Pythagorean theorem, which involves square roots:
\( \text{Diagonal} = \sqrt{a^2 + b^2} \)
Adding square roots helps in calculating combined lengths or areas of different components accurately.
-
2. Finance
In finance, square roots are used to calculate stock market volatility, which measures the variability of stock prices. The formula involves the square root of the variance of stock returns:
\( \text{Volatility} = \sqrt{\text{Variance}} \)
Investors use these calculations to assess risk and make informed investment decisions.
-
3. Navigation
Square roots are crucial in navigation for calculating distances between points. The distance formula in 2D and 3D space involves square roots:
2D: \( D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
3D: \( D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2} \)
Adding these distances can help in plotting accurate routes and travel plans.
-
4. Computer Science
In computer graphics, square roots are used to compute the distance between pixels or vertices, crucial for rendering images and animations. For example, in calculating the Euclidean distance between two points:
\( \text{Distance} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
Adding these distances helps in developing realistic graphics and simulations.
-
5. Science
Square roots are used in various scientific calculations, such as determining the speed of an object or the intensity of sound waves. For example, in physics, the kinetic energy (KE) formula involves square roots:
\( \text{KE} = \frac{1}{2}mv^2 \)
Adding square roots is essential for combining different energy values or wave intensities.
These examples highlight the diverse applications of adding square roots in real-life scenarios, showcasing their importance in various fields such as architecture, finance, navigation, computer science, and science.
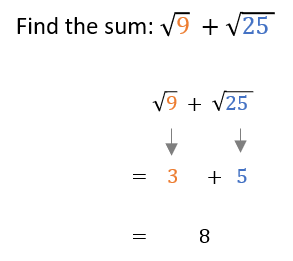
Practice Problems and Solutions
Below are a series of practice problems designed to help you master the addition of square roots. Each problem is followed by a step-by-step solution.
-
Simplify and add: \( 3\sqrt{5} + 6\sqrt{5} \)
- \(\text{Step 1: Identify the common radicand:} \ \sqrt{5}\)
- \(\text{Step 2: Add the coefficients:} \ 3 + 6 = 9\)
- \(\text{Solution:} \ 3\sqrt{5} + 6\sqrt{5} = 9\sqrt{5} \)
-
Simplify and subtract: \( 7\sqrt{3} - 3\sqrt{3} \)
- \(\text{Step 1: Identify the common radicand:} \ \sqrt{3}\)
- \(\text{Step 2: Subtract the coefficients:} \ 7 - 3 = 4\)
- \(\text{Solution:} \ 7\sqrt{3} - 3\sqrt{3} = 4\sqrt{3} \)
-
Simplify and add: \( 5\sqrt{7} + 6\sqrt{7} \)
- \(\text{Step 1: Identify the common radicand:} \ \sqrt{7}\)
- \(\text{Step 2: Add the coefficients:} \ 5 + 6 = 11\)
- \(\text{Solution:} \ 5\sqrt{7} + 6\sqrt{7} = 11\sqrt{7} \)
-
Simplify and add: \( \sqrt{3} + 4\sqrt{3} \)
- \(\text{Step 1: Identify the common radicand:} \ \sqrt{3}\)
- \(\text{Step 2: Add the coefficients:} \ 1 + 4 = 5\)
- \(\text{Solution:} \ \sqrt{3} + 4\sqrt{3} = 5\sqrt{3} \)
-
Simplify and add: \( 2\sqrt{5} + 3\sqrt{5} + 4\sqrt{5} \)
- \(\text{Step 1: Identify the common radicand:} \ \sqrt{5}\)
- \(\text{Step 2: Add the coefficients:} \ 2 + 3 + 4 = 9\)
- \(\text{Solution:} \ 2\sqrt{5} + 3\sqrt{5} + 4\sqrt{5} = 9\sqrt{5} \)
-
Simplify and add: \( 3\sqrt{2} + 5\sqrt{5} + 8\sqrt{2} - 2\sqrt{5} \)
- \(\text{Step 1: Group like terms:} \ 3\sqrt{2} + 8\sqrt{2} \text{ and } 5\sqrt{5} - 2\sqrt{5}\)
- \(\text{Step 2: Add the coefficients of like terms:} \ (3 + 8)\sqrt{2} \text{ and } (5 - 2)\sqrt{5}\)
- \(\text{Step 3: Simplify:} \ 11\sqrt{2} + 3\sqrt{5}\)
- \(\text{Solution:} \ 3\sqrt{2} + 5\sqrt{5} + 8\sqrt{2} - 2\sqrt{5} = 11\sqrt{2} + 3\sqrt{5} \)
-
Simplify and add: \( 2\sqrt{12} + 5\sqrt{27} \)
- \(\text{Step 1: Simplify each term:} \ 2\sqrt{12} = 2\sqrt{4 \cdot 3} = 2 \cdot 2\sqrt{3} = 4\sqrt{3}\)
- \(\text{Step 2: Simplify each term:} \ 5\sqrt{27} = 5\sqrt{9 \cdot 3} = 5 \cdot 3\sqrt{3} = 15\sqrt{3}\)
- \(\text{Step 3: Add the simplified terms:} \ 4\sqrt{3} + 15\sqrt{3} = 19\sqrt{3}\)
- \(\text{Solution:} \ 2\sqrt{12} + 5\sqrt{27} = 19\sqrt{3} \)
Conclusion and Key Takeaways
In this section, we summarize the essential points about adding square roots and reflect on the key concepts discussed throughout the article.
- Understanding Radicands: To add square roots effectively, it is crucial to recognize and work with like radicands. Square roots with different radicands cannot be directly combined.
- Simplification: Always simplify square roots as much as possible before attempting addition. This process can often reveal like radicands, allowing for combination.
- Identical Square Roots: When dealing with identical square roots, simply add the coefficients. For example, \(2\sqrt{5} + 3\sqrt{5} = 5\sqrt{5}\).
- Complex Expressions: In more complex cases, use advanced techniques such as rationalizing and simplifying expressions under the radical to facilitate addition.
- Real-Life Applications: Adding square roots is not just a mathematical exercise; it has practical applications in fields like engineering, physics, and finance, where precise calculations are necessary.
In conclusion, mastering the addition of square roots involves understanding when and how to simplify and combine them. Recognizing like radicands and applying proper mathematical rules ensures accurate results. Keep practicing with various problems to reinforce these skills and apply them effectively in both academic and real-world scenarios.
Hướng dẫn thêm hai căn bậc hai bằng cách đơn giản hóa. Video này sẽ giúp bạn hiểu cách thêm các căn bậc hai thông qua các ví dụ minh họa.
Thêm hai căn bậc hai bằng cách đơn giản hóa
READ MORE:
Hướng dẫn cách cộng và trừ căn bậc hai. Video này sẽ giúp bạn nắm vững các nguyên tắc cơ bản và ứng dụng thực tế.
Cách Cộng và Trừ Căn Bậc Hai