Topic 1/square root 2: The expression 1/square root 2, often encountered in mathematics, simplifies to square root 2 over 2. This simplification is crucial in various fields, including algebra and geometry. Understanding this concept can aid in solving complex mathematical problems and enhancing comprehension of radical expressions.
Table of Content
- Simplifying \( \frac{1}{\sqrt{2}} \)
- Introduction to 1/Square Root of 2
- Simplification of 1/Square Root of 2
- Decimal Value of 1/Square Root of 2
- Mathematical Properties
- Historical Significance
- Applications of 1/Square Root of 2
- Methods to Calculate Square Root of 2
- Common Questions
- Examples and Practice Problems
- YOUTUBE:
Simplifying \( \frac{1}{\sqrt{2}} \)
The expression \( \frac{1}{\sqrt{2}} \) can be simplified by rationalizing the denominator. This involves multiplying both the numerator and the denominator by \( \sqrt{2} \), which removes the square root from the denominator.
Steps to Simplify \( \frac{1}{\sqrt{2}} \)
- Start with the expression: \( \frac{1}{\sqrt{2}} \).
- Multiply the numerator and the denominator by \( \sqrt{2} \):
\[ \frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2} \]
The simplified form of \( \frac{1}{\sqrt{2}} \) is \( \frac{\sqrt{2}}{2} \).
Decimal Approximation
The decimal approximation of \( \frac{\sqrt{2}}{2} \) is approximately 0.7071, given that \( \sqrt{2} \approx 1.4142 \).
Applications and Historical Context
The square root of 2 (\( \sqrt{2} \)) has significant historical importance and applications in various fields, including geometry and architecture. It is an irrational number, meaning it cannot be expressed as a simple fraction. The approximation \( \frac{99}{70} \) is sometimes used for practical calculations, though it is slightly less accurate than more refined approximations.
In ancient Roman architecture, the concept of \( \sqrt{2} \) was used to design square-based structures, ensuring proportional accuracy in the layout of floors and pavements.
Interesting Fact
The discovery that \( \sqrt{2} \) is irrational is often attributed to the ancient Greek mathematician Hippasus of Metapontum, who was associated with the Pythagorean school. According to legend, the Pythagoreans initially kept this discovery a secret because it challenged their belief that all numbers could be expressed as the ratio of integers.
Conclusion
Understanding how to simplify \( \frac{1}{\sqrt{2}} \) is a fundamental skill in algebra that extends to various mathematical and practical applications. This simplification highlights the importance of rationalizing denominators to facilitate further calculations.

READ MORE:
Introduction to 1/Square Root of 2
The fraction \( \frac{1}{\sqrt{2}} \) is commonly encountered in mathematics, particularly in algebra and trigonometry. This expression often arises in problems involving right triangles, especially those related to the 45°-45°-90° triangle, where the legs are equal and the hypotenuse is \( \sqrt{2} \) times the length of a leg. Simplifying \( \frac{1}{\sqrt{2}} \) involves rationalizing the denominator, which makes the expression easier to use in further calculations.
Steps to Simplify \( \frac{1}{\sqrt{2}} \)
- Multiply the numerator and the denominator by \( \sqrt{2} \):
\[
\frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}
\] - Combine and simplify the expression to achieve a rational denominator:
\[
\frac{\sqrt{2}}{2}
\]
Rationalizing the Denominator
Rationalizing the denominator refers to the process of eliminating the radical from the denominator of a fraction. This is done by multiplying both the numerator and the denominator by a conjugate or an appropriate radical that results in a perfect square in the denominator. For \( \frac{1}{\sqrt{2}} \), multiplying by \( \sqrt{2} \) achieves this goal:
- Multiply \( \frac{1}{\sqrt{2}} \) by \( \frac{\sqrt{2}}{\sqrt{2}} \):
\[
\frac{1 \times \sqrt{2}}{\sqrt{2} \times \sqrt{2}} = \frac{\sqrt{2}}{2}
\]
Applications of \( \frac{1}{\sqrt{2}} \)
- In trigonometry, \( \sin 45^\circ \) and \( \cos 45^\circ \) are both equal to \( \frac{1}{\sqrt{2}} \), which is simplified to \( \frac{\sqrt{2}}{2} \).
- In physics, this value is used in wave functions and quantum mechanics.
- In engineering, \( \frac{1}{\sqrt{2}} \) is encountered in signal processing and other areas where trigonometric functions are used.
Decimal Representation
The decimal approximation of \( \frac{1}{\sqrt{2}} \) is approximately 0.7071. This value is useful in various computational applications where an exact fraction is less practical.
Simplification of 1/Square Root of 2
The expression \( \frac{1}{\sqrt{2}} \) can be simplified by rationalizing the denominator. This involves removing the square root from the denominator, which can be achieved by multiplying both the numerator and the denominator by \( \sqrt{2} \).
- Start with the expression \( \frac{1}{\sqrt{2}} \).
- Multiply both the numerator and the denominator by \( \sqrt{2} \):
\[ \frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2} \] - Combine and simplify the result:
\[ \frac{\sqrt{2}}{2} \]
Thus, the simplified form of \( \frac{1}{\sqrt{2}} \) is \( \frac{\sqrt{2}}{2} \). This is a common result in mathematics, often used in trigonometry and other areas where square roots are involved.
Decimal Value of 1/Square Root of 2
The value of \( \frac{1}{\sqrt{2}} \) in decimal form is approximately 0.7071067811865475. This value is derived from the fact that the square root of 2 is an irrational number, approximately equal to 1.414213562373095.
Steps to Derive the Decimal Value
- Identify the value of \( \sqrt{2} \), which is approximately 1.414213562373095.
- Calculate \( \frac{1}{\sqrt{2}} \):
- In fractional form: \( \frac{1}{1.414213562373095} \).
- Perform the division to get the decimal form, which is approximately 0.7071067811865475.
Accuracy and Precision
The value 0.7071067811865475 is a truncated version of the true decimal value of \( \frac{1}{\sqrt{2}} \). This value can be extended to more decimal places for higher precision. However, in most practical applications, the value 0.7071067811865475 is sufficiently accurate.
Table of Values
| Number of Decimal Places | Value |
|---|---|
| 5 | 0.70711 |
| 10 | 0.7071067812 |
| 15 | 0.707106781186548 |
In summary, \( \frac{1}{\sqrt{2}} \) is a significant mathematical constant with an approximate decimal value of 0.7071067811865475, used in various scientific and mathematical computations.
Mathematical Properties
The expression \( \frac{1}{\sqrt{2}} \) is rich in mathematical properties and applications. Below are some key properties and insights into this expression:
- Irrational Nature: The value of \( \sqrt{2} \) is known to be an irrational number. Consequently, \( \frac{1}{\sqrt{2}} \) is also irrational. This means it cannot be expressed as a fraction of two integers.
- Rationalization: To rationalize the denominator of \( \frac{1}{\sqrt{2}} \), we multiply the numerator and the denominator by \( \sqrt{2} \): \[ \frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2} \] This results in a simpler expression that is often easier to use in further calculations.
- Geometric Interpretation: In geometry, \( \frac{1}{\sqrt{2}} \) frequently appears as the length of the sides of a right triangle with legs of equal length (isosceles right triangle) where the hypotenuse is normalized to 1.
- Decimal Approximation: The decimal representation of \( \frac{1}{\sqrt{2}} \) is approximately 0.7071067811865475, which is useful for practical calculations where an exact representation is not required.
- Trigonometric Functions: The value \( \frac{1}{\sqrt{2}} \) is encountered in trigonometry, particularly as \( \sin(45^\circ) \) and \( \cos(45^\circ) \). These trigonometric functions are fundamental in various mathematical and physical applications.

Historical Significance
The mathematical constant \( \frac{1}{\sqrt{2}} \), often encountered in various fields of mathematics and science, holds significant historical importance.
The discovery of \( \sqrt{2} \) being an irrational number dates back to ancient Greece, where the Pythagoreans first recognized its incommensurability. This realization challenged their belief that all numbers could be expressed as ratios of integers, leading to significant developments in mathematical theory.
Babylonian mathematicians also showed remarkable understanding of \( \sqrt{2} \). A Babylonian clay tablet from around 1800 BCE (YBC 7289) contains a highly accurate approximation of \( \sqrt{2} \), demonstrating their advanced mathematical capabilities.
In the Renaissance period, mathematicians continued to explore the properties of \( \sqrt{2} \). For instance, the Indian mathematician Bhaskara I provided methods for approximating \( \sqrt{2} \) with considerable accuracy. The continued interest in this number reflected its importance in various mathematical contexts.
In modern times, the value of \( \sqrt{2} \) has been used extensively in the field of engineering and physics. The aspect ratio of the ISO 216 standard for paper sizes (such as A4) is based on \( \sqrt{2} \), ensuring that each paper size can be scaled up or down while preserving the same proportions. This practical application demonstrates the continued relevance of \( \sqrt{2} \) in everyday life.
Overall, \( \frac{1}{\sqrt{2}} \) and its associated mathematical constant \( \sqrt{2} \) have played a critical role throughout history, influencing various fields from theoretical mathematics to practical applications in science and engineering.
Applications of 1/Square Root of 2
The value \( \frac{1}{\sqrt{2}} \) has several practical applications across different fields of science and mathematics. Below are some key applications:
-
Geometry
In geometry, \( \frac{1}{\sqrt{2}} \) is significant in the context of right-angled triangles and squares. For example, in a square, the length of the diagonal can be calculated using this value. If the side length of a square is \( s \), the diagonal \( d \) is given by:
\[
d = s \sqrt{2}
\]Hence, the inverse can be represented as:
\[
s = d \cdot \frac{1}{\sqrt{2}}
\] -
Trigonometry
In trigonometry, \( \frac{1}{\sqrt{2}} \) corresponds to the sine and cosine of 45 degrees (or \( \pi/4 \) radians). Specifically,
\[
\sin 45^\circ = \cos 45^\circ = \frac{1}{\sqrt{2}}
\]This value is crucial in solving problems involving angles and in the simplification of trigonometric expressions.
-
Physics
In physics, \( \frac{1}{\sqrt{2}} \) appears in the normalization of wave functions in quantum mechanics. For example, in the quantum mechanical description of the hydrogen atom, the wave functions are normalized to ensure that the total probability density equals 1. This normalization often involves factors of \( \frac{1}{\sqrt{2}} \) in the equations.
-
Computer Graphics
In computer graphics, \( \frac{1}{\sqrt{2}} \) is used in algorithms for scaling and rotation transformations. For instance, rotating a vector by 45 degrees involves multiplying its components by \( \frac{1}{\sqrt{2}} \) to maintain the correct proportions.
-
Electrical Engineering
In electrical engineering, \( \frac{1}{\sqrt{2}} \) is used in the analysis of alternating current (AC) circuits. The root mean square (RMS) value of an AC signal, which is essential for calculating power, involves \( \frac{1}{\sqrt{2}} \) as part of its formula.
These applications illustrate the versatility and importance of \( \frac{1}{\sqrt{2}} \) in various scientific and mathematical domains, highlighting its role in simplifying and solving complex problems.
Methods to Calculate Square Root of 2
The square root of 2 (\( \sqrt{2} \)) can be calculated using several methods, each offering varying levels of precision and complexity. Here are some commonly used methods:
-
Estimation and Approximation Method:
This method involves iteratively improving the estimate of \( \sqrt{2} \). A simple formula used is:
\[
y_{n+1} = \frac{x / y_n + y_n}{2}
\]
where \( y_1 \) is an initial guess. For \( \sqrt{2} \), if we start with \( y_1 = 1 \), the iterations are:- Iteration 1: \( y_1 = \frac{2 + 1}{2} = 1.5 \)
- Iteration 2: \( y_2 = \frac{2 / 1.5 + 1.5}{2} \approx 1.4167 \)
- Iteration 3: \( y_3 = \frac{2 / 1.4167 + 1.4167}{2} \approx 1.4142 \)
Repeating this process yields a value closer to the true value of \( \sqrt{2} \) which is approximately 1.414213562373095.
-
Babylonian Method (Heron's Method):
This ancient method is a special case of the Newton-Raphson method and follows a similar iterative process:
\[
y_{n+1} = \frac{y_n + \frac{2}{y_n}}{2}
\]Starting with \( y_1 = 1 \), the iterations proceed similarly to the Estimation method, quickly converging to the value of \( \sqrt{2} \).
-
Long Division Method:
This manual method provides a step-by-step approach to finding the square root, similar to long division. Here’s a brief outline of the process:
- Set up the number in pairs of digits starting from the decimal point.
- Find the largest integer whose square is less than or equal to the first pair.
- Subtract the square of this integer from the first pair and bring down the next pair.
- Double the divisor and find a new digit for the quotient that, when added to the divisor and multiplied, gives a product less than or equal to the current dividend.
- Repeat the process to obtain more decimal places.
-
Newton's Method:
This powerful iterative method starts with an initial guess \( y_0 \) and refines it using the formula:
\[
y_{n+1} = y_n - \frac{f(y_n)}{f'(y_n)}
\]For \( \sqrt{2} \), \( f(y) = y^2 - 2 \) and \( f'(y) = 2y \), leading to:
\[
y_{n+1} = \frac{y_n + \frac{2}{y_n}}{2}
\]This is equivalent to the Babylonian method and converges very quickly to the accurate value.
Each method offers a different balance between simplicity and computational efficiency, allowing for the calculation of \( \sqrt{2} \) to the desired degree of accuracy.
Common Questions
-
Why is the square root of 2 an irrational number?
The square root of 2 is irrational because it cannot be expressed as a simple fraction. A common proof involves contradiction: assuming \( \sqrt{2} \) is rational leads to a logical contradiction, proving it must be irrational.
-
How to find the length of the diagonal of a square?
The length of the diagonal of a square can be found using the formula \( d = s \sqrt{2} \), where \( s \) is the side length of the square. For example, if the side length is 1, the diagonal is \( 1 \times \sqrt{2} = \sqrt{2} \).
-
What is the decimal approximation of \( \frac{1}{\sqrt{2}} \)?
The decimal approximation of \( \frac{1}{\sqrt{2}} \) is approximately 0.7071. This value is used in various calculations in geometry and trigonometry.
-
How is \( \frac{1}{\sqrt{2}} \) used in trigonometry?
In trigonometry, \( \frac{1}{\sqrt{2}} \) is commonly seen as the sine and cosine of 45 degrees (or \( \frac{\pi}{4} \) radians). It is crucial in deriving values for other trigonometric functions at these angles.
-
Can \( \frac{1}{\sqrt{2}} \) be simplified further?
Yes, \( \frac{1}{\sqrt{2}} \) can be simplified by rationalizing the denominator, resulting in \( \frac{\sqrt{2}}{2} \).
-
What are some methods to calculate the square root of 2?
Common methods include the Babylonian method (an iterative approximation), Newton's method (a refined iterative process), and using a calculator for a quick decimal approximation.

Examples and Practice Problems
Working with \( \frac{1}{\sqrt{2}} \) can be enhanced through various examples and practice problems. Below are detailed steps and problems to help solidify understanding.
Examples
- Example 1: Simplifying \( \frac{1}{\sqrt{2}} \)
- Start with the expression: \( \frac{1}{\sqrt{2}} \)
- Rationalize the denominator by multiplying the numerator and the denominator by \( \sqrt{2} \): \( \frac{1 \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}} \)
- Simplify the expression: \( \frac{\sqrt{2}}{2} \)
- Example 2: Using \( \frac{1}{\sqrt{2}} \) in Geometry
- Find the length of the diagonal of a square with side length 1.
- The diagonal \( d \) is given by \( d = s \sqrt{2} \), where \( s \) is the side length.
- Substitute \( s = 1 \): \( d = 1 \cdot \sqrt{2} = \sqrt{2} \)
- The value of \( \frac{1}{\sqrt{2}} \) is used to express the sine or cosine of \( 45^\circ \) as: \( \sin(45^\circ) = \cos(45^\circ) = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2} \)
Practice Problems
- Problem 1: Rationalize the following expression:
Rationalize \( \frac{3}{\sqrt{2}} \) and simplify.
- Multiply numerator and denominator by \( \sqrt{2} \): \( \frac{3 \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}} \)
- Simplify: \( \frac{3 \sqrt{2}}{2} \)
- Problem 2: Simplify the following expression involving square roots:
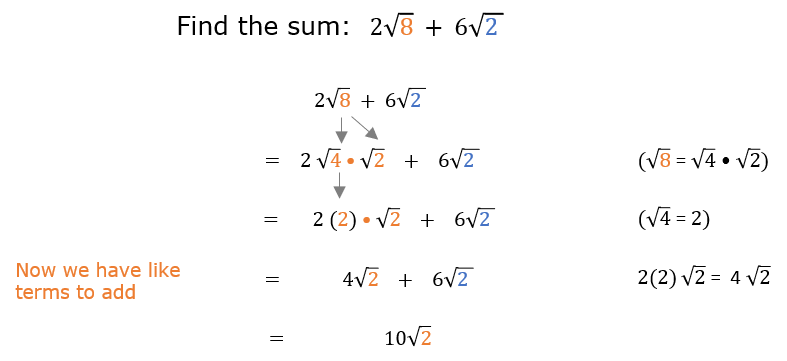
Simplify \( \frac{2}{\sqrt{8}} \).
- Rewrite the square root: \( \sqrt{8} = \sqrt{4 \cdot 2} = 2 \sqrt{2} \)
- Substitute and simplify: \( \frac{2}{2 \sqrt{2}} = \frac{1}{\sqrt{2}} \)
- Rationalize the denominator: \( \frac{1 \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}} = \frac{\sqrt{2}}{2} \)
- Problem 3: Solve for \( x \) in terms of \( \frac{1}{\sqrt{2}} \):
If \( \sin(x) = \frac{1}{\sqrt{2}} \), what is \( x \)?
Solution: \( x = 45^\circ \) or \( x = \frac{\pi}{4} \) radians.
READ MORE:
Rationalize the Denominator 1/ Căn Bậc Hai của 2