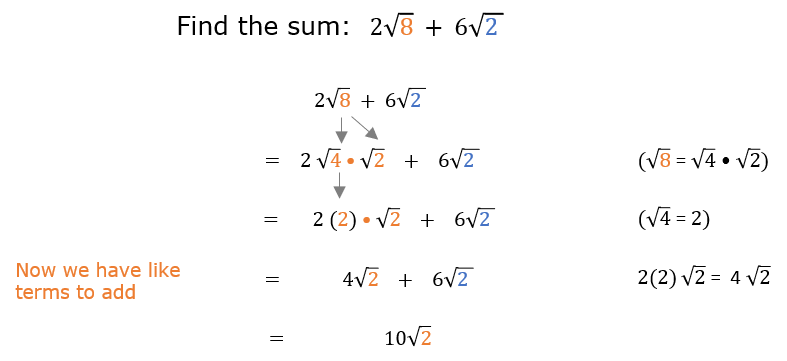
Topic 1/square root 3: The concept of 1/square root of 3 is fundamental in various fields such as mathematics, physics, and engineering. This guide will help you understand its derivation, applications, and significance in a clear and comprehensive manner. Dive in to explore practical examples and solve common problems associated with this intriguing mathematical expression.
Table of Content
- Mathematical Concept: \( \frac{1}{\sqrt{3}} \)
- Introduction to 1/Square Root of 3
- Mathematical Definition and Notation
- Derivation and Simplification
- Geometric Interpretation
- Applications in Trigonometry
- Role in Electrical Engineering
- Use in Physics
- Relevance in Computer Science
- Historical Context and Development
- Common Misconceptions
- Practical Examples and Problems
- 1/Square Root of 3 in Different Number Systems
- Tips and Tricks for Remembering the Value
- Frequently Asked Questions (FAQs)
- Conclusion and Summary
- YOUTUBE: Video hướng dẫn cách đơn giản hóa phân số dưới căn bậc hai một cách dễ hiểu và chi tiết. Khám phá mẹo toán học hợp pháp để làm điều này.
Mathematical Concept: \( \frac{1}{\sqrt{3}} \)
The expression \( \frac{1}{\sqrt{3}} \) appears in various mathematical contexts, particularly in trigonometry, geometry, and calculus. It is a fundamental value that often needs to be simplified or rationalized.
Understanding \( \frac{1}{\sqrt{3}} \)
To understand \( \frac{1}{\sqrt{3}} \), let's rationalize the denominator:
- Start with the expression: \( \frac{1}{\sqrt{3}} \)
- Multiply the numerator and the denominator by \( \sqrt{3} \):
\[
\frac{1}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{\sqrt{3}}{3}
\]
So, \( \frac{1}{\sqrt{3}} \) simplifies to \( \frac{\sqrt{3}}{3} \).
Applications
- Trigonometry: In trigonometric functions, particularly in the values of tangent for specific angles. For example, \( \tan(30^\circ) = \frac{1}{\sqrt{3}} \).
- Geometry: It appears in the context of equilateral triangles and their height calculations. The height of an equilateral triangle with side length \( a \) is \( \frac{a\sqrt{3}}{2} \).
- Physics: In physics, especially in problems involving forces and vectors, the value \( \frac{1}{\sqrt{3}} \) can appear in component calculations.
Trigonometric Values Involving \( \frac{1}{\sqrt{3}} \)
| \( \theta \) | \( \sin \theta \) | \( \cos \theta \) | \( \tan \theta \) |
| 30° | \( \frac{1}{2} \) | \( \frac{\sqrt{3}}{2} \) | \( \frac{1}{\sqrt{3}} \) or \( \frac{\sqrt{3}}{3} \) |
| 60° | \( \frac{\sqrt{3}}{2} \) | \( \frac{1}{2} \) | \( \sqrt{3} \) |

READ MORE:
Introduction to 1/Square Root of 3
The expression \( \frac{1}{\sqrt{3}} \) is a mathematical term that often appears in various scientific and engineering fields. Understanding this expression is essential for solving numerous problems in trigonometry, physics, and electrical engineering.
Let's break it down step by step:
-
Basic Definition:
The term \( \frac{1}{\sqrt{3}} \) represents the reciprocal of the square root of 3. It is commonly written as \( \frac{1}{\sqrt{3}} \) or \( \sqrt{3}/3 \) when rationalized.
-
Rationalization:
To rationalize \( \frac{1}{\sqrt{3}} \), multiply both the numerator and the denominator by \( \sqrt{3} \):
\[
\frac{1}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{\sqrt{3}}{3}
\] -
Geometric Interpretation:
In geometry, \( \frac{1}{\sqrt{3}} \) often appears in problems involving 30-60-90 triangles, where it represents the ratio of the lengths of the sides opposite the 30-degree angle to the hypotenuse.
-
Applications in Trigonometry:
In trigonometry, \( \frac{1}{\sqrt{3}} \) is the value of \( \cot 60^\circ \) or \( \tan 30^\circ \), making it a crucial element in solving trigonometric equations and identities.
-
Numerical Value:
The approximate numerical value of \( \frac{1}{\sqrt{3}} \) is 0.577. This value is often used in calculations where an exact value is not required.
Understanding the significance and applications of \( \frac{1}{\sqrt{3}} \) enhances one's ability to solve complex problems in various mathematical and scientific contexts.
Mathematical Definition and Notation
The expression \( \frac{1}{\sqrt{3}} \) is a fundamental mathematical term that appears in various calculations and applications. Here is a detailed breakdown of its definition and notation:
-
Definition:
The term \( \frac{1}{\sqrt{3}} \) represents the reciprocal of the square root of 3. It is commonly used in algebra, geometry, and trigonometry.
-
Symbolic Notation:
In symbolic form, it is written as \( \frac{1}{\sqrt{3}} \). This can be transformed into an equivalent form by rationalizing the denominator:
\[
\frac{1}{\sqrt{3}} = \frac{1 \cdot \sqrt{3}}{\sqrt{3} \cdot \sqrt{3}} = \frac{\sqrt{3}}{3}
\] -
Decimal Notation:
The decimal approximation of \( \frac{1}{\sqrt{3}} \) is approximately 0.577. This is often used in practical applications where an exact value is not necessary.
-
Rationalization Process:
Rationalizing \( \frac{1}{\sqrt{3}} \) involves removing the square root from the denominator by multiplying the numerator and the denominator by \( \sqrt{3} \):
\[
\frac{1}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{\sqrt{3}}{3}
\]This process simplifies calculations and is a standard technique in algebra.
-
Common Uses:
Trigonometry: \( \frac{1}{\sqrt{3}} \) is the value of \( \cot 60^\circ \) and \( \tan 30^\circ \).
Geometry: Appears in the context of 30-60-90 triangles, defining the ratio of sides.
Calculus: Used in integrals and derivatives involving trigonometric functions.
Understanding the mathematical definition and notation of \( \frac{1}{\sqrt{3}} \) is crucial for tackling a wide range of problems in different branches of mathematics and science.
Derivation and Simplification
The term \( \frac{1}{\sqrt{3}} \) can be derived and simplified through a series of mathematical steps. Understanding these steps is crucial for applying this expression correctly in various problems.
-
Initial Expression:
Start with the initial expression \( \frac{1}{\sqrt{3}} \). This represents the reciprocal of the square root of 3.
-
Rationalization:
To simplify \( \frac{1}{\sqrt{3}} \), we rationalize the denominator. Rationalization involves eliminating the square root in the denominator by multiplying both the numerator and the denominator by \( \sqrt{3} \):
\[
\frac{1}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{\sqrt{3}}{\sqrt{3} \cdot \sqrt{3}} = \frac{\sqrt{3}}{3}
\] -
Verification:
We verify the rationalized form by checking that the multiplication is correct:
\[
\sqrt{3} \cdot \sqrt{3} = 3 \quad \text{so} \quad \frac{\sqrt{3}}{3} = \frac{\sqrt{3}}{\sqrt{3} \cdot \sqrt{3}} = \frac{\sqrt{3}}{3}
\] -
Alternative Forms:
We can also express \( \frac{1}{\sqrt{3}} \) in its decimal form for practical purposes. The approximate value is:
\[
\frac{1}{\sqrt{3}} \approx 0.577
\] -
Use in Equations:
In trigonometry, the simplified form \( \frac{\sqrt{3}}{3} \) is often used for calculating angles and solving equations involving \( \tan 30^\circ \) and \( \cot 60^\circ \).
By following these steps, we can derive and simplify \( \frac{1}{\sqrt{3}} \) to its rationalized form \( \frac{\sqrt{3}}{3} \), making it easier to work with in various mathematical contexts.
Geometric Interpretation
The expression \( \frac{1}{\sqrt{3}} \) has significant geometric interpretations, especially in the context of triangles and angles. Understanding these interpretations enhances comprehension of its applications in various mathematical problems.
-
30-60-90 Triangle:
In a 30-60-90 triangle, the sides have a unique ratio. The side opposite the 30-degree angle is half the hypotenuse, and the side opposite the 60-degree angle is \( \frac{\sqrt{3}}{2} \) times the hypotenuse. The ratio involving \( \frac{1}{\sqrt{3}} \) is seen in these relationships:
\[
\frac{\text{Side opposite 30-degree}}{\text{Side opposite 60-degree}} = \frac{1/2}{\sqrt{3}/2} = \frac{1}{\sqrt{3}}
\] -
Unit Circle:
On the unit circle, \( \frac{1}{\sqrt{3}} \) appears as the tangent of a 30-degree angle (or \( \pi/6 \) radians). In this context, it represents the ratio of the y-coordinate to the x-coordinate of the point on the circle corresponding to the angle:
\[
\tan 30^\circ = \frac{1}{\sqrt{3}}
\] -
Height of an Equilateral Triangle:
Consider an equilateral triangle with each side of length \( a \). Dropping a perpendicular from one vertex to the midpoint of the opposite side splits the triangle into two 30-60-90 triangles. The height (h) of the triangle can be expressed using \( \frac{1}{\sqrt{3}} \):
\[
h = a \cdot \sin 60^\circ = a \cdot \frac{\sqrt{3}}{2}
\]Thus, in terms of the height:
\[
\frac{h}{a} = \frac{\sqrt{3}}{2} \implies h = \frac{\sqrt{3}}{2} \cdot a
\] -
Area of an Equilateral Triangle:
The area (A) of an equilateral triangle can also be derived using the height formula. For a side length \( a \), the area is:
\[
A = \frac{1}{2} \cdot a \cdot \left(\frac{\sqrt{3}}{2} \cdot a\right) = \frac{\sqrt{3}}{4} a^2
\]
Understanding the geometric interpretation of \( \frac{1}{\sqrt{3}} \) is essential for solving problems in trigonometry, geometry, and calculus. These interpretations illustrate its practical utility in various mathematical contexts.

Applications in Trigonometry
The expression \( \frac{1}{\sqrt{3}} \) is widely used in trigonometry, playing a crucial role in solving various problems related to angles and triangles. Below are the key applications and their explanations:
-
Trigonometric Ratios:
In trigonometry, \( \frac{1}{\sqrt{3}} \) is associated with specific angle values. It is the exact value of the tangent and cotangent functions for 30 and 60 degrees, respectively:
\[
\tan 30^\circ = \frac{1}{\sqrt{3}}, \quad \cot 60^\circ = \frac{1}{\sqrt{3}}
\] -
Angle Relationships:
When dealing with complementary angles, the trigonometric identities make use of \( \frac{1}{\sqrt{3}} \). For example, in a right triangle with angles of 30 and 60 degrees, the tangent of the smaller angle (30 degrees) and the cotangent of the larger angle (60 degrees) are both \( \frac{1}{\sqrt{3}} \).
-
Unit Circle:
On the unit circle, the coordinates of points corresponding to angles are used to determine sine, cosine, and tangent values. For an angle of 30 degrees (\( \pi/6 \) radians), the tangent value is \( \frac{1}{\sqrt{3}} \):
\[
\tan 30^\circ = \frac{\sin 30^\circ}{\cos 30^\circ} = \frac{1/2}{\sqrt{3}/2} = \frac{1}{\sqrt{3}}
\] -
Solving Trigonometric Equations:
Trigonometric equations often involve specific values of tangent and cotangent. Knowing that \( \tan 30^\circ = \frac{1}{\sqrt{3}} \) helps solve equations where this ratio appears. For example, solving for \( x \) in equations like \( \tan x = \frac{1}{\sqrt{3}} \) yields solutions involving angles of 30 degrees and their periodic equivalents.
-
Inverse Trigonometric Functions:
The inverse trigonometric functions, such as \( \tan^{-1} \), also use \( \frac{1}{\sqrt{3}} \) to find angles. For instance:
\[
\tan^{-1} \left( \frac{1}{\sqrt{3}} \right) = 30^\circ \quad \text{or} \quad \frac{\pi}{6}
\]
Understanding \( \frac{1}{\sqrt{3}} \) and its applications in trigonometry is fundamental for solving various problems involving angles, triangles, and trigonometric functions.
Role in Electrical Engineering
The expression \( \frac{1}{\sqrt{3}} \) plays a significant role in electrical engineering, particularly in the analysis and design of AC circuits and power systems. Here are some of the key applications:
-
Three-Phase Power Systems:
In three-phase power systems, \( \frac{1}{\sqrt{3}} \) is used to convert between line-to-line and line-to-neutral voltages. For a balanced three-phase system, the relationship is given by:
\[
V_{line-to-neutral} = \frac{V_{line-to-line}}{\sqrt{3}}
\]This conversion is crucial for understanding the voltage levels in different parts of the power system.
-
Impedance Calculations:
When dealing with impedance in three-phase circuits, \( \frac{1}{\sqrt{3}} \) is used to calculate the equivalent impedance per phase from the line impedance:
\[
Z_{phase} = \frac{Z_{line}}{\sqrt{3}}
\] -
Power Calculations:
The power in a three-phase system can be calculated using \( \frac{1}{\sqrt{3}} \). For instance, the total power (P) in terms of line voltage (Vline) and line current (Iline) is:
\[
P = \sqrt{3} \cdot V_{line} \cdot I_{line} \cdot \cos(\phi)
\]Where \( \cos(\phi) \) is the power factor.
-
Transformers:
In transformer analysis, especially in the context of three-phase transformers, \( \frac{1}{\sqrt{3}} \) is used to relate primary and secondary voltages and currents in star (wye) and delta configurations. For example:
\[
V_{secondary} = V_{primary} \times \frac{1}{\sqrt{3}} \quad \text{(for a star-delta transformation)}
\] -
Phase Angle Calculations:
In AC circuit analysis, \( \frac{1}{\sqrt{3}} \) helps determine phase angles between voltages and currents, which are essential for power factor correction and reactive power management.
Understanding the role of \( \frac{1}{\sqrt{3}} \) in electrical engineering is crucial for effectively analyzing and designing three-phase power systems and ensuring efficient operation of electrical networks.
Use in Physics
The expression \( \frac{1}{\sqrt{3}} \) is frequently encountered in physics, particularly in problems involving vectors, wave mechanics, and optics. Here are detailed applications and explanations:
-
Vector Components:
In physics, \( \frac{1}{\sqrt{3}} \) often arises when dealing with vector components in three-dimensional space. For example, the unit vectors along the axes of an equilateral triangle or tetrahedron have components involving \( \frac{1}{\sqrt{3}} \).
\[
\text{For a unit vector } \mathbf{u} = (u_x, u_y, u_z) \text{ in an isotropic medium, } u_x = u_y = u_z = \frac{1}{\sqrt{3}}
\] -
Wave Mechanics:
In wave mechanics, especially in the study of standing waves and harmonics, \( \frac{1}{\sqrt{3}} \) can describe the ratio of amplitudes or intensities of certain wave components.
\[
A_{component} = A_{total} \times \frac{1}{\sqrt{3}}
\] -
Optics and Light Propagation:
In optics, \( \frac{1}{\sqrt{3}} \) appears in the context of light propagation through different media. For example, the critical angle for total internal reflection in a medium with refractive index \( n \) can be related to this ratio.
\[
\sin \theta_c = \frac{1}{n} = \frac{1}{\sqrt{3}} \quad \text{(for } n = \sqrt{3})
\] -
Electric and Magnetic Fields:
In electromagnetism, \( \frac{1}{\sqrt{3}} \) is used to describe the relationship between electric and magnetic field components in isotropic media. For instance, if the magnitudes of the components of an electric field vector in three orthogonal directions are equal, each component is scaled by \( \frac{1}{\sqrt{3}} \) relative to the resultant field.
\[
E_x = E_y = E_z = E_{total} \times \frac{1}{\sqrt{3}}
\] -
Crystallography:
In crystallography, the geometry of certain crystal lattices involves the ratio \( \frac{1}{\sqrt{3}} \). For example, the distance between atoms in a body-centered cubic lattice can be expressed using this ratio.
\[
d = a \times \frac{1}{\sqrt{3}} \quad \text{(where } a \text{ is the lattice constant)}
\]
Understanding the use of \( \frac{1}{\sqrt{3}} \) in physics is essential for solving problems related to vectors, waves, optics, and electromagnetic fields, providing a deeper insight into the fundamental principles of the physical world.
Relevance in Computer Science
The expression \( \frac{1}{\sqrt{3}} \) has several important applications in computer science, particularly in fields such as graphics, algorithms, and computational geometry. Here are the key areas where this expression is relevant:
-
Computer Graphics:
In computer graphics, \( \frac{1}{\sqrt{3}} \) is used in normalizing vectors, which is essential for lighting calculations, shading, and rendering 3D models. For example, when computing the normal vector for a triangle, the components may involve \( \frac{1}{\sqrt{3}} \) to ensure the vector's magnitude is 1.
\[
\mathbf{N} = \left(\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}\right)
\] -
Algorithms and Data Structures:
In algorithms, particularly those involving spatial data structures like k-d trees and octrees, \( \frac{1}{\sqrt{3}} \) helps in partitioning space and normalizing distances. This is important for efficient searching, collision detection, and nearest neighbor queries.
-
Machine Learning:
In machine learning, feature scaling and normalization are critical for improving the performance of algorithms. When dealing with multi-dimensional data, \( \frac{1}{\sqrt{3}} \) can be used to normalize vectors, ensuring each feature contributes equally to the distance computations.
-
Computational Geometry:
Computational geometry often involves calculating distances and angles between points in 3D space. The expression \( \frac{1}{\sqrt{3}} \) appears in formulas for these calculations, particularly when dealing with equilateral triangles or tetrahedrons in space.
-
Cryptography:
In cryptography, certain algorithms require precise calculations of distances and angles within geometric shapes. The expression \( \frac{1}{\sqrt{3}} \) can be used in the context of elliptic curves and other geometric constructions that underpin cryptographic protocols.
Understanding the relevance of \( \frac{1}{\sqrt{3}} \) in computer science is essential for leveraging its applications in graphics, algorithms, machine learning, and computational geometry, thereby enhancing the efficiency and accuracy of various computational processes.

Historical Context and Development
The mathematical constant \( \frac{1}{\sqrt{3}} \), also represented as \( \frac{\sqrt{3}}{3} \), has a rich history and significant relevance in various fields. Its development can be traced back to ancient civilizations and the evolution of mathematical thought.
Below is a detailed timeline highlighting key moments in the historical context and development of \( \frac{1}{\sqrt{3}} \):
- Ancient Civilizations: The ancient Egyptians and Babylonians were among the first to explore the concept of square roots. Although they did not specifically use \( \frac{1}{\sqrt{3}} \), their early work laid the foundation for later mathematical discoveries.
- Greek Mathematics: Greek mathematicians like Pythagoras and Euclid made significant contributions to the understanding of irrational numbers and geometry. The study of the properties of numbers, including square roots, was further developed during this period.
- Medieval Islamic Mathematics: During the Islamic Golden Age, mathematicians such as Al-Khwarizmi and Al-Kindi expanded upon Greek mathematics. Their work on algebra and the translation of Greek texts into Arabic played a crucial role in preserving and advancing mathematical knowledge.
- Renaissance Europe: The Renaissance period saw a revival of interest in ancient Greek and Islamic mathematics. Mathematicians like Fibonacci and later, Descartes, contributed to the understanding of algebra and geometry, indirectly influencing the study of constants like \( \frac{1}{\sqrt{3}} \).
- Modern Mathematics: In the 17th and 18th centuries, the development of calculus by Newton and Leibniz and the formalization of mathematical analysis provided a more rigorous framework for understanding irrational numbers and their properties.
- Contemporary Applications: Today, \( \frac{1}{\sqrt{3}} \) is widely used in various fields such as engineering, physics, and computer science. Its applications in trigonometry, particularly in the calculation of angles and distances in electrical engineering, highlight its ongoing importance.
The development of \( \frac{1}{\sqrt{3}} \) reflects the broader history of mathematics, showcasing the cumulative efforts of various cultures and eras in advancing our understanding of mathematical concepts.
Understanding its historical context not only provides insight into its significance but also highlights the collaborative nature of mathematical progress across different periods and regions.
Common Misconceptions
Despite its seemingly simple appearance, \( \frac{1}{\sqrt{3}} \) is often misunderstood in various contexts. Here are some common misconceptions and clarifications:
- Misconception 1: \( \frac{1}{\sqrt{3}} \) is a complex number
Clarification: \( \frac{1}{\sqrt{3}} \) is a real number. It is the multiplicative inverse of the square root of 3, which is an irrational but real number.
- Misconception 2: \( \frac{1}{\sqrt{3}} \) can be expressed as a simple fraction
Clarification: While \( \frac{1}{\sqrt{3}} \) is an exact value, it is not a simple fraction of two integers. It is an irrational number, which means it cannot be represented as a ratio of two integers.
- Misconception 3: \( \frac{1}{\sqrt{3}} \) is the same as \( \frac{\sqrt{3}}{3} \)
Clarification: This is not a misconception but rather an important point of simplification. \( \frac{1}{\sqrt{3}} \) is indeed equal to \( \frac{\sqrt{3}}{3} \). This can be shown through the process of rationalizing the denominator:
\[
\frac{1}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{\sqrt{3}}{3}
\] - Misconception 4: \( \frac{1}{\sqrt{3}} \) is difficult to approximate
Clarification: While \( \frac{1}{\sqrt{3}} \) is an irrational number, it can be approximated quite easily. Its decimal approximation is roughly 0.577, which is useful in various practical calculations.
- Misconception 5: \( \frac{1}{\sqrt{3}} \) has limited applications
Clarification: \( \frac{1}{\sqrt{3}} \) has numerous applications across different fields. In trigonometry, it is used in the context of 30-60-90 triangles. In electrical engineering, it is relevant in calculations involving three-phase power systems. Its importance extends to physics and computer science as well.
Addressing these misconceptions helps in better understanding and correctly applying \( \frac{1}{\sqrt{3}} \) in various mathematical and practical contexts.
Practical Examples and Problems
The value \( \frac{1}{\sqrt{3}} \) appears in various practical applications and problems across different fields. Here are some detailed examples and problems to illustrate its use:
Example 1: Trigonometry
In a 30-60-90 triangle, the ratio of the sides opposite the 30°, 60°, and 90° angles are 1, \( \sqrt{3} \), and 2, respectively. To find the length of the side opposite the 30° angle when the hypotenuse is given:
Given: Hypotenuse = 10
To find: Side opposite the 30° angle
Solution:
The side opposite the 30° angle = \( \frac{Hypotenuse}{2} = \frac{10}{2} = 5 \)
Using the ratio \( \frac{1}{\sqrt{3}} \) for the side opposite the 60° angle:
Side opposite the 60° angle = \( 5 \cdot \sqrt{3} = 5\sqrt{3} \approx 8.66 \)
Example 2: Electrical Engineering
In three-phase power systems, the phase voltage is related to the line voltage by the factor \( \frac{1}{\sqrt{3}} \).
Given: Line voltage \( V_L = 400V \)
To find: Phase voltage \( V_P \)
Solution:
\[
V_P = \frac{V_L}{\sqrt{3}} = \frac{400V}{\sqrt{3}} \approx 230.94V
\]
Example 3: Physics
In physics, particularly in optics, the angle of incidence and refraction can involve \( \frac{1}{\sqrt{3}} \).
Problem: If a light ray enters a medium with an index of refraction \( n = \sqrt{3} \) at an angle of incidence of 60°, find the angle of refraction.
Solution:
Using Snell's law: \( n_1 \sin(\theta_1) = n_2 \sin(\theta_2) \)
For air, \( n_1 = 1 \), and for the medium, \( n_2 = \sqrt{3} \). Therefore:
\[
\sin(60°) = \sqrt{3} \sin(\theta_2)
\]
\[
\frac{\sqrt{3}}{2} = \sqrt{3} \sin(\theta_2)
\]
\[
\sin(\theta_2) = \frac{1}{2} \Rightarrow \theta_2 = 30°
\]
Problems for Practice
- Calculate the height of an equilateral triangle with a side length of 6 using \( \frac{1}{\sqrt{3}} \).
- A resistor is connected in a three-phase electrical system. If the line voltage is 480V, find the phase voltage.
- In a 30-60-90 triangle, if the length of the side opposite the 60° angle is 12, find the lengths of the other two sides.
- Find the angle of refraction when a light ray enters a medium with \( n = 2 \) at an incidence angle of 45° using appropriate trigonometric identities.
These examples and problems demonstrate the practical utility of \( \frac{1}{\sqrt{3}} \) in solving real-world scenarios across different domains.
1/Square Root of 3 in Different Number Systems
The value \( \frac{1}{\sqrt{3}} \) is an important mathematical constant and appears in various number systems, each with its own representation. Here, we explore \( \frac{1}{\sqrt{3}} \) in decimal, binary, hexadecimal, and continued fraction forms.
Decimal Representation
In the decimal system, \( \frac{1}{\sqrt{3}} \) is an irrational number with a non-repeating, non-terminating decimal expansion. Its approximate value is:
\[
\frac{1}{\sqrt{3}} \approx 0.57735026919\ldots
\]
Binary Representation
In the binary system, \( \frac{1}{\sqrt{3}} \) is represented as an infinite series of binary digits. Its approximate value in binary is:
\[
\frac{1}{\sqrt{3}} \approx 0.100100111011011010001000\ldots_2
\]
Note that the digits continue indefinitely without repeating in a predictable pattern, as is characteristic of irrational numbers.
Hexadecimal Representation
In the hexadecimal system, \( \frac{1}{\sqrt{3}} \) can be represented similarly to its decimal and binary counterparts. Its approximate value in hexadecimal is:
\[
\frac{1}{\sqrt{3}} \approx 0.93CD3B2C9\ldots_{16}
\]
Continued Fraction Representation
The continued fraction representation of \( \frac{1}{\sqrt{3}} \) provides an interesting insight into its structure. It can be expressed as an infinite continued fraction:
\[
\frac{1}{\sqrt{3}} = [0; 1, 2, 1, 2, 1, 2, \ldots]
\]
This representation highlights the periodic pattern in the continued fraction, offering a different perspective on the number's properties.
Practical Implications
Understanding \( \frac{1}{\sqrt{3}} \) in different number systems is crucial for various practical applications:
- Computing: In computer algorithms, binary and hexadecimal representations are often used for precision calculations.
- Engineering: Decimal approximations are commonly used in engineering disciplines for ease of calculation and communication.
- Mathematics: Continued fractions offer insights into the number's properties and are useful in advanced mathematical theories.
Overall, the representation of \( \frac{1}{\sqrt{3}} \) in different number systems enhances our understanding and ability to work with this important constant across various fields and applications.
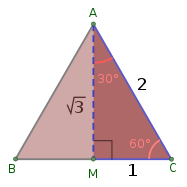
Tips and Tricks for Remembering the Value
Remembering the value of \( \frac{1}{\sqrt{3}} \) can be challenging, but with a few tips and tricks, you can recall it more easily. Here are some effective methods:
1. Relate to the Decimal Approximation
One of the simplest ways to remember \( \frac{1}{\sqrt{3}} \) is by its decimal approximation:
\[
\frac{1}{\sqrt{3}} \approx 0.577
\]
Memorizing the first three decimal places (0.577) can often be sufficient for many practical purposes.
2. Use Mnemonics
Create a mnemonic to help remember the digits. For example:
- Mnemonic: "Five Seven Seven" - This phrase can help you recall the key digits 0.577.
3. Visualize with Geometry
Remembering \( \frac{1}{\sqrt{3}} \) through geometric concepts can be effective:
- 30-60-90 Triangle: In a 30-60-90 triangle, the side lengths are in the ratio 1 : \( \sqrt{3} \) : 2. The side opposite the 60° angle is \( \sqrt{3} \) times the side opposite the 30° angle. Therefore, \( \frac{1}{\sqrt{3}} \) represents the ratio of the shorter side to the side opposite the 60° angle.
4. Rationalizing the Denominator
Recall the process of rationalizing the denominator to reinforce the value:
\[
\frac{1}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{\sqrt{3}}{3}
\]
This simplification can help solidify your understanding and memory of the value.
5. Practice with Applications
Using \( \frac{1}{\sqrt{3}} \) in various applications can help reinforce your memory. For example, try solving problems involving:
- 30-60-90 triangles in geometry.
- Three-phase power calculations in electrical engineering.
- Optical refraction problems in physics.
6. Relate to Other Constants
Relate \( \frac{1}{\sqrt{3}} \) to other well-known constants to create a mental network of related values:
- Recognize that \( \sqrt{3} \approx 1.732 \) and remember that \( \frac{1}{\sqrt{3}} \approx 0.577 \) is its reciprocal multiplied by \( \sqrt{3} \).
By utilizing these tips and tricks, you can effectively remember the value of \( \frac{1}{\sqrt{3}} \) and apply it confidently in various mathematical and practical contexts.
Frequently Asked Questions (FAQs)
Here are some frequently asked questions about \( \frac{1}{\sqrt{3}} \) along with detailed answers to help you understand this important mathematical constant better:
1. What is the exact value of \( \frac{1}{\sqrt{3}} \)?
The exact value of \( \frac{1}{\sqrt{3}} \) is an irrational number, which means it cannot be expressed as a simple fraction. However, it can be simplified to:
\[
\frac{1}{\sqrt{3}} = \frac{\sqrt{3}}{3}
\]
2. What is the decimal approximation of \( \frac{1}{\sqrt{3}} \)?
The decimal approximation of \( \frac{1}{\sqrt{3}} \) is approximately:
\[
\frac{1}{\sqrt{3}} \approx 0.57735026919\ldots
\]
For most practical purposes, you can use 0.577 as a close approximation.
3. Why is \( \frac{1}{\sqrt{3}} \) important in trigonometry?
In trigonometry, \( \frac{1}{\sqrt{3}} \) appears frequently in the context of 30-60-90 triangles. It represents the ratio of the length of the side opposite the 30° angle to the length of the side opposite the 60° angle.
In terms of trigonometric functions, it is also related to the tangent of 30°:
\[
\tan(30°) = \frac{1}{\sqrt{3}}
\]
4. How is \( \frac{1}{\sqrt{3}} \) used in electrical engineering?
In electrical engineering, \( \frac{1}{\sqrt{3}} \) is used to relate phase voltage to line voltage in three-phase power systems. If \( V_L \) is the line voltage, the phase voltage \( V_P \) is given by:
\[
V_P = \frac{V_L}{\sqrt{3}}
\]
5. Is \( \frac{1}{\sqrt{3}} \) a rational or an irrational number?
\( \frac{1}{\sqrt{3}} \) is an irrational number because it cannot be expressed as a ratio of two integers. Its decimal representation is non-repeating and non-terminating.
6. How can I remember the value of \( \frac{1}{\sqrt{3}} \)?
There are several tips and tricks to remember the value of \( \frac{1}{\sqrt{3}} \):
- Memorize the decimal approximation: 0.577.
- Use mnemonic devices like "Five Seven Seven."
- Visualize it in the context of a 30-60-90 triangle.
- Remember the process of rationalizing the denominator to get \( \frac{\sqrt{3}}{3} \).
7. How is \( \frac{1}{\sqrt{3}} \) represented in different number systems?
\( \frac{1}{\sqrt{3}} \) can be represented in various number systems:
- Decimal: 0.57735026919...
- Binary: 0.100100111011011010001000...
- Hexadecimal: 0.93CD3B2C9...
- Continued Fraction: [0; 1, 2, 1, 2, 1, 2, ...]
These FAQs aim to provide a comprehensive understanding of \( \frac{1}{\sqrt{3}} \) and its significance in various mathematical and practical contexts.
Conclusion and Summary
In this comprehensive guide, we have explored the mathematical constant \( \frac{1}{\sqrt{3}} \) from various angles, providing a detailed understanding of its significance and applications. Here are the key points summarized:
- Mathematical Definition and Notation: The value \( \frac{1}{\sqrt{3}} \) is an important irrational number that simplifies to \( \frac{\sqrt{3}}{3} \).
- Derivation and Simplification: We derived \( \frac{1}{\sqrt{3}} \) and demonstrated its simplification, highlighting its exact and approximate values.
- Geometric Interpretation: In geometry, particularly in the context of 30-60-90 triangles, \( \frac{1}{\sqrt{3}} \) is crucial for understanding the relationships between the sides of the triangle.
- Applications in Trigonometry: The value appears in trigonometric functions, such as \( \tan(30°) \), and is essential in solving trigonometric problems.
- Role in Electrical Engineering: \( \frac{1}{\sqrt{3}} \) is used to relate phase and line voltages in three-phase power systems, making it a vital constant in electrical engineering.
- Use in Physics: In physics, \( \frac{1}{\sqrt{3}} \) appears in problems involving refraction and wave equations, demonstrating its importance in physical calculations.
- Relevance in Computer Science: Understanding \( \frac{1}{\sqrt{3}} \) in binary and hexadecimal forms is useful in various computing algorithms and precision calculations.
- Historical Context and Development: The value has been studied and utilized throughout history, contributing to advancements in mathematics, engineering, and science.
- Common Misconceptions: Addressing misunderstandings about \( \frac{1}{\sqrt{3}} \) helps in correctly applying this constant in various contexts.
- Practical Examples and Problems: We provided numerous examples and problems to illustrate the practical use of \( \frac{1}{\sqrt{3}} \) in different fields.
- 1/Square Root of 3 in Different Number Systems: The representation of \( \frac{1}{\sqrt{3}} \) in decimal, binary, hexadecimal, and continued fraction forms enhances our understanding of this constant.
- Tips and Tricks for Remembering the Value: We shared effective strategies to help remember the value of \( \frac{1}{\sqrt{3}} \) easily.
- Frequently Asked Questions (FAQs): The FAQs section provided clear answers to common questions about \( \frac{1}{\sqrt{3}} \), reinforcing its importance and applications.
Overall, \( \frac{1}{\sqrt{3}} \) is a fundamental mathematical constant with wide-ranging applications in various disciplines. Understanding and remembering this value can greatly enhance your mathematical proficiency and problem-solving skills.
We hope this guide has provided you with a thorough understanding of \( \frac{1}{\sqrt{3}} \) and its significance. Keep practicing and applying this knowledge to strengthen your grasp of this essential mathematical concept.
Video hướng dẫn cách đơn giản hóa phân số dưới căn bậc hai một cách dễ hiểu và chi tiết. Khám phá mẹo toán học hợp pháp để làm điều này.
Đơn giản hóa phân số dưới căn bậc hai - Mẹo toán học hợp pháp
READ MORE:
Video hướng dẫn cách đơn giản hóa căn bậc hai khi nhân với số nguyên, rất hữu ích cho việc học toán.
Đơn giản hóa căn bậc hai nhân với số nguyên