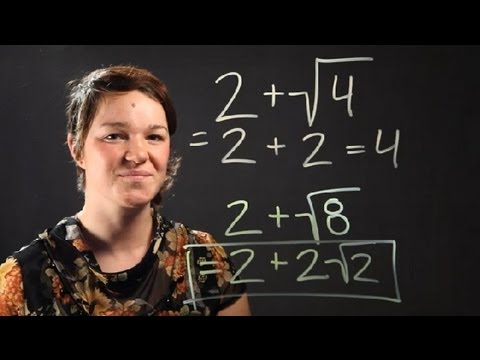Topic adding square roots with variables: Adding square roots with variables can seem daunting, but with a few simple steps, you can master this mathematical concept. Whether you are dealing with like terms or simplifying before adding, this guide will help you understand and apply the principles effectively.
Table of Content
- Adding Square Roots with Variables
- Introduction
- Basics of Square Roots
- Adding Square Roots
- Simplifying Square Roots Before Adding
- Adding Square Roots with Variables
- Advanced Techniques
- Common Mistakes to Avoid
- Practice Problems
- Conclusion
- YOUTUBE: Video này hướng dẫn cách rút gọn căn bậc hai có biến số, giúp bạn nắm vững kỹ năng cơ bản trong Toán học.
Adding Square Roots with Variables
Adding square roots with variables involves combining like terms, similar to the process used in algebra for combining like terms with variables.
Steps for Adding Square Roots
- Simplify each square root if possible.
- Combine like terms (square roots with the same radicand).
Examples
| Expression | Steps | Result |
|---|---|---|
| \(2\sqrt{2} - 7\sqrt{2}\) | Subtract coefficients | \(-5\sqrt{2}\) |
| \(8\sqrt{2} - 9\sqrt{2}\) | Subtract coefficients | \(-\sqrt{2}\) |
| \(5\sqrt{3} - 9\sqrt{3}\) | Subtract coefficients | \(-4\sqrt{3}\) |
| \(3\sqrt{y} + 4\sqrt{y}\) | Add coefficients | \(7\sqrt{y}\) |
| \(2\sqrt{x} + 7\sqrt{x}\) | Add coefficients | \(9\sqrt{x}\) |
Key Concepts
- Like Radicals: Square roots that have the same radicand (expression inside the radical).
- Simplify First: Always simplify the square roots before combining.
Additional Tips
- When the radicands are not the same, you cannot combine the square roots.
- Simplify complex expressions by breaking down the radicands into their prime factors.
Understanding and mastering the addition of square roots with variables will enhance your algebra skills and help in solving more complex mathematical problems.

READ MORE:
Introduction
Understanding how to add square roots with variables is a crucial skill in algebra. This process involves combining like terms where the radicands (the numbers under the square root) are the same. Here, we'll explore step-by-step methods to simplify and add square roots effectively, ensuring a solid grasp of these fundamental concepts.
-
Step 1: Simplify the Square Roots
Begin by simplifying each square root to its simplest form. For example, simplify \(\sqrt{18}\) to \(3\sqrt{2}\) and \(\sqrt{50}\) to \(5\sqrt{2}\). -
Step 2: Identify Like Terms
Combine the square roots that have the same radicands. For instance, \(3\sqrt{2} + 5\sqrt{2} = 8\sqrt{2}\). Only like terms can be combined in this manner. -
Step 3: Add or Subtract the Coefficients
Once the like terms are identified, add or subtract the coefficients (the numbers in front of the square roots). For example, \(2\sqrt{x} + 7\sqrt{x} = 9\sqrt{x}\). -
Examples
- Simplify \(2\sqrt{3} + 5\sqrt{3} - \sqrt{3}\): Combine like terms to get \(6\sqrt{3}\).
- Simplify \(3\sqrt{y} + 4\sqrt{y}\): Combine to get \(7\sqrt{y}\).
Basics of Square Roots
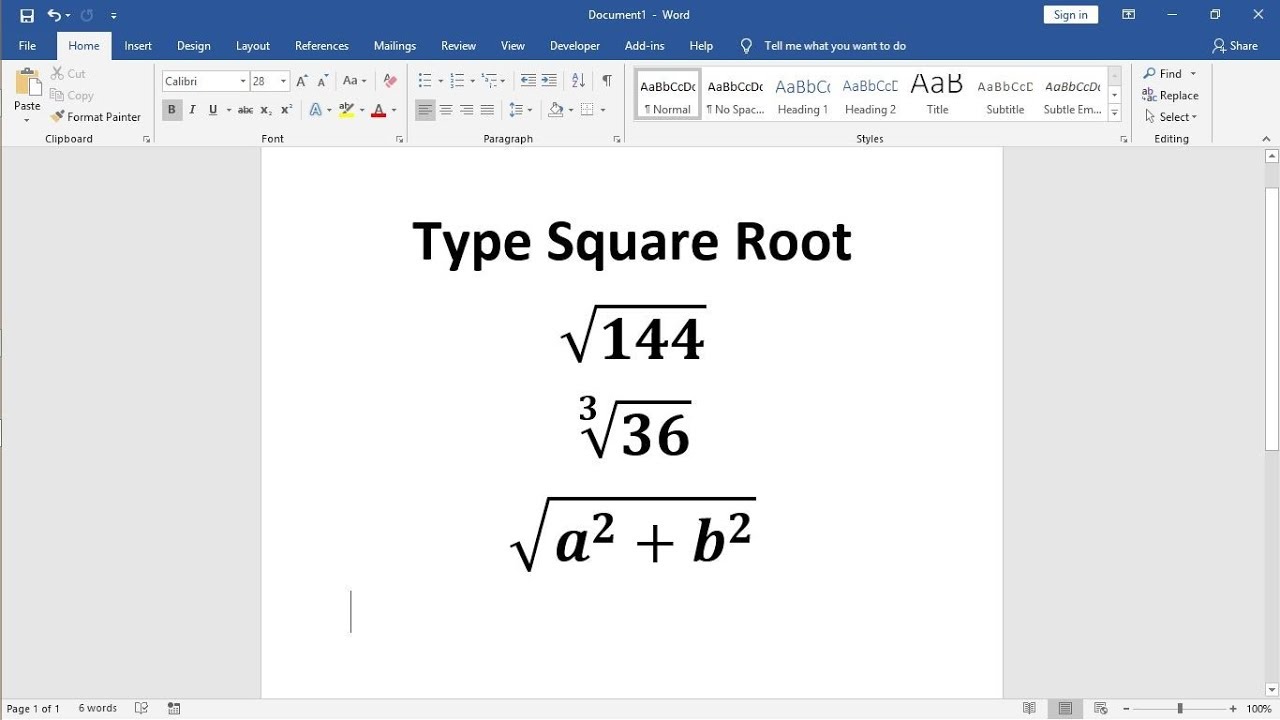
Square roots are fundamental components of algebra and are represented by the radical symbol (√). The square root of a number is a value that, when multiplied by itself, gives the original number. For example, √16 = 4 because 4 * 4 = 16.
When dealing with square roots that involve variables, the principles remain consistent. For instance, the square root of x2 is x, as x * x = x2. Let's explore the steps and rules for working with square roots, especially when variables are involved.
- Simplifying Square Roots: Simplify square roots by identifying and extracting perfect square factors. For example, √18 can be simplified to 3√2 because 18 = 9 * 2 and √9 = 3.
- Combining Like Terms: You can only add or subtract square roots with the same radicand (the number or expression inside the radical). For example, 3√5 + 2√5 = 5√5, but 3√5 + 2√3 cannot be combined.
- Simplifying Square Roots with Variables: When variables are involved, apply the same principles. For example, √(x4) = x2 because (x2)2 = x4.
Below are some key examples and steps to simplify and combine square roots:
| Expression | Step-by-Step Simplification | Result |
|---|---|---|
| √(16) | 16 is a perfect square. | 4 |
| √(x2) | Identify that x2 is a perfect square. | x |
| √(50) | 50 = 25 * 2, and √25 = 5. | 5√2 |
| 3√(x4) + 2√(x4) | Simplify each term: √(x4) = x2. | 3x2 + 2x2 = 5x2 |
| 2√(12) - √(3) | 12 = 4 * 3, and √4 = 2. | 2 * 2√3 - √3 = 4√3 - √3 = 3√3 |
By mastering these basics, you will be well-equipped to handle more complex problems involving square roots with variables. Remember to always look for perfect squares within the radicand and simplify before combining terms.
Adding Square Roots
Adding square roots involves combining radical expressions that have the same radicand. The process can be broken down into a few key steps to ensure accuracy and simplicity. Below is a detailed guide on how to add square roots.
- Simplify Each Square Root: Before adding, ensure each square root is in its simplest form. This might involve factoring out perfect squares from the radicand.
- Identify Like Terms: Only square roots with the same radicand (the number inside the square root) can be added together.
- Combine Coefficients: Once like terms are identified, combine their coefficients while keeping the radicand the same.
Let's illustrate these steps with a few examples:
| Example | Expression | Steps | Result |
| 1 | \(3\sqrt{2} + 5\sqrt{2}\) |
|
\(8\sqrt{2}\) |
| 2 | \(\sqrt{18} + \sqrt{8}\) |
|
\(5\sqrt{2}\) |
| 3 | \(2\sqrt{3} + 4\sqrt{5}\) |
|
Expression remains \(2\sqrt{3} + 4\sqrt{5}\) |
By following these steps, adding square roots can become a straightforward task. Always ensure to simplify each square root and identify like terms before combining the coefficients.
Simplifying Square Roots Before Adding
Before adding square roots with variables, it is crucial to simplify each square root. Simplifying helps in identifying like terms, which are necessary for addition. Here are the steps to simplify square roots:
- Identify the radicand (the number or expression inside the square root).
- Find the largest perfect square factor of the radicand.
- Rewrite the square root as a product of the square root of the perfect square and the square root of the remaining factor.
- Simplify the square root of the perfect square to get an integer.
- Multiply the integer by the remaining square root.
For example:
- Simplify :
- Factor 18 into 9 * 2.
- Rewrite as .
- Simplify to 3, so .
- Simplify :
- Factor 50 into 25 * 2.
- Rewrite as .
- Simplify to 5, so .
After simplifying the square roots, you can add them if they are like terms.
| Expression | Simplified |
Thus, always simplify square roots before adding them to ensure accurate results and combine like terms effectively.

Adding Square Roots with Variables
When adding square roots with variables, it's crucial to simplify each square root first and ensure they have the same radicand. Only then can they be combined. Below are detailed steps to add square roots with variables effectively.
- Simplify Each Square Root:
Begin by simplifying each square root expression. Simplify any numerical factors and variables under the square root separately. For example, simplify \(\sqrt{50x^2}\) as \(5x\sqrt{2}\).
- Identify Like Terms:
Identify terms with the same radicand. Terms like \(3\sqrt{2x}\) and \(5\sqrt{2x}\) can be combined because they share the same radicand \(\sqrt{2x}\).
- Combine Like Terms:
Add or subtract the coefficients of like terms. For instance, \(3\sqrt{2x} + 5\sqrt{2x} = 8\sqrt{2x}\).
By following these steps, you can accurately add square roots with variables, ensuring the expressions are fully simplified and correctly combined.
Advanced Techniques
When adding square roots with variables, several advanced techniques can be employed to simplify and combine the expressions effectively. These methods ensure accuracy and help in handling more complex algebraic problems.
- Simplifying Complex Radicals: Before adding, simplify each square root as much as possible. Factor out perfect squares and reduce the radicands to their simplest forms.
- Combining Like Terms: Identify and combine square roots with identical radicands. For example, .
- Using Algebraic Techniques: For square roots with different radicands, treat each term as an algebraic expression. If simplification is not possible, the expression remains as is, e.g., .
- Dealing with Variables: Simplify square roots containing variables by factoring the variables' exponents. For instance, .
- Rationalizing Expressions: When necessary, rationalize the denominator to simplify expressions further, especially in complex fractions involving square roots.
- Checking for Common Factors: Look for common factors in different radicands to simplify them into like terms. This can often reveal opportunities to combine and reduce the expression.
Mastering these advanced techniques for adding square roots with variables not only simplifies your calculations but also enhances your overall problem-solving skills in algebra.
Common Mistakes to Avoid
Adding square roots with variables can be tricky, and students often make mistakes that lead to incorrect results. Being aware of these common errors can help you improve your understanding and accuracy. Here are some of the most frequent mistakes to watch out for:
- Adding Unlike Terms: A common mistake is attempting to add square roots that are not like terms. You can only add square roots directly if their radicands (the numbers or expressions inside the square root) are identical. For example, you can add \( \sqrt{2} + 3\sqrt{2} \), but you cannot add \( \sqrt{2} + \sqrt{3} \).
- Incorrect Simplification: Failing to fully simplify square roots before adding them can lead to incorrect results. Ensure that each square root is simplified to its lowest form to identify like terms accurately. For instance, simplify \( \sqrt{18} \) to \( 3\sqrt{2} \) before attempting to add it to other square roots.
- Misapplying Coefficient Rules: Mixing up the coefficient rules is another mistake. The coefficient outside the square root should only be added to another coefficient outside a square root of the same radicand. For example, in \( 2\sqrt{x} + 3\sqrt{x} \), you add the coefficients to get \( 5\sqrt{x} \).
- Forgetting to Distribute: When square roots involve expressions with variables, ensure you distribute any multiplication correctly, especially when dealing with expressions like \( a\sqrt{b} + c\sqrt{d} \). For example, \( (2\sqrt{x})(3\sqrt{x}) \) should be correctly calculated as \( 6x \).
- Overcomplicating the Process: Sometimes students overthink the process, leading to unnecessary steps or confusion. Keep the process straightforward: simplify, identify like terms, and then add.
- Ignoring Variable Simplification: When variables are under the square root, they should be simplified just like numerical radicands. For example, \( \sqrt{x^2} \) should be simplified to \( x \) if \( x \) is positive.
By avoiding these common errors, you can improve your ability to work with square roots and variables more accurately and efficiently. Practice with a variety of problems to build your skills and confidence in avoiding these mistakes.
Practice Problems
Practice problems help solidify understanding and improve skills. Try solving the following problems to master adding square roots with variables.
Basic Addition Problems
-
\(\sqrt{18} + \sqrt{8}\)
Solution: Simplify each square root: \(\sqrt{18} = 3\sqrt{2}\), \(\sqrt{8} = 2\sqrt{2}\). Then, add the like terms: \(3\sqrt{2} + 2\sqrt{2} = 5\sqrt{2}\).
-
\(\sqrt{50} + \sqrt{32}\)
Solution: Simplify each square root: \(\sqrt{50} = 5\sqrt{2}\), \(\sqrt{32} = 4\sqrt{2}\). Then, add the like terms: \(5\sqrt{2} + 4\sqrt{2} = 9\sqrt{2}\).
Simplification and Addition
-
\(\sqrt{12} + \sqrt{27}\)
Solution: Simplify each square root: \(\sqrt{12} = 2\sqrt{3}\), \(\sqrt{27} = 3\sqrt{3}\). Then, add the like terms: \(2\sqrt{3} + 3\sqrt{3} = 5\sqrt{3}\).
-
\(2\sqrt{18} + 3\sqrt{8}\)
Solution: Simplify each square root: \(2\sqrt{18} = 2 \cdot 3\sqrt{2} = 6\sqrt{2}\), \(3\sqrt{8} = 3 \cdot 2\sqrt{2} = 6\sqrt{2}\). Then, add the like terms: \(6\sqrt{2} + 6\sqrt{2} = 12\sqrt{2}\).
Advanced Variable Expressions
-
\(\sqrt{50x^2} + \sqrt{8x^2}\)
Solution: Simplify each square root: \(\sqrt{50x^2} = 5x\sqrt{2}\), \(\sqrt{8x^2} = 2x\sqrt{2}\). Then, add the like terms: \(5x\sqrt{2} + 2x\sqrt{2} = 7x\sqrt{2}\).
-
\(3\sqrt{72y^2} + 4\sqrt{18y^2}\)
Solution: Simplify each square root: \(3\sqrt{72y^2} = 3 \cdot 6y\sqrt{2} = 18y\sqrt{2}\), \(4\sqrt{18y^2} = 4 \cdot 3y\sqrt{2} = 12y\sqrt{2}\). Then, add the like terms: \(18y\sqrt{2} + 12y\sqrt{2} = 30y\sqrt{2}\).

Conclusion
Mastering the process of adding square roots with variables is a valuable skill in algebra, which enhances your ability to simplify and solve more complex expressions. Let's summarize the key points and techniques covered in this guide:
- Understanding Like Terms: Recognize that only square roots with the same radicand can be combined. For example, \(3\sqrt{x} + 5\sqrt{x}\) can be added to yield \(8\sqrt{x}\), whereas \(2\sqrt{x} + 3\sqrt{y}\) cannot be combined because the radicands differ.
- Simplification: Always simplify square roots first if possible. This may involve factoring out perfect squares from the radicand and reducing the expression. For instance, \(2\sqrt{8}\) can be simplified to \(4\sqrt{2}\), making it easier to combine with other like terms.
- Combining Like Radicals: Once simplified, add or subtract the coefficients of the like terms while retaining the common radicand. For example, \(4\sqrt{2} + 6\sqrt{2}\) simplifies to \(10\sqrt{2}\).
- Practice Problems: Engage with a variety of problems, starting from basic additions to more complex expressions involving variables. This will strengthen your understanding and ability to apply these concepts efficiently.
- Advanced Techniques: For expressions with different indices or more complex forms, consider transforming the radicals to like terms or applying multiplication before addition to simplify the process.
By consistently practicing and applying these strategies, you can build a strong foundation in handling square roots with variables, paving the way for more advanced mathematical topics. Continue to challenge yourself with diverse problems and seek additional resources or assistance as needed. Happy learning!
Video này hướng dẫn cách rút gọn căn bậc hai có biến số, giúp bạn nắm vững kỹ năng cơ bản trong Toán học.
Rút gọn căn bậc hai với biến số (Đơn giản hóa Toán học)
READ MORE:
Video này hướng dẫn cách cộng và trừ các biểu thức căn bậc hai có biến số, giúp bạn nâng cao kỹ năng trong Toán học.
Cộng và Trừ Biểu thức Căn bậc hai với Biến số (Nâng cao)