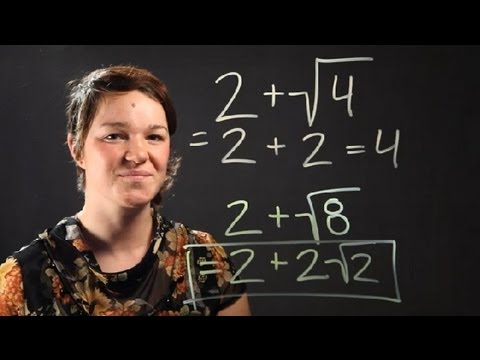Topic adding square roots: Welcome to our comprehensive guide on adding square roots. Whether you're a student or just looking to brush up on your math skills, this article will provide you with clear and easy-to-follow steps, examples, and practice problems to master the art of adding square roots effectively.
Table of Content
- Adding Square Roots
- Introduction to Adding Square Roots
- Step-by-Step Guide to Adding Square Roots
- Examples of Adding Square Roots
- Simplifying Radicals Before Adding
- Combining Like Radicals
- Adding Square Roots with Different Radicands
- Special Cases in Adding Square Roots
- Common Mistakes and How to Avoid Them
- Practice Problems and Solutions
- Applications of Adding Square Roots in Real Life
- Additional Resources and Further Reading
- YOUTUBE: Video hướng dẫn cách thêm và trừ các biểu thức căn bậc hai và căn bậc ba một cách chi tiết và dễ hiểu.
Adding Square Roots
Adding square roots involves specific rules and steps to simplify and combine radical expressions. Below are detailed explanations and examples to help understand the process.
Basic Rules for Adding Square Roots
To add square roots, the radicands (the numbers inside the square root symbols) must be the same. If the radicands are different, the square roots cannot be added directly.
Steps for Adding Square Roots
- Simplify each square root.
- Combine square roots with the same radicand.
Example 1: Adding Simplified Square Roots
Consider the expression \(3\sqrt{5} + 2\sqrt{5}\):
- The radicands are the same (both are \(\sqrt{5}\)).
- Combine the coefficients: \(3 + 2 = 5\).
- The result is \(5\sqrt{5}\).
Example 2: Simplifying Before Adding
Consider the expression \(2\sqrt{12} + \sqrt{27}\):
- Simplify each square root:
- \(2\sqrt{12} = 2\sqrt{4 \times 3} = 2 \times 2\sqrt{3} = 4\sqrt{3}\)
- \(\sqrt{27} = \sqrt{9 \times 3} = 3\sqrt{3}\)
- Now combine the simplified terms: \(4\sqrt{3} + 3\sqrt{3} = 7\sqrt{3}\)
Example 3: Complex Addition
Consider the expression \(\sqrt{18} + 2\sqrt{8}\):
- \(\sqrt{18} = \sqrt{9 \times 2} = 3\sqrt{2}\)
- \(2\sqrt{8} = 2\sqrt{4 \times 2} = 2 \times 2\sqrt{2} = 4\sqrt{2}\)
- Combine the simplified terms: \(3\sqrt{2} + 4\sqrt{2} = 7\sqrt{2}\)
Example 4: Adding Square Roots with Variables
Consider the expression \(5\sqrt{12a} + 2\sqrt{3a}\):
- Simplify the square roots:
- \(5\sqrt{12a} = 5\sqrt{4 \times 3a} = 5 \times 2\sqrt{3a} = 10\sqrt{3a}\)
- \(2\sqrt{3a}\) remains as is.
- Combine the terms: \(10\sqrt{3a} + 2\sqrt{3a} = 12\sqrt{3a}\)
By following these steps, you can simplify and add square roots effectively. Practice with different problems to become proficient in this skill.
Try It Yourself
Try simplifying and adding the following expressions:
- \(\sqrt{20} + \sqrt{45}\)
- \(3\sqrt{32} + 2\sqrt{18}\)
- \(\sqrt{50} + 5\sqrt{2}\)

READ MORE:
Introduction to Adding Square Roots
Adding square roots can seem challenging at first, but with a clear understanding of the basic principles, it becomes much simpler. Square roots are expressions containing a radical symbol (√), and adding them requires combining like terms. In this guide, we'll explore the essential steps and concepts for adding square roots effectively.
- Understanding Square Roots: The square root of a number \( x \) is a value \( y \) such that \( y^2 = x \). For example, \( \sqrt{25} = 5 \) because \( 5^2 = 25 \).
- Like Radicals: To add square roots, the radicands (the numbers under the radical sign) must be the same. For instance, \( \sqrt{3} + \sqrt{3} = 2\sqrt{3} \), but \( \sqrt{3} + \sqrt{5} \) cannot be simplified further.
- Simplifying Radicals: Before adding, simplify the square roots if possible. For example, \( \sqrt{50} \) can be simplified to \( 5\sqrt{2} \), making it easier to combine with other like terms.
Let's delve into the basic rules for adding square roots to build a strong foundation for more complex problems.
Step-by-Step Guide to Adding Square Roots
Adding square roots involves a few straightforward steps. Follow this guide to add square roots accurately:
- Identify Like Radicals
Square roots can only be added if they are like terms, which means they have the same radicand (the number inside the square root). For example, \(\sqrt{5}\) and \(\sqrt{5}\) are like terms, but \(\sqrt{5}\) and \(\sqrt{3}\) are not.
- Simplify the Radicals (if possible)
Before adding, check if the square roots can be simplified. For example, \(\sqrt{18}\) can be simplified to \(3\sqrt{2}\). This step ensures that you are working with the simplest form of each square root.
- Add the Like Radicals
Once you have identified and simplified the like radicals, you can add them together. Combine the coefficients (numbers in front of the square roots) and keep the radical part the same. For example:
- \(\sqrt{5} + 3\sqrt{5} = 4\sqrt{5}\)
- If you have \(2\sqrt{3} + \sqrt{3}\), it combines to \(3\sqrt{3}\).
- Examples
Consider the following examples to illustrate the steps:
- Example 1: \(\sqrt{12} + 2\sqrt{27}\)
- Simplify the radicals: \(\sqrt{12} = 2\sqrt{3}\) and \(2\sqrt{27} = 6\sqrt{3}\)
- Add the like terms: \(2\sqrt{3} + 6\sqrt{3} = 8\sqrt{3}\)
- Example 2: \(\sqrt{8} + \sqrt{2}\)
- Simplify the radicals: \(\sqrt{8} = 2\sqrt{2}\)
- Add the like terms: \(2\sqrt{2} + \sqrt{2} = 3\sqrt{2}\)
- Example 1: \(\sqrt{12} + 2\sqrt{27}\)
- Special Cases
Sometimes, you might encounter square roots that cannot be combined. For instance, \(\sqrt{5} + \sqrt{7}\) cannot be simplified further because the radicands are different and cannot be simplified to like terms.
By following these steps, you can add square roots accurately and efficiently.
Examples of Adding Square Roots
Here are some examples to help illustrate the process of adding square roots:
Example 1: Adding Like Radicals
Consider the following expression:
\[
\sqrt{5} + 2\sqrt{5}
\]
Since both terms have the same radicand (5), they can be combined:
\[
\sqrt{5} + 2\sqrt{5} = 3\sqrt{5}
\]
Example 2: Simplifying Before Adding
Let's add the following square roots:
\[
\sqrt{9} + \sqrt{25}
\]
First, simplify each square root:
\[
\sqrt{9} = 3 \quad \text{and} \quad \sqrt{25} = 5
\]
Now add the simplified values:
\[
3 + 5 = 8
\]
Example 3: Adding Radicals with Different Coefficients
Consider the expression:
\[
3\sqrt{2} + 4\sqrt{2}
\]
Since the radicands are the same (2), combine the coefficients:
\[
(3 + 4)\sqrt{2} = 7\sqrt{2}
\]
Example 4: Simplifying Different Radicands
Consider the following expression:
\[
\sqrt{8} + \sqrt{2}
\]
Simplify \(\sqrt{8}\) first:
\[
\sqrt{8} = \sqrt{4 \times 2} = 2\sqrt{2}
\]
Now add the simplified terms:
\[
2\sqrt{2} + \sqrt{2} = 3\sqrt{2}
\]
Example 5: Complex Addition
Consider the expression:
\[
\sqrt{18} + 2\sqrt{50}
\]
Simplify each square root:
\[
\sqrt{18} = \sqrt{9 \times 2} = 3\sqrt{2}
\]
\[
2\sqrt{50} = 2\sqrt{25 \times 2} = 2 \times 5\sqrt{2} = 10\sqrt{2}
\]
Now add the simplified terms:
\[
3\sqrt{2} + 10\sqrt{2} = 13\sqrt{2}
\]
Example 6: No Simplification Possible
Consider the following expression:
\[
2\sqrt{3} + 3\sqrt{5}
\]
Since the radicands are different and cannot be simplified to have the same radicand, the expression is already in its simplest form:
\[
2\sqrt{3} + 3\sqrt{5}
\]
These terms cannot be combined further.
Simplifying Radicals Before Adding
Simplifying radicals before adding them can make the process much easier and more efficient. Here is a step-by-step guide to simplify radicals before adding:
-
Identify the Radicand: The radicand is the number inside the square root. For example, in \(\sqrt{18}\), 18 is the radicand.
-
Factor the Radicand: Break down the radicand into its prime factors. For instance, 18 can be factored into \(2 \times 3^2\).
-
Apply the Square Root to the Factors: Use the property \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\) to separate the factors. For example, \(\sqrt{18} = \sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2}\).
-
Simplify the Square Roots of Perfect Squares: Any perfect square can be simplified to an integer. For example, \(\sqrt{3^2} = 3\). Thus, \(\sqrt{18} = 3\sqrt{2}\).
-
Repeat for All Terms: Simplify all radicals in the expression. For instance, simplify \(\sqrt{50}\) to \(5\sqrt{2}\) and \(\sqrt{72}\) to \(6\sqrt{2}\).
-
Add the Simplified Radicals: Once all radicals are simplified, combine like terms. For example, if you have \(3\sqrt{2} + 5\sqrt{2} + 6\sqrt{2}\), you can add the coefficients: \(3 + 5 + 6 = 14\). Thus, \(3\sqrt{2} + 5\sqrt{2} + 6\sqrt{2} = 14\sqrt{2}\).
Here's an example to illustrate the process:
-
Simplify and add \(\sqrt{50} + \sqrt{18}\):
- \(\sqrt{50} = \sqrt{2 \times 5^2} = 5\sqrt{2}\)
- \(\sqrt{18} = \sqrt{2 \times 3^2} = 3\sqrt{2}\)
- Add the simplified terms: \(5\sqrt{2} + 3\sqrt{2} = 8\sqrt{2}\)
By following these steps, you can simplify radicals before adding them, making the process straightforward and ensuring accuracy.

Combining Like Radicals
Combining like radicals involves adding or subtracting radicals with the same radicand and index. Here is a detailed, step-by-step guide to combining like radicals:
-
Identify Like Radicals: Ensure that the radicals you want to combine have the same radicand and index. For example, \(3\sqrt{2}\) and \(5\sqrt{2}\) are like radicals, but \(3\sqrt{2}\) and \(5\sqrt{3}\) are not.
-
Simplify the Radicals: If the radicals are not in their simplest form, simplify them first. For example, simplify \(\sqrt{50}\) to \(5\sqrt{2}\).
-
Add or Subtract the Coefficients: Once you have like radicals, add or subtract their coefficients, keeping the radical part unchanged. For instance:
- Example: Combine \(3\sqrt{2}\) and \(5\sqrt{2}\).
- Solution: \[3\sqrt{2} + 5\sqrt{2} = (3+5)\sqrt{2} = 8\sqrt{2}\]
-
Check for Further Simplification: After combining, check if the result can be simplified further.
Here are some examples to illustrate combining like radicals:
-
Example 1: Combine \(2\sqrt{3}\) and \(7\sqrt{3}\).
Solution: \[2\sqrt{3} + 7\sqrt{3} = (2+7)\sqrt{3} = 9\sqrt{3}\]
-
Example 2: Combine \(4\sqrt{5}\) and \(-3\sqrt{5}\).
Solution: \[4\sqrt{5} - 3\sqrt{5} = (4-3)\sqrt{5} = 1\sqrt{5} = \sqrt{5}\]
-
Example 3: Combine \(2\sqrt{7}\), \(5\sqrt{2}\), and \(3\sqrt{7}\).
Solution: Combine like radicals first: \[2\sqrt{7} + 3\sqrt{7} = (2+3)\sqrt{7} = 5\sqrt{7}\]
So, the combined result is: \[5\sqrt{7} + 5\sqrt{2}\]
Since \(5\sqrt{2}\) has a different radicand, it cannot be combined with \(5\sqrt{7}\).
By following these steps, you can effectively combine like radicals to simplify expressions.
Adding Square Roots with Different Radicands
Adding square roots with different radicands can be challenging because, unlike like radicals, you cannot simply combine them directly. Instead, you need to follow a systematic approach to see if they can be simplified to like radicals first. Here’s a step-by-step guide:
-
Identify the Radicands: Determine the radicands (the number inside the square root) of the terms you are trying to add.
-
Check for Simplification: Simplify each square root individually, if possible. This involves factoring the radicand to see if it contains a perfect square.
- For example, \(\sqrt{8}\) can be simplified because 8 can be factored into \(4 \times 2\), and \(\sqrt{4} \times \sqrt{2} = 2\sqrt{2}\).
-
Rewrite the Expression: Rewrite the expression with the simplified square roots. This step helps to identify if any terms now have the same radicand and can be combined.
- For instance, \(\sqrt{2} + \sqrt{8}\) becomes \(\sqrt{2} + 2\sqrt{2}\).
-
Combine Like Radicals: If the simplified terms have the same radicand, you can combine them by adding or subtracting the coefficients.
- Continuing the example, \(\sqrt{2} + 2\sqrt{2}\) becomes \(3\sqrt{2}\).
-
Leave Unlike Radicals: If, after simplification, the terms still have different radicands, they cannot be combined and should be left as they are.
Examples
| \(\sqrt{2} + \sqrt{3}\) | These cannot be combined as the radicands are different. |
| \(\sqrt{18} + \sqrt{8}\) |
Simplify each term: \(\sqrt{18} = 3\sqrt{2}\) and \(\sqrt{8} = 2\sqrt{2}\). Combine like radicals: \(3\sqrt{2} + 2\sqrt{2} = 5\sqrt{2}\). |
| \(\sqrt{50} + \sqrt{2}\) |
Simplify the first term: \(\sqrt{50} = 5\sqrt{2}\). Combine like radicals: \(5\sqrt{2} + \sqrt{2} = 6\sqrt{2}\). |
By following these steps, you can effectively handle adding square roots with different radicands and simplify the expressions when possible.
Special Cases in Adding Square Roots
When adding square roots, special cases often require unique approaches. Below are some common special cases and the steps to handle them:
1. Adding Square Roots with Equal Radicands
If the radicands (the numbers under the square root) are the same, you can add the square roots directly.
- \(\sqrt{a} + \sqrt{a} = 2\sqrt{a}\)
- Example: \(3\sqrt{5} + 2\sqrt{5} = 5\sqrt{5}\)
2. Simplifying Before Adding
When radicands are not the same, try simplifying them first:
- Simplify \(\sqrt{ab}\) to \(\sqrt{a} \cdot \sqrt{b}\)
- Combine like terms if possible.
- Example: \( \sqrt{50} + \sqrt{2} \)
- Simplify \(\sqrt{50}\): \(\sqrt{50} = \sqrt{25 \cdot 2} = 5\sqrt{2}\)
- Now combine: \(5\sqrt{2} + \sqrt{2} = 6\sqrt{2}\)
3. Adding Square Roots with Different Indices
When square roots have different indices, they must be converted to the same index before combining:
- Express roots with fractional exponents.
- Find a common exponent.
- Example: \( \sqrt{2} + \sqrt[3]{4} \)
- Convert to fractional exponents: \(2^{1/2} + 4^{1/3}\)
- Find a common exponent (e.g., 6): \(2^{3/6} + 4^{2/6}\)
- Combine terms if possible.
4. Handling Non-Simplifiable Radicals
In cases where radicals cannot be simplified to like terms, leave them as is:
- Example: \( \sqrt{2} + \sqrt{3} \) cannot be simplified further, so the result is \( \sqrt{2} + \sqrt{3} \).
5. Adding Square Roots Involving Variables
When variables are involved, ensure the radicands are like terms before adding:
- Example: \( \sqrt{2x} + \sqrt{8x} \)
- Simplify \(\sqrt{8x}\): \( \sqrt{8x} = \sqrt{4 \cdot 2x} = 2\sqrt{2x} \)
- Combine: \( \sqrt{2x} + 2\sqrt{2x} = 3\sqrt{2x} \)
Understanding these special cases can help simplify the process of adding square roots and ensure accurate results.
Common Mistakes and How to Avoid Them
When adding square roots, there are several common mistakes that students often make. Understanding these pitfalls and knowing how to avoid them can help you become more proficient at working with square roots. Here are some of the most frequent errors and tips on how to prevent them:
- Failing to Simplify Radicals First
Before attempting to add square roots, make sure to simplify each radical. For example, instead of adding \(\sqrt{8}\) and \(\sqrt{2}\) directly, simplify \(\sqrt{8}\) to \(2\sqrt{2}\). This allows you to combine like terms more easily.
Example:
\(\sqrt{8} + \sqrt{2}\)
Simplify \(\sqrt{8}\): \(2\sqrt{2}\)
Now add: \(2\sqrt{2} + \sqrt{2} = 3\sqrt{2}\)
- Adding Radicals with Different Radicands
Only like radicals, which have the same radicand, can be added. Radicals with different radicands cannot be combined.
Example:
\(\sqrt{3} + \sqrt{5}\)
These cannot be added together because the radicands (3 and 5) are different.
- Ignoring Coefficients
When adding radicals with coefficients, ensure you multiply the coefficients correctly and combine only like radicals.
Example:
\(3\sqrt{2} + 5\sqrt{2}\)
Add the coefficients: \(3 + 5 = 8\)
Result: \(8\sqrt{2}\)
- Mistaking Multiplication for Addition
Remember that adding square roots is different from multiplying them. Ensure you're performing the correct operation.
Example:
\(\sqrt{2} + \sqrt{2} = 2\sqrt{2}\) (Addition)
\(\sqrt{2} \times \sqrt{2} = \sqrt{4} = 2\) (Multiplication)
- Not Rationalizing the Denominator
When dealing with fractions that include square roots, always rationalize the denominator if it contains a radical.
Example:
\(\frac{1}{\sqrt{2}}\)
Multiply numerator and denominator by \(\sqrt{2}\):
\(\frac{\sqrt{2}}{2}\)
By being aware of these common mistakes and practicing regularly, you can improve your skills in adding square roots and avoid these pitfalls.
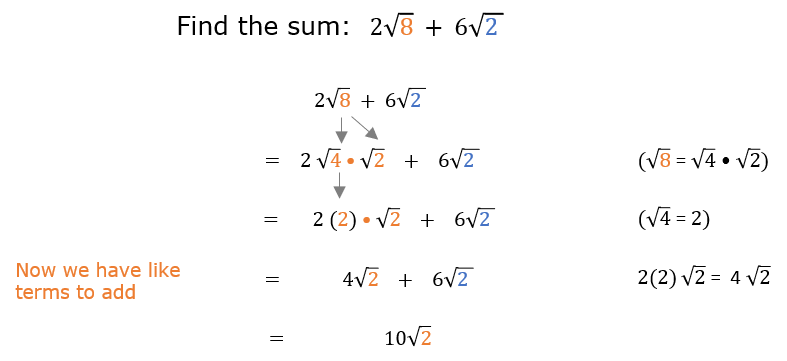
Practice Problems and Solutions
Below are some practice problems and their solutions to help you master adding square roots.
-
Simplify the expression: \(3\sqrt{5} + 6\sqrt{5}\)
Solution: Combine like radicals.
\(3\sqrt{5} + 6\sqrt{5} = (3 + 6)\sqrt{5} = 9\sqrt{5}\)
-
Simplify the expression: \(7\sqrt{3} - 3\sqrt{3}\)
Solution: Combine like radicals.
\(7\sqrt{3} - 3\sqrt{3} = (7 - 3)\sqrt{3} = 4\sqrt{3}\)
-
Simplify the expression: \(5\sqrt{7} + 6\sqrt{7}\)
Solution: Combine like radicals.
\(5\sqrt{7} + 6\sqrt{7} = (5 + 6)\sqrt{7} = 11\sqrt{7}\)
-
Simplify the expression: \(3\sqrt{2} - 7\sqrt{2}\)
Solution: Combine like radicals.
\(3\sqrt{2} - 7\sqrt{2} = (3 - 7)\sqrt{2} = -4\sqrt{2}\)
-
Simplify the expression: \(2\sqrt{5} + 3\sqrt{5} + 4\sqrt{5}\)
Solution: Combine like radicals.
\(2\sqrt{5} + 3\sqrt{5} + 4\sqrt{5} = (2 + 3 + 4)\sqrt{5} = 9\sqrt{5}\)
-
Simplify the expression: \(\sqrt{3} + 4\sqrt{3}\)
Solution: Combine like radicals.
\(\sqrt{3} + 4\sqrt{3} = (1 + 4)\sqrt{3} = 5\sqrt{3}\)
-
Simplify the expression: \(5\sqrt{6} - 3\sqrt{6} + 8\sqrt{6}\)
Solution: Combine like radicals.
\(5\sqrt{6} - 3\sqrt{6} + 8\sqrt{6} = (5 - 3 + 8)\sqrt{6} = 10\sqrt{6}\)
-
Simplify the expression: \(3\sqrt{2} + 5\sqrt{5} + 8\sqrt{2} - 2\sqrt{5}\)
Solution: Combine like radicals.
\(3\sqrt{2} + 8\sqrt{2} + 5\sqrt{5} - 2\sqrt{5} = (3 + 8)\sqrt{2} + (5 - 2)\sqrt{5} = 11\sqrt{2} + 3\sqrt{5}\)
-
Simplify the expression: \(6\sqrt{3} - 3\sqrt{2} + 8\sqrt{3} - \sqrt{2}\)
Solution: Combine like radicals.
\(6\sqrt{3} + 8\sqrt{3} - 3\sqrt{2} - \sqrt{2} = (6 + 8)\sqrt{3} - (3 + 1)\sqrt{2} = 14\sqrt{3} - 4\sqrt{2}\)
-
Simplify the expression: \(2\sqrt{12} + 5\sqrt{27}\)
Solution: Simplify each radical first.
\(2\sqrt{12} + 5\sqrt{27} = 2\sqrt{4 \cdot 3} + 5\sqrt{9 \cdot 3} = 2 \cdot 2\sqrt{3} + 5 \cdot 3\sqrt{3} = 4\sqrt{3} + 15\sqrt{3} = 19\sqrt{3}\)
-
Simplify the expression: \(5\sqrt{3} - \sqrt{27}\)
Solution: Simplify each radical first.
\(5\sqrt{3} - \sqrt{27} = 5\sqrt{3} - \sqrt{9 \cdot 3} = 5\sqrt{3} - 3\sqrt{3} = (5 - 3)\sqrt{3} = 2\sqrt{3}\)
-
Simplify the expression: \(\sqrt{30} + \sqrt{5}\)
Solution: Since the radicands are different and cannot be simplified to have the same radicand, the expression remains as it is.
\(\sqrt{30} + \sqrt{5}\)
Applications of Adding Square Roots in Real Life
Square roots play a significant role in various real-life applications across different fields. Here are some notable examples:
-
Geometry and Architecture:
In geometry, square roots are essential for calculating distances and lengths. For example, the Pythagorean theorem, which involves square roots, is used to determine the length of the hypotenuse of a right triangle. Architects use these calculations to ensure the structural integrity of buildings and bridges.
Example:
If a right triangle has legs of length 3 and 4 units, the hypotenuse can be found using the formula:
\( \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \) units
-
Physics and Engineering:
Square roots are used in various physics formulas, such as those calculating velocity, acceleration, and force. Engineers also use square roots in formulas for designing mechanical systems and analyzing stress and strain in materials.
Example:
To find the velocity \( v \) of an object under constant acceleration \( a \) over a distance \( d \), the formula \( v = \sqrt{2ad} \) is used.
-
Finance:
In finance, square roots are used to calculate standard deviation, a measure of volatility or risk in investment returns. This helps investors assess the risk associated with a particular investment.
Example:
If the variance of an investment's returns is 25, the standard deviation is \( \sqrt{25} = 5 \).
-
Statistics:
Statisticians use square roots to calculate the standard deviation, which indicates how much individual data points deviate from the mean. This is crucial for data analysis and interpretation.
Example:
Given a variance \( \sigma^2 \) of 16, the standard deviation \( \sigma \) is \( \sqrt{16} = 4 \).
-
Computer Science:
In computer graphics, square roots are used to calculate distances between points in 2D and 3D spaces. This is fundamental in rendering graphics and animations.
Example:
The distance \( D \) between two points \((x_1, y_1)\) and \((x_2, y_2)\) is calculated using \( D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \).
Additional Resources and Further Reading
For those looking to deepen their understanding of adding square roots, the following resources provide comprehensive explanations, examples, and practice problems:
For those interested in textbooks and reference books, consider the following:
| Title | Author | Details |
| Richard G. Brown | A comprehensive textbook covering algebraic concepts including radicals. | |
| Ron Larson, Laurie Boswell, Timothy D. Kanold, Lee Stiff | This book provides foundational knowledge in algebra, including operations with radicals. | |
| Marvin L. Bittinger, David J. Ellenbogen, Barbara L. Johnson | An in-depth guide that includes intermediate algebra topics, such as combining and simplifying radicals. |
Additionally, online forums and study groups can be valuable resources for further learning and problem-solving:
Exploring these resources will help you gain a more thorough understanding of adding square roots and their applications in various mathematical contexts.
Video hướng dẫn cách thêm và trừ các biểu thức căn bậc hai và căn bậc ba một cách chi tiết và dễ hiểu.
Thêm và Trừ Các Biểu Thức Căn Bậc Hai và Căn Bậc Ba
READ MORE:
Video hướng dẫn chi tiết về cách thêm và trừ các biểu thức căn bậc hai, giúp người học hiểu rõ và nắm vững kiến thức.
Thêm và Trừ Căn Bậc Hai