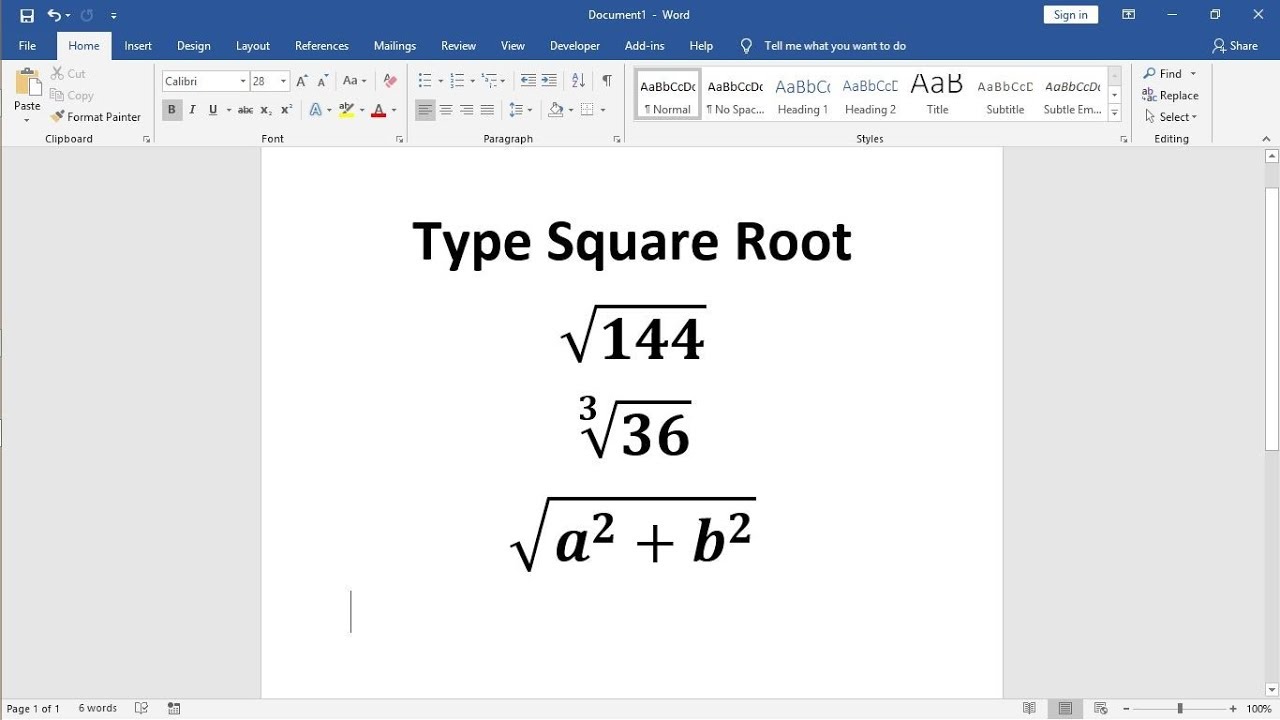
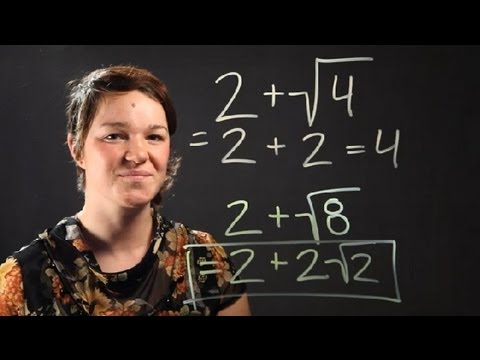Topic adding square roots rules: Discover the essential rules for adding square roots in this comprehensive guide. Simplify your calculations and enhance your mathematical skills with clear explanations and practical examples. Whether you're a student or a math enthusiast, this article will help you master the art of combining square roots effortlessly and accurately.
Table of Content
- Adding Square Roots Rules
- Introduction to Square Roots
- Basic Properties of Square Roots
- Understanding the Concept of Adding Square Roots
- Rules for Adding Square Roots
- Combining Like Terms
- Simplifying Square Roots Before Addition
- Step-by-Step Guide to Adding Square Roots
- Examples and Practice Problems
- Common Mistakes and How to Avoid Them
- Advanced Techniques for Adding Square Roots
- Real-World Applications of Adding Square Roots
- Conclusion and Summary
- YOUTUBE: Hướng dẫn cách cộng và trừ căn bậc hai, giúp bạn nắm vững quy tắc và kỹ thuật thực hiện phép tính với căn bậc hai.
Adding Square Roots Rules
Adding square roots involves combining terms with the same radicand (the number inside the square root). If the radicands are different, the terms cannot be directly added together. Below are the detailed steps and rules for adding square roots:
Steps to Add Square Roots
- Identify Like Terms: Check if the square roots have the same radicand. For example,
\(\sqrt{2}\) and \(\sqrt{2}\) are like terms, but\(\sqrt{2}\) and \(\sqrt{3}\) are not. - Combine Coefficients: Add or subtract the coefficients of the like terms. For example,
\(2\sqrt{2} + 3\sqrt{2} = 5\sqrt{2}\) . - Simplify if Necessary: If the square roots can be simplified, do so before adding. For instance,
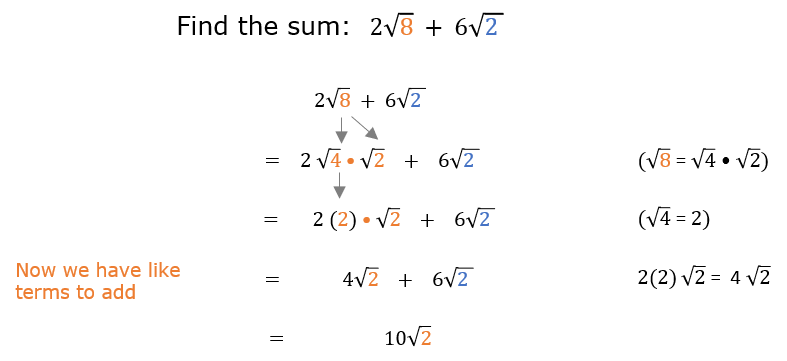
\(\sqrt{50} + \sqrt{18}\) simplifies to\(5\sqrt{2} + 3\sqrt{2} = 8\sqrt{2}\) .
Examples
Example 1: Add
\(3\sqrt{5}\) and \(4\sqrt{5}\) :\(3\sqrt{5} + 4\sqrt{5} = 7\sqrt{5}\) Example 2: Add
\(2\sqrt{7}\) and \(5\sqrt{3}\) :These terms cannot be combined as they have different radicands.
Example 3: Simplify and add
\(2\sqrt{8}\) and \(3\sqrt{2}\) :\(2\sqrt{8} = 2 \times 2\sqrt{2} = 4\sqrt{2}\) , then\(4\sqrt{2} + 3\sqrt{2} = 7\sqrt{2}\) .
Important Notes
- You can only combine square roots with the same radicand.
- Always simplify the square roots first before adding them.
- If the radicands are different, the terms remain separate in the expression.
Practice Problems
- Simplify:
\(5\sqrt{3} + 2\sqrt{3}\) - Simplify:
\(\sqrt{18} + \sqrt{2}\) - Add after simplifying:
\(3\sqrt{50} + 2\sqrt{8}\)
Remember, the key to adding square roots is to look for like terms and simplify where possible. Practice these steps to master the concept!
READ MORE:
Introduction to Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. It is denoted by the radical symbol √. For example, the square root of 16 is 4, because \(4 \times 4 = 16\).
Square roots are fundamental in various areas of mathematics and are essential for solving quadratic equations, understanding geometric properties, and more. Below are some key properties and definitions to get you started:
- Positive and Negative Roots: Every positive number has two square roots: one positive and one negative. For instance, the square roots of 25 are 5 and -5.
- Principal Square Root: The non-negative square root of a number is known as the principal square root. It is typically what we refer to when we mention the square root without further qualification.
- Square Root of Zero: The square root of zero is zero.
- No Real Square Root for Negative Numbers: Negative numbers do not have real square roots. However, they have complex square roots involving the imaginary unit \(i\), where \(i^2 = -1\).
Here are some basic examples:
| Number | Square Root |
|---|---|
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
Understanding square roots is crucial before moving on to more complex operations like adding them. In the next section, we will delve deeper into the rules and techniques for adding square roots effectively.
Basic Properties of Square Roots
Square roots possess several fundamental properties that make them useful in various mathematical contexts. Understanding these properties is essential for simplifying and manipulating expressions involving square roots. Here are the key properties:
- Non-Negativity: The principal square root of a non-negative number is always non-negative. For any non-negative number \(a\), \( \sqrt{a} \geq 0 \).
- Product Property: The square root of a product is the product of the square roots. Mathematically, for any non-negative numbers \(a\) and \(b\), \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \).
- Quotient Property: The square root of a quotient is the quotient of the square roots. For any non-negative numbers \(a\) and \(b\) (with \(b \neq 0\)), \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \).
- Square of a Square Root: The square of a square root returns the original number. For any non-negative number \(a\), \( (\sqrt{a})^2 = a \).
- Additive Property: The square root of a sum is not generally equal to the sum of the square roots. For example, \( \sqrt{a + b} \neq \sqrt{a} + \sqrt{b} \) unless \(a\) or \(b\) is zero.
- Square Roots and Exponents: The square root of a number can be expressed as an exponent. For any non-negative number \(a\), \( \sqrt{a} = a^{\frac{1}{2}} \).
Below are some examples demonstrating these properties:
| Property | Example | Explanation |
|---|---|---|
| Non-Negativity | \( \sqrt{9} = 3 \) | The principal square root of 9 is 3, which is non-negative. |
| Product Property | \( \sqrt{4 \cdot 9} = \sqrt{36} = 6 \) | \( \sqrt{4} \cdot \sqrt{9} = 2 \cdot 3 = 6 \) |
| Quotient Property | \( \sqrt{\frac{16}{4}} = \sqrt{4} = 2 \) | \( \frac{\sqrt{16}}{\sqrt{4}} = \frac{4}{2} = 2 \) |
| Square of a Square Root | \( (\sqrt{5})^2 = 5 \) | Squaring the square root of 5 returns the original number 5. |
| Additive Property | \( \sqrt{4 + 9} = \sqrt{13} \neq \sqrt{4} + \sqrt{9} = 2 + 3 = 5 \) | The square root of a sum is not the same as the sum of the square roots. |
| Square Roots and Exponents | \( \sqrt{25} = 25^{\frac{1}{2}} = 5 \) | The square root of 25 expressed as an exponent is 5. |
These basic properties form the foundation for more complex operations involving square roots, such as addition, which we will explore in the next sections.
Understanding the Concept of Adding Square Roots
Adding square roots is a fundamental operation in algebra, but it requires understanding and applying specific rules to combine them correctly. Unlike regular addition, you cannot simply add the numbers under the square root symbols unless certain conditions are met. Here’s a step-by-step guide to understanding the concept:
- Identifying Like Terms:
Like terms are square roots that have the same radicand (the number under the square root symbol). Only like terms can be added directly. For example, \( \sqrt{3} + \sqrt{3} \) can be added because the radicand is the same (3).
- Combining Like Terms:
When you have like terms, you can add them by adding the coefficients (the numbers in front of the square roots). For instance:
\( 2\sqrt{5} + 3\sqrt{5} = (2 + 3)\sqrt{5} = 5\sqrt{5} \)
- Simplifying Square Roots:
If the square roots are not like terms, you may need to simplify them first. Simplifying square roots involves finding the prime factorization of the radicand and reducing it. For example:
\( \sqrt{50} = \sqrt{25 \cdot 2} = 5\sqrt{2} \)
- Checking for Like Terms After Simplification:
After simplifying, check if the square roots now have the same radicand. If they do, you can combine them. For example:
\( \sqrt{18} + \sqrt{8} = \sqrt{9 \cdot 2} + \sqrt{4 \cdot 2} = 3\sqrt{2} + 2\sqrt{2} = (3 + 2)\sqrt{2} = 5\sqrt{2} \)
Here’s a table summarizing the process:
| Step | Action | Example |
|---|---|---|
| 1 | Identify Like Terms | \( \sqrt{3} + \sqrt{3} \) |
| 2 | Combine Like Terms | \( 2\sqrt{5} + 3\sqrt{5} = 5\sqrt{5} \) |
| 3 | Simplify Square Roots | \( \sqrt{50} = 5\sqrt{2} \) |
| 4 | Check for Like Terms After Simplification | \( \sqrt{18} + \sqrt{8} = 5\sqrt{2} \) |
By following these steps, you can accurately add square roots and simplify your mathematical expressions. Practice these methods to become more proficient in handling square root operations.
Rules for Adding Square Roots
Adding square roots involves specific rules to ensure accurate calculations. These rules help simplify the process and prevent common errors. Here are the detailed rules for adding square roots:
- Identify Like Terms:
Like terms are square roots that have the same radicand. Only like terms can be added directly. For example, \( \sqrt{7} \) and \( 2\sqrt{7} \) are like terms because they both contain \( \sqrt{7} \).
- Combine Like Terms:
Add the coefficients of like terms while keeping the radicand the same. For instance:
\( 3\sqrt{2} + 4\sqrt{2} = (3 + 4)\sqrt{2} = 7\sqrt{2} \)
- Simplify Before Adding:
If the terms are not like terms initially, simplify the square roots first. This may involve breaking down the radicand into its prime factors and simplifying. For example:
\( \sqrt{50} = \sqrt{25 \cdot 2} = 5\sqrt{2} \)
- Check for Like Terms After Simplification:
After simplifying the square roots, check if they are now like terms. If they are, combine them. For example:
\( \sqrt{18} + \sqrt{8} = \sqrt{9 \cdot 2} + \sqrt{4 \cdot 2} = 3\sqrt{2} + 2\sqrt{2} = (3 + 2)\sqrt{2} = 5\sqrt{2} \)
- Adding Unlike Terms:
If the square roots cannot be simplified to like terms, they cannot be added directly. For instance:
\( \sqrt{5} + \sqrt{3} \) cannot be combined because the radicands are different.
Below is a summary table to illustrate these rules:
| Step | Action | Example |
|---|---|---|
| 1 | Identify Like Terms | \( \sqrt{7} + 2\sqrt{7} \) |
| 2 | Combine Like Terms | \( 3\sqrt{2} + 4\sqrt{2} = 7\sqrt{2} \) |
| 3 | Simplify Before Adding | \( \sqrt{50} = 5\sqrt{2} \) |
| 4 | Check for Like Terms After Simplification | \( \sqrt{18} + \sqrt{8} = 5\sqrt{2} \) |
| 5 | Adding Unlike Terms | \( \sqrt{5} + \sqrt{3} \) cannot be combined |
By following these rules, you can add square roots accurately and simplify complex mathematical expressions with confidence.

Combining Like Terms
Combining like terms is a crucial step in simplifying expressions involving square roots. Like terms are square roots that share the same radicand. Here’s a detailed guide on how to combine like terms effectively:
- Identify Like Terms:
Like terms have the same number under the square root symbol. For example, \( \sqrt{3} \) and \( 2\sqrt{3} \) are like terms because both contain \( \sqrt{3} \). On the other hand, \( \sqrt{3} \) and \( \sqrt{5} \) are not like terms because their radicands are different.
- Check the Coefficients:
Once you’ve identified the like terms, look at their coefficients. The coefficients are the numbers in front of the square root symbol. For example, in \( 3\sqrt{7} + 2\sqrt{7} \), the coefficients are 3 and 2, respectively.
- Add the Coefficients:
To combine the like terms, add their coefficients together while keeping the radicand the same. For instance:
\( 3\sqrt{2} + 4\sqrt{2} = (3 + 4)\sqrt{2} = 7\sqrt{2} \)
- Write the Result:
After adding the coefficients, write the result as a single term. For example, combining \( 5\sqrt{3} \) and \( 6\sqrt{3} \) results in:
\( 5\sqrt{3} + 6\sqrt{3} = 11\sqrt{3} \)
- Simplify Further if Possible:
If the resulting term can be simplified further, do so. However, if the term is already in its simplest form, you are done. For instance, \( 8\sqrt{2} \) cannot be simplified further.
Here’s a table to summarize the steps:
| Step | Action | Example |
|---|---|---|
| 1 | Identify Like Terms | \( \sqrt{5} \) and \( 3\sqrt{5} \) |
| 2 | Check the Coefficients | Coefficients: 1 and 3 |
| 3 | Add the Coefficients | \( \sqrt{5} + 3\sqrt{5} = 4\sqrt{5} \) |
| 4 | Write the Result | \( 4\sqrt{5} \) |
| 5 | Simplify Further if Possible | \( 4\sqrt{5} \) (Already simplified) |
By following these steps, you can easily combine like terms involving square roots and simplify your expressions for more manageable calculations.
Simplifying Square Roots Before Addition
Before adding square roots, it's often necessary to simplify them to ensure accurate calculations. Simplifying square roots involves expressing the radicand in its simplest form, which can help in identifying like terms. Here’s a detailed, step-by-step guide on how to simplify square roots before addition:
- Find the Prime Factorization:
Break down the number under the square root (the radicand) into its prime factors. For example:
\( 72 = 2 \times 2 \times 2 \times 3 \times 3 \)
- Pair the Prime Factors:
Group the prime factors into pairs. Each pair of identical factors can be simplified as a single factor outside the square root. For example:
\( \sqrt{72} = \sqrt{2 \times 2 \times 2 \times 3 \times 3} = \sqrt{(2 \times 2) \times 2 \times (3 \times 3)} \)
- Simplify the Pairs:
Move each pair of prime factors outside the square root as a single factor. For example:
\( \sqrt{72} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2} \)
- Repeat for Each Term:
If you have multiple square roots to add, repeat the simplification process for each term. For instance:
\( \sqrt{50} = \sqrt{25 \times 2} = 5\sqrt{2} \)
\( \sqrt{18} = \sqrt{9 \times 2} = 3\sqrt{2} \)
- Combine Like Terms:
After simplifying, check if the square roots have the same radicand. If they do, you can combine them by adding their coefficients. For example:
\( 5\sqrt{2} + 3\sqrt{2} = (5 + 3)\sqrt{2} = 8\sqrt{2} \)
Here’s a table summarizing the process:
| Step | Action | Example |
|---|---|---|
| 1 | Find the Prime Factorization | \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \) |
| 2 | Pair the Prime Factors | \( \sqrt{72} = \sqrt{(2 \times 2) \times 2 \times (3 \times 3)} \) |
| 3 | Simplify the Pairs | \( \sqrt{72} = 6\sqrt{2} \) |
| 4 | Repeat for Each Term | \( \sqrt{50} = 5\sqrt{2} \) and \( \sqrt{18} = 3\sqrt{2} \) |
| 5 | Combine Like Terms | \( 5\sqrt{2} + 3\sqrt{2} = 8\sqrt{2} \) |
By following these steps, you can simplify square roots effectively before adding them, ensuring that your calculations are accurate and your expressions are simplified.
Step-by-Step Guide to Adding Square Roots
Adding square roots can seem challenging at first, but by following a systematic approach, you can simplify the process and ensure accurate results. Here is a detailed, step-by-step guide to adding square roots:
- Identify the Square Roots to be Added:
Start by listing the square roots you need to add. For example:
\( \sqrt{18} + \sqrt{8} \)
- Simplify Each Square Root:
Simplify each square root by expressing the radicand in its prime factors and then simplifying. For instance:
\( \sqrt{18} = \sqrt{9 \times 2} = 3\sqrt{2} \)
\( \sqrt{8} = \sqrt{4 \times 2} = 2\sqrt{2} \)
- Identify Like Terms:
Check if the simplified square roots have the same radicand. In this example, both \( 3\sqrt{2} \) and \( 2\sqrt{2} \) have the same radicand (\( \sqrt{2} \)), making them like terms.
- Combine Like Terms:
Add the coefficients of the like terms while keeping the radicand the same. For example:
\( 3\sqrt{2} + 2\sqrt{2} = (3 + 2)\sqrt{2} = 5\sqrt{2} \)
- Write the Final Result:
After combining the like terms, write the final result. For this example, the result is:
\( \sqrt{18} + \sqrt{8} = 5\sqrt{2} \)
Here’s a summary table of the process:
| Step | Action | Example |
|---|---|---|
| 1 | Identify the Square Roots | \( \sqrt{18} + \sqrt{8} \) |
| 2 | Simplify Each Square Root | \( \sqrt{18} = 3\sqrt{2} \), \( \sqrt{8} = 2\sqrt{2} \) |
| 3 | Identify Like Terms | \( 3\sqrt{2} \) and \( 2\sqrt{2} \) |
| 4 | Combine Like Terms | \( 3\sqrt{2} + 2\sqrt{2} = 5\sqrt{2} \) |
| 5 | Write the Final Result | \( 5\sqrt{2} \) |
By following this step-by-step guide, you can confidently add square roots and simplify your expressions efficiently. Practice these steps with different problems to become more comfortable with the process.
Examples and Practice Problems
Practicing the addition of square roots can help reinforce your understanding and build confidence. Below are some examples followed by practice problems to help you master adding square roots.
Examples
- Example 1:
Simplify and add \( \sqrt{50} + \sqrt{18} \).
- Simplify each square root:
- Combine like terms:
- Final result:
\( \sqrt{50} = \sqrt{25 \times 2} = 5\sqrt{2} \)
\( \sqrt{18} = \sqrt{9 \times 2} = 3\sqrt{2} \)
\( 5\sqrt{2} + 3\sqrt{2} = (5 + 3)\sqrt{2} = 8\sqrt{2} \)
\( \sqrt{50} + \sqrt{18} = 8\sqrt{2} \)
- Example 2:
Add \( 2\sqrt{3} + 4\sqrt{3} \).
- Identify like terms:
- Combine the coefficients:
- Final result:
Both terms have the same radicand (\( \sqrt{3} \)).
\( 2\sqrt{3} + 4\sqrt{3} = (2 + 4)\sqrt{3} = 6\sqrt{3} \)
\( 2\sqrt{3} + 4\sqrt{3} = 6\sqrt{3} \)
- Example 3:
Simplify and add \( \sqrt{32} + \sqrt{18} \).
- Simplify each square root:
- Combine like terms:
- Final result:
\( \sqrt{32} = \sqrt{16 \times 2} = 4\sqrt{2} \)
\( \sqrt{18} = \sqrt{9 \times 2} = 3\sqrt{2} \)
\( 4\sqrt{2} + 3\sqrt{2} = (4 + 3)\sqrt{2} = 7\sqrt{2} \)
\( \sqrt{32} + \sqrt{18} = 7\sqrt{2} \)
Practice Problems
Try solving these practice problems on your own. Simplify each square root and add the like terms:
- Simplify and add \( \sqrt{72} + \sqrt{18} \).
- Add \( 3\sqrt{5} + 7\sqrt{5} \).
- Simplify and add \( \sqrt{45} + \sqrt{20} \).
- Add \( 2\sqrt{7} + 5\sqrt{7} \).
- Simplify and add \( \sqrt{12} + \sqrt{27} \).
Check your answers:
- \( \sqrt{72} + \sqrt{18} = 6\sqrt{2} + 3\sqrt{2} = 9\sqrt{2} \)
- \( 3\sqrt{5} + 7\sqrt{5} = 10\sqrt{5} \)
- \( \sqrt{45} + \sqrt{20} = 3\sqrt{5} + 2\sqrt{5} = 5\sqrt{5} \)
- \( 2\sqrt{7} + 5\sqrt{7} = 7\sqrt{7} \)
- \( \sqrt{12} + \sqrt{27} = 2\sqrt{3} + 3\sqrt{3} = 5\sqrt{3} \)
By working through these examples and practice problems, you’ll gain a deeper understanding of how to add square roots effectively.

Common Mistakes and How to Avoid Them
Adding square roots can be tricky, and there are several common mistakes that students often make. Here, we'll outline these mistakes and provide tips on how to avoid them.
1. Not Simplifying Radicals Before Adding
One of the most common mistakes is not simplifying the square roots before attempting to add them. Simplifying can reveal like terms that can be combined. Follow these steps:
- Identify the largest perfect square factor of each radicand.
- Rewrite the square root as a product of the square root of the perfect square and the square root of the remaining factor.
- Simplify the expression.
For example:
√24 + 5√54 + √96 = 2√6 + 15√6 + 4√6 = (2 + 15 + 4)√6 = 21√6
2. Combining Unlike Terms
Square roots can only be added if they have the same radicand. Combining square roots with different radicands is incorrect.
Correct approach:
√3 + √12 ≠ √15 √3 + √12 = √3 + 2√3 = 3√3
3. Ignoring Coefficients
When adding square roots, it's important to correctly handle the coefficients. Only the coefficients of like terms should be added.
2√5 + 3√5 = (2 + 3)√5 = 5√5
4. Incorrect Simplification of Radicals
Ensure proper simplification of radicals. Mistakes in this step can lead to incorrect results.
√50 = √(25 * 2) = 5√2
5. Forgetting to Check for Further Simplification
After combining like terms, check if the result can be simplified further.
3√18 = 3√(9 * 2) = 3 * 3√2 = 9√2
6. Mistaking Addition for Multiplication Rules
Do not apply multiplication rules to addition. Adding square roots is not the same as multiplying them.
√3 + √3 = 2√3 √3 * √3 = 3
7. Misinterpreting the Radicand
Ensure you correctly identify the radicand (the number inside the square root). Mistaking this can lead to incorrect operations.
Example:
√(2 * 8) = √16 = 4 √2 * √8 = √16 = 4
By avoiding these common mistakes and carefully following the rules for adding square roots, you can accurately solve problems involving radical expressions.
Advanced Techniques for Adding Square Roots
Adding square roots can become more complex when dealing with different radicands or coefficients. Here are some advanced techniques to handle such scenarios efficiently.
Simplifying Square Roots
Before adding square roots, simplify them as much as possible. This often involves factoring out perfect squares from the radicand:
- For example, simplify \( 2\sqrt{20} \) to \( 4\sqrt{5} \) by factoring out the square root of 4.
- Similarly, simplify \( 3\sqrt{45} \) to \( 9\sqrt{5} \) by factoring out the square root of 9.
Once simplified, you can easily add the square roots if they have like terms:
\( 4\sqrt{5} + 9\sqrt{5} = 13\sqrt{5} \)
Combining Like Radicals
To combine square roots, they must have the same radicand:
- Identify like radicals, such as \( \sqrt{3} \) and \( 2\sqrt{3} \).
- Add or subtract the coefficients while keeping the radicand unchanged: \( \sqrt{3} + 2\sqrt{3} = 3\sqrt{3} \).
Handling Different Radicands
When square roots have different radicands, you need to simplify them to check if they can be made alike:
- Simplify \( 2\sqrt{8} \) to \( 4\sqrt{2} \).
- Identify that \( 3\sqrt{2} \) can be combined with \( 4\sqrt{2} \).
- Add the coefficients: \( 4\sqrt{2} + 3\sqrt{2} = 7\sqrt{2} \).
Advanced Example
Consider adding \( 2\sqrt{50} \) and \( 3\sqrt{18} \):
- Simplify \( 2\sqrt{50} \) to \( 10\sqrt{2} \).
- Simplify \( 3\sqrt{18} \) to \( 9\sqrt{2} \).
- Combine the like terms: \( 10\sqrt{2} + 9\sqrt{2} = 19\sqrt{2} \).
Rationalizing the Denominator
When adding square roots that involve fractions, rationalize the denominator to simplify the expression:
- Identify the denominator, such as in \( \frac{1}{\sqrt{5}} \).
- Multiply both numerator and denominator by the same radical: \( \frac{1}{\sqrt{5}} \times \frac{\sqrt{5}}{\sqrt{5}} = \frac{\sqrt{5}}{5} \).
Using these advanced techniques ensures that you can handle more complex square root addition problems effectively. Always simplify where possible and combine like terms to achieve the most simplified form of your expression.
Real-World Applications of Adding Square Roots
Adding square roots is not just a mathematical exercise; it has practical applications in various fields. Understanding these applications can enhance comprehension and appreciation of this mathematical concept. Here are some real-world examples where adding square roots is essential:
- Architecture and Engineering:
In architecture, square roots are used to calculate various dimensions and support structures. For instance, when determining the length of diagonal supports or the natural frequency of a structure, architects and engineers often add or manipulate square roots.
- Finance:
In the financial world, square roots are used to calculate standard deviations and variances, which are critical in assessing investment risks. Adding square roots helps in complex risk management and in determining the volatility of stock prices.
- Physics:
In physics, adding square roots is essential for calculations involving distances, velocities, and accelerations. For example, when calculating the resultant vector of forces acting at different angles, the Pythagorean theorem, which involves adding square roots, is frequently used.
- Statistics:
Statisticians use square roots when calculating the standard deviation and variance of data sets. Adding these values helps in understanding data distribution and variability, which is crucial in data analysis and prediction models.
- Navigation and Geography:
Square roots are used in navigation to compute distances between points. Pilots and sailors add square roots to calculate the shortest path between two locations on the Earth's surface, using the haversine formula for accurate distance measurement.
- Computer Science:
In computer graphics and cryptography, adding square roots is often necessary. For instance, when calculating distances between pixels or generating encryption keys, algorithms frequently incorporate the addition of square roots.
Understanding these applications not only highlights the importance of mastering the concept of adding square roots but also shows how intertwined mathematics is with our daily lives and professional fields.
Conclusion and Summary
In conclusion, adding square roots is a valuable mathematical skill that is applicable in various fields, from engineering to physics. By understanding the basic properties and rules of square roots, you can simplify and add them accurately. Here is a summary of the key points discussed in this guide:
- Understanding Square Roots: Square roots are numbers that, when multiplied by themselves, yield the original number.
- Basic Properties: Square roots follow properties such as \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\) and \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\).
- Adding Square Roots: To add square roots, the radicands (the numbers under the square root) must be the same. For example, \(\sqrt{3} + 2\sqrt{3} = 3\sqrt{3}\).
- Simplifying Radicals: Before adding, simplify square roots by factoring out squares. For instance, \(\sqrt{50} = \sqrt{25 \times 2} = 5\sqrt{2}\).
- Combining Like Terms: Combine square roots that have the same radicand. For example, \(3\sqrt{5} + 4\sqrt{5} = 7\sqrt{5}\).
- Common Mistakes: Avoid combining square roots with different radicands and always simplify square roots before adding.
- Advanced Techniques: Use algebraic manipulation and properties of square roots to handle more complex expressions.
- Real-World Applications: Adding square roots is used in calculations involving distances, areas, and physical phenomena where square relationships are present.
By following these guidelines and practicing regularly, you can master the addition of square roots and apply this knowledge effectively in both academic and real-world scenarios.
Hướng dẫn cách cộng và trừ căn bậc hai, giúp bạn nắm vững quy tắc và kỹ thuật thực hiện phép tính với căn bậc hai.
Cách Cộng và Trừ Căn Bậc Hai
READ MORE:
Hướng dẫn cách cộng và trừ biểu thức căn bậc hai và căn bậc ba, giúp bạn nắm vững quy tắc và kỹ thuật thực hiện phép tính với căn số.
Cộng và Trừ Biểu Thức Căn Bậc Hai và Căn Bậc Ba