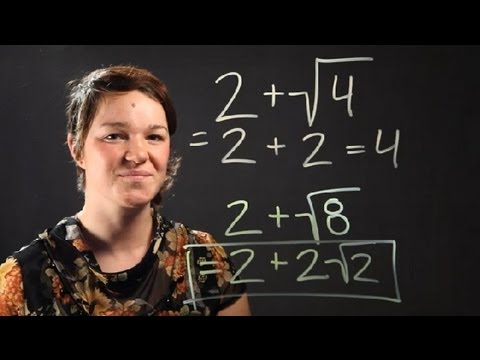Topic adding two square roots: Adding two square roots can seem challenging at first, but with the right techniques, it becomes a straightforward process. In this article, you'll learn how to simplify and add square roots, identify like terms, and avoid common mistakes. Whether you're a student or a math enthusiast, this guide will help you master adding two square roots with confidence.
Table of Content
- Adding Two Square Roots
- Introduction to Square Roots
- Basics of Adding Square Roots
- Identifying Like Terms in Square Roots
- Steps to Simplify Square Roots
- Adding Like Square Roots
- Combining Unlike Square Roots
- Examples of Adding Square Roots
- Common Mistakes and How to Avoid Them
- Practice Problems and Solutions
- Advanced Techniques in Adding Square Roots
- Applications of Adding Square Roots
- Conclusion
- YOUTUBE: Hướng dẫn cách thêm và trừ biểu thức căn bậc hai và căn bậc ba một cách chi tiết và dễ hiểu. Phù hợp cho người học ở mọi cấp độ.
Adding Two Square Roots
Adding two square roots involves combining radical terms, which can be done if the terms are like radicals. Here's a detailed guide on how to perform this operation.
Basic Concept
To add two square roots, the radicands (the numbers inside the square root symbol) must be the same. If they are not, you must simplify them first to see if they can be made alike.
Steps for Adding Square Roots
- Simplify each square root
- Find the prime factors of the number inside the square root.
- Pair the prime factors and move them outside the square root.
- Combine like terms
- If the simplified forms of the square roots have the same radicand, you can add the coefficients (numbers in front of the square roots).
- If the radicands are different, the terms cannot be combined.
Examples
| Expression | Steps | Result |
|---|---|---|
| \(\sqrt{18} + \sqrt{8}\) |
|
\(5\sqrt{2}\) |
| \(\sqrt{50} + \sqrt{2}\) |
|
\(6\sqrt{2}\) |
| \(\sqrt{12} + \sqrt{27}\) |
|
\(5\sqrt{3}\) |
Practice Problems
- Simplify and add: \(\sqrt{32} + \sqrt{18}\)
- Simplify and add: \(\sqrt{75} + \sqrt{12}\)
- Simplify and add: \(\sqrt{45} + \sqrt{20}\)
By following these steps and practicing with the examples, you'll become proficient in adding square roots.

READ MORE:
Introduction to Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3 because \(3 \times 3 = 9\). Square roots are often represented using the radical symbol \( \sqrt{} \).
Key properties of square roots include:
- The square root of a positive number is always positive.
- \(\sqrt{a^2} = a\) for any non-negative number \(a\).
- \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\).
- \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\).
Here is a table of common square roots:
| \(\sqrt{1}\) | 1 |
| \(\sqrt{4}\) | 2 |
| \(\sqrt{9}\) | 3 |
| \(\sqrt{16}\) | 4 |
| \(\sqrt{25}\) | 5 |
Understanding these basics will help you as we explore how to add two square roots effectively.
Basics of Adding Square Roots
Adding square roots involves simplifying the radicals and combining like terms. The process can be broken down into the following steps:
-
Simplify each square root: Break down the number under the square root into its prime factors and simplify. For example:
\(\sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} = 3\sqrt{2}\)
-
Identify like terms: Like terms in square roots have the same radical part. For instance, \(3\sqrt{2}\) and \(5\sqrt{2}\) are like terms, while \(3\sqrt{2}\) and \(4\sqrt{3}\) are not.
-
Add like terms: Combine the coefficients of the like terms. For example:
\(3\sqrt{2} + 5\sqrt{2} = (3 + 5)\sqrt{2} = 8\sqrt{2}\)
-
Combine simplified square roots: If the square roots are not like terms, they cannot be combined. For example:
\(3\sqrt{2} + 4\sqrt{3}\) remains \(3\sqrt{2} + 4\sqrt{3}\)
Here is a table summarizing the steps:
| Step | Description | Example |
| 1 | Simplify each square root | \(\sqrt{18} = 3\sqrt{2}\) |
| 2 | Identify like terms | \(3\sqrt{2}\) and \(5\sqrt{2}\) |
| 3 | Add like terms | \(3\sqrt{2} + 5\sqrt{2} = 8\sqrt{2}\) |
| 4 | Combine simplified square roots | \(3\sqrt{2} + 4\sqrt{3} = 3\sqrt{2} + 4\sqrt{3}\) |
By following these steps, you can efficiently add square roots and simplify your expressions.
Identifying Like Terms in Square Roots
Identifying like terms in square roots is essential for simplifying and adding them. Like terms in square roots share the same radicand, which is the number inside the square root. Here’s how you can identify and work with like terms:
-
Understand the Radicand: The radicand is the number under the square root symbol. For example, in \(\sqrt{7}\), the radicand is 7. In \(3\sqrt{5}\), the radicand is 5.
-
Identify Like Radicands: For terms to be considered like terms, their radicands must be identical. For instance, \(2\sqrt{3}\) and \(4\sqrt{3}\) are like terms because both have the radicand 3. However, \(2\sqrt{3}\) and \(3\sqrt{5}\) are not like terms.
-
Check the Coefficients: The coefficients are the numbers multiplied by the square root. While the coefficients can be different, the radicand must be the same for the terms to be like terms. For example, in \(2\sqrt{7}\) and \(5\sqrt{7}\), the coefficients are 2 and 5, respectively, but they are still like terms due to having the same radicand.
Here is a table to illustrate like and unlike terms:
| Expression | Radicand | Like Terms |
| \(2\sqrt{5}\) | 5 | Yes |
| \(7\sqrt{5}\) | 5 | Yes |
| \(3\sqrt{6}\) | 6 | No |
| \(4\sqrt{7}\) | 7 | No |
By focusing on the radicand, you can easily determine if square root terms are like terms, enabling you to add them correctly.
Steps to Simplify Square Roots
Simplifying square roots involves breaking down the number under the radical sign into its prime factors and then simplifying. Here are the detailed steps to simplify square roots:
-
Find the Prime Factorization: Determine the prime factors of the number under the square root. For example, for 72, the prime factorization is \(72 = 2^3 \times 3^2\).
-
Pair the Factors: Group the prime factors into pairs. For instance, \(72 = 2 \times 2 \times 2 \times 3 \times 3\) can be paired as \((2 \times 2) \times 2 \times (3 \times 3)\).
-
Simplify Each Pair: Take one factor from each pair outside the square root. For example, \(\sqrt{72} = \sqrt{(2 \times 2) \times 2 \times (3 \times 3)} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2}\).
-
Combine the Simplified Terms: Multiply the factors taken outside the square root to get the simplified form. In our example, the simplified form of \(\sqrt{72}\) is \(6\sqrt{2}\).
Here is a table to illustrate the steps with different examples:
| Original Expression | Prime Factorization | Simplified Form |
| \(\sqrt{50}\) | \(50 = 2 \times 5^2\) | \(\sqrt{50} = 5\sqrt{2}\) |
| \(\sqrt{18}\) | \(18 = 2 \times 3^2\) | \(\sqrt{18} = 3\sqrt{2}\) |
| \(\sqrt{200}\) | \(200 = 2^3 \times 5^2\) | \(\sqrt{200} = 10\sqrt{2}\) |
| \(\sqrt{45}\) | \(45 = 3^2 \times 5\) | \(\sqrt{45} = 3\sqrt{5}\) |
By following these steps, you can simplify square roots and make them easier to work with in mathematical expressions.

Adding Like Square Roots
Adding like square roots involves combining the coefficients of the square roots that have the same radicand. Here are the detailed steps to add like square roots:
-
Identify the Like Terms: Ensure the square roots have the same radicand. For example, \(3\sqrt{5}\) and \(4\sqrt{5}\) are like terms because they both contain \(\sqrt{5}\).
-
Add the Coefficients: Add the coefficients of the like terms while keeping the common radicand. For example:
\(3\sqrt{5} + 4\sqrt{5} = (3 + 4)\sqrt{5} = 7\sqrt{5}\)
-
Simplify if Necessary: Ensure that the resulting expression is simplified. However, since you are only combining coefficients, further simplification is usually not needed for this step.
Here is a table to illustrate the process with different examples:
| Expression 1 | Expression 2 | Combined Expression |
| \(2\sqrt{3}\) | \(5\sqrt{3}\) | \(2\sqrt{3} + 5\sqrt{3} = 7\sqrt{3}\) |
| \(6\sqrt{2}\) | \(3\sqrt{2}\) | \(6\sqrt{2} + 3\sqrt{2} = 9\sqrt{2}\) |
| \(4\sqrt{7}\) | \(2\sqrt{7}\) | \(4\sqrt{7} + 2\sqrt{7} = 6\sqrt{7}\) |
| \(8\sqrt{11}\) | \(1\sqrt{11}\) | \(8\sqrt{11} + 1\sqrt{11} = 9\sqrt{11}\) |
By following these steps, you can easily add like square roots and simplify your expressions. Remember that the key is ensuring the square roots have the same radicand before combining their coefficients.
Combining Unlike Square Roots
Combining unlike square roots involves simplifying each square root individually but does not allow for direct addition unless the square roots can be simplified to like terms. Here are the steps to handle unlike square roots:
-
Simplify Each Square Root: Begin by simplifying each square root as much as possible. For example, simplify \(\sqrt{18}\) and \(\sqrt{8}\) separately:
- \(\sqrt{18} = \sqrt{9 \times 2} = 3\sqrt{2}\)
- \(\sqrt{8} = \sqrt{4 \times 2} = 2\sqrt{2}\)
-
Check for Like Terms: After simplifying, check if the terms can now be combined. For example:
\(3\sqrt{2}\) and \(2\sqrt{2}\) are like terms, so they can be combined as \(3\sqrt{2} + 2\sqrt{2} = 5\sqrt{2}\).
-
Combine Simplified Terms: If the simplified terms are like terms, combine their coefficients. If they are not like terms, they remain separate. For example:
- \(\sqrt{3} + \sqrt{5}\) cannot be combined and remains as \(\sqrt{3} + \sqrt{5}\).
- \(2\sqrt{3} + 3\sqrt{3} = 5\sqrt{3}\).
Here is a table to illustrate the process with different examples:
| Expression 1 | Expression 2 | Simplified Form |
| \(\sqrt{12}\) | \(\sqrt{27}\) | \(\sqrt{12} = 2\sqrt{3}\), \(\sqrt{27} = 3\sqrt{3}\) => \(2\sqrt{3} + 3\sqrt{3} = 5\sqrt{3}\) |
| \(\sqrt{20}\) | \(\sqrt{45}\) | \(\sqrt{20} = 2\sqrt{5}\), \(\sqrt{45} = 3\sqrt{5}\) => \(2\sqrt{5} + 3\sqrt{5} = 5\sqrt{5}\) |
| \(\sqrt{7}\) | \(\sqrt{11}\) | Cannot be combined, remains \(\sqrt{7} + \sqrt{11}\) |
| \(\sqrt{32}\) | \(\sqrt{18}\) | \(\sqrt{32} = 4\sqrt{2}\), \(\sqrt{18} = 3\sqrt{2}\) => \(4\sqrt{2} + 3\sqrt{2} = 7\sqrt{2}\) |
By following these steps, you can simplify and combine square roots where possible, and clearly identify when they must remain as separate terms.
Examples of Adding Square Roots
Adding square roots involves combining like terms and simplifying the expressions. Here are some detailed examples to illustrate the process step by step:
-
Example 1: Adding like square roots
- Expression: \(2\sqrt{3} + 3\sqrt{3}\)
- Step 1: Identify the like terms. Both terms have \(\sqrt{3}\) as the radicand.
- Step 2: Add the coefficients: \(2 + 3 = 5\).
- Result: \(5\sqrt{3}\).
-
Example 2: Simplifying before adding
- Expression: \(\sqrt{8} + \sqrt{18}\)
- Step 1: Simplify each square root.
- \(\sqrt{8} = \sqrt{4 \times 2} = 2\sqrt{2}\)
- \(\sqrt{18} = \sqrt{9 \times 2} = 3\sqrt{2}\)
- Step 2: Identify the like terms. Both terms have \(\sqrt{2}\) as the radicand.
- Step 3: Add the coefficients: \(2 + 3 = 5\).
- Result: \(5\sqrt{2}\).
-
Example 3: Adding unlike square roots
- Expression: \(\sqrt{5} + \sqrt{7}\)
- Step 1: Simplify each square root if possible (both are already simplified).
- Step 2: Identify the terms. They have different radicands (\(\sqrt{5}\) and \(\sqrt{7}\)), so they cannot be combined.
- Result: The expression remains \(\sqrt{5} + \sqrt{7}\).
-
Example 4: Combining like and unlike square roots
- Expression: \(3\sqrt{2} + \sqrt{50}\)
- Step 1: Simplify \(\sqrt{50}\).
- \(\sqrt{50} = \sqrt{25 \times 2} = 5\sqrt{2}\)
- Step 2: Identify the like terms. Both terms now have \(\sqrt{2}\) as the radicand.
- Step 3: Add the coefficients: \(3 + 5 = 8\).
- Result: \(8\sqrt{2}\).
By following these examples, you can see how to handle different scenarios when adding square roots, whether they are like terms or need to be simplified first.
Common Mistakes and How to Avoid Them
When adding square roots, students often make common mistakes that can lead to incorrect results. Here are some typical errors and how to avoid them:
-
Mistake 1: Adding unlike square roots directly
- Error: Assuming \(\sqrt{3} + \sqrt{5} = \sqrt{8}\)
- Explanation: Unlike square roots cannot be combined unless they are simplified to like terms.
- Solution: Keep unlike square roots separate: \(\sqrt{3} + \sqrt{5}\) remains \(\sqrt{3} + \sqrt{5}\).
-
Mistake 2: Incorrectly simplifying square roots
- Error: Misinterpreting the simplification process, e.g., \(\sqrt{12} = 6\sqrt{2}\).
- Explanation: Correct simplification involves breaking down into prime factors: \(\sqrt{12} = \sqrt{4 \times 3} = 2\sqrt{3}\).
- Solution: Always simplify by identifying prime factors first.
-
Mistake 3: Forgetting to combine like terms
- Error: Leaving like terms uncombined, e.g., \(2\sqrt{3} + 3\sqrt{3} = 2\sqrt{3} + 3\sqrt{3}\).
- Explanation: Like terms should be combined by adding their coefficients.
- Solution: Combine like terms: \(2\sqrt{3} + 3\sqrt{3} = 5\sqrt{3}\).
-
Mistake 4: Incorrectly adding coefficients and radicands
- Error: Adding both coefficients and radicands, e.g., \(2\sqrt{3} + 3\sqrt{3} = 5\sqrt{6}\).
- Explanation: Only the coefficients are added, not the radicands.
- Solution: Keep the radicand the same, and only add coefficients: \(2\sqrt{3} + 3\sqrt{3} = 5\sqrt{3}\).
-
Mistake 5: Neglecting to fully simplify before adding
- Error: Adding terms without first simplifying, e.g., \(\sqrt{18} + \sqrt{8} = \sqrt{18} + \sqrt{8}\).
- Explanation: Simplify each term before adding: \(\sqrt{18} = 3\sqrt{2}\) and \(\sqrt{8} = 2\sqrt{2}\).
- Solution: Simplify and then combine like terms: \(3\sqrt{2} + 2\sqrt{2} = 5\sqrt{2}\).
By being aware of these common mistakes and following the proper steps, you can correctly add square roots and avoid errors in your calculations.
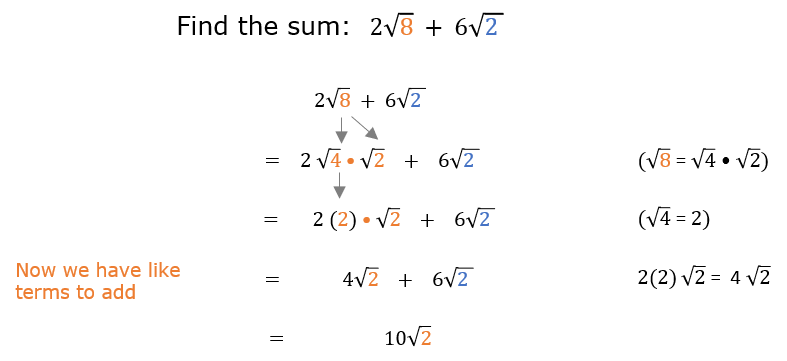
Practice Problems and Solutions
Practicing the addition of square roots can help solidify your understanding. Below are some practice problems followed by detailed solutions.
-
Problem 1: Simplify and add \( \sqrt{12} + \sqrt{27} \)
Solution:
- Simplify each square root:
- \( \sqrt{12} = \sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3} = 2\sqrt{3} \)
- \( \sqrt{27} = \sqrt{9 \times 3} = \sqrt{9} \times \sqrt{3} = 3\sqrt{3} \)
- Add the simplified square roots:
- \( 2\sqrt{3} + 3\sqrt{3} = (2 + 3)\sqrt{3} = 5\sqrt{3} \)
- Final answer: \( 5\sqrt{3} \)
- Simplify each square root:
-
Problem 2: Simplify and add \( 2\sqrt{18} + \sqrt{8} \)
Solution:
- Simplify each square root:
- \( 2\sqrt{18} = 2 \times \sqrt{9 \times 2} = 2 \times 3\sqrt{2} = 6\sqrt{2} \)
- \( \sqrt{8} = \sqrt{4 \times 2} = \sqrt{4} \times \sqrt{2} = 2\sqrt{2} \)
- Add the simplified square roots:
- \( 6\sqrt{2} + 2\sqrt{2} = (6 + 2)\sqrt{2} = 8\sqrt{2} \)
- Final answer: \( 8\sqrt{2} \)
- Simplify each square root:
-
Problem 3: Simplify and add \( \sqrt{50} + 3\sqrt{2} \)
Solution:
- Simplify each square root:
- \( \sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2} \)
- Since \( \sqrt{50} \) is already simplified and \( 3\sqrt{2} \) is in its simplest form, we add the square roots:
- \( 5\sqrt{2} + 3\sqrt{2} = (5 + 3)\sqrt{2} = 8\sqrt{2} \)
- Final answer: \( 8\sqrt{2} \)
- Simplify each square root:
-
Problem 4: Simplify and add \( \sqrt{20} + 2\sqrt{5} \)
Solution:
- Simplify each square root:
- \( \sqrt{20} = \sqrt{4 \times 5} = \sqrt{4} \times \sqrt{5} = 2\sqrt{5} \)
- Since \( \sqrt{20} \) simplifies to \( 2\sqrt{5} \), we add the square roots:
- \( 2\sqrt{5} + 2\sqrt{5} = (2 + 2)\sqrt{5} = 4\sqrt{5} \)
- Final answer: \( 4\sqrt{5} \)
- Simplify each square root:
-
Problem 5: Simplify and add \( \sqrt{18} + \sqrt{50} \)
Solution:
- Simplify each square root:
- \( \sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} = 3\sqrt{2} \)
- \( \sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2} \)
- Add the simplified square roots:
- \( 3\sqrt{2} + 5\sqrt{2} = (3 + 5)\sqrt{2} = 8\sqrt{2} \)
- Final answer: \( 8\sqrt{2} \)
- Simplify each square root:
Advanced Techniques in Adding Square Roots
When dealing with square roots, sometimes you encounter expressions that require advanced techniques to simplify and add them together. Here, we will discuss various methods to handle such cases effectively.
1. Rationalizing Denominators
Sometimes, square root expressions appear in the denominators of fractions. Rationalizing the denominator can make adding square roots easier. Here is how to do it:
- Multiply both the numerator and the denominator by the conjugate of the denominator.
- Simplify the resulting expression.
Example:
Consider \( \frac{1}{\sqrt{2}} + \frac{1}{\sqrt{3}} \).
Step 1: Rationalize the denominators:
\( \frac{1}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2} \) and \( \frac{1}{\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}} = \frac{\sqrt{3}}{3} \).
Step 2: Find a common denominator and add:
\( \frac{\sqrt{2}}{2} + \frac{\sqrt{3}}{3} = \frac{3\sqrt{2} + 2\sqrt{3}}{6} \).
2. Using Algebraic Identities
Certain algebraic identities can help in simplifying and adding square roots. Two useful identities are:
- \( (a+b)^2 = a^2 + 2ab + b^2 \)
- \( (a-b)^2 = a^2 - 2ab + b^2 \)
These identities can be used to combine and simplify square roots before adding them.
Example:
Simplify and add \( \sqrt{a+b} + \sqrt{a-b} \).
Step 1: Assume \( x = \sqrt{a+b} \) and \( y = \sqrt{a-b} \).
Step 2: Use the identities to find \( x^2 \) and \( y^2 \).
\( x^2 = a + b \) and \( y^2 = a - b \).
Step 3: Add the equations:
\( x^2 + y^2 = (a+b) + (a-b) = 2a \).
Thus, \( \sqrt{a+b} + \sqrt{a-b} = \sqrt{2a} \).
3. Decomposition and Grouping
Decomposing square roots and grouping like terms can often simplify the addition process.
Example:
Add \( \sqrt{50} + \sqrt{18} \).
Step 1: Decompose the square roots:
\( \sqrt{50} = \sqrt{25 \cdot 2} = 5\sqrt{2} \)
\( \sqrt{18} = \sqrt{9 \cdot 2} = 3\sqrt{2} \)
Step 2: Group like terms and add:
\( 5\sqrt{2} + 3\sqrt{2} = (5+3)\sqrt{2} = 8\sqrt{2} \).
4. Using the Properties of Radicals
Understanding the properties of radicals can greatly assist in the simplification and addition of square roots:
- \( \sqrt{a} \cdot \sqrt{b} = \sqrt{a \cdot b} \)
- \( \sqrt{a} / \sqrt{b} = \sqrt{a / b} \)
- \( (\sqrt{a})^2 = a \)
Example:
Add \( \sqrt{8} + \sqrt{32} \).
Step 1: Simplify the square roots using the properties of radicals:
\( \sqrt{8} = \sqrt{4 \cdot 2} = 2\sqrt{2} \)
\( \sqrt{32} = \sqrt{16 \cdot 2} = 4\sqrt{2} \)
Step 2: Group like terms and add:
\( 2\sqrt{2} + 4\sqrt{2} = (2+4)\sqrt{2} = 6\sqrt{2} \).
Practice Problems
Try the following problems to apply these advanced techniques:
- Add \( \sqrt{45} + \sqrt{20} \)
- Simplify and add \( \frac{2}{\sqrt{3}} + \frac{3}{\sqrt{2}} \)
- Combine \( \sqrt{12} + \sqrt{27} \)
Solutions:
- \( \sqrt{45} + \sqrt{20} = 3\sqrt{5} + 2\sqrt{5} = 5\sqrt{5} \)
- \( \frac{2}{\sqrt{3}} + \frac{3}{\sqrt{2}} = \frac{2\sqrt{3}}{3} + \frac{3\sqrt{2}}{2} = \frac{4\sqrt{6}}{6} + \frac{9\sqrt{6}}{6} = \frac{13\sqrt{6}}{6} \)
- \( \sqrt{12} + \sqrt{27} = 2\sqrt{3} + 3\sqrt{3} = 5\sqrt{3} \)
Applications of Adding Square Roots
Adding square roots is not just a theoretical exercise; it has numerous practical applications across various fields. Understanding how to manipulate and combine square roots can be incredibly useful in real-world scenarios. Below are some of the key applications:
1. Engineering
In engineering, particularly in the analysis of electrical circuits, the concept of impedance is crucial. Impedance, which is a measure of opposition to the flow of an alternating current, often involves the addition of square roots. For instance, when calculating the total impedance in a series or parallel circuit, engineers may need to add the square roots of individual impedances to find the overall impedance.
2. Physics
In physics, the addition of square roots is commonly seen in wave interference phenomena. When two or more waves overlap, the resulting amplitude can be determined by adding the square roots of the individual amplitudes. This is particularly important in understanding constructive and destructive interference patterns in sound and light waves.
3. Statistics
In statistics, standard deviations and variances are often represented as square roots. When combining data sets, such as finding the combined standard deviation of two independent samples, the process involves adding the square roots of the individual variances.
4. Geometry and Trigonometry
In geometry and trigonometry, adding square roots is frequently used to find distances. For example, the distance formula, which is derived from the Pythagorean theorem, requires adding the square roots of the squared differences in coordinates. This application is essential in fields like computer graphics, navigation, and robotics.
5. Medicine and Pharmacology
In medical dosages and pharmacology, the addition of square roots can be used to calculate the combined effects of different drugs. For instance, when determining the combined efficacy or toxicity of two drugs, researchers may use the square roots of their individual effects to find the overall impact.
6. Economics
Economists use square roots in various models, particularly in risk assessment and portfolio management. The calculation of the combined risk of different investments often involves the addition of the square roots of individual risks, helping to determine the overall risk and return of an investment portfolio.
7. Computer Science
In computer science, algorithms that involve optimization and machine learning may require adding square roots. For example, the Euclidean distance metric, used in clustering algorithms like k-means, involves adding the square roots of squared differences between data points.
Example Application: Electrical Engineering
Consider an example in electrical engineering where we need to find the equivalent impedance (Z) in a series circuit with two components having impedances Z1 and Z2. If Z1 = √3 and Z2 = √5, the total impedance is:
This concept extends to more complex calculations involving series and parallel circuits.
Conclusion
Understanding how to add square roots is essential for solving complex problems in various domains. By mastering this skill, one can tackle challenges in engineering, physics, statistics, and beyond, making it a valuable tool in both academic and professional settings.
Conclusion
Adding square roots is a fundamental skill in algebra that becomes increasingly useful in various mathematical and real-world applications. Throughout this guide, we have explored the basic principles, common techniques, and advanced strategies for combining square roots. Here, we summarize the key takeaways:
- Understanding Square Roots: Recognizing that the square root of a number is a value that, when multiplied by itself, gives the original number. This foundational knowledge is crucial for performing operations with square roots.
- Like Terms: Only square roots with the same radicand (the number under the square root) can be directly added or subtracted. Simplifying square roots before combining them ensures that like terms are accurately identified.
- Simplification: Often, square roots need to be simplified before they can be combined. This involves factoring the radicand into its prime components and simplifying wherever possible.
- Combining Like Terms: Once simplified, like terms can be added or subtracted by combining their coefficients, much like in polynomial operations.
- Applications: The ability to add and simplify square roots is not only essential in algebra but also in fields such as engineering, physics, and computer science where complex calculations often involve radicals.
In practice, mastering the addition of square roots enhances problem-solving skills and mathematical understanding. By following the steps outlined in this guide and practicing with various problems, one can develop a strong proficiency in handling square roots. Remember, the key is consistent practice and application of the rules discussed.
As you continue to work with square roots, always check for opportunities to simplify and combine like terms. This will not only make your calculations easier but also deepen your understanding of the underlying mathematical concepts.
We hope this comprehensive guide has provided you with the knowledge and tools needed to confidently add square roots. Keep practicing, and you'll find that this skill becomes an integral part of your mathematical toolkit.
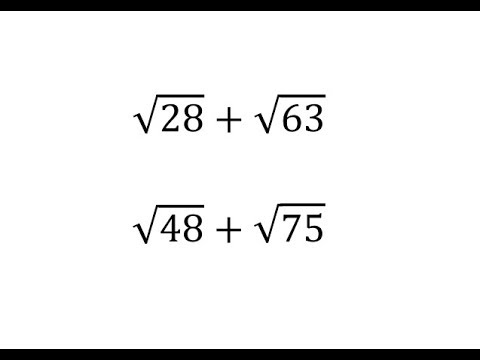
Hướng dẫn cách thêm và trừ biểu thức căn bậc hai và căn bậc ba một cách chi tiết và dễ hiểu. Phù hợp cho người học ở mọi cấp độ.
Thêm và Trừ Biểu Thức Căn Bậc Hai và Căn Bậc Ba
READ MORE:
Hướng dẫn chi tiết về cách thêm và trừ căn bậc hai, phù hợp cho người học muốn hiểu rõ hơn về các biểu thức căn bậc hai.
Cách Thêm và Trừ Căn Bậc Hai