Topic square root simplified: Understanding how to simplify square roots is a fundamental skill in algebra. This article will guide you through the process of simplifying square roots, providing step-by-step examples and helpful tips to make this concept easy to grasp. Whether you're a student or just looking to brush up on your math skills, this guide is for you.
Table of Content
- Understanding Square Root Simplification
- Introduction to Square Roots
- Basic Concepts of Square Roots
- Prime Factorization Method
- Common Mistakes in Simplifying Square Roots
- Examples of Simplified Square Roots
- Using Square Roots in Equations
- Square Roots in Geometry and Algebra
- Advanced Techniques in Square Root Simplification
- Practice Problems for Simplifying Square Roots
- Benefits of Mastering Square Root Simplification
- Resources for Further Learning
- Conclusion
- YOUTUBE:
Understanding Square Root Simplification
The process of simplifying square roots is essential in mathematics, making complex expressions easier to work with. This guide explains the steps to simplify square roots, using MathJax for clear mathematical notation.
Steps to Simplify Square Roots
- Identify the prime factors of the number under the square root.
- Pair the prime factors in groups of two.
- Move each pair of prime factors outside the square root.
- Multiply the numbers outside the square root.
- Leave any unpaired prime factors inside the square root.
Example: Simplifying the Square Root of 75
Let's simplify \( \sqrt{75} \).
- Find the prime factors of 75: \( 75 = 3 \times 5 \times 5 \).
- Identify pairs of prime factors: \( 75 = 3 \times 5^2 \).
- Move the pair of 5s outside the square root: \( \sqrt{75} = 5\sqrt{3} \).
Thus, the simplified form of \( \sqrt{75} \) is \( 5\sqrt{3} \).
Additional Examples
Here are more examples to illustrate the simplification process:
- \( \sqrt{50} = \sqrt{2 \times 5^2} = 5\sqrt{2} \)
- \( \sqrt{98} = \sqrt{2 \times 7^2} = 7\sqrt{2} \)
- \( \sqrt{45} = \sqrt{3^2 \times 5} = 3\sqrt{5} \)
Benefits of Simplifying Square Roots
- Makes calculations easier and more manageable.
- Helps in solving equations involving square roots.
- Simplifies expressions in geometry and algebra.
Practice Problems
Try simplifying these square roots on your own:
- \( \sqrt{32} \)
- \( \sqrt{72} \)
- \( \sqrt{128} \)
Practice regularly to master the skill of simplifying square roots.

READ MORE:
Introduction to Square Roots
The concept of square roots is fundamental in mathematics, representing a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3, since 3 * 3 = 9. This section will guide you through the basics of square roots and their simplification.
To simplify a square root, the goal is to make the number inside the square root as small as possible while ensuring it remains a whole number. The process involves breaking down the number into its prime factors and applying the rule:
When \( a \) and \( b \) are not negative:
\[ \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \]
Here is a step-by-step example to illustrate:
- Example: Simplify \(\sqrt{12}\)
- Identify the factors of 12: 12 = 4 × 3
- Apply the rule: \(\sqrt{12} = \sqrt{4 \cdot 3} = \sqrt{4} \cdot \sqrt{3}\)
- Since the square root of 4 is 2: \(\sqrt{4} \cdot \sqrt{3} = 2\sqrt{3}\)
- Therefore, \(\sqrt{12}\) simplifies to \(2\sqrt{3}\)
Other examples include:
- \(\sqrt{45} = 3\sqrt{5}\)
- \(\sqrt{8} = 2\sqrt{2}\)
- \(\sqrt{18} = 3\sqrt{2}\)
Understanding these basic steps makes it easier to handle more complex square root problems and simplifies calculations in various mathematical contexts.
Basic Concepts of Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. Square roots are fundamental in mathematics, often appearing in algebra, geometry, and various calculations. Let's explore the basic concepts of square roots step by step:
- Definition:
The square root of a number \( x \) is a number \( y \) such that \( y^2 = x \). It is denoted as \( \sqrt{x} \). For example, \( \sqrt{25} = 5 \) because \( 5^2 = 25 \).
- Properties:
\( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \): This property allows us to break down the square root of a product into the product of the square roots.
\( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \): This property helps in simplifying square roots of fractions.
For any positive number \( a \), \( \left(\sqrt{a}\right)^2 = a \).
- Simplifying Square Roots:
To simplify a square root, factorize the number under the square root into its prime factors and pair the common factors.
Example: Simplify \( \sqrt{12} \)
- Factorize 12: \( 12 = 4 \times 3 \)
- Use the property: \( \sqrt{12} = \sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3} \)
- Simplify: \( \sqrt{4} = 2 \), so \( \sqrt{12} = 2\sqrt{3} \)
Example: Simplify \( \sqrt{45} \)
- Factorize 45: \( 45 = 9 \times 5 \)
- Use the property: \( \sqrt{45} = \sqrt{9 \times 5} = \sqrt{9} \times \sqrt{5} \)
- Simplify: \( \sqrt{9} = 3 \), so \( \sqrt{45} = 3\sqrt{5} \)
- Applications:
Square roots are used in various fields such as algebra for solving quadratic equations, in geometry for calculating distances and lengths using the Pythagorean theorem, and in real-world scenarios like physics and engineering.
Prime Factorization Method
The prime factorization method is a systematic approach to simplify square roots by breaking down the number into its prime factors. Here is a step-by-step guide to using this method:
- Decompose the Number: Start by breaking down the number into its prime factors. For example, let's simplify the square root of 48. The prime factorization of 48 is \(2 \times 2 \times 2 \times 2 \times 3\).
- Group the Prime Factors: Arrange the prime factors in pairs. For 48, we can group it as \(\sqrt{(2 \times 2) \times (2 \times 2) \times 3}\).
- Simplify the Expression: Since 48 contains perfect square factors (such as \(2 \times 2 = 4\)), we can simplify the expression to obtain the square root in radical form. This results in \(4\sqrt{3}\).
In summary, the square root of 48 simplifies to \(4\sqrt{3}\) using the prime factorization method. This method is particularly useful for simplifying square roots of larger numbers, making the process clear and manageable.
Common Mistakes in Simplifying Square Roots
Understanding square roots is essential, but it's easy to make mistakes when simplifying them. Here are some common pitfalls to avoid:
- Forgetting Perfect Squares: Before starting the simplification process, always check if the number is a perfect square. For instance, \( \sqrt{25} \) should be immediately recognized as 5.
- Rushing the Process: Simplifying square roots requires careful step-by-step calculations. Hurrying can lead to errors.
- Ignoring Prime Factorization: Not using prime factorization to break down the number under the square root can lead to incorrect simplifications. For example, \( \sqrt{72} \) can be simplified by recognizing \( 72 = 2^3 \times 3^2 \).
- Mistakes in Multiplication: Errors often occur when multiplying or combining terms inside and outside the square root. Always double-check your multiplication.
To avoid these mistakes, follow these detailed steps:
- Identify if the number under the square root is a perfect square.
- If not, use prime factorization to break down the number into its prime factors.
- Group the prime factors in pairs.
- Move each pair of prime factors outside the square root.
- Simplify the expression by multiplying the numbers outside the square root and those remaining inside.
By being aware of these common mistakes and following these steps, you can master the art of simplifying square roots with confidence and accuracy.
Examples of Simplified Square Roots
Here are some examples to help you understand how to simplify square roots:
-
Simplify \(\sqrt{50}\):
\[
\sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2}
\] -
Simplify \(\sqrt{72}\):
\[
\sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2}
\] -
Simplify \(\sqrt{128}\):
\[
\sqrt{128} = \sqrt{64 \times 2} = \sqrt{64} \times \sqrt{2} = 8\sqrt{2}
\] -
Simplify \(\sqrt{18}\):
\[
\sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} = 3\sqrt{2}
\] -
Simplify \(\sqrt{200}\):
\[
\sqrt{200} = \sqrt{100 \times 2} = \sqrt{100} \times \sqrt{2} = 10\sqrt{2}
\]
These examples illustrate the process of breaking down the number inside the square root into its prime factors and then simplifying.
Using Square Roots in Equations
Square roots are often used in solving various types of equations, particularly quadratic equations. Here are the steps and methods to use square roots effectively in equations:
1. Solving Quadratic Equations Using the Square Root Method
Quadratic equations of the form \( ax^2 + bx + c = 0 \) can sometimes be solved using the square root method. This method is particularly useful when the equation can be simplified to the form \( x^2 = k \).
- Isolate the Quadratic Term: Move all terms to one side of the equation so that you have \( x^2 \) by itself. For example, \( x^2 = k \).
- Take the Square Root of Both Sides: Apply the square root to both sides of the equation. Remember that taking the square root of \( x^2 \) will yield both positive and negative roots. This can be expressed as \( x = \pm \sqrt{k} \).
- Simplify the Radical: If possible, simplify the square root. For example, \( \sqrt{50} = \sqrt{25 \cdot 2} = 5\sqrt{2} \).
- Write the Final Solution: Include both the positive and negative solutions. For example, \( x = \pm 5\sqrt{2} \).
2. Examples
Let's go through some specific examples to illustrate the process:
- Example 1: Solve \( x^2 = 9 \)
- Isolate the quadratic term: \( x^2 = 9 \)
- Take the square root of both sides: \( x = \pm \sqrt{9} \)
- Simplify the radical: \( x = \pm 3 \)
- Solution: \( x = 3 \) or \( x = -3 \)
- Example 2: Solve \( x^2 - 50 = 0 \)
- Isolate the quadratic term: \( x^2 = 50 \)
- Take the square root of both sides: \( x = \pm \sqrt{50} \)
- Simplify the radical: \( x = \pm 5\sqrt{2} \)
- Solution: \( x = 5\sqrt{2} \) or \( x = -5\sqrt{2} \)
- Example 3: Solve \( 3x^2 = 108 \)
- Isolate the quadratic term: \( x^2 = \frac{108}{3} = 36 \)
- Take the square root of both sides: \( x = \pm \sqrt{36} \)
- Simplify the radical: \( x = \pm 6 \)
- Solution: \( x = 6 \) or \( x = -6 \)
3. Applying Square Roots in Other Types of Equations
Square roots are not limited to quadratic equations. They are also used in other types of mathematical problems such as geometry and algebra:
- Geometry: Calculating the length of the hypotenuse in a right triangle using the Pythagorean theorem: \( c = \sqrt{a^2 + b^2} \).
- Algebra: Simplifying expressions that involve square roots, such as \( \sqrt{x^2 + y^2} \).
By mastering the use of square roots in equations, you can solve a wide range of mathematical problems efficiently. Practice these steps with different equations to become more confident in your skills.
Square Roots in Geometry and Algebra
Square roots play a significant role in both geometry and algebra. They are fundamental in solving various mathematical problems, from determining the lengths of sides in geometric shapes to simplifying algebraic expressions.
Square Roots in Geometry
In geometry, square roots are commonly used to find the lengths of sides in right-angled triangles through the Pythagorean theorem. The theorem states that for a right-angled triangle with legs \(a\) and \(b\) and hypotenuse \(c\):
\[ c = \sqrt{a^2 + b^2} \]
For example, if \(a = 3\) and \(b = 4\), then the length of the hypotenuse \(c\) is:
\[ c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]
Square roots are also essential in determining areas and other properties of geometric shapes, such as circles and squares. For instance, the radius \(r\) of a circle with area \(A\) can be found using:
\[ r = \sqrt{\frac{A}{\pi}} \]
Square Roots in Algebra
In algebra, square roots are used to simplify expressions and solve equations. Here are some key points and steps for using square roots in algebraic contexts:
- Solving Quadratic Equations: Quadratic equations of the form \(ax^2 + bx + c = 0\) can be solved using the quadratic formula, where the square root is crucial:
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
- Simplifying Radicals: To simplify expressions involving square roots, factor the radicand (the number under the square root) into its prime factors and then apply the product rule for square roots:
- Example: Simplify \(\sqrt{50}\)
\[ \sqrt{50} = \sqrt{2 \times 5^2} = 5\sqrt{2} \]
- Example: Simplify \(\sqrt{50}\)
- Operations with Radicals: Addition, subtraction, multiplication, and division can be performed on expressions involving square roots, similar to other algebraic terms, provided the radicals have the same index and radicand:
- Example: Adding \(\sqrt{3}\) and \(2\sqrt{3}\):
\[ \sqrt{3} + 2\sqrt{3} = 3\sqrt{3} \]
- Example: Adding \(\sqrt{3}\) and \(2\sqrt{3}\):
- Using the Quotient Property: The square root of a fraction can be simplified by taking the square root of the numerator and the denominator separately:
- Example: Simplify \(\sqrt{\frac{16}{25}}\):
\[ \sqrt{\frac{16}{25}} = \frac{\sqrt{16}}{\sqrt{25}} = \frac{4}{5} \]
- Example: Simplify \(\sqrt{\frac{16}{25}}\):
Understanding and mastering the use of square roots in both geometry and algebra enhances problem-solving skills and provides a solid foundation for more advanced mathematical concepts.
Advanced Techniques in Square Root Simplification
Simplifying square roots can become more manageable and efficient with advanced techniques. These methods are particularly useful for handling complex numbers or larger expressions. Below are some advanced techniques to simplify square roots:
- Rationalizing the Denominator: When a square root appears in the denominator, multiply both the numerator and the denominator by the square root to eliminate it. This simplifies the expression and makes it easier to work with.
For example:
\[
\frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}
\] - Using Conjugates: For expressions involving square roots in the denominator, use the conjugate of the denominator to rationalize. The conjugate reverses the sign between two terms in a binomial. Multiplying the numerator and the denominator by the conjugate simplifies the square root.
For example:
\[
\frac{1}{\sqrt{3} + 1} \times \frac{\sqrt{3} - 1}{\sqrt{3} - 1} = \frac{\sqrt{3} - 1}{2}
\] - Applying the Binomial Theorem: For expressions involving powers of square roots, the binomial theorem can be used to expand and simplify them, especially when dealing with polynomial expressions including square roots.
For example:
\[
(\sqrt{x} + 1)^2 = x + 2\sqrt{x} + 1
\] - Decomposition into Simpler Parts: Complex square roots can sometimes be broken down into simpler parts that are easier to simplify individually, then recombined into a simplified whole.
For example:
\[
\sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2}
\] - Leveraging Algebraic Identities: Use algebraic identities to simplify square roots, especially when they are part of algebraic expressions. Recognizing patterns that fit certain identities, like the difference of squares, can simplify the process.
For example:
\[
\sqrt{a^2 - b^2} = \sqrt{(a+b)(a-b)}
\]
By mastering these advanced techniques, you can enhance your mathematical skills and simplify even the most complex square root expressions effectively.

Practice Problems for Simplifying Square Roots
Practicing the simplification of square roots is essential for mastering this concept. Below are a series of practice problems designed to help you understand and apply various techniques for simplifying square roots.
- Simplify \( \sqrt{50} \)
- Simplify \( \sqrt{72} \)
- Simplify \( \sqrt{18} \)
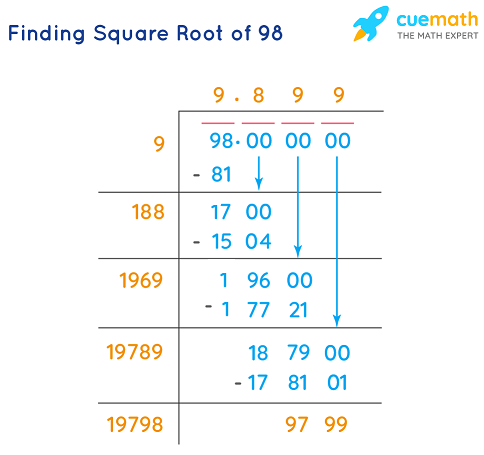
- Simplify \( \sqrt{98} \)
- Simplify \( \sqrt{45} \)
Here are the steps to simplify these square roots:
- Identify the prime factors of the number inside the square root.
- Pair the prime factors in groups of two.
- For each pair of factors, move one factor out of the square root.
- Multiply the factors outside the square root to get the simplified form.
Let's go through the first example step by step:
Simplify \( \sqrt{50} \):
- Find the prime factors of 50: \( 50 = 2 \times 5 \times 5 \)
- Pair the factors: \( (5 \times 5) \times 2 \)
- Move the paired factors out of the square root: \( 5 \sqrt{2} \)
Therefore, \( \sqrt{50} = 5 \sqrt{2} \).
Continue practicing with the other examples provided. Below are additional problems to further enhance your skills:
| Problem | Simplified Form |
|---|---|
| \( \sqrt{72} \) | \( 6 \sqrt{2} \) |
| \( \sqrt{18} \) | \( 3 \sqrt{2} \) |
| \( \sqrt{98} \) | \( 7 \sqrt{2} \) |
| \( \sqrt{45} \) | \( 3 \sqrt{5} \) |
For a more in-depth understanding, try to solve these problems step by step on your own before looking at the simplified forms. Consistent practice will help you master the technique of simplifying square roots.
Here are some additional problems to challenge your understanding:
- Simplify \( \sqrt{128} \)
- Simplify \( \sqrt{200} \)
- Simplify \( \sqrt{242} \)
- Simplify \( \sqrt{288} \)
- Simplify \( \sqrt{392} \)
Benefits of Mastering Square Root Simplification
Mastering the simplification of square roots offers numerous benefits across various fields of mathematics and beyond. Here are some key advantages:
- Enhanced Problem-Solving Skills: Simplifying square roots helps in solving more complex mathematical problems efficiently. It forms the foundation for tackling algebraic expressions, quadratic equations, and higher-level mathematics.
- Improved Mathematical Understanding: Understanding the principles behind square root simplification deepens your comprehension of number properties and relationships, which is essential for advanced math studies.
- Applications in Geometry: Simplifying square roots is crucial in geometry, especially when dealing with Pythagorean Theorem, calculating distances, and solving problems involving right triangles.
- Utilization in Algebra: Algebraic manipulations often require simplified square roots for solving equations, simplifying expressions, and working with radicals in polynomial and rational functions.
- Precision in Calculations: Simplified square roots provide more precise and manageable forms of numbers, making calculations easier and more accurate.
- Preparation for Advanced Mathematics: Mastery of square root simplification prepares students for more advanced topics in calculus, complex numbers, and higher-level algebra.
- Real-World Applications: Many real-world applications, such as physics, engineering, and computer science, involve the use of square roots. Simplifying these roots is essential for efficient problem-solving and analysis.
By mastering square root simplification, you not only enhance your mathematical skills but also equip yourself with tools essential for academic and professional success.
Resources for Further Learning
Mastering the simplification of square roots can be significantly aided by utilizing various resources available online and offline. Here are some valuable resources to deepen your understanding and practice your skills:
- Online Tutorials and Courses:
- - Comprehensive video tutorials and practice problems on simplifying square roots and other radical expressions.
- - A structured course covering various algebra topics, including square roots.
- Mathematics Textbooks:
- Algebra and Trigonometry by Robert Blitzer - A widely used textbook that offers detailed explanations and exercises on square roots and radicals.
- Precalculus by James Stewart, Lothar Redlin, and Saleem Watson - Provides in-depth coverage of algebraic concepts, including square roots, with numerous examples and practice problems.
- Interactive Websites:
- - An interactive platform with explanations, examples, and quizzes on square roots.
- - Offers clear lessons and practice problems focused on simplifying square roots and other radical expressions.
- Worksheets and Practice Problems:
- - Printable worksheets with various levels of difficulty to practice simplifying square roots.
- - Step-by-step guides and practice problems to help you master the simplification of square roots.
- Mobile Apps:
- - An app that allows you to take pictures of math problems and provides step-by-step solutions, including simplifying square roots.
- - A powerful calculator app that offers detailed solutions and explanations for algebraic problems, including square roots.
Using these resources, you can enhance your understanding of square root simplification, practice effectively, and gain confidence in handling more complex algebraic problems involving radicals.
Conclusion
Mastering the simplification of square roots is a valuable skill that enhances mathematical understanding and problem-solving abilities. Throughout this guide, we have explored various methods and techniques to simplify square roots effectively. By breaking down the steps, utilizing prime factorization, and avoiding common mistakes, you can confidently tackle square root problems with ease.
Here are the key takeaways from this comprehensive guide:
- Understanding the Basics: A strong grasp of basic square root concepts sets the foundation for more advanced techniques.
- Prime Factorization: Breaking down numbers into their prime factors is a fundamental method to simplify square roots.
- Common Mistakes: Awareness of common errors ensures accuracy in calculations and prevents misunderstandings.
- Practical Examples: Practicing with a variety of examples solidifies the concepts and demonstrates their real-world applications.
- Application in Equations: Simplified square roots are crucial in solving algebraic and geometric equations efficiently.
- Advanced Techniques: For those looking to deepen their knowledge, exploring advanced techniques opens new avenues of mathematical exploration.
- Continuous Practice: Regular practice with diverse problems strengthens skills and boosts confidence in handling complex square root simplifications.
By mastering these skills, you not only improve your mathematical proficiency but also gain a deeper appreciation for the elegance and utility of square roots in various mathematical contexts. Keep practicing, stay curious, and continue exploring the fascinating world of mathematics.
For further learning and practice, explore additional resources and tools available online, such as interactive calculators and step-by-step guides. These resources can provide additional support and enhance your learning experience.
Thank you for taking the time to delve into the intricacies of square root simplification. Happy learning!

Cách Đơn Giản Hóa Căn Bậc Hai
READ MORE:
Toán Antic - Đơn Giản Hóa Căn Bậc Hai