Topic what is the square root of 40 simplified: Discover how to simplify the square root of 40 effortlessly. This guide breaks down the process into simple steps, making it easy for anyone to grasp. Whether you're a student or just curious, you'll find clear explanations and useful tips to understand and apply the concept of square root simplification in no time.
Table of Content
- Square Root of 40 Simplified
- Introduction to Square Root Simplification
- Understanding Square Roots
- Basics of Prime Factorization
- Simplifying the Square Root of 40
- Mathematical Explanation and Calculation
- Visual Representation of the Simplification
- Importance of Simplifying Square Roots
- Applications of Simplified Square Roots
- Practice Problems
- Common Mistakes and How to Avoid Them
- YOUTUBE: Hướng dẫn chi tiết về cách đơn giản hóa căn bậc hai của 40. Video này sẽ giúp bạn hiểu rõ và dễ dàng thực hiện các bước cần thiết.
Square Root of 40 Simplified
The square root of 40 can be simplified by expressing it in terms of the square root of its prime factors.
Steps to Simplify the Square Root of 40
- Find the prime factorization of 40.
- Express 40 as a product of its prime factors.
- Simplify the square root by pairing the prime factors.
Prime Factorization of 40
The prime factorization of 40 is:
\[ 40 = 2 \times 2 \times 2 \times 5 \]
Expressing 40 as a Product of its Prime Factors
Using the prime factorization, we can write:
\[ 40 = 2^2 \times 10 \]
Simplifying the Square Root
The square root of 40 is:
\[ \sqrt{40} \]
We can simplify this as:
\[ \sqrt{40} = \sqrt{2^2 \times 10} \]
Taking the square root of the perfect square (22):
\[ \sqrt{2^2 \times 10} = 2 \sqrt{10} \]
Final Simplified Form
Therefore, the simplified form of the square root of 40 is:
\[ \sqrt{40} = 2 \sqrt{10} \]
Conclusion
The square root of 40 simplifies to \( 2 \sqrt{10} \). This is the most simplified form of the square root of 40.

READ MORE:
Introduction to Square Root Simplification
Simplifying square roots is an essential skill in mathematics that helps in reducing complex expressions into more manageable forms. The process involves breaking down a number into its prime factors and pairing them to simplify the square root. Here is a detailed step-by-step guide to understanding and simplifying square roots:
Step-by-Step Guide
- Understand Square Roots: The square root of a number is a value that, when multiplied by itself, gives the original number. For example, \(\sqrt{16} = 4\) because \(4 \times 4 = 16\).
- Identify Perfect Squares: Recognize numbers that are perfect squares (e.g., 1, 4, 9, 16, 25, etc.). These numbers have whole numbers as their square roots.
- Prime Factorization: Break down the number under the square root into its prime factors. For example, the prime factorization of 40 is \(2 \times 2 \times 2 \times 5\).
- Group the Factors: Pair the prime factors into groups of two. In our example, \(40 = 2^2 \times 10\), where \(2^2\) forms a pair.
- Simplify the Square Root: Take one factor from each pair out of the square root. For \(40\), this simplifies to \(2 \sqrt{10}\).
By following these steps, you can simplify any square root, making complex calculations easier to manage and understand.
Understanding Square Roots
Square roots are a fundamental concept in mathematics, representing a value that, when multiplied by itself, yields the original number. Here, we will explore the concept of square roots in detail, using examples to illustrate the steps involved in understanding and calculating them.
Definition and Basic Concept
The square root of a number \( x \) is denoted as \( \sqrt{x} \) and is defined as the number \( y \) such that \( y \times y = x \). In other words:
\[ \sqrt{x} = y \text{ if and only if } y^2 = x \]
Perfect Squares
A perfect square is a number that can be expressed as the square of an integer. For example:
- \( 1 = 1^2 \)
- \( 4 = 2^2 \)
- \( 9 = 3^2 \)
- \( 16 = 4^2 \)
- \( 25 = 5^2 \)
These numbers have whole numbers as their square roots, making them straightforward to calculate.
Non-Perfect Squares
For numbers that are not perfect squares, the square root is an irrational number. For example, the square root of 2 (\( \sqrt{2} \)) is approximately 1.414 and cannot be expressed as a precise fraction.
Square Root Calculation
To calculate the square root of a number that is not a perfect square, you can use methods such as prime factorization, approximation, or a calculator. Here’s a detailed step-by-step example using prime factorization:
- Prime Factorization: Break down the number into its prime factors. For example, 40 can be factored into \( 2 \times 2 \times 2 \times 5 \).
- Pair the Factors: Group the prime factors into pairs. For 40, this is \( 2^2 \times 10 \).
- Extract the Pairs: Take one factor from each pair outside the square root. This gives us \( 2 \sqrt{10} \).
Understanding these principles allows you to simplify square roots and work with them more effectively in various mathematical contexts.
Basics of Prime Factorization
Prime factorization is the process of breaking down a composite number into its prime factors, which are prime numbers that multiply together to give the original number. Understanding prime factorization is essential for simplifying square roots and performing various other mathematical operations. Here is a detailed step-by-step guide to prime factorization:
Step-by-Step Guide
- Identify the Number: Start with the composite number you want to factorize. For example, let's use 40.
- Divide by the Smallest Prime: Begin by dividing the number by the smallest prime number, which is 2. Continue dividing by 2 until you can no longer divide evenly. For 40:
- 40 ÷ 2 = 20
- 20 ÷ 2 = 10
- 10 ÷ 2 = 5
- Move to the Next Prime: Once you can no longer divide by 2, move to the next smallest prime number, which is 3. In this case, 3 does not divide 5 evenly, so we move to 5.
- 5 ÷ 5 = 1
- List the Prime Factors: After completing the divisions, list all the prime factors. For 40, the prime factors are:
- 2, 2, 2, 5
Prime Factorization Example
To summarize, the prime factorization of 40 is expressed as:
\[ 40 = 2 \times 2 \times 2 \times 5 \]
Or in exponential form:
\[ 40 = 2^3 \times 5 \]
Understanding prime factorization allows you to break down numbers into their basic building blocks, which can then be used for further simplification and calculation, such as simplifying square roots.
Simplifying the Square Root of 40
The square root of 40 can be simplified by breaking it down into its prime factors and applying the product rule for radicals. Here’s a detailed step-by-step process to simplify √40:
- Prime Factorization: Begin by finding the prime factors of 40. The prime factorization of 40 is:
- 40 = 2 × 2 × 2 × 5
- Group the Prime Factors: Next, group the prime factors in pairs:
- √40 = √(2 × 2 × 2 × 5) = √(2² × 2 × 5)
- Apply the Square Root to the Pairs: For the pair of 2s under the square root, take one 2 out of the radical:
- √(2² × 2 × 5) = 2√(2 × 5)
- Simplify the Expression: Multiply the terms outside and inside the radical:
- 2√(2 × 5) = 2√10
Therefore, the simplified form of the square root of 40 is:
To verify, you can use a calculator to find that 2√10 is approximately 6.3246, which matches the decimal form of √40.
This simplification process helps in various mathematical applications, making calculations easier and more efficient. Understanding how to simplify square roots is a fundamental skill in algebra that applies to more complex problems involving radicals.
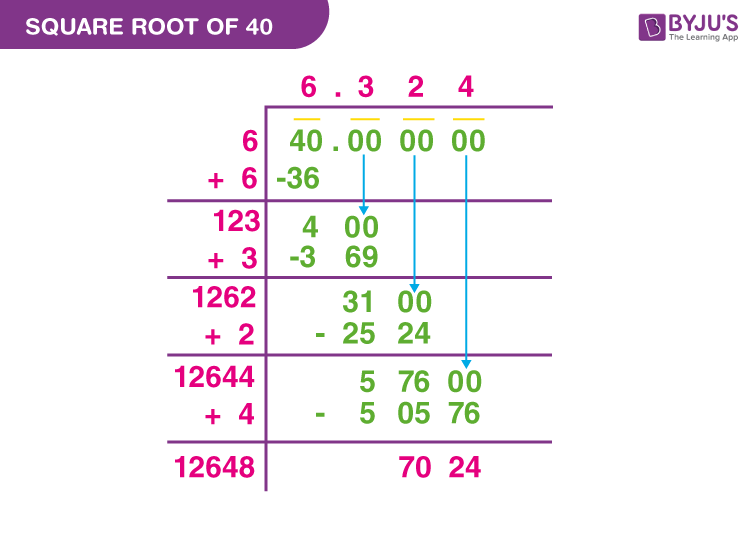
Mathematical Explanation and Calculation
To simplify the square root of 40, we need to follow a series of steps that involve prime factorization and the properties of square roots. Here is a detailed mathematical explanation and calculation:
-
Start with the original expression:
\[\sqrt{40}\]
-
Find the prime factorization of 40:
\[40 = 2 \times 2 \times 2 \times 5\]
-
Group the prime factors into pairs:
\[\sqrt{40} = \sqrt{(2 \times 2) \times 2 \times 5}\]
-
Simplify the pairs inside the square root:
\[\sqrt{(2 \times 2) \times 2 \times 5} = \sqrt{4 \times 10} = \sqrt{4} \times \sqrt{10}\]
-
Calculate the square root of the perfect square:
\[\sqrt{4} = 2\]
-
Combine the results:
\[\sqrt{40} = 2 \sqrt{10}\]
Therefore, the simplified form of the square root of 40 is:
\[2 \sqrt{10}\]
In decimal form, this can be approximated as:
\[2 \sqrt{10} \approx 2 \times 3.162 = 6.324\]
This step-by-step process shows how we simplify \(\sqrt{40}\) to \(2 \sqrt{10}\), providing both the exact form and an approximate decimal value for better understanding.
Visual Representation of the Simplification
Visualizing the simplification of the square root of 40 can help in understanding the process better. Here's a step-by-step visual representation:
- First, recognize that can be simplified using its prime factors.
- The prime factorization of 40 is 2 × 2 × 2 × 5, or .
- Pair the identical factors under the square root:
To visualize this:
- Draw a rectangle to represent the product 2 × 2 × 2 × 5.
- Group a pair of 2s under the square root and simplify to get 2 outside the square root.
- You are left with 2 outside the square root and 10 inside.
- This process shows how simplifies to 2
10 .
Below is a table summarizing the process:
| Step | Expression |
|---|---|
| Original | |
| Prime Factorization | |
| Simplify |
Here’s a visual breakdown:
- Draw a rectangle divided into 40 smaller squares.
- Group them into pairs of 2s wherever possible.
- Highlight the pair that comes out of the square root (2).
- Show the remaining under the square root (10).
This method not only simplifies the square root but also provides a clear visual understanding of the process.
Importance of Simplifying Square Roots
Simplifying square roots is a crucial skill in mathematics that offers several benefits:
- Ease of Calculation: Simplified square roots make it easier to perform arithmetic operations, especially when dealing with more complex expressions.
- Clarity and Precision: Simplified forms are more straightforward and less cluttered, which helps in understanding and solving problems more accurately.
- Standardization: Simplifying square roots is a standard practice in mathematical conventions, ensuring consistency across various calculations and disciplines.
- Application in Higher Mathematics: Simplified square roots are foundational for more advanced topics in algebra, calculus, and beyond, where precise and simplified forms are necessary for proofs and derivations.
Consider the square root of 40:
- We simplify \(\sqrt{40}\) to its simplest radical form to facilitate easier multiplication, addition, or other operations.
- This simplification helps in visualizing and graphing functions, especially in trigonometry and calculus where roots often appear.
- For instance, simplifying \(\sqrt{40}\) to \(2\sqrt{10}\) can be essential in solving quadratic equations or integrals.
Furthermore, understanding the importance of simplification aids in avoiding common mistakes such as misinterpreting or mishandling more complex roots. It ensures that mathematical communication is clear, precise, and universally understood.
Applications of Simplified Square Roots
The simplified form of square roots is essential in various real-world applications. Below are some key applications:
- Geometry and Measurement:
Simplified square roots are used to calculate distances, areas, and volumes in geometric problems. For example, finding the length of the diagonal of a square with a given area.
- Physics and Engineering:
In physics and engineering, simplified square roots are used in formulas that describe wave speeds, electrical circuits, and other phenomena. For example, the formula for the resonant frequency of an LC circuit includes the square root of inductance and capacitance.
- Architecture and Construction:
Architects and builders use simplified square roots to ensure accurate measurements and proportions. For instance, calculating the correct lengths for supports in structures.
- Computer Science and Algorithms:
Algorithms in computer science, such as those for graphics rendering and data analysis, often use simplified square roots to optimize performance and accuracy.
- Astronomy:
Astronomers use simplified square roots in their calculations to determine distances between celestial objects and to analyze the properties of stars and planets.
- Everyday Calculations:
In daily life, simplified square roots help in quick mental calculations, such as determining the dimensions of a square area from its given size or estimating the length of the sides of a rectangular space.
Understanding and using simplified square roots allow for more efficient and accurate problem-solving across various fields, showcasing their importance in both theoretical and practical applications.

Practice Problems
Here are some practice problems to help you master the simplification of square roots, using the methods we've discussed for the square root of 40.
- Simplify the square root of 18.
- Simplify the square root of 50.
- Simplify the square root of 72.
- Simplify the square root of 98.
- Simplify the square root of 128.
Follow the steps below to solve each problem:
- Prime Factorization: Write the number as a product of its prime factors.
- Group Factors: Group the prime factors into pairs.
- Simplify: Pull out one factor from each pair outside the square root.
- Calculate: Multiply the factors outside the square root.
Let's go through the first problem together:
Simplify the square root of 18:
- Prime Factorization of 18: \( 18 = 2 \times 3 \times 3 \)
- Group Factors: \( \sqrt{18} = \sqrt{2 \times 3^2} \)
- Simplify: \( \sqrt{2 \times 3^2} = 3\sqrt{2} \)
So, \( \sqrt{18} \) simplifies to \( 3\sqrt{2} \).
Now, try to simplify the remaining problems on your own using the same steps. Check your answers below:
| Problem | Solution |
|---|---|
| \(\sqrt{50}\) | \(5\sqrt{2}\) |
| \(\sqrt{72}\) | \(6\sqrt{2}\) |
| \(\sqrt{98}\) | \(7\sqrt{2}\) |
| \(\sqrt{128}\) | \(8\sqrt{2}\) |
Keep practicing these steps with different numbers to get more comfortable with simplifying square roots. Happy solving!
Common Mistakes and How to Avoid Them
When simplifying square roots, such as √40, it's easy to make mistakes that can lead to incorrect results. Here are some common mistakes and tips on how to avoid them:
-
Overlooking Prime Factorization:
Skipping or incorrectly performing the prime factorization step can lead to an incorrect simplification. Ensure you find all prime factors of the number.
-
Ignoring Perfect Squares:
Not recognizing or extracting perfect squares from under the radical sign is a common error. Identify and factor out perfect squares to simplify the expression correctly.
-
Miscalculating Inside the Radical:
Errors in combining or separating terms under the radical can lead to incorrect results. Perform these operations accurately to maintain the correct value.
-
Misapplying Square Root Properties:
Misunderstanding the properties of square roots, such as \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \), can result in incorrect simplifications. Be sure to apply these properties correctly.
-
Forgetting to Simplify Completely:
Stopping the simplification process too early without combining all simplifiable elements under the radical sign can result in a less simplified form. Continue simplifying until you reach the simplest form.
Example: Simplifying √40
Let's go through the correct steps to simplify the square root of 40:
- Find the prime factorization of 40: \(40 = 2^3 \cdot 5\)
- Identify and extract the perfect square: \(2^2 = 4\)
- Rewrite the expression: \( \sqrt{40} = \sqrt{4 \cdot 10} = \sqrt{4} \cdot \sqrt{10} \)
- Simplify further: \( \sqrt{4} = 2 \), so \( \sqrt{40} = 2\sqrt{10} \)
By following these steps and avoiding common mistakes, you can ensure accurate and efficient simplification of square roots.
Hướng dẫn chi tiết về cách đơn giản hóa căn bậc hai của 40. Video này sẽ giúp bạn hiểu rõ và dễ dàng thực hiện các bước cần thiết.
Làm Thế Nào Để Đơn Giản Hóa Căn Bậc Hai Của 40: Sqrt(40)
READ MORE:
Xem video này để hiểu rõ cách phân tích căn bậc hai của số 40 và tìm hiểu các phương pháp đơn giản hóa.
Phân tích căn bậc hai của bốn mươi, sqrt(40)