Topic square root simplification problems: Welcome to our comprehensive guide on square root simplification problems! This article covers essential techniques and tips to simplify square roots efficiently. Whether you're a student, teacher, or math enthusiast, our guide will help you master this fundamental mathematical skill with clear explanations and practical examples.
Table of Content
- Simplifying Square Root Expressions
- Introduction to Square Root Simplification
- Basic Concepts of Square Root Simplification
- Prime Factorization Method for Simplifying Square Roots
- Pairing Prime Factors to Simplify Square Roots
- Simplifying Square Roots of Perfect Squares
- Simplifying Square Roots of Non-Perfect Squares
- Using the Quotient Property to Simplify Square Roots
- Examples of Simplifying Square Roots
- Step-by-Step Simplification of √12, √45, √72
- Simplifying Square Roots in Fractions
- Combining and Simplifying Multiple Square Roots
- Simplifying Expressions Involving Square Roots
- Advanced Square Root Simplification Problems
- Common Mistakes and How to Avoid Them
- Practice Problems for Square Root Simplification
- Real-World Applications of Square Root Simplification
- Conclusion and Further Reading
- YOUTUBE: Hướng dẫn chi tiết và dễ hiểu về cách đơn giản hóa căn bậc hai. Video phù hợp cho những ai đang tìm hiểu về bài toán đơn giản hóa căn bậc hai.
Simplifying Square Root Expressions
Simplifying square root expressions involves expressing the square root in its simplest form. This often means factoring the number under the square root into its prime factors and then simplifying.
Basic Steps to Simplify Square Roots
- Factor the number under the square root into its prime factors.
- Group the prime factors into pairs.
- Move each pair of prime factors outside the square root.
- Multiply the numbers outside the square root together.
- If there are any factors left under the square root, multiply them together inside the square root.
Examples
Example 1: Simplifying √12
12 can be factored into 4 × 3. Using the property of square roots, we get:
√12 = √(4 × 3) = √4 × √3 = 2√3
Example 2: Simplifying √45
45 can be factored into 9 × 5. Using the property of square roots, we get:
√45 = √(9 × 5) = √9 × √5 = 3√5
Example 3: Simplifying √72
72 can be factored into 36 × 2. Using the property of square roots, we get:
√72 = √(36 × 2) = √36 × √2 = 6√2
Fractions and Square Roots
The property of square roots can also be applied to fractions:
√(a/b) = √a / √b
Example: Simplifying √(27/16)
Using the property of square roots, we get:
√(27/16) = √27 / √16 = 3√3 / 4
Harder Examples
Example: Simplifying √20 × √5√2
First, we combine the numbers under one square root:
√20 × √5√2 = √(20 × 5 × 2) = √(200) = 10√2
Example: Simplifying 2√12 + 9√3
First simplify 2√12:
2√12 = 2 × 2√3 = 4√3
Now both terms have √3, so we can add them:
4√3 + 9√3 = (4+9)√3 = 13√3
Important Note
A root that cannot be simplified further is called a surd. For example, √3 is a surd, but √4 = 2 is not.

READ MORE:
Introduction to Square Root Simplification
Square root simplification involves reducing the expression under the radical sign to its simplest form. This process makes it easier to work with and understand square root values. The goal is to express the square root in a form where the number inside the radical is as small as possible while maintaining the same value. Here is a detailed guide to understanding and simplifying square roots step by step.
When simplifying square roots, the basic principle is to find the largest perfect square factor of the number under the square root and then rewrite the expression using this factor. The process can be summarized in the following steps:
- Factor the number inside the square root into its prime factors.
- Identify pairs of prime factors.
- Move each pair of prime factors outside the square root as a single number.
- Multiply the numbers outside the square root together and the numbers inside the square root together.
Let's look at a few examples to illustrate this process:
-
Example 1: Simplify \( \sqrt{12} \)
The factors of 12 are 4 and 3 (i.e., \( 12 = 4 \times 3 \)). Since 4 is a perfect square, we can rewrite the square root as:
\( \sqrt{12} = \sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3} = 2\sqrt{3} \) -
Example 2: Simplify \( \sqrt{45} \)
The factors of 45 are 9 and 5 (i.e., \( 45 = 9 \times 5 \)). Since 9 is a perfect square, we can rewrite the square root as:
\( \sqrt{45} = \sqrt{9 \times 5} = \sqrt{9} \times \sqrt{5} = 3\sqrt{5} \) -
Example 3: Simplify \( \sqrt{72} \)
The factors of 72 are 36 and 2 (i.e., \( 72 = 36 \times 2 \)). Since 36 is a perfect square, we can rewrite the square root as:
\( \sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2} \)
This method can also be applied to more complex expressions, including those involving variables or fractions. For instance, using the quotient property, the square root of a fraction can be expressed as the quotient of the square roots of the numerator and the denominator:
Example: Simplify \( \sqrt{\frac{18}{50}} \).
Rewrite the fraction under the square root: \( \sqrt{\frac{18}{50}} = \frac{\sqrt{18}}{\sqrt{50}} \).
Next, simplify each square root separately:
\( \sqrt{18} = 3\sqrt{2} \) (since 18 = 9 × 2 and √9 = 3),
\( \sqrt{50} = 5\sqrt{2} \) (since 50 = 25 × 2 and √25 = 5).
Thus, \( \sqrt{\frac{18}{50}} = \frac{3\sqrt{2}}{5\sqrt{2}} = \frac{3}{5} \).
With practice, simplifying square roots becomes an intuitive and useful skill in algebra and other areas of mathematics.
Basic Concepts of Square Root Simplification
Simplifying square roots involves reducing the number under the square root symbol (radicand) to its simplest form. Here are some basic concepts to help understand this process:
- Square Roots: The square root of a number \( x \) is a value that, when multiplied by itself, gives \( x \). For example, \( \sqrt{9} = 3 \) because \( 3 \times 3 = 9 \).
- Prime Factorization: This method involves breaking down the radicand into its prime factors. Prime numbers are numbers greater than 1 that have no divisors other than 1 and themselves. For instance, the prime factorization of 18 is \( 2 \times 3^2 \).
Step-by-Step Simplification Process
Here is a step-by-step guide to simplify square roots using prime factorization:
- Factor the number under the square root into its prime factors.
- Pair the prime factors. Each pair of the same number can be moved outside the square root as a single number.
- Multiply the numbers outside the square root and simplify any remaining numbers inside the square root.
Let's apply this process to simplify \( \sqrt{72} \):
- Step 1: Find the prime factorization of 72: \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \).
- Step 2: Pair the prime factors: \( (2 \times 2) \) and \( (3 \times 3) \). This can be written as \( \sqrt{2^3 \times 3^2} \).
- Step 3: Move the pairs outside the square root: \( 2 \times 3 \). We are left with \( \sqrt{2} \) inside the square root.
- Result: The simplified form is \( 6\sqrt{2} \).
Properties of Square Roots
Here are some useful properties of square roots to keep in mind:
- Product Property: \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \). For example, \( \sqrt{12} = \sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3} = 2\sqrt{3} \).
- Quotient Property: \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \). For instance, \( \sqrt{\frac{25}{9}} = \frac{\sqrt{25}}{\sqrt{9}} = \frac{5}{3} \).
By understanding and applying these basic concepts, you can simplify square roots effectively. Practice with different numbers to become more familiar with the process and properties.
Prime Factorization Method for Simplifying Square Roots
The prime factorization method is a systematic approach to simplifying square roots by breaking down a number into its prime factors. Here’s a detailed, step-by-step guide on how to use this method:
- Prime Factorization of the Number:
Start by expressing the number under the square root as a product of its prime factors. For example, to simplify √72:
\( 72 = 2 \times 2 \times 2 \times 3 \times 3 \) - Pair the Prime Factors:
Group the prime factors into pairs of the same number. Each pair will be used to simplify the square root.
\( 72 = (2 \times 2) \times (3 \times 3) \times 2 \) - Collect One Prime Factor from Each Pair:
Take one factor from each pair and multiply them together. Ignore the unpaired factors for now.
\( 2 \times 3 = 6 \) - Simplify the Expression:
The product of the factors taken from each pair is the simplified square root. Any unpaired factors remain under the square root.
\( \sqrt{72} = 6\sqrt{2} \)
Examples
| Number | Prime Factorization | Simplified Form |
|---|---|---|
| 16 | \( 2 \times 2 \times 2 \times 2 \) | \( \sqrt{16} = 4 \) |
| 81 | \( 3 \times 3 \times 3 \times 3 \) | \( \sqrt{81} = 9 \) |
| 100 | \( 2 \times 2 \times 5 \times 5 \) | \( \sqrt{100} = 10 \) |
By following these steps, you can simplify any square root using the prime factorization method. This method is particularly useful for larger numbers and ensures an accurate simplification process.
Pairing Prime Factors to Simplify Square Roots
Pairing prime factors is a crucial technique in simplifying square roots. This method involves expressing the number inside the square root (the radicand) as a product of prime factors and then grouping these factors into pairs. Each pair of prime factors can be simplified outside the square root.
Here's a step-by-step guide to simplify square roots using the pairing method:
- Start by performing the prime factorization of the radicand. Break down the number into its prime factors.
- Group the prime factors into pairs. Each pair represents a perfect square.
- Take the square root of each pair, which will bring one factor out of the square root.
- Multiply the factors that come out of the square root.
- Leave any unpaired prime factors inside the square root.
Let's look at some examples:
Example 1: Simplify √72
- Prime factorize 72: 72 = 2 × 2 × 2 × 3 × 3
- Group the factors into pairs: (2 × 2) and (3 × 3), with one 2 remaining
- Take the square root of each pair: √(2²) = 2 and √(3²) = 3
- Combine the results: 2 × 3 = 6
- So, √72 simplifies to 6√2
Example 2: Simplify √180
- Prime factorize 180: 180 = 2 × 2 × 3 × 3 × 5
- Group the factors into pairs: (2 × 2) and (3 × 3), with one 5 remaining
- Take the square root of each pair: √(2²) = 2 and √(3²) = 3
- Combine the results: 2 × 3 = 6
- So, √180 simplifies to 6√5
Example 3: Simplify √200
- Prime factorize 200: 200 = 2 × 2 × 2 × 5 × 5
- Group the factors into pairs: (2 × 2) and (5 × 5), with one 2 remaining
- Take the square root of each pair: √(2²) = 2 and √(5²) = 5
- Combine the results: 2 × 5 = 10
- So, √200 simplifies to 10√2
This method works well for any radicand, making it a reliable technique for simplifying square roots.

Simplifying Square Roots of Perfect Squares
Simplifying square roots of perfect squares is a straightforward process. A perfect square is a number that is the square of an integer. For instance, numbers like 1, 4, 9, 16, 25, and so on are perfect squares because they can be expressed as \(1^2\), \(2^2\), \(3^2\), \(4^2\), \(5^2\), etc. Here's a step-by-step guide on how to simplify the square roots of perfect squares:
-
Identify the perfect square: Determine if the number inside the square root is a perfect square. A perfect square has an integer as its square root. For example, \(16\) is a perfect square because \(4 \times 4 = 16\).
-
Find the square root: Calculate the square root of the perfect square. The square root of a perfect square is always an integer. For instance, \(\sqrt{16} = 4\).
-
Write the simplified form: Replace the square root of the perfect square with its integer value. For example, \(\sqrt{25} = 5\).
Here are a few examples to illustrate the process:
Example 1: Simplify \(\sqrt{64}\). Since \(64 = 8 \times 8\), it is a perfect square. Therefore, \(\sqrt{64} = 8\).
Example 2: Simplify \(\sqrt{81}\). Since \(81 = 9 \times 9\), it is a perfect square. Therefore, \(\sqrt{81} = 9\).
Example 3: Simplify \(\sqrt{144}\). Since \(144 = 12 \times 12\), it is a perfect square. Therefore, \(\sqrt{144} = 12\).
Simplifying square roots of perfect squares is a fundamental skill in algebra and helps in solving more complex mathematical problems efficiently.
Simplifying Square Roots of Non-Perfect Squares
To simplify square roots of non-perfect squares, we need to break down the number inside the square root (the radicand) into its prime factors and then pair the prime factors. Here's a step-by-step guide:
- Find the Prime Factorization:
Break down the radicand into its prime factors. For example, for √18:
- 18 = 2 × 3 × 3
- Pair the Prime Factors:
Group the prime factors into pairs. In our example:
- 18 = 2 × 3 × 3 = 3² × 2
- Simplify the Square Root:
Take one factor from each pair out of the square root. Any factors that are not paired stay inside. For √18:
- √(3² × 2) = 3√2
Let's look at more examples to clarify this process:
Examples:
- Example 1: Simplify √45
- Prime factorize 45: 45 = 3 × 3 × 5
- Group the pairs: 45 = 3² × 5
- Simplify: √(3² × 5) = 3√5
- Example 2: Simplify √72
- Prime factorize 72: 72 = 2 × 2 × 2 × 3 × 3
- Group the pairs: 72 = (2² × 3²) × 2
- Simplify: √(2² × 3² × 2) = 2 × 3√2 = 6√2
- Example 3: Simplify √200
- Prime factorize 200: 200 = 2 × 2 × 2 × 5 × 5
- Group the pairs: 200 = (2² × 5²) × 2
- Simplify: √(2² × 5² × 2) = 2 × 5√2 = 10√2
By following these steps, you can simplify any square root of a non-perfect square efficiently.
Using the Quotient Property to Simplify Square Roots
The Quotient Property of Square Roots states that the square root of a quotient is the same as the quotient of the square roots of the numerator and the denominator. This property can be very useful when simplifying square roots of fractions.
The property can be written as:
\[ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \]
Here’s a step-by-step guide on how to use the Quotient Property to simplify square roots:
- Simplify the fraction inside the radicand if possible.
- Rewrite the square root of the fraction as the quotient of the square roots of the numerator and the denominator.
- Simplify the square roots of the numerator and the denominator.
Let’s look at some examples:
Example 1: Simplify \( \sqrt{\frac{21}{64}} \)
- We cannot simplify the fraction \( \frac{21}{64} \) further.
- Rewrite using the quotient property: \( \frac{\sqrt{21}}{\sqrt{64}} \)
- Simplify the square roots: \( \frac{\sqrt{21}}{8} \)
Example 2: Simplify \( \sqrt{\frac{28}{81}} \)
- The fraction \( \frac{28}{81} \) cannot be simplified further.
- Rewrite using the quotient property: \( \frac{\sqrt{28}}{\sqrt{81}} \)
- Simplify the square roots: \( \frac{2\sqrt{7}}{9} \)
Example 3: Simplify \( \sqrt{\frac{45x^5}{y^4}} \)
- The fraction \( \frac{45x^5}{y^4} \) cannot be simplified further.
- Rewrite using the quotient property: \( \frac{\sqrt{45x^5}}{\sqrt{y^4}} \)
- Simplify the square roots: \( \frac{\sqrt{9x^4} \cdot \sqrt{5x}}{y^2} = \frac{3x^2\sqrt{5x}}{y^2} \)
By following these steps, you can simplify complex square root expressions involving fractions using the Quotient Property of Square Roots.
Examples of Simplifying Square Roots
Simplifying square roots involves expressing a square root in its simplest radical form. This often includes finding and factoring out perfect squares from the radicand (the number inside the square root). Here are some examples to illustrate the process:
Example 1: Simplify \(\sqrt{12}\)
- Identify perfect square factors: \(12 = 4 \times 3\).
- Write the square root as a product of square roots: \(\sqrt{12} = \sqrt{4 \times 3}\).
- Apply the product rule of square roots: \(\sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3}\).
- Simplify the perfect square: \(\sqrt{4} = 2\).
- Thus, \(\sqrt{12} = 2\sqrt{3}\).
Example 2: Simplify \(\sqrt{45}\)
- Identify perfect square factors: \(45 = 9 \times 5\).
- Write the square root as a product of square roots: \(\sqrt{45} = \sqrt{9 \times 5}\).
- Apply the product rule of square roots: \(\sqrt{9 \times 5} = \sqrt{9} \times \sqrt{5}\).
- Simplify the perfect square: \(\sqrt{9} = 3\).
- Thus, \(\sqrt{45} = 3\sqrt{5}\).
Example 3: Simplify \(\sqrt{72}\)
- Identify perfect square factors: \(72 = 36 \times 2\) (choosing the largest perfect square for fewer steps).
- Write the square root as a product of square roots: \(\sqrt{72} = \sqrt{36 \times 2}\).
- Apply the product rule of square roots: \(\sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2}\).
- Simplify the perfect square: \(\sqrt{36} = 6\).
- Thus, \(\sqrt{72} = 6\sqrt{2}\).
Example 4: Simplify \(\sqrt{180}\)
- Identify perfect square factors: \(180 = 36 \times 5\).
- Write the square root as a product of square roots: \(\sqrt{180} = \sqrt{36 \times 5}\).
- Apply the product rule of square roots: \(\sqrt{36 \times 5} = \sqrt{36} \times \sqrt{5}\).
- Simplify the perfect square: \(\sqrt{36} = 6\).
- Thus, \(\sqrt{180} = 6\sqrt{5}\).
Example 5: Simplify \(\sqrt{200}\)
- Identify perfect square factors: \(200 = 100 \times 2\).
- Write the square root as a product of square roots: \(\sqrt{200} = \sqrt{100 \times 2}\).
- Apply the product rule of square roots: \(\sqrt{100 \times 2} = \sqrt{100} \times \sqrt{2}\).
- Simplify the perfect square: \(\sqrt{100} = 10\).
- Thus, \(\sqrt{200} = 10\sqrt{2}\).
By breaking down the radicand into its prime factors or identifying the largest perfect square, we can simplify square roots efficiently. Practice these steps with different numbers to become more proficient in simplifying square roots.
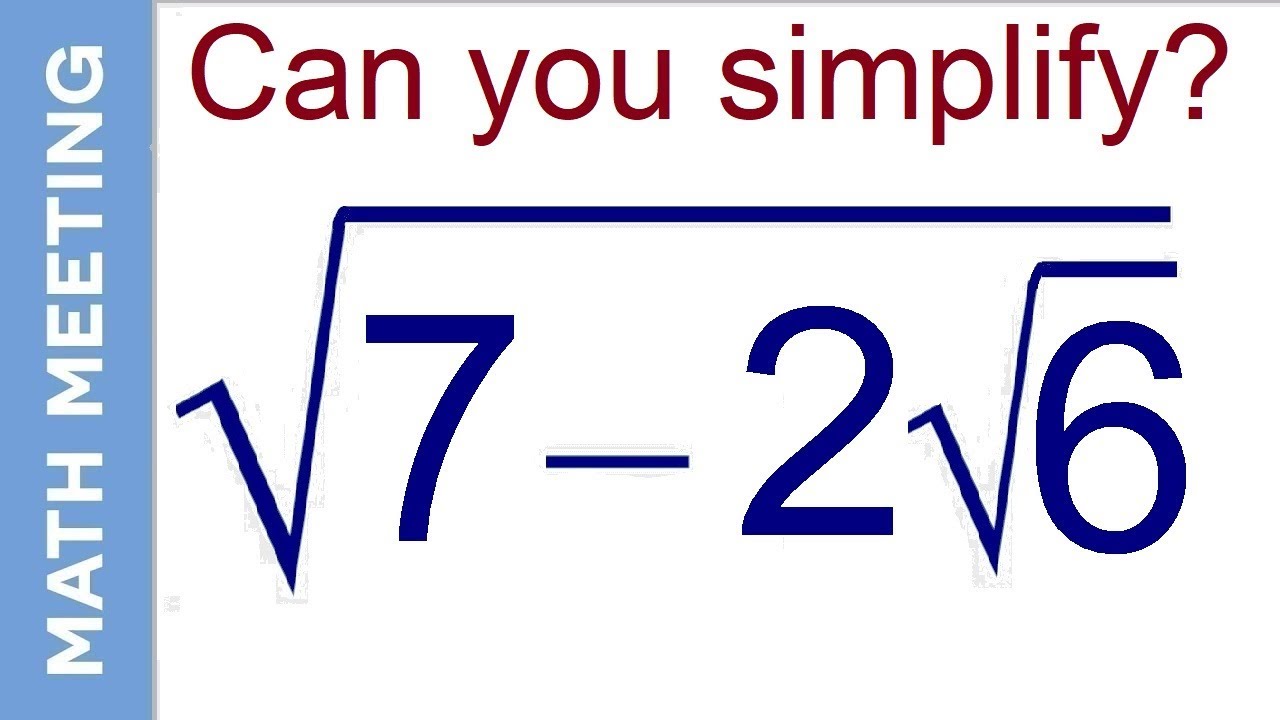
Step-by-Step Simplification of √12, √45, √72
To simplify square roots, we will use the prime factorization method. Let's take each example one by one:
Simplifying √12
- Find the prime factors of 12:
12 = 2 × 2 × 3
- Pair the prime factors:
(2 × 2) × 3
- Simplify the square root by taking one number from each pair out of the square root:
√(2² × 3) = 2√3
Simplifying √45
- Find the prime factors of 45:
45 = 3 × 3 × 5
- Pair the prime factors:
(3 × 3) × 5
- Simplify the square root by taking one number from each pair out of the square root:
√(3² × 5) = 3√5
Simplifying √72
- Find the prime factors of 72:
72 = 2 × 2 × 2 × 3 × 3
- Pair the prime factors:
(2 × 2) × (3 × 3) × 2
- Simplify the square root by taking one number from each pair out of the square root:
√(2² × 3² × 2) = 2 × 3 √2 = 6√2
By following these steps, you can simplify any square root. The key is to break down the number into its prime factors and then pair them to simplify the square root.
Simplifying Square Roots in Fractions
When simplifying square roots that appear in fractions, we can use the properties of radicals to make the process easier. Here's a step-by-step guide to simplify square roots in fractions:
Using the Quotient Rule
The quotient rule for square roots states that:
\(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
Using this rule, we can simplify square roots in fractions by separating the numerator and the denominator.
Examples
-
Simplify \(\sqrt{\frac{25}{36}}\)
- Apply the quotient rule: \(\sqrt{\frac{25}{36}} = \frac{\sqrt{25}}{\sqrt{36}}\)
- Simplify the square roots: \(\frac{\sqrt{25}}{\sqrt{36}} = \frac{5}{6}\)
- Therefore, \(\sqrt{\frac{25}{36}} = \frac{5}{6}\)
-
Simplify \(\sqrt{\frac{18}{50}}\)
- First, simplify the fraction inside the square root: \(\frac{18}{50} = \frac{9}{25}\)
- Apply the quotient rule: \(\sqrt{\frac{9}{25}} = \frac{\sqrt{9}}{\sqrt{25}}\)
- Simplify the square roots: \(\frac{\sqrt{9}}{\sqrt{25}} = \frac{3}{5}\)
- Therefore, \(\sqrt{\frac{18}{50}} = \frac{3}{5}\)
-
Simplify \(\sqrt{1 \frac{13}{36}}\)
- Convert the mixed number to an improper fraction: \(1 \frac{13}{36} = \frac{49}{36}\)
- Apply the quotient rule: \(\sqrt{\frac{49}{36}} = \frac{\sqrt{49}}{\sqrt{36}}\)
- Simplify the square roots: \(\frac{\sqrt{49}}{\sqrt{36}} = \frac{7}{6}\)
- Convert back to a mixed number: \(\frac{7}{6} = 1 \frac{1}{6}\)
- Therefore, \(\sqrt{1 \frac{13}{36}} = 1 \frac{1}{6}\)
Rationalizing the Denominator
Sometimes, after simplifying, the denominator may still contain a square root. In such cases, we can rationalize the denominator to remove the square root.
-
Simplify \(\frac{\sqrt{2}}{\sqrt{5}}\)
- Multiply the numerator and the denominator by \(\sqrt{5}\) to rationalize: \(\frac{\sqrt{2}}{\sqrt{5}} \times \frac{\sqrt{5}}{\sqrt{5}} = \frac{\sqrt{10}}{5}\)
- Therefore, \(\frac{\sqrt{2}}{\sqrt{5}} = \frac{\sqrt{10}}{5}\)
-
Simplify \(\frac{\sqrt{3}}{2\sqrt{7}}\)
- Multiply the numerator and the denominator by \(\sqrt{7}\) to rationalize: \(\frac{\sqrt{3}}{2\sqrt{7}} \times \frac{\sqrt{7}}{\sqrt{7}} = \frac{\sqrt{21}}{14}\)
- Therefore, \(\frac{\sqrt{3}}{2\sqrt{7}} = \frac{\sqrt{21}}{14}\)
By using these steps, you can simplify square roots in fractions and make your calculations easier and more manageable.
Combining and Simplifying Multiple Square Roots
When working with multiple square roots, there are several strategies you can use to combine and simplify them. Here we will discuss adding, subtracting, and multiplying square roots, illustrating each step with examples.
Adding and Subtracting Square Roots
To add or subtract square roots, the radicands (the numbers inside the square root) must be the same. Here are the steps:
- Simplify each square root individually.
- Combine the square roots that have the same radicand.
- Perform the addition or subtraction.
Example:
- Simplify \(3\sqrt{8} + 5\sqrt{2}\).
- First, simplify \(\sqrt{8}\) to \(2\sqrt{2}\).
- The expression becomes \(3(2\sqrt{2}) + 5\sqrt{2} = 6\sqrt{2} + 5\sqrt{2}\).
- Combine like terms: \(6\sqrt{2} + 5\sqrt{2} = 11\sqrt{2}\).
Multiplying Square Roots
To multiply square roots, use the product rule: \(\sqrt{a} \cdot \sqrt{b} = \sqrt{ab}\).
- Multiply the radicands together.
- Simplify the resulting square root if possible.
Example:
- Simplify \(\sqrt{12} \cdot \sqrt{3}\).
- Combine the radicands: \(\sqrt{12 \cdot 3} = \sqrt{36}\).
- Simplify \(\sqrt{36}\) to \(6\).
Combining Different Square Roots
Sometimes, you encounter expressions with different square roots. In such cases, simplify each square root and look for common factors.
Example:
- Simplify \(\sqrt{18} - 2\sqrt{27} + 3\sqrt{3} - 6\sqrt{8}\).
- Simplify each term:
- \(\sqrt{18} = \sqrt{9 \cdot 2} = 3\sqrt{2}\)
- \(2\sqrt{27} = 2\sqrt{9 \cdot 3} = 2(3\sqrt{3}) = 6\sqrt{3}\)
- \(\sqrt{27} = \sqrt{9 \cdot 3} = 3\sqrt{3}\)
- \(6\sqrt{8} = 6(2\sqrt{2}) = 12\sqrt{2}\)
- The expression now is \(3\sqrt{2} - 6\sqrt{3} + 3\sqrt{3} - 12\sqrt{2}\).
- Combine like terms: \((3\sqrt{2} - 12\sqrt{2}) + (3\sqrt{3} - 6\sqrt{3}) = -9\sqrt{2} - 3\sqrt{3}\).
By following these steps, you can simplify complex expressions involving multiple square roots.
Simplifying Expressions Involving Square Roots
When simplifying expressions involving square roots, it's important to follow specific rules and properties of square roots to ensure the expressions are simplified correctly. Below are steps and examples to help illustrate the process.
Basic Properties of Square Roots
- Product Property: \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \)
- Quotient Property: \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \) (where \( b \neq 0 \))
Steps to Simplify Expressions Involving Square Roots
- Simplify the expression inside the square root as much as possible.
- Apply the product and quotient properties of square roots where necessary.
- Simplify the resulting expression further if possible.
Examples
Example 1: Simplify \( \sqrt{50} \)
Steps:
- Factor the number inside the square root: \( \sqrt{50} = \sqrt{25 \cdot 2} \)
- Apply the product property: \( \sqrt{25 \cdot 2} = \sqrt{25} \cdot \sqrt{2} \)
- Simplify the square roots: \( \sqrt{25} = 5 \) and \( \sqrt{2} \) remains as it is.
- So, \( \sqrt{50} = 5\sqrt{2} \)
Example 2: Simplify \( \sqrt{\frac{81}{16}} \)
Steps:
- Apply the quotient property: \( \sqrt{\frac{81}{16}} = \frac{\sqrt{81}}{\sqrt{16}} \)
- Simplify the square roots: \( \sqrt{81} = 9 \) and \( \sqrt{16} = 4 \)
- So, \( \sqrt{\frac{81}{16}} = \frac{9}{4} \)
Example 3: Simplify \( \sqrt{45x^2} \)
Steps:
- Factor the number and the variable inside the square root: \( \sqrt{45x^2} = \sqrt{9 \cdot 5 \cdot x^2} \)
- Apply the product property: \( \sqrt{9 \cdot 5 \cdot x^2} = \sqrt{9} \cdot \sqrt{5} \cdot \sqrt{x^2} \)
- Simplify the square roots: \( \sqrt{9} = 3 \), \( \sqrt{x^2} = x \), and \( \sqrt{5} \) remains as it is.
- So, \( \sqrt{45x^2} = 3x\sqrt{5} \)
Example 4: Simplify \( \sqrt{18a^3b^4} \)
Steps:
- Factor the expression inside the square root: \( \sqrt{18a^3b^4} = \sqrt{9 \cdot 2 \cdot a^2 \cdot ab^4} \)
- Apply the product property: \( \sqrt{9 \cdot 2 \cdot a^2 \cdot ab^4} = \sqrt{9} \cdot \sqrt{2} \cdot \sqrt{a^2} \cdot \sqrt{a} \cdot \sqrt{b^4} \)
- Simplify the square roots: \( \sqrt{9} = 3 \), \( \sqrt{a^2} = a \), \( \sqrt{b^4} = b^2 \), and \( \sqrt{2} \) and \( \sqrt{a} \) remain as they are.
- So, \( \sqrt{18a^3b^4} = 3ab^2\sqrt{2a} \)
Tips for Simplifying Square Root Expressions
- Always look for perfect square factors within the radicand.
- Use the properties of square roots to break down complex expressions.
- Combine like terms and simplify where possible to achieve the most simplified form.
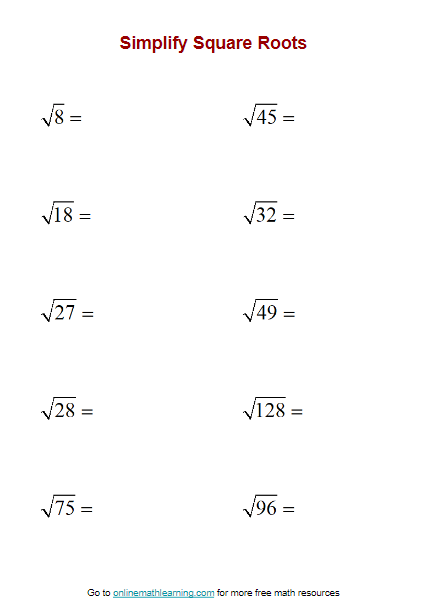
Advanced Square Root Simplification Problems
Advanced square root simplification problems often involve complex expressions, multiple variables, and higher powers. Here are step-by-step examples to help you master these challenges.
Example 1: Simplifying \(\sqrt[4]{16y^4}\)
We will use the property \(\sqrt[n]{a^n} = |a|\) when \(n\) is even.
- Rewrite the expression using the property:
\(\sqrt[4]{16y^4} = \sqrt[4]{2^4 y^4}\)
- Apply the product rule for radicals:
\(\sqrt[4]{2^4} \cdot \sqrt[4]{y^4} = 2 \cdot |y| = 2|y|\)
If variables are assumed to be positive, the result simplifies to \(2y\).
Example 2: Simplifying \(\sqrt{54a^{10}b^{16}c^7}\)
We will pair the variables and simplify the expression.
- Factorize the expression:
\(\sqrt{54 \cdot a^{10} \cdot b^{16} \cdot c^7} = \sqrt{3^3 \cdot 2 \cdot a^{10} \cdot b^{16} \cdot c^7}\)
- Group the terms into pairs:
\(\sqrt{3^2 \cdot 3 \cdot 2 \cdot (a^5)^2 \cdot (b^8)^2 \cdot (c^3)^2 \cdot c}\)
- Simplify the square roots:
\(3a^5b^8c^3\sqrt{6c}\)
Example 3: Denesting Radicals
Denesting involves rewriting nested radicals into simpler forms. Let's simplify \(\sqrt{2 + \sqrt{3}}\).
- Assume \(\sqrt{2 + \sqrt{3}} = \sqrt{x} + \sqrt{y}\).
Square both sides: \(2 + \sqrt{3} = x + y + 2\sqrt{xy}\).
- Set the rational parts equal:
\(x + y = 2\)
- Set the irrational parts equal:
\(\sqrt{3} = 2\sqrt{xy} \rightarrow xy = \frac{3}{4}\).
- Solve for \(x\) and \(y\):
Using \(x + y = 2\) and \(xy = \frac{3}{4}\), solve the quadratic equation: \(t^2 - 2t + \frac{3}{4} = 0\).
- Find the roots:
The solutions are \(x = \frac{3}{2}\) and \(y = \frac{1}{2}\).
- Thus,
\(\sqrt{2 + \sqrt{3}} = \sqrt{\frac{3}{2}} + \sqrt{\frac{1}{2}}\).
Example 4: Simplifying Complex Expressions
Simplify \(\sqrt{\frac{18a^5}{b^8}}\).
- Factorize the expression:
\(\sqrt{\frac{2 \cdot 3^2 \cdot a^5}{(b^4)^2}} = \frac{\sqrt{2} \cdot \sqrt{3^2} \cdot \sqrt{a^5}}{b^4}\)
- Simplify the square roots:
\(\frac{3a^2\sqrt{2a}}{b^4}\)
Advanced problems like these require practice and familiarity with various properties of square roots and radicals. By mastering these steps, you can confidently tackle more challenging expressions.
Common Mistakes and How to Avoid Them
Simplifying square roots can be tricky, and it's common to make mistakes along the way. Here are some frequent errors and tips on how to avoid them:
-
Ignoring the Properties of Square Roots:
A common mistake is overlooking basic properties such as \( \sqrt{ab} = \sqrt{a} \cdot \sqrt{b} \). Always apply these properties correctly to simplify expressions effectively.
-
Incorrect Prime Factorization:
Incorrectly factoring a number into its prime factors can lead to wrong simplifications. To avoid this, double-check your factorization. Using a factor tree can help visualize and verify the process.
-
Overlooking Perfect Squares:
Missing perfect squares within a radical can complicate simplification unnecessarily. Familiarize yourself with the list of perfect squares to quickly identify and extract them from under the radical.
-
Misapplying Negative Signs:
Misunderstanding how to handle negative signs with square roots, especially with imaginary numbers, can lead to errors. Remember that \( \sqrt{-a} \) is not the same as \( -\sqrt{a} \). The former indicates an imaginary number, while the latter does not.
-
Incorrectly Simplifying Fractions:
When simplifying square roots of fractions, remember to simplify the numerator and denominator separately. For example, \( \sqrt{\frac{4}{9}} = \frac{\sqrt{4}}{\sqrt{9}} = \frac{2}{3} \).
-
Combining Unlike Radicals:
Ensure that you only combine like radicals. For instance, \( 2\sqrt{3} + 4\sqrt{3} = 6\sqrt{3} \), but \( 2\sqrt{2} + 3\sqrt{3} \) cannot be combined since the radicals are different.
-
Not Rationalizing the Denominator:
Leaving a square root in the denominator is typically avoided in final answers. Rationalize the denominator by multiplying both the numerator and the denominator by the conjugate if necessary. For example, \( \frac{1}{\sqrt{2}} \) should be simplified to \( \frac{\sqrt{2}}{2} \).
By keeping these common mistakes in mind and practicing regularly, you can improve your skills in simplifying square roots.
Practice Problems for Square Root Simplification
Practicing square root simplification helps in mastering the concept. Here are several problems to practice, along with step-by-step solutions:
Example Problems:
-
Simplify \( \sqrt{50} \)
Solution:
- Prime factorize 50: \( 50 = 2 \times 5^2 \)
- Apply the square root: \( \sqrt{50} = \sqrt{2 \times 5^2} = 5\sqrt{2} \)
-
Simplify \( \sqrt{72} \)
Solution:
- Prime factorize 72: \( 72 = 2^3 \times 3^2 \)
- Apply the square root: \( \sqrt{72} = \sqrt{2^3 \times 3^2} = 3\sqrt{8} = 3 \times 2\sqrt{2} = 6\sqrt{2} \)
-
Simplify \( \sqrt{128} \)
Solution:
- Prime factorize 128: \( 128 = 2^7 \)
- Apply the square root: \( \sqrt{128} = \sqrt{2^7} = \sqrt{2^6 \times 2} = 2^3 \sqrt{2} = 8\sqrt{2} \)
Fractional Square Root Problems:
-
Simplify \( \sqrt{\frac{9}{16}} \)
Solution:
- Simplify numerator and denominator separately: \( \sqrt{\frac{9}{16}} = \frac{\sqrt{9}}{\sqrt{16}} = \frac{3}{4} \)
-
Simplify \( \sqrt{\frac{18}{50}} \)
Solution:
- Simplify the fraction inside the square root: \( \frac{18}{50} = \frac{9}{25} \)
- Simplify numerator and denominator separately: \( \sqrt{\frac{9}{25}} = \frac{\sqrt{9}}{\sqrt{25}} = \frac{3}{5} \)
By practicing these problems regularly, you can enhance your understanding and proficiency in simplifying square roots.
Real-World Applications of Square Root Simplification
Square root simplification is not just an academic exercise; it has several practical applications in various fields. Here are some real-world scenarios where square roots play a crucial role:
1. Geometry and Construction
In geometry, square roots are used to find the lengths of sides in right triangles, especially when applying the Pythagorean theorem. For instance, in construction, determining the diagonal length of a rectangular object requires calculating the square root of the sum of the squares of its sides.
Example:
- To find the length of the diagonal of a rectangle with sides of length 3 feet and 4 feet:
- \(\sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5\) feet
2. Distance Calculations
Square roots are essential in calculating distances between points in both two-dimensional and three-dimensional spaces, which is vital in fields like navigation, cartography, and even video game development.
Example:
- To find the distance between points \((1, 2)\) and \((4, 6)\) in a plane:
- \(\sqrt{(4 - 1)^2 + (6 - 2)^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5\)
3. Physics and Engineering
In physics, the concept of square roots is used in various formulas, such as calculating the period of a pendulum, determining escape velocity, and understanding wave functions. Engineers often use square roots when dealing with stress and strain in materials.
Example:
- The time \( t \) it takes for an object to fall from a height \( h \) is given by \( t = \sqrt{\frac{2h}{g}} \), where \( g \) is the acceleration due to gravity.
- For \( h = 45 \) meters and \( g = 9.8 \, \text{m/s}^2 \):
- \( t = \sqrt{\frac{2 \times 45}{9.8}} = \sqrt{9.18} \approx 3.03 \, \text{seconds} \)
4. Financial Calculations
In finance, square roots are used to compute compound interest and depreciation. For example, the formula for calculating the compound interest involves taking the nth root of the amount, which essentially involves using square roots and other radicals.
Example:
- To find the compound interest for an amount \( P \) after \( n \) years at an annual interest rate \( r \), the formula is:
- \( A = P \left(1 + \frac{r}{n}\right)^{nt} \)
5. Biology and Medicine
In biology, square roots help in understanding various phenomena, such as the rate of diffusion of substances and the scaling laws in biology, which describe how different characteristics of organisms change with size. Medical professionals also use square roots in imaging techniques and understanding dosages based on body surface area.
Example:
- To calculate the body surface area \( BSA \) for medical dosages, one common formula is:
- \( BSA = \sqrt{\left(\frac{height \, (cm) \times weight \, (kg)}{3600}\right)} \)
These examples highlight the importance of understanding and simplifying square roots, as they provide critical insights and solutions in real-world problems.

Conclusion and Further Reading
Square root simplification is a fundamental skill in algebra that not only enhances problem-solving abilities but also lays the groundwork for more advanced mathematical concepts. By mastering techniques such as prime factorization, pairing factors, and utilizing properties like the quotient property, you can simplify square roots with ease and confidence.
Throughout this guide, we've covered a variety of methods and examples to help you understand and practice simplifying square roots. Whether dealing with perfect squares, non-perfect squares, or square roots in fractions, the key is to break down the problem into manageable steps and apply the appropriate rules and properties.
For further reading and more in-depth practice, consider exploring the following resources:
- : Offers video lessons and practice problems to reinforce your understanding.
- : Provides step-by-step explanations and examples to help you master the topic.
- : Features detailed tutorials and video lessons on various methods for simplifying square roots.
- : An excellent tool for checking your work and exploring additional problems.
- : Offers comprehensive lessons on radicals and their simplification.
With these resources, you can continue to practice and deepen your understanding of square root simplification. Keep challenging yourself with new problems, and soon you'll find that simplifying square roots becomes second nature.
Hướng dẫn chi tiết và dễ hiểu về cách đơn giản hóa căn bậc hai. Video phù hợp cho những ai đang tìm hiểu về bài toán đơn giản hóa căn bậc hai.
Cách Đơn Giản Hóa Căn Bậc Hai
READ MORE:
Hướng dẫn của Math Antic về cách đơn giản hóa các căn bậc hai.
Math Antic - Đơn Giản Hóa Căn Bậc Hai















