Topic square root of 1-20: Discover the fundamentals and methods for calculating the square roots of numbers from 1 to 20. This article provides a detailed explanation of various techniques such as prime factorization, long division, and estimation. Gain a deeper understanding of both perfect and non-perfect squares with practical examples and useful tips.
Table of Content
Square Root of Numbers from 1 to 20
The square roots of the numbers from 1 to 20 are important in various mathematical calculations. Below is a detailed table and explanations on how to calculate and understand square roots.
Table of Square Roots from 1 to 20
| Number | Square Root |
|---|---|
| 1 | \(\sqrt{1} = 1\) |
| 2 | \(\sqrt{2} \approx 1.414\) |
| 3 | \(\sqrt{3} \approx 1.732\) |
| 4 | \(\sqrt{4} = 2\) |
| 5 | \(\sqrt{5} \approx 2.236\) |
| 6 | \(\sqrt{6} \approx 2.449\) |
| 7 | \(\sqrt{7} \approx 2.646\) |
| 8 | \(\sqrt{8} \approx 2.828\) |
| 9 | \(\sqrt{9} = 3\) |
| 10 | \(\sqrt{10} \approx 3.162\) |
| 11 | \(\sqrt{11} \approx 3.317\) |
| 12 | \(\sqrt{12} \approx 3.464\) |
| 13 | \(\sqrt{13} \approx 3.606\) |
| 14 | \(\sqrt{14} \approx 3.742\) |
| 15 | \(\sqrt{15} \approx 3.873\) |
| 16 | \(\sqrt{16} = 4\) |
| 17 | \(\sqrt{17} \approx 4.123\) |
| 18 | \(\sqrt{18} \approx 4.243\) |
| 19 | \(\sqrt{19} \approx 4.359\) |
| 20 | \(\sqrt{20} \approx 4.472\) |
Methods to Calculate Square Roots
-
Prime Factorization
This method involves breaking down a number into its prime factors and then pairing the factors to find the square root.
-
Long Division Method
Used for non-perfect squares, this method involves dividing the number into smaller, manageable steps to approximate the square root.
Examples
-
Find the square root of 4:
Prime factorization of 4 is \(2 \times 2\). Therefore, \(\sqrt{4} = 2\).
-
Find the square root of 15:
Using estimation, \(\sqrt{15} \approx 3.873\).
Applications
Square roots are used in various fields such as geometry, physics, and engineering. For example, to find the side length of a square with an area of 11 sq. inches, you calculate \(\sqrt{11} \approx 3.317\) inches.
FAQs
- What is the square root of 16? The square root of 16 is 4.
- How many numbers between 1 and 20 have irrational square roots? The numbers 2, 3, 5, 6, 7, 8, 10, 11, 12, 13, 14, 15, 17, 18, 19, and 20 have irrational square roots.

READ MORE:
Introduction to Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 16 is 4, because 4 x 4 = 16. Square roots can be positive or negative, but the principal square root is the non-negative value.
Mathematically, if \( y \) is the square root of \( x \), then \( y^2 = x \). This is represented as \( \sqrt{x} = y \). For instance, \( \sqrt{25} = 5 \) because \( 5^2 = 25 \).
Square roots of numbers between 1 and 20 include both rational and irrational numbers. Rational numbers have exact square roots, while irrational numbers have non-terminating, non-repeating decimals. For example, \( \sqrt{4} = 2 \) is rational, and \( \sqrt{2} \approx 1.414 \) is irrational.
Understanding square roots is fundamental in various mathematical applications, including solving quadratic equations, calculating areas, and working with complex numbers.
Basic Concepts
The square root of a number is a value that, when multiplied by itself, gives the original number. The square root is denoted by the symbol \(\sqrt{}\). For instance, \(\sqrt{9} = 3\) because \(3 \times 3 = 9\). Understanding square roots involves recognizing perfect squares and approximating non-perfect squares.
- Perfect Squares: Numbers like 1, 4, 9, 16, etc., are perfect squares because their square roots are whole numbers.
- Imperfect Squares: Numbers like 2, 3, 5, etc., are imperfect squares as their square roots are not whole numbers.
Let's explore some methods to calculate square roots:
- Prime Factorization:
- Decompose the number into prime factors.
- Pair the prime factors.
- Multiply one number from each pair.
- Example: \(\sqrt{144}\) = 12 as \(144 = 2^4 \times 3^2\).
- Repeated Subtraction:
- Subtract consecutive odd numbers starting from 1.
- Example: \(\sqrt{9}\) = 3 as \(9 - 1 - 3 - 5 = 0\).
- Estimation:
- Identify the nearest perfect squares.
- Narrow down the range by squaring numbers in between.
- Example: \(\sqrt{15}\) is between 3.8 and 3.9.
Using these methods, one can find the square roots of both perfect and imperfect squares effectively. Memorizing the square root values of numbers from 1 to 20 can also be helpful.
| Number | Square Root |
|---|---|
| 1 | 1 |
| 2 | 1.414 |
| 3 | 1.732 |
| 4 | 2 |
| 5 | 2.236 |
| 6 | 2.449 |
| 7 | 2.646 |
| 8 | 2.828 |
| 9 | 3 |
| 10 | 3.162 |
| 11 | 3.317 |
| 12 | 3.464 |
| 13 | 3.606 |
| 14 | 3.742 |
| 15 | 3.873 |
| 16 | 4 |
| 17 | 4.123 |
| 18 | 4.243 |
| 19 | 4.359 |
| 20 | 4.472 |
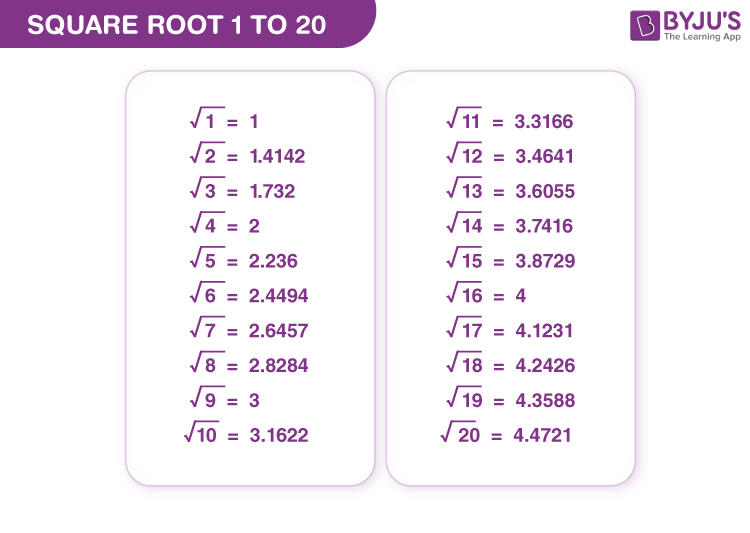
Square Root Chart (1 to 20)
Understanding square roots is essential in various branches of mathematics including algebra, geometry, and statistics. Below is a detailed chart listing the square roots of numbers from 1 to 20, presented in a clear and comprehensive manner.
| Number | Square Root |
|---|---|
| 1 | \(\sqrt{1} = 1\) |
| 2 | \(\sqrt{2} \approx 1.414\) |
| 3 | \(\sqrt{3} \approx 1.732\) |
| 4 | \(\sqrt{4} = 2\) |
| 5 | \(\sqrt{5} \approx 2.236\) |
| 6 | \(\sqrt{6} \approx 2.449\) |
| 7 | \(\sqrt{7} \approx 2.646\) |
| 8 | \(\sqrt{8} \approx 2.828\) |
| 9 | \(\sqrt{9} = 3\) |
| 10 | \(\sqrt{10} \approx 3.162\) |
| 11 | \(\sqrt{11} \approx 3.317\) |
| 12 | \(\sqrt{12} \approx 3.464\) |
| 13 | \(\sqrt{13} \approx 3.606\) |
| 14 | \(\sqrt{14} \approx 3.742\) |
| 15 | \(\sqrt{15} \approx 3.873\) |
| 16 | \(\sqrt{16} = 4\) |
| 17 | \(\sqrt{17} \approx 4.123\) |
| 18 | \(\sqrt{18} \approx 4.243\) |
| 19 | \(\sqrt{19} \approx 4.359\) |
| 20 | \(\sqrt{20} \approx 4.472\) |
Memorizing these square roots can greatly assist in quick mental calculations and problem-solving in various mathematical contexts. For more complex calculations, especially those involving non-perfect squares, approximation methods or calculators are often used to achieve the necessary precision.
Examples and Solved Problems
Understanding square roots involves practicing with examples and solving problems. Here are a few detailed examples to help you grasp the concept better.
Example 1: Find the square root of 16 using the repeated subtraction method
The repeated subtraction method involves subtracting successive odd numbers from the given number until we reach zero. The number of steps taken gives the square root.
- 16 - 1 = 15
- 15 - 3 = 12
- 12 - 5 = 7
- 7 - 7 = 0
Since we reached zero in the 4th step, the square root of 16 is 4.
Example 2: Calculate the value of \(17\sqrt{9} + 12\sqrt{25}\)
First, find the square roots of 9 and 25:
- \(\sqrt{9} = 3\)
- \(\sqrt{25} = 5\)
Now, substitute these values into the expression:
\(17\sqrt{9} + 12\sqrt{25} = 17 \times 3 + 12 \times 5 = 51 + 60 = 111\)
So, \(17\sqrt{9} + 12\sqrt{25} = 111\).
Example 3: Determine the radius of a circular tabletop with an area of \(19\pi\) square inches
The area \(A\) of a circle is given by the formula \(A = \pi r^2\), where \(r\) is the radius.
Given \(A = 19\pi\):
\(19\pi = \pi r^2\)
Dividing both sides by \(\pi\):
19 = \(r^2\)
Taking the square root of both sides:
\(r = \sqrt{19} \approx 4.36\)
Therefore, the radius of the tabletop is approximately 4.36 inches.
Example 4: Solve for \(x\) in the equation \(x^2 = 64\)
We know that \(8^2 = 64\), hence:
\(x^2 = 64\)
Taking the square root of both sides:
\(x = \sqrt{64} = 8\)
Thus, \(x = 8\).
Example 5: Simplify \( \sqrt{16} + \sqrt{25}\)
First, find the square roots:
- \(\sqrt{16} = 4\)
- \(\sqrt{25} = 5\)
Now, add these values:
\(\sqrt{16} + \sqrt{25} = 4 + 5 = 9\)
Therefore, \( \sqrt{16} + \sqrt{25} = 9\).
Applications of Square Roots
Square roots are widely used in various fields and everyday situations. Here are some key applications:
- Geometry and Trigonometry: Square roots are essential in calculating the lengths of sides in right-angled triangles using the Pythagorean theorem. For instance, if one leg of a right triangle is 3 and the other is 4, the hypotenuse is calculated as \( \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \).
- Physics: Square roots appear in many physical formulas, such as calculating the root mean square (RMS) velocity of gas particles, which is given by \( v_{\text{RMS}} = \sqrt{\frac{3kT}{m}} \), where \( k \) is the Boltzmann constant, \( T \) is the temperature, and \( m \) is the mass of a particle.
- Engineering: In engineering, square roots are used to determine the stress and strain on materials, electrical properties in circuits, and fluid dynamics. For example, in electrical engineering, the RMS value of an alternating current (AC) is calculated using the square root.
- Finance: In finance, square roots are used in various calculations, such as determining the standard deviation of investment returns, which measures volatility. The formula for standard deviation is \( \sigma = \sqrt{\frac{1}{N}\sum_{i=1}^{N}(x_i - \mu)^2} \), where \( N \) is the number of observations, \( x_i \) are the observed values, and \( \mu \) is the mean.
- Astronomy: In astronomy, square roots are used to calculate distances between celestial objects and their movements. For example, the formula for the escape velocity from a planet is \( v_e = \sqrt{\frac{2GM}{r}} \), where \( G \) is the gravitational constant, \( M \) is the mass of the planet, and \( r \) is the radius from the center of the planet.
- Computer Graphics: Square roots are used in computer graphics for calculating distances, lighting effects, and rendering 3D models. For instance, the Euclidean distance between two points in 3D space is calculated using the formula \( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2} \).
Historical Context
The concept of square roots has a rich history that dates back to ancient civilizations. Here are some significant milestones in the development and understanding of square roots:
- Babylonian Mathematics:
The Babylonians were among the first to estimate square roots. The clay tablet YBC 7289, dating between 1800 BC and 1600 BC, shows an approximation of √2 accurate to five decimal places.
- Egyptian Mathematics:
In ancient Egypt, the Rhind Mathematical Papyrus (circa 1650 BC) demonstrates methods for calculating square roots using inverse proportion techniques.
- Ancient India:
Indian mathematicians made significant contributions to the study of square roots. The Sulba Sutras (circa 800-500 BC) include methods for approximating square roots. Notably, Aryabhata's Aryabhatiya (499 AD) provides techniques for extracting square roots of large numbers.
- Greek Mathematics:
The ancient Greeks explored the properties of square roots extensively. They proved that the square roots of non-perfect squares are irrational numbers. This discovery is attributed to the Pythagorean school and Euclid's Elements.
- Chinese Mathematics:
In the Han dynasty (202 BC - 220 AD), Chinese mathematicians approximated square roots using an "excess and deficiency" method. This is documented in the "Writings on Reckoning."
- Medieval Islamic Mathematics:
Arab mathematicians used the letter jīm (ج) to denote square roots. This notation was used extensively in the works of scholars like Al-Khwarizmi and Ibn al-Yasamin.
- Renaissance Europe:
The symbol √ for the square root was first used in print by Christoph Rudolff in 1525. This period saw a revival of interest in ancient mathematical texts and further advancements in the understanding of square roots.
Understanding the Square Root Function
The square root function is a fundamental mathematical concept that provides the value that, when multiplied by itself, gives the original number. This function is denoted by the radical symbol \(\sqrt{}\). For any non-negative number \(a\), the square root of \(a\) is a number \(x\) such that \(x^2 = a\).
Here are the key properties and aspects of the square root function:
- Principal Square Root: The non-negative square root of a non-negative number is known as the principal square root. For example, \(\sqrt{16} = 4\) since \(4^2 = 16\).
- Positive and Negative Roots: Every positive number has two square roots: one positive and one negative. For instance, \(\sqrt{25} = 5\) and \(-\sqrt{25} = -5\) because both \(5^2\) and \((-5)^2\) equal 25.
- Perfect Squares: Numbers like 1, 4, 9, 16, etc., whose square roots are integers, are called perfect squares. The square roots of non-perfect squares are irrational numbers.
- Domain and Range: The domain of the square root function is the set of non-negative real numbers \([0, \infty)\), and its range is also the set of non-negative real numbers \([0, \infty)\).
The square root function can be represented graphically. The graph of \(y = \sqrt{x}\) is a curve that starts at the origin (0,0) and increases slowly as \(x\) increases. It is important to note that the function \(y = \sqrt{x}\) is defined only for \(x \geq 0\).
Mathematical Representation
The square root of a number \(x\) can be mathematically represented as:
\[
\sqrt{x} = x^{1/2}
\]
For example:
- \(\sqrt{9} = 3\) because \(3^2 = 9\)
- \(\sqrt{20} \approx 4.47\) because \(4.47^2 \approx 20\)
Calculating Square Roots
There are several methods to calculate square roots:
- Prime Factorization: Break down the number into its prime factors and pair the factors. The product of one element from each pair is the square root. For example, \(\sqrt{36}\) is calculated by breaking 36 into prime factors \(2 \times 2 \times 3 \times 3\) and then taking one element from each pair, resulting in \(2 \times 3 = 6\).
- Long Division Method: This manual method involves pairing the digits from right to left, finding the largest square smaller than the first pair, and iterating through a division-like process to get the root.
Applications of Square Roots
Square roots have numerous applications in various fields such as architecture, finance, physics, engineering, and computer graphics. They are essential in solving quadratic equations, determining distances, calculating areas, and analyzing data variability, among other uses.
Understanding the square root function and its properties is crucial for tackling more advanced mathematical concepts and real-world problems efficiently.
Approximations and Calculations
Calculating the square root of a number can be performed through various methods, each with different levels of precision and complexity. Here, we explore several common techniques for approximating and calculating square roots, particularly for numbers between 1 and 20.
1. Estimation Method
The estimation method involves finding two perfect squares between which the number lies. For example, to approximate the square root of 15:
- Identify the two closest perfect squares: 9 (32) and 16 (42).
- The square root of 15 will be between 3 and 4.
- Estimate by averaging: (3.8)2 ≈ 14.44, which is close to 15.
2. Long Division Method
This method provides a more accurate value by performing a digit-by-digit calculation, similar to long division:
- Separate the number into pairs of digits, starting from the decimal point.
- Find the largest number whose square is less than or equal to the first pair.
- Use this number to perform the division and continue with subsequent pairs.
For example, for √18:
| 1 | . | 3 | 4 |
| ____________ | |||
| 1 | 8 | 00 | |
| 1 | |||
The result is approximately 4.24.
3. Newton's Method (Iterative Approximation)
Newton's method, also known as the Newton-Raphson method, uses an iterative approach to refine the approximation:
- Start with an initial guess \( x_0 \).
- Use the formula: \( x_{n+1} = \frac{1}{2} (x_n + \frac{S}{x_n}) \), where S is the number you are finding the square root of.
- Repeat until the desired precision is achieved.
For example, to find √2:
- Start with \( x_0 = 1 \).
- Calculate \( x_1 = \frac{1}{2} (1 + \frac{2}{1}) = 1.5 \).
- Continue iterations: \( x_2 = \frac{1}{2} (1.5 + \frac{2}{1.5}) \approx 1.4167 \), and so on.
4. Binomial Expansion
The binomial expansion can be used for numbers close to a perfect square. For example, to approximate √1.1:
Using the formula \( \sqrt{1 + x} \approx 1 + \frac{x}{2} - \frac{x^2}{8} + \frac{x^3}{16} - ... \):
For \( \sqrt{1.1} \), \( x = 0.1 \):
- \( \sqrt{1.1} \approx 1 + \frac{0.1}{2} - \frac{(0.1)^2}{8} \)
- \( \approx 1 + 0.05 - 0.00125 = 1.04875 \)
This provides a good approximation.
These methods offer different balances between simplicity and precision, making them suitable for various applications from quick mental calculations to more rigorous mathematical computations.

Simplifying Square Roots
Square roots can often be simplified to make calculations easier and to express the number in a more manageable form. Simplifying square roots involves factoring the number under the square root into its prime factors and then simplifying based on pairs of prime factors.
Here are the steps to simplify square roots:
- Find the prime factors: Break down the number under the square root into its prime factors. For example, to simplify \(\sqrt{72}\), first find its prime factors: \(72 = 2 \times 2 \times 2 \times 3 \times 3\).
- Group the prime factors: Pair the prime factors. In our example, we have pairs of 2s and 3s: \((2 \times 2) \times (3 \times 3) \times 2\).
- Take out the pairs: For each pair, take one factor out of the square root. Thus, \(\sqrt{72} = \sqrt{(2 \times 2) \times (3 \times 3) \times 2} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2}\).
Examples
- Simplifying \(\sqrt{50}\):
- Prime factorize 50: \(50 = 2 \times 5 \times 5\)
- Group the prime factors: \( \sqrt{(5 \times 5) \times 2} \)
- Simplify: \( 5\sqrt{2} \)
- Simplifying \(\sqrt{18}\):
- Prime factorize 18: \(18 = 2 \times 3 \times 3\)
- Group the prime factors: \( \sqrt{(3 \times 3) \times 2} \)
- Simplify: \( 3\sqrt{2} \)
Simplifying Variables with Square Roots
Square roots can also involve variables. For example, to simplify \(\sqrt{50x^2}\), you would:
- Prime factorize the number: \(50 = 2 \times 5 \times 5\)
- Include the variable: \( \sqrt{(5 \times 5) \times 2 \times x^2} \)
- Simplify: \( 5x\sqrt{2} \)
Important Considerations
- Always look for the largest perfect square factor of the number to simplify the square root more efficiently.
- Remember that every positive number has two square roots: one positive and one negative. However, the principal square root (denoted by the radical sign) is always the positive root.
- Simplifying square roots with variables requires ensuring the variable under the square root is non-negative to keep the expression within the realm of real numbers.
By practicing these steps, you can efficiently simplify square roots, making it easier to work with these numbers in various mathematical problems and applications.
Mẹo tính nhanh bình phương và căn bậc hai từ 11 đến 20 - Thủ thuật Toán học
READ MORE:
Căn bậc hai và căn bậc ba của các số từ 1 đến 20 / Cách viết căn bậc hai và căn bậc ba của các số từ 1 đến 20