Topic 4 square root of 6: Explore the fascinating world of the mathematical expression 4 square root of 6. Discover its calculation, applications in various fields, and its significance in both academic and real-world contexts. This guide provides a clear and detailed understanding of how to simplify and utilize 4 √6 effectively.
Table of Content
- Calculating and Understanding the Expression: 4 √6
- Introduction to Square Roots
- Understanding the Expression 4 √6
- Calculating 4 √6
- Approximation and Exact Values
- Step-by-Step Calculation
- Mathematical Properties of √6
- Applications in Algebra
- Applications in Geometry
- Applications in Trigonometry
- Importance in Mathematical Context
- Real-World Examples
- Common Mistakes and Misconceptions
- Practice Problems and Solutions
- Advanced Topics Related to Square Roots
- Conclusion
- YOUTUBE: Khám phá cách tính căn bậc hai của 6 với ví dụ minh họa và giải thích chi tiết. Học cách áp dụng trong các bài toán thực tế.
Calculating and Understanding the Expression: 4 √6
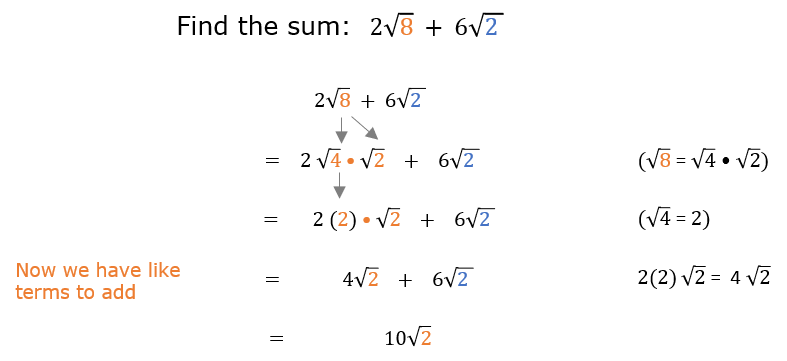
The expression involves a multiplication of 4 with the square root of 6. This can be represented mathematically as:
Steps to Simplify and Calculate
- Identify the square root component:
- Multiply 4 by the approximate value of the square root of 6:
The square root of 6 is an irrational number, approximately equal to 2.44949.
Detailed Calculation
The exact value of is:
Using in Mathematical Context
- Algebra: Simplifies to help in solving equations.
- Geometry: Useful in calculations involving distances and areas.
- Trigonometry: Appears in various trigonometric functions and identities.
Understanding the expression helps in various fields of mathematics, providing a solid foundation for more complex calculations and applications.

READ MORE:
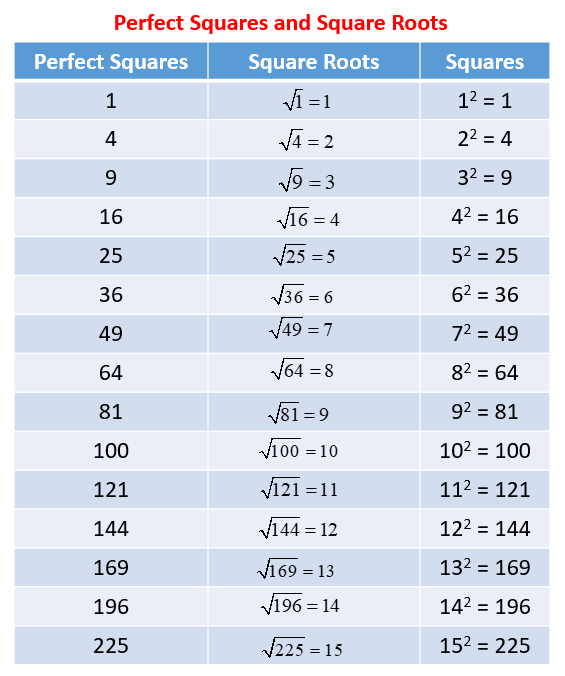
Introduction to Square Roots
The square root is a fundamental mathematical concept used to determine a number which, when multiplied by itself, gives the original number. It is denoted by the radical symbol . For example, the square root of 9 is 3, because 3 multiplied by 3 equals 9.
Key points about square roots include:
- Notation: The square root of a number x is written as .
- Positive and Negative Roots: Every positive number has two square roots: one positive and one negative. For example, the square roots of 16 are 4 and -4.
- Perfect Squares: Numbers like 1, 4, 9, 16, and 25 are perfect squares because they are squares of whole numbers.
- Irrational Numbers: Some square roots, like and , are irrational numbers and cannot be expressed as exact fractions or decimals.
To calculate the square root of a number, you can use several methods, including:
- Prime Factorization: Breaking down the number into its prime factors and pairing them to simplify the root.
- Estimation: Using nearby perfect squares to approximate the root.
- Long Division Method: A more precise manual method for finding square roots.
- Calculators: Electronic or online tools for quick and accurate square root calculations.
Understanding square roots is crucial for various mathematical applications, including solving quadratic equations, working with exponents and radicals, and in geometry for finding distances and areas.
Understanding the Expression 4 √6
When we encounter the expression 4 √6, we are essentially dealing with the square root of 6, multiplied by 4. Let's break this down:
- Square Root of 6: The square root of a number is a value that, when multiplied by itself, gives the original number. In this case, the square root of 6 is approximately 2.449.
- Multiplication by 4: Multiplying the square root of 6 by 4 simply means taking the value of the square root of 6 and multiplying it by 4. This results in 9.798 (approximately).
So, when we see 4 √6, we are essentially referring to a value around 9.798.
Calculating 4 √6
To calculate 4 times the square root of 6, we can follow these steps:
- Find the Square Root of 6: The square root of 6 is approximately 2.449.
- Multiply by 4: Multiply the square root of 6 by 4. This results in approximately 9.798.
So, 4 times the square root of 6 is around 9.798.
Approximation and Exact Values
When dealing with the expression 4 √6, it's important to understand both its approximation and exact values:
| Approximation: | As previously mentioned, the square root of 6 is approximately 2.449. Multiplying this by 4 yields an approximation of 9.798. |
| Exact Value: | The exact value of 4 √6 is an irrational number, meaning it cannot be expressed as a simple fraction. It is approximately 9.798, but this is only an approximation. |

Step-by-Step Calculation
Here's a step-by-step guide to calculate 4 times the square root of 6:
- Find the Square Root of 6: The square root of 6 is approximately 2.449.
- Multiply by 4: Multiply the square root of 6 by 4. This results in approximately 9.798.
So, 4 times the square root of 6 is around 9.798.
Mathematical Properties of √6
The square root of 6, denoted as √6, has several mathematical properties:
- Irreducibility: √6 is an irrational number, meaning it cannot be expressed as a simple fraction. It goes on infinitely without repeating.
- Approximation: While √6 is irrational, it can be approximated as approximately 2.449.
- Algebraic Property: In algebra, √6 can be used in various equations and expressions, particularly those involving radicals.
- Geometric Interpretation: √6 can represent the length of the diagonal of a square with side length 6 units.
- Trigonometric Applications: In trigonometry, √6 can be involved in calculations related to angles and side lengths in right triangles.
Applications in Algebra
The square root of 6, represented as √6, finds various applications in algebra:
- Radical Equations: √6 can be involved in solving radical equations where the variable is under a square root.
- Quadratic Equations: In quadratic equations, the square root of 6 may appear as part of the solution set.
- Complex Numbers: When dealing with complex numbers, expressions involving √6 may arise, especially in the context of finding roots of polynomials.
- Algebraic Manipulations: Manipulating expressions with √6 may be necessary when simplifying algebraic expressions or solving equations.
Applications in Geometry
The square root of 6, denoted as √6, has several applications in geometry:
- Diagonal Length: √6 can represent the length of the diagonal of a square with side length 6 units. This is useful in calculating distances or dimensions within geometric shapes.
- Area and Perimeter: In geometric problems involving squares or rectangles, √6 may be used to calculate the diagonal, which in turn can help find the area, perimeter, or other properties of the shape.
- Pythagorean Theorem: In right triangles where one side has a length of 6 units and the other side has a length of √6 units, the Pythagorean theorem can be applied to find the length of the hypotenuse.
- Geometric Constructions: √6 can be used as a measurement in geometric constructions, particularly when constructing shapes with specific ratios or proportions.
Applications in Trigonometry
The square root of 6, represented as √6, has several applications in trigonometry:
- Right Triangles: In right triangles where one of the acute angles is known, √6 can be used to find the length of a side opposite that angle using trigonometric ratios such as sine and cosine.
- Trigonometric Identities: √6 may appear in trigonometric identities and equations, especially when simplifying expressions or solving equations involving radicals.
- Graphs of Trigonometric Functions: The value of √6 can influence the shape and position of graphs of trigonometric functions, particularly sine and cosine functions.
- Angles of Elevation and Depression: In problems involving angles of elevation or depression, where the height or distance is given, √6 may be used in trigonometric calculations to find missing values.
Importance in Mathematical Context
The square root of 6, denoted as √6, holds significance in various mathematical contexts:
- Number Theory: √6 is an irrational number, providing insight into the properties of irrational numbers and their relationships with integers and rational numbers.
- Geometry: √6 is used in geometric calculations involving lengths, areas, and volumes, contributing to the understanding of geometric shapes and their properties.
- Algebra: In algebra, expressions containing √6 may arise in equations, inequalities, and polynomial functions, showcasing its role in algebraic manipulation and solution techniques.
- Trigonometry: √6 appears in trigonometric calculations, aiding in the analysis of angles, distances, and relationships between trigonometric functions.
- Real Analysis: The properties of √6 are explored in real analysis, providing insights into convergence, limits, and continuity of functions.
Real-World Examples
Understanding the practical applications of the expression \(4 \sqrt{6}\) helps in comprehending its significance in various real-world contexts. Below are some examples where square roots, including \(4 \sqrt{6}\), are essential:
-
Construction and Architecture:
In construction, square roots are frequently used to determine the lengths of sides in right triangles. For instance, the Pythagorean Theorem \(a^2 + b^2 = c^2\) can be solved using square roots to find the length of a diagonal support. If a structure needs a diagonal support where the other two sides are 6 feet and 8 feet, the length of the support can be found as follows:
\[
\sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10 \text{ feet}
\] -
Navigation and Mapping:
Square roots are used in navigation to calculate the distance between two points in a plane using the distance formula derived from the Pythagorean Theorem. For example, the distance \(D\) between points \((x_1, y_1)\) and \((x_2, y_2)\) is:
\[
D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]In three dimensions, this extends to:
\[
D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}
\] -
Physics and Engineering:
In physics, square roots are essential for solving equations related to motion and forces. For example, the quadratic formula, which includes a square root, is used to find the roots of quadratic equations in various physics problems. If an object is dropped from a height, its position over time can be modeled, and the square root can help find specific points in time. For instance, if an object is dropped from 400 feet, its height after \(t\) seconds is given by:
\[
h(t) = 400 - 16t^2
\]Solving for when the object reaches 144 feet involves:
\[
144 = 400 - 16t^2 \implies 16t^2 = 256 \implies t^2 = 16 \implies t = 4 \text{ seconds}
\] -
Graphic Design and Gaming:
In graphic design and gaming, the calculation of distances in 2D and 3D spaces is crucial. For instance, in a 2D space, the distance between two points is calculated using the distance formula:
\[
D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]In a 3D space, it extends to:
\[
D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}
\]These calculations are fundamental for creating realistic graphics and movement within a virtual environment.
-
Quality Control in Manufacturing:
Square roots are also used in quality control processes within manufacturing. By analyzing the distribution of product measurements, manufacturers can ensure consistency and quality. Products falling within a normal distribution range are considered acceptable, while those outside (calculated using square roots) are flagged for inspection.
These examples illustrate the versatility and importance of square roots in various fields, from construction and navigation to physics and graphic design.
Common Mistakes and Misconceptions
Understanding and working with the expression \(4\sqrt{6}\) can sometimes lead to common mistakes and misconceptions. Below are several key points to be aware of:
-
Misinterpreting the Radical Symbol: The square root symbol (√) represents the principal (positive) square root. A common mistake is to ignore the fact that squaring both positive and negative values can yield the same result. For instance, while \(\sqrt{36} = 6\), it is also true that \(\sqrt{36} = -6\). However, the square root function by convention only returns the positive root.
-
Incorrect Application of the Radical Rule: A frequent error is assuming that the square root of a sum or difference can be split into the sum or difference of the square roots. This is incorrect. For example:
\(\sqrt{x + y} \neq \sqrt{x} + \sqrt{y}\)
Instead, \(\sqrt{x + y}\) must be treated as a single entity unless simplified by specific algebraic identities or numerical values.
-
Confusing Radicals with Other Operations: Another common error is treating radicals similarly to exponents or coefficients. For example:
\(\sqrt{x \cdot y} = \sqrt{x} \cdot \sqrt{y}\) is only valid when both x and y are non-negative. Be cautious with negative numbers and remember that \(\sqrt{x \cdot y} \neq \sqrt{x} \cdot \sqrt{y}\) if x or y is negative.
-
Ignoring Order of Operations: When performing calculations involving radicals, it is crucial to adhere to the proper order of operations (PEMDAS/BODMAS). For instance:
Calculate the radical first before multiplying by any coefficients. For example, in \(4\sqrt{6}\), first find \(\sqrt{6}\) and then multiply by 4.
-
Assuming All Radicals Simplify Neatly: Not all square roots will simplify to neat integers or simple fractions. For example:
\(\sqrt{6}\) does not simplify neatly. Instead, it is an irrational number approximately equal to 2.449.
-
Mistakes in Simplifying Expressions: Simplifying expressions involving radicals can be tricky. For instance, consider:
\(4\sqrt{6} \neq \sqrt{24}\)
Instead, recognize that \(4\sqrt{6}\) should be treated as \(4 \times \sqrt{6}\).
-
Common Algebraic Errors: These include errors in distributing coefficients, combining terms incorrectly, or mishandling radical expressions in equations. Always follow algebraic rules carefully and check work for these common pitfalls.
By understanding and avoiding these common mistakes and misconceptions, you can more accurately work with expressions involving square roots and ensure correct solutions in your mathematical calculations.

Practice Problems and Solutions
Here are several practice problems to help you master the concept of calculating \( 4\sqrt{6} \). These problems will cover various scenarios to deepen your understanding.
-
Problem 1: Simplify \( 4 \sqrt{6} \times 2 \sqrt{6} \).
Solution:
First, multiply the coefficients and the square roots separately:
\[
4 \sqrt{6} \times 2 \sqrt{6} = (4 \times 2) \times (\sqrt{6} \times \sqrt{6}) = 8 \times 6 = 48
\]Thus, \( 4 \sqrt{6} \times 2 \sqrt{6} = 48 \).
-
Problem 2: Simplify \( \frac{12 \sqrt{6}}{3 \sqrt{2}} \).
Solution:
Divide the coefficients and the square roots separately:
\[
\frac{12 \sqrt{6}}{3 \sqrt{2}} = \frac{12}{3} \times \frac{\sqrt{6}}{\sqrt{2}} = 4 \times \sqrt{\frac{6}{2}} = 4 \times \sqrt{3}
\]Thus, \( \frac{12 \sqrt{6}}{3 \sqrt{2}} = 4 \sqrt{3} \).
-
Problem 3: Solve for \( x \) in the equation \( 2x^2 = 8 \sqrt{6} \).
Solution:
First, isolate \( x^2 \) by dividing both sides by 2:
\[
x^2 = \frac{8 \sqrt{6}}{2} = 4 \sqrt{6}
\]Next, take the square root of both sides:
\[
x = \pm \sqrt{4 \sqrt{6}} = \pm 2 \sqrt[4]{6}
\]Thus, \( x = 2 \sqrt[4]{6} \) or \( x = -2 \sqrt[4]{6} \).
-
Problem 4: Evaluate \( (4 \sqrt{6})^2 \).
Solution:
Square the coefficient and the square root separately:
\[
(4 \sqrt{6})^2 = 4^2 \times (\sqrt{6})^2 = 16 \times 6 = 96
\]Thus, \( (4 \sqrt{6})^2 = 96 \).
-
Problem 5: Simplify \( 5 \sqrt{24} - 2 \sqrt{54} \).
Solution:
First, simplify the square roots:
\[
5 \sqrt{24} = 5 \sqrt{4 \times 6} = 5 \times 2 \sqrt{6} = 10 \sqrt{6}
\]\[
2 \sqrt{54} = 2 \sqrt{9 \times 6} = 2 \times 3 \sqrt{6} = 6 \sqrt{6}
\]Then subtract the simplified terms:
\[
10 \sqrt{6} - 6 \sqrt{6} = 4 \sqrt{6}
\]Thus, \( 5 \sqrt{24} - 2 \sqrt{54} = 4 \sqrt{6} \).
These problems should help reinforce your understanding of operations involving \( 4 \sqrt{6} \). Practice these problems to become more comfortable with the calculations.
Advanced Topics Related to Square Roots
In this section, we will explore advanced topics related to square roots, including their properties, theorems, and applications in higher mathematics. Understanding these concepts can provide a deeper insight into the mathematical significance and utility of square roots.
1. Properties of Square Roots
- Rationalizing the Denominator: The process of removing a square root from the denominator of a fraction by multiplying both the numerator and the denominator by an appropriate value.
- Irrational Numbers: Square roots of non-perfect squares are irrational, meaning they cannot be expressed as a ratio of two integers.
- Simplifying Square Roots: Breaking down the radicand into its prime factors to simplify the square root expression.
2. Theorems Involving Square Roots
- Square Root Function: The function \( f(x) = \sqrt{x} \) is defined for \( x \geq 0 \) and is a one-to-one function.
- Pythagorean Theorem: In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides, often involving square roots in its calculations.
- Quadratic Formula: The solutions to the quadratic equation \( ax^2 + bx + c = 0 \) are given by \( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \), involving the square root of the discriminant.
3. Applications in Higher Mathematics
Square roots are used extensively in various branches of higher mathematics, including algebra, calculus, and complex analysis.
- Complex Numbers: The square root of a negative number introduces imaginary numbers, defined as \( i = \sqrt{-1} \), leading to the complex plane and complex analysis.
- Eigenvalues and Eigenvectors: In linear algebra, square roots appear in the characteristic equation used to find eigenvalues of a matrix.
- Calculus: Square roots are involved in differentiation and integration, especially in problems involving distance and area calculations.
4. Advanced Techniques
- Conjugate Pairs: Utilizing the property of conjugates to simplify expressions involving square roots, particularly in complex number calculations.
- Nested Radicals: Expressions containing multiple layers of square roots, which can sometimes be simplified using algebraic identities.
- Infinite Series: Representing square roots as infinite series, such as through the binomial series expansion.
5. Special Functions Involving Square Roots
- Gamma Function: Extends the factorial function to complex numbers, often involving square roots in its properties and calculations.
- Elliptic Integrals: Integrals involving square roots that arise in the calculation of arc lengths of ellipses and other applications in physics and engineering.
- Legendre Polynomials: Solutions to Legendre's differential equation, used in physics and engineering, often involve square roots in their formulation.
By delving into these advanced topics, one can appreciate the profound impact and utility of square roots across various fields of mathematics and science.
Conclusion
The exploration of the expression \(4 \sqrt{6}\) reveals its multifaceted nature in mathematical contexts. This value, approximately equal to 9.79796, highlights the importance of understanding square roots and their applications across various fields of study.
Square roots play a crucial role in algebra, geometry, and trigonometry, providing foundational tools for solving equations, calculating distances, and understanding the properties of shapes and angles. The square root of 6, specifically, is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal representation is non-terminating and non-repeating.
In advanced mathematics, square roots like \( \sqrt{6} \) are involved in various complex calculations and theories. For example, they appear in the solutions of quadratic equations, the simplification of radical expressions, and the computation of areas and volumes in higher dimensions.
Real-world applications of \(4 \sqrt{6}\) extend to physics, engineering, and computer science, where precise calculations are necessary. Understanding and accurately computing square roots ensure better problem-solving and analytical capabilities in these fields.
To further enhance your grasp on square roots and their applications, practice problems, and real-life examples are invaluable. These not only solidify theoretical knowledge but also improve practical skills in handling complex mathematical tasks.
In summary, \(4 \sqrt{6}\) exemplifies the elegance and utility of square roots in mathematics. Whether dealing with basic computations or advanced mathematical concepts, mastering the properties and applications of square roots is essential for mathematical proficiency and success.
Khám phá cách tính căn bậc hai của 6 với ví dụ minh họa và giải thích chi tiết. Học cách áp dụng trong các bài toán thực tế.
Căn Bậc Hai của 6
READ MORE:
Video hướng dẫn cách đơn giản hóa căn bậc hai một cách dễ hiểu và chi tiết, giúp người học dễ dàng nắm bắt.
Cách Đơn Giản Hóa Căn Bậc Hai