Topic square root 72: The square root of 72 is an intriguing mathematical concept that can be expressed in both exact and decimal forms. In this article, we will explore various methods to calculate and simplify √72, its properties, and practical applications. Whether you're a student or a math enthusiast, understanding the square root of 72 will enhance your mathematical knowledge.
Table of Content
- Square Root of 72
- Introduction to Square Root of 72
- Exact Form and Decimal Approximation
- Prime Factorization Method
- Long Division Method
- Simplification of √72
- Radical Form
- Nearest Tenth and Hundredth
- Rational or Irrational Nature
- Applications in Mathematics
- Geometry and Algebra
- Real-World Problems
- Examples and Problems
- Proving 72 is Not a Perfect Square
- Finding Side Length of a Square
- FAQs on Square Root of 72
- Can the Square Root of 72 be Simplified?
- What is the Square Root of 72 Rounded to its Nearest Tenth?
- Is the Square Root of 72 a Real Number?
- YOUTUBE: Hướng dẫn tính căn bậc hai của 72 (√72) một cách chi tiết và dễ hiểu. Phù hợp cho những ai muốn nắm vững kiến thức toán học cơ bản.
Square Root of 72
The square root of 72 is a mathematical value that, when multiplied by itself, equals 72. It is often represented as √72 and can be expressed in different forms.
Exact Form
The exact form of the square root of 72 is:
√72 = 6√2
Decimal Form
The decimal approximation of the square root of 72 is:
√72 ≈ 8.48528137423857
Methods to Calculate the Square Root of 72
- Prime Factorization Method: By factoring 72 into its prime factors and grouping them, we get:
- Prime factorization: \( 72 = 2^3 \times 3^2 \)
- Grouping into pairs: \( 72 = (2 \times 2) \times 2 \times (3 \times 3) \)
- Taking the square root of the groups: \( \sqrt{72} = \sqrt{(2 \times 2) \times 2 \times (3 \times 3)} = 6\sqrt{2} \)
- Long Division Method: Using the long division method, we can approximate the square root of 72 step-by-step to get a more precise decimal value.
Properties of the Square Root of 72
| Property | Value |
| Radical Form | 6√2 |
| Decimal Form (approx.) | 8.48528137423857 |
| Nearest Tenth | 8.5 |
| Nearest Hundredth | 8.49 |
| Rational or Irrational | Irrational |
Applications
The square root of 72 is used in various mathematical problems, including geometry, algebra, and calculus. It can be applied in real-world situations such as calculating areas and solving quadratic equations.
Examples
- Example 1: Proving 72 is not a perfect square.
Since the square root of 72 is not an integer, 72 is not a perfect square.
- Example 2: Finding the side length of a square with an area of 72.
If the area of a square is 72, then the side length is \( \sqrt{72} \approx 8.49 \).

READ MORE:
Introduction to Square Root of 72
The square root of 72 is a value that, when multiplied by itself, gives the number 72. It is an important concept in mathematics, especially in the context of algebra and geometry. The square root of a number is one of its two equal factors. For instance, the square root of 72 can be expressed using the radical symbol as √72.
Understanding the square root of 72 involves breaking down the number into its prime factors and simplifying it to its exact form, as well as approximating it to a decimal form for practical use. Here, we will explore both the exact form and the decimal approximation, along with methods to calculate and simplify the square root of 72.
The number 72 is not a perfect square, meaning its square root is not an integer. Instead, the square root of 72 is an irrational number, which cannot be expressed as a simple fraction and has an infinite, non-repeating decimal expansion. Despite this, it can be approximated to a reasonable degree of accuracy for practical purposes.
In summary, the square root of 72 is an intriguing mathematical concept with various applications in different fields. Whether you are solving algebraic equations, working on geometric problems, or dealing with real-world scenarios, understanding the square root of 72 is essential. Let us delve deeper into its exact form, methods of calculation, properties, and applications in the sections that follow.
Exact Form and Decimal Approximation
The square root of 72 can be expressed in different forms, providing both exact and approximate values.
Exact Form
- Radical Form: \( \sqrt{72} \)
- Simplified Radical Form: \( 6\sqrt{2} \)
- Exponential Form: \( (72)^{1/2} \)
Decimal Approximation
When the square root of 72 is calculated, its decimal form is approximately:
- Decimal Form: \( \approx 8.48528137423857 \)
This approximation can be further rounded for simplicity:
- To the Nearest Tenth: \( \approx 8.5 \)
- To the Nearest Hundredth: \( \approx 8.49 \)
The exact form \( 6\sqrt{2} \) is often used in mathematical calculations for precision, while the decimal approximation is useful for practical applications and easier interpretation.
Prime Factorization Method
The prime factorization method is an effective way to find the square root of a number by breaking it down into its prime factors and then simplifying the square root expression. Here's how you can use this method to find the square root of 72:
- First, find the prime factors of 72.
- 72 can be divided by 2, which is the smallest prime number.
- \(72 \div 2 = 36\)
- Continue dividing by 2: \(36 \div 2 = 18\)
- Again, divide by 2: \(18 \div 2 = 9\)
- Now, 9 is not divisible by 2, so we move to the next smallest prime number, which is 3: \(9 \div 3 = 3\)
- Finally, divide by 3: \(3 \div 3 = 1\)
- Next, pair the prime factors.
- Simplify the square root using the pairs.
- Each pair of prime factors can be taken out of the square root as a single factor.
- \(\sqrt{72} = \sqrt{(2^2 \times 3^2) \times 2}\)
- \(\sqrt{72} = 2 \times 3 \times \sqrt{2}\)
- \(\sqrt{72} = 6\sqrt{2}\)
Thus, the prime factorization of 72 is \(2 \times 2 \times 2 \times 3 \times 3\) or \(2^3 \times 3^2\).
We can pair the factors as follows: \((2 \times 2) \times (3 \times 3) \times 2\).
Therefore, the exact form of the square root of 72 using prime factorization is \(6\sqrt{2}\). This method provides a simplified radical form of the square root, making it easier to understand and use in further calculations.
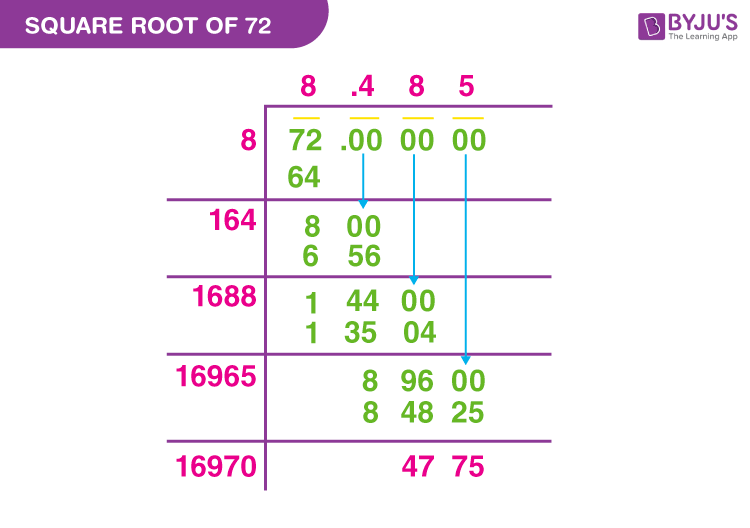
Long Division Method
The Long Division Method is a systematic approach to find the square root of a number. Below are the detailed steps to calculate the square root of 72 using this method:
Write the number 72.000000 under the long division symbol. Since 72 is not a perfect square, we add pairs of zeros after the decimal point for accuracy.
Starting from the left, find the largest number whose square is less than or equal to 72. In this case, it is 8 because \(8^2 = 64\) and \(9^2 = 81\) which is more than 72.
Write 8 as the first digit of the quotient. Subtract 64 (which is \(8^2\)) from 72, giving a remainder of 8.
Bring down the next pair of zeros. Now, the new number is 800. Double the quotient (8) to get 16 and place it next to 8.
Find a number (X) such that 16X multiplied by X is less than or equal to 800. The number is 4 because \(164 \times 4 = 656\). Write 4 in the quotient and also as part of the new divisor.
Subtract 656 from 800 to get 144. Bring down the next pair of zeros, making it 14400.
Double the quotient (84) to get 168 and place it next to 14400.
Find a number (X) such that 168X multiplied by X is less than or equal to 14400. The number is 8 because \(1688 \times 8 = 13504\). Write 8 in the quotient and also as part of the new divisor.
Subtract 13504 from 14400 to get 896. Bring down the next pair of zeros, making it 89600.
Double the quotient (848) to get 1696 and place it next to 89600.
Find a number (X) such that 1696X multiplied by X is less than or equal to 89600. The number is 5 because \(16965 \times 5 = 84825\). Write 5 in the quotient and also as part of the new divisor.
Subtract 84825 from 89600 to get 4775. Bring down the next pair of zeros, making it 477500.
Continue this process until you reach the desired accuracy. The square root of 72 is approximately 8.48528137423857.
This method provides a precise way to find the square root of 72, yielding the value as 8.485 when rounded to three decimal places.
Simplification of √72
The simplification of the square root of 72 involves expressing the radical in its simplest form. This process can be broken down into the following steps:
- Find the Prime Factors of 72:
- 72 can be factored into prime numbers as: 72 = 2 × 2 × 2 × 3 × 3
- Pair the Prime Factors:
- Group the factors into pairs of identical numbers: 72 = (2 × 2) × (3 × 3) × 2
- Simplify the Radical:
- According to the properties of square roots, √(a × b) = √a × √b.
- Thus, √72 can be simplified as √[(2 × 2) × (3 × 3) × 2] = √(2²) × √(3²) × √2 = 2 × 3 × √2.
- Combine the simplified parts: 2 × 3 × √2 = 6√2.
Therefore, the simplest form of √72 is:
√72 = 6√2
This means that the square root of 72 in its simplest radical form is 6 times the square root of 2.
Here is a step-by-step table summarizing the simplification process:
| Step | Action | Result |
|---|---|---|
| 1 | Factorize 72 into primes | 72 = 2 × 2 × 2 × 3 × 3 |
| 2 | Group pairs of primes | (2 × 2) × (3 × 3) × 2 |
| 3 | Apply square root properties | √(2²) × √(3²) × √2 |
| 4 | Simplify | 2 × 3 × √2 = 6√2 |
By following these steps, you can simplify the square root of 72 to its simplest form, 6√2.
Radical Form
The square root of 72 can be expressed in its simplest radical form by breaking down the number into its prime factors.
- Step 1: Find the prime factors of 72.
- Step 2: Group the prime factors into pairs.
- Step 3: Simplify the square root of the grouped factors.
\[
72 = 2^3 \times 3^2
\]
\[
72 = (2^2 \times 3^2) \times 2 = 36 \times 2
\]
\[
\sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2}
\]
Therefore, the radical form of the square root of 72 is \(6\sqrt{2}\).
This simplified form is useful in various mathematical computations, as it represents the exact form of the square root without any decimal approximation.
Nearest Tenth and Hundredth
To the nearest tenth, \( \sqrt{72} \approx 8.5 \).
To the nearest hundredth, \( \sqrt{72} \approx 8.49 \).
Rational or Irrational Nature
The square root of 72 is an irrational number. This means it cannot be expressed as a simple fraction (i.e., a ratio of two integers). The decimal representation of \( \sqrt{72} \) is non-terminating and non-repeating.

Applications in Mathematics
The square root of 72 has various applications across different branches of mathematics:
- Geometry: In geometry, the square root of 72 is used to calculate the side length of a square whose area is 72 square units.
- Algebra: In algebra, it appears in solving quadratic equations and in simplifying expressions involving radicals.
- Number Theory: It contributes to discussions about perfect squares and non-perfect squares, as 72 is not a perfect square.
- Approximations: The square root of 72 is often approximated for practical calculations where precise values are not necessary.
- Mathematical Problems: It serves as a topic for various problem-solving exercises, challenging students' understanding of square roots and their properties.
- Mathematical Modeling: In real-world applications, such as physics and engineering, understanding the square root of 72 can aid in modeling scenarios where square roots naturally occur.
Geometry and Algebra
The square root of 72 (\(\sqrt{72}\)) has interesting applications in both geometry and algebra. Let's explore some key concepts and examples.
Geometry
In geometry, the square root of 72 is often used to find lengths and distances. For instance, consider a square with an area of 72 square units. The side length of this square can be found by taking the square root of the area:
\[ \text{Side length} = \sqrt{72} = 6\sqrt{2} \approx 8.49 \text{ units} \]
This means each side of the square measures approximately 8.49 units.
Another geometric application involves circles. If a circle has an area of \(72\pi\) square units, its radius \(r\) can be found as follows:
\[ \pi r^2 = 72\pi \implies r^2 = 72 \implies r = \sqrt{72} = 6\sqrt{2} \approx 8.49 \text{ units} \]
Algebra
In algebra, \(\sqrt{72}\) is used to simplify expressions and solve equations. For example, simplifying the radical expression \(\sqrt{72}\) involves finding its prime factorization:
\[ 72 = 2 \times 2 \times 2 \times 3 \times 3 = 2^3 \times 3^2 \]
Thus, the simplified radical form is:
\[ \sqrt{72} = \sqrt{2^3 \times 3^2} = \sqrt{(2^2 \times 3^2) \times 2} = 6\sqrt{2} \]
This shows that \(\sqrt{72}\) can be expressed as \(6\sqrt{2}\), which is useful in various algebraic operations.
Example Problem
Let's consider an example problem to illustrate the use of \(\sqrt{72}\) in algebra:
- Find the length of the diagonal of a rectangle with sides 6 units and 12 units.
The length of the diagonal \(d\) can be found using the Pythagorean theorem:
\[ d = \sqrt{6^2 + 12^2} = \sqrt{36 + 144} = \sqrt{180} = \sqrt{36 \times 5} = 6\sqrt{5} \]
To further simplify, note that \( \sqrt{180} \) is closer to \( \sqrt{169} \) and \( \sqrt{196} \), giving us an approximation.
In summary, \(\sqrt{72}\) is an important value in both geometry and algebra, providing solutions to problems involving areas, lengths, and algebraic simplifications.
Real-World Problems
The square root of 72 finds application in various real-world scenarios. Here are a few examples:
-
Construction and Architecture:
In building construction, square roots are essential for determining diagonal lengths. For instance, when creating diagonal braces for a rectangular frame, you can use the square root to find the precise length needed for structural integrity. If a wall is 72 square units, you can find the length of its diagonal by calculating the square root of 72.
-
Geometry and Design:
Square roots are crucial in geometric calculations, such as finding the side length of a square with a given area. For example, if a square has an area of 72 square units, the length of each side is the square root of 72, which is approximately 8.49 units. This calculation helps in designing square-shaped gardens, tiles, or plots.
-
Science and Engineering:
In physics, square roots are used to determine quantities like speed and distance. For instance, if an object's motion equation involves the square root of a number, calculating the square root of 72 can help find the distance it travels over a specific period.
-
Finance:
In finance, square roots are used to calculate volatility. The standard deviation, which measures the volatility of an investment, involves taking the square root of the variance. If the variance of a stock's returns is 72, the standard deviation would be the square root of 72, indicating the investment's risk level.
-
Navigation:
In navigation, square roots help calculate distances. For example, the Pythagorean theorem, which involves square roots, can determine the shortest path between two points. If the coordinates of a route require the square root of 72, this value aids in plotting the accurate distance on a map.
Understanding the square root of 72 and its applications enhances problem-solving skills in various fields, from construction to finance, demonstrating its importance in practical scenarios.
Examples and Problems
Here are some examples and problems related to the square root of 72:
- Example 1: Calculate \( \sqrt{72} \) to the nearest tenth.
- Problem 1: Find the square root of 72 using the long division method.
- Example 2: Simplify \( \sqrt{72} \) in radical form.
- Problem 2: Determine whether \( \sqrt{72} \) is a rational or irrational number.
- Example 3: Use the prime factorization method to find \( \sqrt{72} \).
- Problem 3: Find the side length of a square with an area of 72 square units.

Proving 72 is Not a Perfect Square
To prove that 72 is not a perfect square, we can follow these steps:
- Step 1: Recognize that a perfect square is a number that can be expressed as \( n^2 \), where \( n \) is an integer.
- Step 2: Calculate the square root of 72, \( \sqrt{72} \).
- Step 3: Determine whether \( \sqrt{72} \) is an integer or not.
- Step 4: If \( \sqrt{72} \) is not an integer, then 72 is not a perfect square.
- Step 5: Verify that \( \sqrt{72} \) is not equal to any integer by using approximation or exact calculation methods.
Finding Side Length of a Square
To find the side length \( s \) of a square with an area of 72 square units, follow these steps:
- Step 1: Recall the formula for the area of a square: \( \text{Area} = s^2 \).
- Step 2: Set up the equation using the given area: \( s^2 = 72 \).
- Step 3: Solve for \( s \) by taking the square root of both sides: \( s = \sqrt{72} \).
- Step 4: Calculate \( \sqrt{72} \) either in decimal form or simplify it in radical form.
- Step 5: Therefore, the side length \( s \) of the square with an area of 72 square units is \( \sqrt{72} \).
FAQs on Square Root of 72
-
Can the Square Root of 72 be Simplified?
Yes, the square root of 72 can be simplified. It simplifies to \( 6\sqrt{2} \) in radical form.
-
What is the Square Root of 72 Rounded to its Nearest Tenth?
The square root of 72 rounded to the nearest tenth is approximately 8.5.
-
Is the Square Root of 72 a Real Number?
Yes, the square root of 72 is a real number. It is approximately 8.48528137423857.
Can the Square Root of 72 be Simplified?
Yes, the square root of 72 can be simplified. It simplifies to \( 6\sqrt{2} \) in radical form.

What is the Square Root of 72 Rounded to its Nearest Tenth?
The square root of 72 is an important value in mathematics and can be found using various methods. When rounded to its nearest tenth, the square root of 72 provides a more convenient and approximate value for practical uses. Here, we will discuss how to find the square root of 72 and round it to its nearest tenth.
First, let's find the approximate value of the square root of 72:
\[
\sqrt{72} \approx 8.48528137423857
\]
To round this to the nearest tenth, we look at the digit in the hundredths place (the second digit after the decimal point). In this case, the digit is 4.
Since the hundredths place digit is less than 5, we round down:
\[
8.48528137423857 \approx 8.5
\]
Therefore, the square root of 72 rounded to its nearest tenth is:
\[
\boxed{8.5}
\]
Is the Square Root of 72 a Real Number?
The square root of 72 is indeed a real number. To understand why, let's delve into the definitions and properties of real numbers.
Real numbers include all the numbers that can be found on the number line. This includes both rational and irrational numbers. Rational numbers are numbers that can be expressed as the quotient of two integers, whereas irrational numbers cannot be expressed as a simple fraction and have non-repeating, non-terminating decimal expansions.
The square root of 72, denoted as √72, is approximately 8.48528137423857. This value cannot be expressed as a simple fraction, making it an irrational number. Despite being irrational, it is still classified as a real number.
Here are some key points about the square root of 72:
- Approximate Value: √72 ≈ 8.48528137423857
- Radical Form: √72
- Decimal Form: 8.48528137423857...
- Nature: Irrational number
Since irrational numbers are a subset of real numbers, we can confidently state that the square root of 72 is a real number.
In summary, √72 is real because it exists on the number line and can be approximated by a decimal that neither terminates nor repeats. This characteristic confirms its place within the set of real numbers.
Hướng dẫn tính căn bậc hai của 72 (√72) một cách chi tiết và dễ hiểu. Phù hợp cho những ai muốn nắm vững kiến thức toán học cơ bản.
Cách Tính Căn Bậc Hai của 72: Sqrt(72)
READ MORE:
Hướng dẫn cách đơn giản hóa căn bậc hai của một số, đặc biệt là căn bậc hai của 72 (√72). Video này sẽ giúp bạn hiểu rõ hơn về phương pháp đơn giản hóa số học.
Cách Tốt Nhất Để Đơn Giản Hóa Căn Bậc Hai của Một Số, Sqrt(72)








