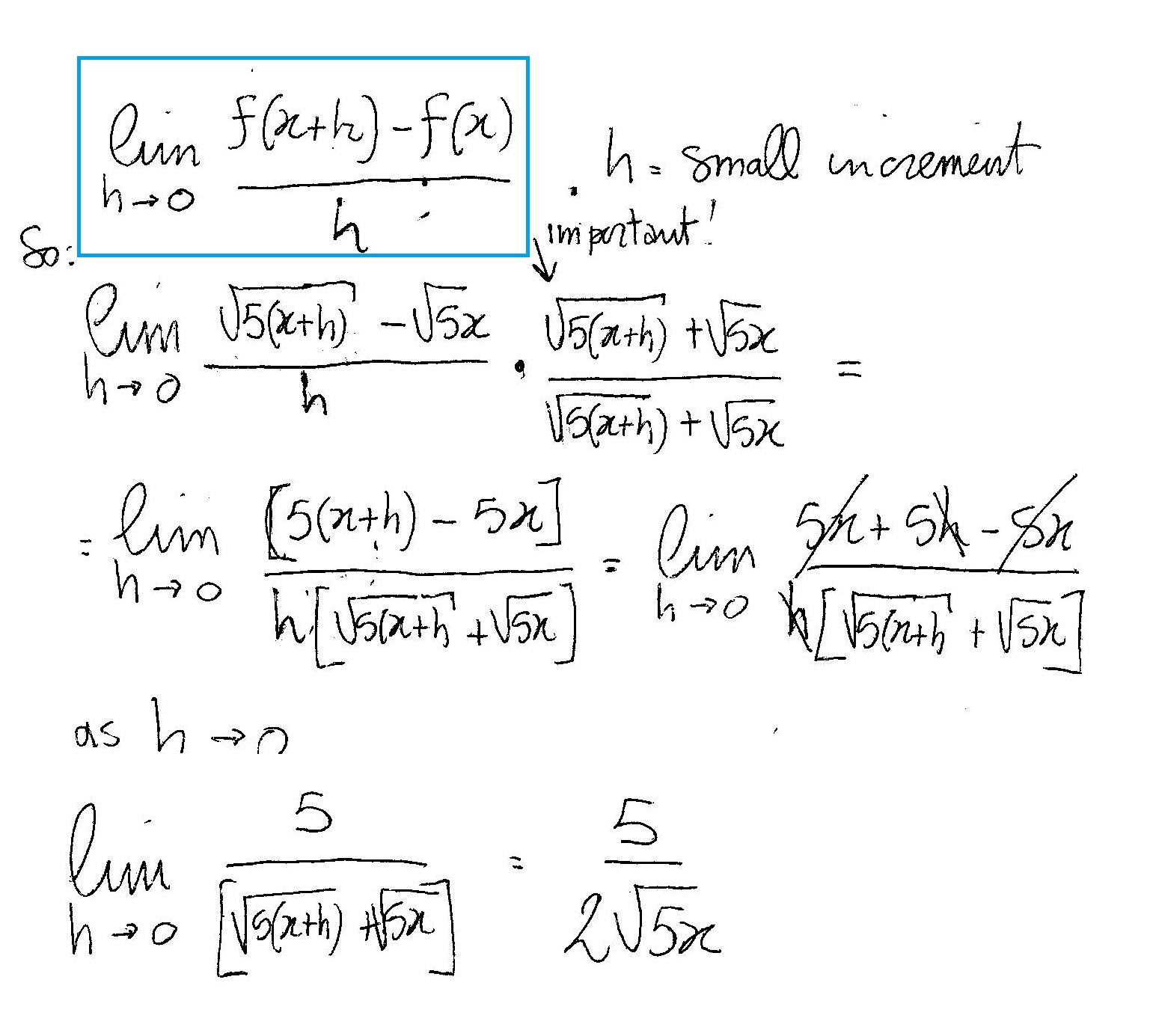
Topic square root 0f 5: The square root of 5 is a fascinating mathematical concept with wide-ranging applications in various fields. In this article, we will explore its properties, calculation methods, and significance in geometry, algebra, and beyond. Whether you're a student or a math enthusiast, this guide will deepen your understanding of the square root of 5.
Table of Content
- Square Root of 5
- Introduction to Square Roots
- Understanding the Square Root of 5
- Mathematical Representation of Square Root of 5
- Calculating the Square Root of 5
- Square Root of 5 in Decimal Form
- Applications of the Square Root of 5
- Square Root of 5 in Geometry
- Square Root of 5 in Algebra
- Historical Context of the Square Root of 5
- Square Root of 5 in Modern Mathematics
- Common Misconceptions about the Square Root of 5
- Square Root of 5 in Technology and Engineering
- Visualizing the Square Root of 5
- Advanced Topics Related to the Square Root of 5
- Conclusion: Importance of Understanding the Square Root of 5
- YOUTUBE: Video này giải thích cách đơn giản hóa căn bậc hai của 5, cung cấp hướng dẫn chi tiết và dễ hiểu cho người xem.
Square Root of 5
The square root of 5 is an important mathematical constant that appears in various mathematical contexts, including algebra, geometry, and number theory. It is an irrational number, which means it cannot be expressed as a simple fraction and has an infinite number of decimals without repeating.
Value of the Square Root of 5
The value of the square root of 5, rounded to 10 decimal places, is approximately:
\(\sqrt{5} \approx 2.2360679775\)
How to Find the Square Root of 5
There are several methods to find the square root of 5, including the long division method and using a calculator.
Long Division Method
- Estimate a number close to \(\sqrt{5}\).
- Divide 5 by this estimate.
- Average the result with the estimate.
- Repeat steps 2 and 3 until the desired accuracy is achieved.
Example
Using the long division method, the steps to approximate \(\sqrt{5}\) are as follows:
1. Initial estimate: 2.2
2. Divide: \(5 / 2.2 \approx 2.273\)
3. Average: \((2.2 + 2.273) / 2 \approx 2.2365\)
4. Repeat as necessary for more precision.
Properties of the Square Root of 5
- \(\sqrt{5}\) is an irrational number.
- In radical form, it is expressed as \(\sqrt{5}\).
- In exponent form, it is written as \(5^{1/2}\).
Geometric Interpretation
Geometrically, \(\sqrt{5}\) can be seen as the diagonal of a rectangle with sides 1 and 2, using the Pythagorean theorem.
\[
\sqrt{5} = \sqrt{1^2 + 2^2} = \sqrt{1 + 4} = \sqrt{5}
\]
Applications in Mathematics
The square root of 5 appears in various mathematical problems and contexts, such as the diagonal of a 1x2 rectangle and the solution to quadratic equations.
Related Formulas
- The area of a square with side length \(\sqrt{5}\) is 5.
- The square root of a product: \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\).
- The square root of a fraction: \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\).
FAQs on the Square Root of 5
- What is the square root of 5 in simplest radical form? The simplest radical form is \(\sqrt{5}\).
- Why is the square root of 5 irrational? Because it cannot be expressed as a fraction of two integers.
- What is the square root of -5? The square root of -5 is an imaginary number: \(\sqrt{-5} = i\sqrt{5}\).

READ MORE:
Introduction to Square Roots
Square roots are a fundamental concept in mathematics, particularly in algebra and geometry. They are the inverse operation of squaring a number. For a non-negative real number \( x \), the square root of \( x \), denoted as \( \sqrt{x} \), is the value \( y \) such that \( y \geq 0 \) and \( y^2 = x \).
The concept of square roots extends beyond basic arithmetic into more advanced mathematical fields, including calculus, where it plays a crucial role in functions and equations involving roots.
- Square roots are used extensively in various practical applications, such as physics, engineering, and computer science.
- They are essential in geometry for calculating side lengths of right triangles and in algebra for solving quadratic equations.
- Understanding square roots is foundational for comprehending complex numbers and their operations.
Throughout history, mathematicians have developed methods for approximating square roots and understanding their properties, leading to their widespread use in both theoretical and practical contexts.
Understanding the Square Root of 5
The square root of 5, represented as \( \sqrt{5} \), is an irrational number, meaning it cannot be expressed as a simple fraction and has an infinite number of non-repeating decimals. Its approximate value is 2.23606797749979.
Mathematically, \( \sqrt{5} \) is defined as the number that, when multiplied by itself, equals 5. This is known as the principal square root, distinguishing it from the negative counterpart \(-\sqrt{5}\).
Properties of \( \sqrt{5} \)
- It is an irrational number.
- It has an infinite decimal expansion without a repeating pattern.
- It appears in various mathematical contexts, including algebra and geometry.
Geometric Interpretation
Geometrically, \( \sqrt{5} \) can be understood as the length of the diagonal of a rectangle with sides of length 1 and 2, according to the Pythagorean theorem:
\[
\sqrt{1^2 + 2^2} = \sqrt{1 + 4} = \sqrt{5}
\]
Relationship to the Golden Ratio
The square root of 5 is closely related to the golden ratio \( \varphi \). The golden ratio is defined as \(\varphi = \frac{1 + \sqrt{5}}{2}\), which approximately equals 1.618. This relationship is fundamental in various fields of mathematics, particularly in the context of Fibonacci numbers and golden rectangles.
Calculating \( \sqrt{5} \)
The value of \( \sqrt{5} \) can be approximated using methods such as the division method. Here's a simplified version of the division method to find \( \sqrt{5} \):
- Estimate a number close to \( \sqrt{5} \). For example, between 2 and 3.
- Divide 5 by this estimate.
- Take the average of the estimate and the result from step 2.
- Use this average as the new estimate and repeat steps 2 and 3 until you reach a satisfactory level of accuracy.
This method will converge to a more precise value of \( \sqrt{5} \) with each iteration.
Applications of \( \sqrt{5} \)
\( \sqrt{5} \) appears in various applications, including:
- Calculations involving the golden ratio.
- Trigonometric identities and exact values for specific angles.
- Geometric constructions, such as root rectangles.
Understanding the square root of 5 provides insights into its role in mathematics and its applications in different fields.
Mathematical Representation of Square Root of 5
The square root of 5, denoted as \( \sqrt{5} \), is an irrational number, which means it cannot be expressed as a simple fraction. Its approximate decimal form is 2.23606797749979. Mathematically, it can be represented and understood in several ways:
- Radical Form: The most common representation is using the radical symbol: \( \sqrt{5} \).
- Exponential Form: It can also be written using exponents: \( 5^{\frac{1}{2}} \).
- Decimal Form: The square root of 5 is approximately 2.236068.
To express this value in a more detailed form:
\[
\sqrt{5} \approx 2.23606797749979
\]
This value continues infinitely without repeating, reflecting its irrational nature.
For a better understanding, we can use a table to see its value up to several decimal places:
| Decimal Place | Value |
|---|---|
| 1 | 2.2 |
| 2 | 2.23 |
| 3 | 2.236 |
| 4 | 2.2360 |
| 5 | 2.23607 |
| 6 | 2.236068 |
Another interesting way to represent \( \sqrt{5} \) is through its relationship with the golden ratio, \( \phi \). The golden ratio can be defined using \( \sqrt{5} \) as:
\[
\phi = \frac{1 + \sqrt{5}}{2} \approx 1.61803398874989
\]
This relationship highlights the importance of \( \sqrt{5} \) in various mathematical contexts, including geometry and algebra.
In algebra, we often encounter equations involving \( \sqrt{5} \). For instance, solving \( x^2 = 5 \) gives us the solutions \( x = \sqrt{5} \) and \( x = -\sqrt{5} \), demonstrating the principal square root and its negative counterpart.
Understanding the mathematical representation of \( \sqrt{5} \) helps in various fields such as geometry, where it is used to calculate lengths in right-angled triangles, and in algebra, for solving quadratic equations. Its irrational nature also makes it a subject of interest in number theory and real analysis.
Calculating the Square Root of 5
The square root of 5 can be calculated using various methods. Here, we will explore the long division method, which is effective for finding square roots of non-perfect squares.
Steps to Calculate the Square Root of 5 Using Long Division Method
- Write the number 5 as 5.00000000 to consider decimal places.
- Find the largest integer whose square is less than or equal to 5. In this case, 22 = 4.
- Divide 5 by 2, giving a quotient of 2. Write this quotient as the first part of the answer.
- Subtract 4 (22) from 5, leaving a remainder of 1. Bring down two zeros to make it 100.
- Double the divisor (2) to get 4, and determine the next digit by trial to get a product less than or equal to 100. Here, 42 x 2 = 84.
- Subtract 84 from 100 to get a remainder of 16. Bring down two more zeros to make it 1600.
- Continue this process until you reach the desired precision. The next steps give the digits of the square root in sequence.
Following these steps, we find:
| Step | Operation | Result |
| 1 | 5.00000000 ÷ 2 | 2.236... |
| 2 | Subtract 4 (22) | 1.00000000 |
| 3 | Bring down 00 to get 100 | 100 ÷ 42 |
| 4 | 42 × 2 = 84 | Subtract 84 from 100 |
| 5 | Remainder 16, bring down 00 | 1600 |
| 6 | Double 42 to get 84, next digit trial | ... |
The process continues, giving the square root of 5 approximately as 2.2360 to four decimal places.
Summary
The square root of 5, calculated using the long division method, is approximately 2.236. This method is systematic and useful for finding the square roots of non-perfect squares with high precision.

Square Root of 5 in Decimal Form
The square root of 5, represented as \( \sqrt{5} \), is an irrational number. Its decimal form is non-repeating and non-terminating. The value of \( \sqrt{5} \) in decimal form, rounded to 15 decimal places, is approximately:
\[
\sqrt{5} \approx 2.2360679774998
\]
To provide a more detailed understanding, let's explore how this value is obtained and its properties:
Decimal Expansion
The decimal expansion of \( \sqrt{5} \) is as follows:
\[
\sqrt{5} = 2.2360679774997896964091736687312762354406183596115257242708972454\ldots
\]
This expansion continues infinitely without repeating.
Calculation Methods
There are several methods to calculate the decimal value of \( \sqrt{5} \), including:
- Long Division Method: A manual method of finding square roots by approximation.
- Newton's Method (Heron's Method): An iterative numerical method that starts with an initial guess and refines it.
Long Division Method
Here is a step-by-step process for calculating \( \sqrt{5} \) using the long division method:
- Start by grouping the digits in pairs from the decimal point. For 5, it is 5.00 00 00...
- Find the largest number whose square is less than or equal to 5, which is 2 (since \( 2^2 = 4 \)).
- Subtract 4 from 5 to get 1. Bring down a pair of zeros to make it 100.
- Double the number obtained (2) to get 4, and determine how many times 4 fits into 100. The answer is 2 (since \( 42 \times 2 = 84 \)).
- Continue this process to get further decimal places.
Applications
The square root of 5 is used in various mathematical and scientific applications, such as:
- Geometry: Calculating the diagonal of a rectangle with sides in a 1:2 ratio.
- Algebra: Solving quadratic equations where the discriminant involves 5.
Conclusion
Understanding the decimal form of \( \sqrt{5} \) helps in various mathematical computations and applications. Its non-repeating, non-terminating nature is a key characteristic of irrational numbers, reflecting the complexity and beauty of mathematics.
Applications of the Square Root of 5
The square root of 5, denoted as √5, finds various applications in different fields of mathematics, science, engineering, and even art. Its unique properties make it a valuable constant in numerous theoretical and practical contexts.
1. Mathematics
- Golden Ratio: The square root of 5 is instrumental in the calculation of the golden ratio (φ), which is expressed as:
\[\phi = \frac{1 + \sqrt{5}}{2}\]
The golden ratio appears in various geometric constructions and number theory problems.
- Fibonacci Sequence: The square root of 5 plays a role in the closed-form expression of the Fibonacci sequence, known as Binet's formula:
\[F(n) = \frac{1}{\sqrt{5}} \left( \left( \frac{1 + \sqrt{5}}{2} \right)^n - \left( \frac{1 - \sqrt{5}}{2} \right)^n \right)\]
This formula provides a direct method to calculate Fibonacci numbers without iterative computation.
2. Geometry
- Pentagons and Pentagrams: The length ratios in regular pentagons and pentagrams are connected to the square root of 5. Specifically, the diagonal-to-side ratio of a regular pentagon is given by:
\[\frac{1 + \sqrt{5}}{2}\]
- Golden Rectangles: Rectangles whose side lengths are in the golden ratio are called golden rectangles. These rectangles can be split into squares and smaller golden rectangles, demonstrating a recursive property that involves √5.
3. Physics and Engineering
- Structural Analysis: In engineering, the square root of 5 can be relevant in the calculation of natural frequencies and modal analysis of structures, where the eigenvalues of certain matrices involve √5.
- Acoustics: The square root of 5 may appear in formulas related to wave propagation and resonance frequencies in various physical media.
4. Art and Architecture
- Design Proportions: The aesthetic appeal of the golden ratio, which incorporates the square root of 5, is used in art and architectural design to achieve visually pleasing proportions.
- Historical Constructions: Many ancient structures, such as the Parthenon and the Pyramids, are believed to incorporate proportions related to the golden ratio, indirectly involving √5.
5. Technology
- Algorithm Design: Algorithms in computer science, particularly those involving recursive structures or optimization problems, might utilize the golden ratio and its properties, which depend on √5.
- Cryptography: Certain cryptographic algorithms and pseudorandom number generators may rely on mathematical constants like √5 to enhance security and unpredictability.
Conclusion
The square root of 5 is a fundamental mathematical constant with diverse applications across various disciplines. Its role in the golden ratio, Fibonacci sequence, and geometric constructions underscores its importance in both theoretical and practical contexts, while its influence extends to art, architecture, engineering, and technology.
Square Root of 5 in Geometry
The square root of 5 (\(\sqrt{5}\)) appears frequently in geometric constructions and can be visualized through various geometric methods. One of the most common methods is using the double square.
Double Square Construction
A double square is a rectangle where one side is twice the length of the other side. For example, if the shorter side is 1 unit, the longer side is 2 units. The diagonal of this double square is equal to \(\sqrt{5}\). This relationship can be visualized as follows:
- Draw a line segment \(AB\) of length 1 unit.
- Extend \(AB\) to point \(C\) such that \(BC\) is also 1 unit, making \(AC\) a segment of length 2 units.
- Draw a perpendicular line from point \(C\), creating a right angle with line \(AC\).
- Draw a line segment \(CD\) perpendicular to \(AC\) with length 1 unit.
- Complete the rectangle by drawing line segment \(AD\).
The diagonal \(AD\) of this rectangle is the square root of 5 (\(\sqrt{5}\)). This is because in a right-angled triangle with sides of length 1 and 2, the hypotenuse is \(\sqrt{5}\), derived from the Pythagorean theorem:
\( \sqrt{1^2 + 2^2} = \sqrt{1 + 4} = \sqrt{5} \)
Applications in Sacred Geometry
The concept of the square root of 5 is not only important in basic geometric constructions but also in sacred geometry. It is found in historical structures such as Solomon's Temple and the King's Chamber of the Great Pyramid. These structures often incorporate the proportions of the double square, utilizing the diagonal length of \(\sqrt{5}\) to symbolize harmony and balance.
Example in Modern Geometry
In modern geometry, the square root of 5 can be visualized using compass and straightedge constructions:
- Draw a line segment \(AB\) of length 1 unit.
- Construct a perpendicular bisector of \(AB\) at point \(M\), the midpoint of \(AB\).
- Draw a semicircle with center \(M\) and radius \(1.5\) units (since \(M\) is 0.5 units from \(A\) and \(B\), the total length is 2 units).
- Extend line segment \(AB\) to point \(C\) such that \(BC\) is 1 unit.
- The intersection of the semicircle with the perpendicular line from \(B\) at \(D\) provides a segment \(BD\) of length \(\sqrt{5}\).
Conclusion
The square root of 5 is a significant number in both theoretical and applied geometry, appearing in various constructions and symbolic representations. Its applications range from basic geometric constructions to complex architectural designs, reflecting its importance in mathematics and beyond.
Square Root of 5 in Algebra
In algebra, the square root of 5 is often represented using the radical symbol as √5. This notation signifies a number which, when multiplied by itself, results in 5.
The square root of 5 can be involved in various algebraic expressions and equations. Here are some key aspects:
- Basic Representation:
The equation \( x^2 = 5 \) has two solutions: \( x = \sqrt{5} \) and \( x = -\sqrt{5} \). This demonstrates that both the positive and negative square roots are valid solutions.
- Simplifying Expressions:
When simplifying expressions involving square roots, it's useful to remember properties such as:
\[
\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}
\]
This allows for the simplification of expressions like:
\[
\sqrt{20} = \sqrt{4 \cdot 5} = \sqrt{4} \cdot \sqrt{5} = 2\sqrt{5}
\] - Rationalizing the Denominator:
Rationalizing the denominator involves eliminating the square root from the denominator of a fraction. For example, to rationalize:
\[
\frac{1}{\sqrt{5}}
\]
Multiply both the numerator and the denominator by \( \sqrt{5} \):
\[
\frac{1}{\sqrt{5}} \cdot \frac{\sqrt{5}}{\sqrt{5}} = \frac{\sqrt{5}}{5}
\] - Solving Quadratic Equations:
Quadratic equations of the form \( ax^2 + bx + c = 0 \) can have solutions that involve the square root of 5. For instance:
\[
x^2 - 5 = 0
\]
Solving for \( x \) gives:
\[
x = \pm\sqrt{5}
\]
Understanding these concepts helps in solving a variety of algebraic problems that involve the square root of 5.

Historical Context of the Square Root of 5
The historical journey of understanding the square root of 5 dates back to ancient civilizations. The knowledge and computation of square roots, including that of 5, have evolved significantly over time.
In ancient Babylon, around 2000 BCE, mathematicians used clay tablets to perform calculations involving square roots. They developed methods to approximate square roots using iterative algorithms, some of which likely included values close to the square root of 5.
The Greeks, especially during the time of Pythagoras (circa 570–495 BCE), made substantial contributions to the understanding of square roots. Pythagorean mathematicians explored irrational numbers, which include the square root of 5. The Pythagorean theorem, expressed as \(a^2 + b^2 = c^2\), was crucial in geometric interpretations of square roots.
Euclid, in his seminal work "Elements" (circa 300 BCE), formalized much of the geometry that includes the properties of square roots. While Euclid's focus was primarily on geometric constructions and the relationships between different geometric entities, his work laid the foundation for later mathematicians to explore irrational numbers in more depth.
During the Islamic Golden Age (8th to 14th centuries), scholars like Al-Khwarizmi expanded on Greek mathematics and introduced algebraic methods to calculate square roots. The square root of 5 was among the many irrational numbers they studied, and their work greatly influenced later European mathematicians.
In the Renaissance period, mathematicians such as Fibonacci brought Arabic mathematical knowledge to Europe. Fibonacci's "Liber Abaci" (1202) included methods for calculating square roots, contributing to the broader understanding and computation of values like the square root of 5.
The development of modern algebra and the formalization of real numbers in the 19th century further cemented the understanding of irrational numbers. Mathematicians like Dedekind and Cantor developed theories that included rigorous definitions and properties of square roots, ensuring the precise computation of the square root of 5 as we know it today.
The historical context of the square root of 5 illustrates a rich tapestry of mathematical development, spanning ancient Babylonian clay tablets to modern algebraic theory. This journey highlights the collaborative and cumulative nature of mathematical discovery.
Square Root of 5 in Modern Mathematics
The square root of 5, denoted as \( \sqrt{5} \), plays a significant role in various modern mathematical contexts. It is an irrational number, approximately equal to 2.236, and it appears in several advanced mathematical theories and applications.
One of the most prominent areas where \( \sqrt{5} \) is encountered is in the study of the golden ratio, \( \phi \), which is expressed as:
\[
\phi = \frac{1 + \sqrt{5}}{2}
\]
The golden ratio has numerous applications in art, architecture, and nature, creating aesthetically pleasing proportions and patterns.
In algebra, the square root of 5 is used in solving quadratic equations. For instance, the quadratic equation:
\[
x^2 - 5 = 0
\]
has solutions:
\[
x = \pm \sqrt{5}
\]
This showcases its fundamental presence in polynomial equations and their roots.
The square root of 5 also appears in various approximation methods. One such method is the continued fraction representation, which provides an effective way to approximate \( \sqrt{5} \) with rational numbers:
\[
\sqrt{5} = [2; 4, 4, 4, \ldots]
\]
This continued fraction reveals the periodicity and helps in precise computations.
In linear algebra, the eigenvalues of certain matrices can include \( \sqrt{5} \). For example, the Fibonacci sequence can be represented using matrix exponentiation, where the eigenvalues of the transformation matrix involve \( \sqrt{5} \):
\[
\begin{pmatrix}
1 & 1 \\
1 & 0
\end{pmatrix}
\]
This matrix has eigenvalues:
\[
\lambda = \frac{1 \pm \sqrt{5}}{2}
\]
highlighting the intrinsic link between the Fibonacci sequence and the golden ratio.
Furthermore, in numerical analysis, methods like Newton's iteration are used to approximate \( \sqrt{5} \). Starting with an initial guess \( x_0 \), the iteration:
\[
x_{n+1} = \frac{x_n + \frac{5}{x_n}}{2}
\]
rapidly converges to \( \sqrt{5} \), demonstrating the efficiency of modern computational techniques.
Overall, the square root of 5 is deeply embedded in various branches of modern mathematics, from algebra and number theory to numerical methods and matrix algebra. Its applications continue to influence contemporary mathematical research and practical computations.
Common Misconceptions about the Square Root of 5
Understanding the square root of 5 can be tricky, and there are several common misconceptions that students often encounter. Addressing these misconceptions is crucial for a solid grasp of the concept. Here are some of the most frequent misunderstandings:
-
Misconception 1: Square Root of a Sum
One of the most common mistakes is assuming that the square root of a sum is equal to the sum of the square roots. Specifically, some might think that:
\[\sqrt{5 + x} = \sqrt{5} + \sqrt{x}\]
This is incorrect. The correct approach is to first add the numbers under the square root and then take the square root of the result.
-
Misconception 2: Rationalizing the Square Root
Another misconception is the belief that the square root of 5 can be expressed as a simple fraction. In reality, \(\sqrt{5}\) is an irrational number, meaning it cannot be expressed as a ratio of two integers. Its decimal representation is non-terminating and non-repeating:
\[\sqrt{5} \approx 2.236\]
-
Misconception 3: Simplifying Square Roots
Some students incorrectly assume that the square root of a product can be simplified without consideration. For instance, they might think:
\[\sqrt{25 \times 5} = 5 \sqrt{5}\]
The correct approach is to factor the product first and then simplify:
\[\sqrt{25 \times 5} = \sqrt{125} = 5 \sqrt{5}\]
-
Misconception 4: Negative Square Roots
There's often confusion around the concept of negative square roots. While \(\sqrt{5}\) is positive, students might incorrectly assume that \(-\sqrt{5}\) is a different entity. However, \(-\sqrt{5}\) simply represents the negative of the positive square root of 5.
By recognizing and addressing these misconceptions, students can better understand the properties and behavior of square roots in mathematical contexts.
Square Root of 5 in Technology and Engineering
The square root of 5 has various applications in technology and engineering, demonstrating its significance beyond theoretical mathematics. Here are some notable uses:
- Signal Processing: In signal processing, particularly in digital communications and audio processing, calculations involving square roots of numbers like 5 are utilized for modulation schemes and filtering algorithms.
- Electrical Engineering: It plays a role in impedance calculations for circuits and in determining resonant frequencies of components, aiding in the design and optimization of electrical systems.
- Computer Graphics: Algorithms for computer graphics often involve square roots, including calculations related to geometric transformations and 3D rendering, enhancing realism in visual simulations.
- Structural Engineering: Engineers use square roots in structural analysis, such as determining critical loads and stresses in materials, ensuring the safety and durability of buildings and bridges.
- Fluid Dynamics: Applications in fluid dynamics utilize square roots for calculating flow rates, pressure differentials, and other parameters crucial for designing efficient hydraulic systems.
Understanding the properties and mathematical behavior of the square root of 5 enables engineers and technologists to innovate and solve complex problems across various disciplines.

Visualizing the Square Root of 5
Visualizing the square root of 5 involves understanding its geometric representation and its implications across various contexts:
- Geometric Interpretation: In a geometric context, the square root of 5 represents the length of the diagonal of a square whose sides have a length of 5 units. This diagonal connects opposite corners of the square, illustrating a fundamental geometric relationship.
- Graphical Representation: Graphically, the square root of 5 can be depicted on a number line approximately between 2.2 and 2.3, highlighting its position among other square roots and its numerical proximity to integer values.
- Visual Applications: Artists and designers use the square root of 5 in the Golden Ratio, a mathematical proportion considered aesthetically pleasing, influencing compositions in art, architecture, and design.
- Mathematical Patterns: Exploring mathematical patterns, such as continued fractions and series expansions, reveals the intricate nature of the square root of 5 and its connections to other mathematical constants and sequences.
By visualizing the square root of 5, individuals can appreciate its role in geometry, art, and mathematical theory, enhancing understanding and creativity in diverse fields.
Advanced Topics Related to the Square Root of 5
The square root of 5, denoted as \( \sqrt{5} \), is an irrational number that has fascinated mathematicians for centuries. This section delves into some advanced mathematical concepts and theories related to \( \sqrt{5} \).
1. Continued Fraction Expansion
The continued fraction expansion of \( \sqrt{5} \) provides a way to represent this irrational number as an infinite sequence of fractions. The continued fraction for \( \sqrt{5} \) is:
\[
\sqrt{5} = 2 + \cfrac{1}{4 + \cfrac{1}{4 + \cfrac{1}{4 + \ddots}}}
\]
Understanding the structure of continued fractions can help in approximating \( \sqrt{5} \) more accurately.
2. Golden Ratio Connection
The square root of 5 is closely related to the Golden Ratio, \( \varphi \). The Golden Ratio is defined as:
\[
\varphi = \frac{1 + \sqrt{5}}{2}
\]
This connection appears in various areas of mathematics and nature, including Fibonacci sequences and pentagonal geometry.
3. Pell's Equation
Pell's equation is a famous Diophantine equation of the form \( x^2 - Dy^2 = 1 \), where \( D \) is a non-square integer. For \( \sqrt{5} \), Pell's equation can be expressed as:
\[
x^2 - 5y^2 = 1
\]
Solutions to this equation are closely linked to the properties of \( \sqrt{5} \), with solutions given by pairs of integers \( (x, y) \).
4. Conjugate and Algebraic Form
In algebra, \( \sqrt{5} \) can be expressed in terms of its conjugate. If we denote the conjugate of \( \sqrt{5} \) as \( -\sqrt{5} \), then any expression involving \( \sqrt{5} \) can also involve its conjugate. For example, the polynomial \( x^2 - 5 = 0 \) has roots \( \sqrt{5} \) and \( -\sqrt{5} \).
5. Quadratic Field Extensions
The number \( \sqrt{5} \) generates a quadratic field extension over the rational numbers. This field, denoted \( \mathbb{Q}(\sqrt{5}) \), consists of all numbers of the form \( a + b\sqrt{5} \) where \( a \) and \( b \) are rational numbers. This field has interesting properties in algebra and number theory.
6. Applications in Linear Algebra
In linear algebra, \( \sqrt{5} \) appears in eigenvalue problems and matrix computations. For instance, consider the matrix:
\[
\begin{pmatrix}
2 & 1 \\
1 & 2
\end{pmatrix}
\]
This matrix has eigenvalues \( 3 \) and \( 1 \), but modifying it slightly can introduce \( \sqrt{5} \) into its eigenvalues.
7. Periodic Orbits in Dynamical Systems
The value \( \sqrt{5} \) can also appear in the study of dynamical systems, particularly in the analysis of periodic orbits and chaos. Systems with symmetry or certain periodic structures can have solutions involving \( \sqrt{5} \).
8. Advanced Geometric Applications
In advanced geometry, \( \sqrt{5} \) plays a role in the dimensions of certain polygons and polyhedra. For instance, in a regular pentagon, the diagonal to side ratio involves \( \sqrt{5} \) as part of the Golden Ratio.
Exploring these advanced topics reveals the depth and breadth of the mathematical significance of the square root of 5. From number theory to geometry, \( \sqrt{5} \) continues to inspire and challenge mathematicians.
Conclusion: Importance of Understanding the Square Root of 5
The square root of 5, denoted as √5, holds a significant place in mathematics and various real-world applications. Understanding this irrational number provides insight into the relationship between numbers and their properties, which is crucial for advanced mathematical concepts.
Firstly, √5 is an irrational number, meaning it cannot be expressed as a simple fraction. This property alone opens up discussions about the nature of numbers and their classifications, highlighting the complexities and beauty of mathematical structures. The irrational nature of √5 also exemplifies the richness of number theory and its implications in algebra and calculus.
Moreover, √5 plays a pivotal role in geometry. It is the length of the diagonal of a rectangle with sides 1 and 2, which is derived from the Pythagorean theorem. This geometric representation is fundamental in understanding various properties of shapes and forms the basis for more complex geometric constructions. The square root of 5 is also integral to the golden ratio, φ, where φ = (1 + √5)/2, which is prevalent in art, architecture, and nature.
The square root of 5 is also essential in algebra, especially in solving quadratic equations and in the study of polynomial roots. Its presence in the quadratic formula highlights its importance in finding solutions to equations that model real-world scenarios. This knowledge is crucial for students and professionals dealing with mathematical modeling and problem-solving in various fields.
In the realm of modern mathematics, √5 appears in advanced topics such as continued fractions and series. It is involved in the closed-form expression for Fibonacci numbers, illustrating its relevance in sequences and series that model growth patterns and natural phenomena.
Furthermore, √5 has practical applications in technology and engineering. Understanding this value is vital in designing algorithms for computing, optimizing engineering designs, and solving real-world problems that require precise calculations and measurements.
In conclusion, the square root of 5 is not just a mathematical curiosity; it is a fundamental component of various mathematical theories and practical applications. Mastery of this concept can lead to a deeper appreciation of the interconnectedness of mathematical ideas and their impact on the world around us.
Video này giải thích cách đơn giản hóa căn bậc hai của 5, cung cấp hướng dẫn chi tiết và dễ hiểu cho người xem.
Căn Bậc Hai Của 5 Đơn Giản
READ MORE:
Video này hướng dẫn cách tìm căn bậc hai của 5 bằng phương pháp chia dài, cung cấp các bước chi tiết và dễ hiểu.
Cách Tìm Căn Bậc Hai của 5 bằng Phương Pháp Chia Dài / Căn Bậc Hai của 5 / Tìm Căn Bậc Hai của 5