Topic what are the square roots of 9: Curious about the square roots of 9? You're in the right place! In this article, we'll explore the concept of square roots, focusing on the number 9. Learn why 9 has two square roots and how they are determined, making mathematics both fascinating and accessible.
Table of Content
- Square Roots of 9
- Introduction
- Definition of Square Roots
- Mathematical Calculation
- Positive and Negative Square Roots
- Understanding the Square Root Symbol
- Properties of Square Roots
- Why 9 has Two Square Roots
- Square Roots in Different Mathematical Fields
- Applications of Square Roots in Real Life
- Visual Representation of Square Roots
- Frequently Asked Questions
- Conclusion
- YOUTUBE: Video giải thích về căn bậc hai của số âm – 9, với cách tiếp cận chi tiết và dễ hiểu để thu hút người xem.
Square Roots of 9
The square root of a number \(x\) is a number \(y\) such that \(y^2 = x\). In this case, we are finding the square roots of 9.
Calculation
To find the square roots of 9, we solve the equation:
\[ y^2 = 9 \]
There are two values of \(y\) that satisfy this equation:
- \( y = 3 \)
- \( y = -3 \)
Therefore, the square roots of 9 are:
\[ \sqrt{9} = 3 \quad \text{and} \quad \sqrt{9} = -3 \]
Explanation
This happens because squaring either 3 or -3 results in 9:
- \( 3^2 = 3 \times 3 = 9 \)
- \( (-3)^2 = (-3) \times (-3) = 9 \)
Summary
In conclusion, the two square roots of 9 are:
- Positive square root: \( 3 \)
- Negative square root: \( -3 \)
READ MORE:
Introduction
The concept of square roots is fundamental in mathematics, providing a foundation for understanding various algebraic and geometric principles. The square root of a number \(x\) is a value \(y\) such that \(y^2 = x\). In this context, we will focus on the square roots of 9.
To understand the square roots of 9, let's break down the process step by step:
- Identify the number: Here, our number is 9.
- Understand the equation: We need to find a number \(y\) such that \(y^2 = 9\).
- Solve the equation: There are two solutions to this equation because both positive and negative numbers, when squared, can result in a positive number.
Hence, the solutions to the equation \(y^2 = 9\) are:
- \( y = 3 \)
- \( y = -3 \)
This means that the square roots of 9 are 3 and -3. These roots play a significant role in various mathematical contexts, including solving quadratic equations and analyzing functions.
Definition of Square Roots
A square root of a number is a value that, when multiplied by itself, gives the original number. Mathematically, if \(y\) is the square root of \(x\), then \(y^2 = x\). The square root is denoted by the radical symbol \( \sqrt{} \).
For example, consider the number 9:
- Identify the number: 9
- Set up the equation: \( y^2 = 9 \)
- Find the solutions: The values of \(y\) that satisfy this equation are the square roots of 9.
There are two solutions because both positive and negative values can be squared to result in the original number:
- \( 3^2 = 9 \)
- \( (-3)^2 = 9 \)
Therefore, the square roots of 9 are:
- \( \sqrt{9} = 3 \)
- \( \sqrt{9} = -3 \)
This duality is a fundamental property of square roots, showing that each positive number has two square roots: one positive and one negative.
Mathematical Calculation
Finding the square roots of a number involves determining the values that, when squared, equal the original number. For the number 9, we follow these steps:
- Identify the number: We are working with the number 9.
- Set up the equation: We need to solve for \(y\) in the equation \( y^2 = 9 \).
- Solve the equation: Determine the values of \(y\) that satisfy the equation.
The equation \( y^2 = 9 \) implies that \( y \) can be either positive or negative. We solve for \( y \) as follows:
- Take the positive square root: \( y = \sqrt{9} = 3 \)
- Take the negative square root: \( y = -\sqrt{9} = -3 \)
Thus, the solutions to the equation are \( y = 3 \) and \( y = -3 \).
We can verify these solutions by squaring them:
- \( 3^2 = 3 \times 3 = 9 \)
- \( (-3)^2 = (-3) \times (-3) = 9 \)
This confirms that both 3 and -3 are indeed the square roots of 9. In summary, the mathematical calculation shows that the number 9 has two square roots: \( \pm 3 \).
Positive and Negative Square Roots
Understanding the concept of square roots involves recognizing that each positive number has both a positive and a negative square root. For the number 9, the square roots are 3 and -3. Let's explore this in detail:
- Identify the number: The number we are examining is 9.
- Set up the equation: We solve for \(y\) in the equation \( y^2 = 9 \).
- Solve for \(y\): The solutions are determined by taking both the positive and negative roots of 9.
The mathematical process involves the following steps:
- Take the positive square root: \( y = \sqrt{9} = 3 \)
- Take the negative square root: \( y = -\sqrt{9} = -3 \)
This yields two solutions: \( y = 3 \) and \( y = -3 \).
To understand why both values are valid, consider the property of squaring numbers:
- When we square 3, we get: \( 3 \times 3 = 9 \)
- When we square -3, we get: \( (-3) \times (-3) = 9 \)
Both calculations result in the original number 9, demonstrating that 9 has two square roots.
This concept is fundamental in mathematics, highlighting the dual nature of square roots. Positive and negative roots are crucial in solving quadratic equations and in various applications across different fields of study.
In summary, the number 9 has two square roots: 3 (positive) and -3 (negative). This duality is an essential aspect of understanding square roots and their properties.

Understanding the Square Root Symbol
The square root symbol \( \sqrt{} \) is a fundamental mathematical notation used to denote the square root of a number. Let's explore its meaning and application in detail.
- Definition: The square root of a number \( x \) is a value \( y \) such that \( y^2 = x \). It is represented as \( \sqrt{x} \).
- Positive Root: The principal (positive) square root of \( x \) is written as \( \sqrt{x} \). For example, \( \sqrt{9} = 3 \).
- Negative Root: The negative square root of \( x \) is written as \( -\sqrt{x} \). For example, \( -\sqrt{9} = -3 \).
Let's break down the symbol and its use step by step:
- The radical symbol \( \sqrt{} \) indicates the square root operation.
- The number under the radical sign is called the radicand. In \( \sqrt{9} \), 9 is the radicand.
- The square root symbol always implies two roots: a positive root and a negative root, unless specified otherwise.
For the number 9:
- The positive square root is \( \sqrt{9} = 3 \).
- The negative square root is \( -\sqrt{9} = -3 \).
This means that \( \sqrt{9} \) can represent both 3 and -3, although conventionally, \( \sqrt{9} \) usually refers to the principal (positive) square root.
In mathematical expressions, the square root symbol is used to simplify and solve equations involving square roots. It is also essential in various fields such as algebra, geometry, and calculus.
Understanding the square root symbol and its implications helps in comprehending more complex mathematical concepts and solving a wide range of mathematical problems.
Properties of Square Roots
Square roots possess several important properties that are fundamental to understanding their behavior in mathematics. These properties make square roots useful in a wide range of mathematical applications.
- Non-negativity: The principal square root of a non-negative number is always non-negative. For any \( x \geq 0 \), \( \sqrt{x} \geq 0 \).
- Product Property: The square root of a product is the product of the square roots. For any non-negative numbers \( a \) and \( b \), \( \sqrt{ab} = \sqrt{a} \cdot \sqrt{b} \).
- Quotient Property: The square root of a quotient is the quotient of the square roots. For any non-negative numbers \( a \) and \( b \), with \( b \neq 0 \), \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \).
- Power Property: The square root of a number raised to a power can be expressed as the number raised to half the power. For any non-negative number \( x \) and any real number \( n \), \( \sqrt{x^n} = x^{n/2} \).
- Sum and Difference Property: Unlike products and quotients, the square root of a sum or difference is not generally equal to the sum or difference of the square roots. \( \sqrt{a + b} \neq \sqrt{a} + \sqrt{b} \) and \( \sqrt{a - b} \neq \sqrt{a} - \sqrt{b} \).
For the number 9, these properties can be illustrated as follows:
- Non-negativity: \( \sqrt{9} = 3 \), which is non-negative.
- Product Property: \( \sqrt{9 \cdot 1} = \sqrt{9} \cdot \sqrt{1} = 3 \cdot 1 = 3 \).
- Quotient Property: \( \sqrt{\frac{9}{1}} = \frac{\sqrt{9}}{\sqrt{1}} = \frac{3}{1} = 3 \).
- Power Property: \( \sqrt{9^1} = 9^{1/2} = 3 \).
These properties highlight the consistency and utility of square roots in mathematical calculations, providing a basis for solving equations and understanding relationships between numbers.
Why 9 has Two Square Roots
In mathematics, a number can have two square roots because squaring a positive number or its negative counterpart yields the same positive result. This is why the number 9 has both a positive and a negative square root. Let's explore this concept step by step:
- Understanding Squaring: Squaring a number means multiplying it by itself. For example, \( 3 \times 3 = 9 \) and \( -3 \times -3 = 9 \).
- Equation Setup: To find the square roots of 9, we solve the equation \( y^2 = 9 \).
- Solving the Equation: The solutions to the equation are the numbers that, when squared, give 9. This results in two solutions: \( y = 3 \) and \( y = -3 \).
The mathematical reason for having two square roots is based on the properties of real numbers and their behavior under squaring:
- Positive Root: When \( y = 3 \), \( 3^2 = 9 \).
- Negative Root: When \( y = -3 \), \( (-3)^2 = 9 \).
This duality is a fundamental characteristic of square roots, reflecting the symmetry of the squaring function:
- Both positive and negative numbers, when squared, result in a positive value.
- This symmetry means that for any positive number, there are always two square roots: one positive and one negative.
For the number 9, this means:
- The positive square root is \( \sqrt{9} = 3 \).
- The negative square root is \( -\sqrt{9} = -3 \).
In summary, 9 has two square roots because both 3 and -3, when squared, equal 9. This dual nature of square roots is a key concept in understanding and solving quadratic equations and other mathematical problems.
Square Roots in Different Mathematical Fields
Square roots play a significant role in various branches of mathematics. Below, we explore their applications and importance in different mathematical fields:
1. Algebra
In algebra, square roots are fundamental in solving quadratic equations. The general form of a quadratic equation is:
\[ ax^2 + bx + c = 0 \]
To solve for \( x \), we often use the quadratic formula:
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
The square root here is crucial for finding the roots of the equation, which can be real or complex numbers.
2. Geometry
In geometry, the concept of square roots is used to determine the lengths of sides in right-angled triangles, thanks to the Pythagorean theorem:
\[ a^2 + b^2 = c^2 \]
Where \( c \) is the hypotenuse. To find \( c \), we take the square root:
\[ c = \sqrt{a^2 + b^2} \]
3. Calculus
Square roots appear in calculus in various contexts, such as in integrals and derivatives. For example, when dealing with arc lengths or areas, expressions often involve square roots:
\[ \text{Arc Length} = \int_a^b \sqrt{1 + \left( \frac{dy}{dx} \right)^2} \, dx \]
This integral calculates the length of a curve, where the square root ensures we account for the distance properly.
4. Complex Numbers
Square roots extend to complex numbers, where they help define operations and properties. For a complex number \( z \), its square root involves both real and imaginary parts:
\[ \sqrt{z} = \sqrt{a + bi} = \sqrt{r} \left( \cos \frac{\theta}{2} + i \sin \frac{\theta}{2} \right) \]
where \( r \) is the modulus of \( z \) and \( \theta \) is the argument.
5. Linear Algebra
In linear algebra, square roots are used in matrix operations, such as finding the square root of a matrix. This involves finding a matrix \( B \) such that:
\[ B^2 = A \]
where \( A \) is the given matrix. Square roots of matrices are important in areas like quantum mechanics and stability analysis.
6. Number Theory
In number theory, square roots are essential for understanding properties of integers. For instance, solving congruences involving squares often requires finding modular square roots:
\[ x^2 \equiv n \pmod{p} \]
This is crucial in cryptographic algorithms like RSA, where square roots modulo a prime play a role in key generation and encryption/decryption processes.
7. Differential Equations
Square roots appear in solutions to differential equations, especially in characteristic equations for linear differential equations. For a second-order differential equation:
\[ ay'' + by' + cy = 0 \]
We solve the characteristic equation:
\[ ar^2 + br + c = 0 \]
The solutions, which may involve square roots, help determine the general solution to the differential equation.
Conclusion
The concept of square roots is pervasive in mathematics, influencing various fields and applications. From solving equations to analyzing complex systems, square roots are a fundamental mathematical tool.

Applications of Square Roots in Real Life
The concept of square roots extends beyond pure mathematics and finds various practical applications in different fields. Here are some key examples:
- Engineering and Physics
Square roots are frequently used in engineering and physics to solve problems involving area, volume, and rates. For instance, in physics, the square root function is used to determine the root mean square (RMS) values, which are essential in understanding alternating current (AC) circuits.
- Architecture and Construction
Architects and construction workers use square roots to calculate the dimensions of structures. For example, if they need to find the side length of a square area given its total area, they use the square root.
- Computer Science
In computer algorithms, especially those related to graphics and machine learning, square roots are used to normalize data and in distance calculation algorithms, such as the Euclidean distance in clustering algorithms.
- Finance
Square roots are used in finance to calculate the volatility of stocks and in the computation of various financial metrics. For example, the standard deviation, a measure of volatility, involves taking the square root of the variance.
- Astronomy
Square roots help astronomers calculate distances between celestial bodies. For example, the inverse square law, which describes the intensity of gravitational and electromagnetic forces, involves square root calculations.
- Medicine
Square roots are applied in medical research and pharmacology, particularly in dosages calculations and in the statistical analysis of medical data.
- Everyday Use
Square roots are used in daily life activities, such as determining the size of a television screen or any other square or rectangular area, as well as in various DIY projects that require precise measurements.
The ability to understand and apply square roots is essential in many practical situations, making it a valuable mathematical concept.
Visual Representation of Square Roots
Understanding the square roots of numbers can be greatly enhanced through visual representations. Here are some methods to visualize the square roots, particularly focusing on the square roots of 9.
Number Line Representation
One straightforward way to visualize square roots is by using a number line. The square root of 9, which are 3 and -3, can be marked on the number line as follows:
- Locate 0 on the number line.
- Mark points 3 units to the right of 0 and 3 units to the left of 0.
This shows that the square root of 9 is both 3 and -3.
Geometric Square Representation
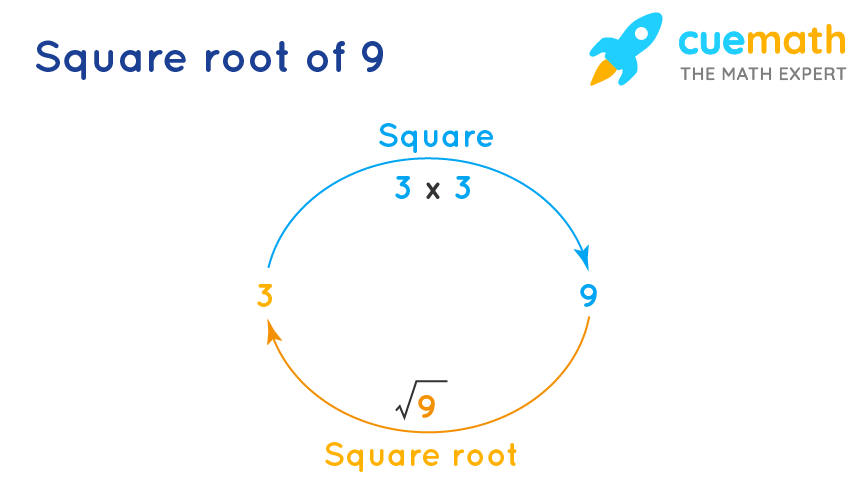
Another effective method is to use geometric shapes. Since the square root of a number is the length of the side of a square with that area, we can represent the square root of 9 as follows:
- Draw a square with an area of 9 square units.
- Each side of this square will measure 3 units, visually demonstrating that \( \sqrt{9} = 3 \).
This method is particularly helpful for understanding the concept of square roots in a tangible way.
Graphical Representation
Graphing the function \( y = \sqrt{x} \) provides another visual approach:
In a Cartesian coordinate system, plot the function \( y = \sqrt{x} \). The point (9, 3) will lie on this curve, showing that the square root of 9 is 3.
Similarly, you can plot \( y = -\sqrt{x} \), where the point (9, -3) will illustrate that the negative square root of 9 is -3.
This method helps in understanding how square roots behave in different quadrants of the graph.
Visualizing Through Prime Factorization
Using prime factorization to visualize square roots can also be effective. For the number 9:
- Prime factorize 9 to get \( 9 = 3 \times 3 \).
- The square root of 9 is obtained by taking one factor from each pair, which gives \( \sqrt{9} = 3 \).
This method shows how the components of the number combine to form its square root.
Interactive Tools and Software
There are several online tools and software that can provide dynamic visualizations of square roots. These tools often allow users to manipulate the numbers and see the corresponding changes in the graphical or geometric representations. This interactive approach can deepen understanding and engagement with the concept of square roots.
Overall, visual representations are powerful tools for grasping the concept of square roots. By using number lines, geometric squares, graphs, and prime factorization, we can develop a more comprehensive understanding of square roots and their properties.
Frequently Asked Questions
Here are some common questions and detailed answers regarding the square roots of 9:
-
What is the value of the square root of 9?
The square root of 9 is ±3. Mathematically, it can be expressed as √9 = ±3 because both 3 and -3 when squared (3² and (-3)²) give 9.
-
Why does 9 have two square roots?
The number 9 has two square roots, 3 and -3, because squaring either 3 or -3 results in 9. This is due to the property of multiplication where the product of two negative numbers is positive.
-
Is the square root of 9 a rational number?
Yes, the square root of 9 is a rational number. This is because 9 is a perfect square, and its square roots, 3 and -3, are both integers. Rational numbers are numbers that can be expressed as the quotient of two integers.
-
What is the square root of 9/49?
The square root of 9/49 is calculated as √(9/49) = √9 / √49 = 3/7. Thus, √(9/49) = 3/7.
-
What is the square of the square root of 9?
The square of the square root of 9 is the number 9 itself. This is because squaring the square root of a number returns the original number: (√9)² = 9.
-
What is the square root of -9?
The square root of -9 is an imaginary number. It is written as √-9 = 3i, where i is the imaginary unit (√-1).
-
What is the value of 9 times the square root of 9?
The value of 9 times the square root of 9 is calculated as 9 * √9 = 9 * 3 = 27.
Conclusion
The square roots of 9, which are 3 and -3, play a fundamental role in various mathematical contexts. Understanding square roots helps in comprehending the structure of numbers and their properties. The concept of square roots extends beyond simple arithmetic, influencing fields such as algebra, geometry, and even real-life applications.
Throughout this guide, we have explored the definition, calculation, and properties of square roots. We also examined why the number 9 has two square roots and how these roots are used in different mathematical fields and real-life applications.
Visual representations and frequent questions further illustrate the practical and theoretical significance of square roots. By recognizing the positive and negative square roots, we appreciate the symmetry and balance inherent in mathematics.
Ultimately, the square roots of 9 exemplify the beauty and complexity of mathematical principles, encouraging deeper exploration and understanding.
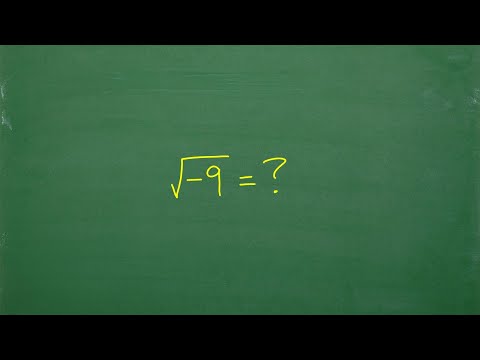
Video giải thích về căn bậc hai của số âm – 9, với cách tiếp cận chi tiết và dễ hiểu để thu hút người xem.
Căn bậc hai của – 9 là gì?
READ MORE:
Video giới thiệu về khái niệm căn bậc hai với cách giải thích dễ hiểu từ thầy J, thu hút người xem học toán.
Căn bậc hai là gì? | Toán học với thầy J