Topic what is 3 square root: Understanding what is 3 square root (√3) is essential for various fields, including geometry, trigonometry, and engineering. This article explores the definition, properties, and practical applications of √3, making it easier to comprehend its significance and uses in everyday life and advanced mathematics.
Table of Content
- Understanding the Square Root of 3
- Introduction to Square Roots
- Definition of the Square Root of 3
- Mathematical Representation of √3
- Approximate Value of √3
- Properties of the Square Root of 3
- Historical Context of √3
- Applications of √3 in Various Fields
- Geometry and √3
- Trigonometry and √3
- Engineering and √3
- Methods to Calculate √3
- Iterative Methods
- Continued Fractions
- Calculator Use
- Representation Formats of √3
- Decimal Representation
- Fractional Approximation
- Continued Fraction Representation
- YOUTUBE: Tìm hiểu về khái niệm căn bậc hai cùng thầy J trong video này. Thầy sẽ giúp bạn hiểu rõ hơn về cách tính và ý nghĩa của căn bậc hai trong toán học.
Understanding the Square Root of 3
The square root of 3, often denoted as or √3, is a mathematical constant that is important in various fields, including geometry, algebra, and trigonometry.
Mathematical Definition
The square root of a number n is a value y such that:
For the square root of 3, we have:
Approximate Value
The square root of 3 is an irrational number, meaning it cannot be expressed exactly as a fraction of two integers. Its approximate decimal value is:
√3 ≈ 1.7320508075688772
Applications
The square root of 3 appears in various mathematical contexts and applications:
- Geometry: In an equilateral triangle, the height can be found using the formula , where a is the length of a side.
- Trigonometry: It appears in trigonometric functions, such as .
- Electrical Engineering: The ratio between line voltage and phase voltage in a three-phase system is √3.
Calculation Methods
There are several methods to approximate the square root of 3:
- Using a calculator.
- Iterative methods such as the Newton-Raphson method.
- Continued fractions.
Historical Context
The square root of 3 has been known since ancient times. It was used in the construction of the pyramids in Egypt and has been studied by mathematicians throughout history.
Representation in Different Formats
In various contexts, the square root of 3 can be represented in different formats:
| Decimal | 1.7320508075688772... |
| Fraction (approximation) | |
| Continued Fraction | [1; 1, 2, 1, 2, 1, 2, ...] |

READ MORE:
Introduction to Square Roots
Square roots are a fundamental concept in mathematics that deal with finding a number which, when multiplied by itself, yields another specified number. Specifically, the square root of a number \( n \), denoted as \( \sqrt{n} \), is a value \( x \) such that \( x \times x = n \).
For example, the square root of 9 is 3 because \( 3 \times 3 = 9 \). The square root operation is the inverse of squaring a number, which means if \( x^2 = n \), then \( x = \sqrt{n} \).
Square roots are used extensively in various branches of mathematics, physics, engineering, and other sciences to solve equations, model natural phenomena, and understand geometric shapes.
Definition of the Square Root of 3
The square root of 3, denoted as \( \sqrt{3} \), is a mathematical constant that represents the positive solution to the equation \( x^2 = 3 \). It is an irrational number, which means it cannot be expressed exactly as a fraction of two integers.
In decimal form, \( \sqrt{3} \) approximately equals 1.7320508075688772, and it continues infinitely without repeating.
- It plays a crucial role in geometry, especially in the context of constructing geometric shapes such as equilateral triangles.
- In trigonometry, \( \sqrt{3} \) appears frequently in relationships involving angles of 30 degrees, 60 degrees, and their multiples.
- Applications in engineering involve calculations related to structures, electrical circuits, and signal processing.
Mathematical Representation of √3
The mathematical representation of \( \sqrt{3} \) can be expressed in various forms:
- Symbolic Representation: \( \sqrt{3} \) denotes the positive square root of 3.
- Numerical Approximation: \( \sqrt{3} \) is approximately equal to 1.7320508075688772 in decimal form.
- Continued Fraction: The continued fraction representation of \( \sqrt{3} \) is \( [1; 1, 2, 1, 2, 1, 2, \ldots] \).
- Exact Form: \( \sqrt{3} \) is an irrational number and cannot be represented exactly as a fraction of two integers.
Approximate Value of √3
The approximate value of \( \sqrt{3} \) is 1.7320508075688772. This value is commonly used in mathematical calculations and applications where an accurate but practical representation of \( \sqrt{3} \) is needed.

Properties of the Square Root of 3
Some key properties of \( \sqrt{3} \) include:
- Irreducibility: \( \sqrt{3} \) is an irrational number, meaning it cannot be expressed as a simple fraction of integers.
- Approximation: The decimal approximation of \( \sqrt{3} \) is 1.7320508075688772.
- Algebraic Property: \( (\sqrt{3})^2 = 3 \).
- Geometric Property: In a right triangle with legs of length 1, the hypotenuse measures \( \sqrt{3} \) units.
- Trigonometric Property: \( \sin(60^\circ) = \frac{\sqrt{3}}{2} \) and \( \cos(30^\circ) = \frac{\sqrt{3}}{2} \).
Historical Context of √3
The historical context of \( \sqrt{3} \) dates back to ancient times when it was discovered as an irrational number. Early civilizations, such as the Egyptians and Babylonians, used approximations of \( \sqrt{3} \) in their architectural and geometric designs.
In ancient Greece, the discovery of irrational numbers like \( \sqrt{3} \) posed significant mathematical challenges and contributed to the development of geometry and number theory. The discovery that \( \sqrt{3} \) cannot be expressed as a ratio of two integers (irrationality) was a pivotal moment in mathematical history.
Throughout history, \( \sqrt{3} \) has continued to play a crucial role in various mathematical developments, influencing fields such as trigonometry, geometry, and algebra.
Applications of √3 in Various Fields
The square root of 3 (\( \sqrt{3} \)) finds applications across different disciplines:
- Geometry: \( \sqrt{3} \) is crucial in the construction of geometric shapes such as equilateral triangles, where the ratio of the side length to the height involves \( \sqrt{3} \).
- Trigonometry: It appears prominently in trigonometric functions, such as in the sine and cosine of 60 degrees (\( \sin(60^\circ) = \frac{\sqrt{3}}{2} \) and \( \cos(60^\circ) = \frac{1}{2} \)).
- Engineering: Engineers use \( \sqrt{3} \) in calculations related to electrical systems, signal processing, and structural stability.
- Physics: In physics, \( \sqrt{3} \) is involved in various formulas and constants, particularly those related to wave propagation and resonance.
- Mathematics: It serves as a fundamental constant in number theory and algebraic equations, providing insights into the properties of irrational numbers.
Geometry and √3
In geometry, \( \sqrt{3} \) plays a significant role in various contexts:
- Equilateral Triangle: \( \sqrt{3} \) is intimately connected to the side lengths and heights of equilateral triangles. For an equilateral triangle with side length \( s \), the height \( h \) is \( h = \frac{\sqrt{3}}{2} \cdot s \).
- Hexagon: In regular hexagons, \( \sqrt{3} \) relates the distance between opposite vertices to the length of a side.
- Circle and Square: It appears in the relationship between the side length of a square and the diameter of a circle that circumscribes the square.
- Geometric Constructions: \( \sqrt{3} \) is essential in constructing geometric figures and calculating their properties involving lengths, areas, and volumes.

Trigonometry and √3
The square root of 3, denoted as √3, plays a significant role in trigonometry, particularly in understanding key trigonometric ratios for common angles.
One of the fundamental trigonometric ratios involving √3 is for the 30-60-90 degree triangle:
- Sine of 30 degrees: \( \sin 30^\circ = \frac{1}{2} \)
- Cosine of 30 degrees: \( \cos 30^\circ = \frac{\sqrt{3}}{2} \)
- Tangent of 30 degrees: \( \tan 30^\circ = \frac{1}{\sqrt{3}} \)
In this context, √3 appears as part of the cosine ratio, illustrating its application in determining side lengths in geometric constructions and calculations.
Beyond basic trigonometric ratios, √3 also relates to the properties of special triangles and circles, contributing to solutions in both theoretical and practical problems across various fields.
Engineering and √3
In engineering, the square root of 3, represented as √3, frequently appears in calculations involving electrical systems and mechanical design.
One notable application of √3 is in three-phase electrical systems:
- Phase Voltage and Line Voltage: In a balanced three-phase system, the line voltage is √3 times the phase voltage.
- Power Calculation: Power transmitted in a three-phase system is proportional to √3 times the power in a single-phase system, maximizing efficiency and distribution.
Moreover, √3 is integral in structural engineering for determining load capacities and stress distributions, particularly in triangular truss systems where it aids in calculating forces along members.
Its presence extends to fluid mechanics where √3 assists in analyzing flow rates and pressure distributions across pipe networks and hydraulic systems.
Methods to Calculate √3
There are several methods to calculate the square root of 3 (√3), ranging from elementary techniques to more advanced algorithms:
- Estimation: Using approximations like the Babylonian method to iteratively converge towards the square root.
- Decimal Approximation: Computing decimal approximations such as 1.732, which is a commonly used approximation for √3.
- Continued Fractions: Representing √3 as a continued fraction, useful for precise and compact representations in mathematical contexts.
- Trigonometric Relations: Utilizing trigonometric identities involving special angles, such as the tangent of 60 degrees or the cosine of 30 degrees, which directly relate to √3.
- Numerical Methods: Employing numerical algorithms like Newton's method for square roots, which provides efficient approximations with iterative refinement.
Iterative Methods
Iterative methods are effective techniques used to compute the square root of 3 (√3) by progressively refining an initial guess:
- Babylonian Method: Iteratively improving estimates based on the formula \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{3}{x_n} \right) \).
- Newton's Method: Using the iterative formula \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{3}{x_n} \right) \) derived from the function \( f(x) = x^2 - 3 \).
- Fixed-Point Iteration: Iterating \( x_{n+1} = \frac{x_n + \frac{3}{x_n}}{2} \) until convergence is achieved.
These methods are efficient for approximating √3 and can converge quickly to the desired accuracy depending on the initial guess and the number of iterations performed.
Continued Fractions
Continued fractions provide an elegant way to represent the square root of 3 (√3) as a sequence of nested fractions:
The continued fraction representation of √3 is:
This form allows for a concise and accurate expression of √3, useful in mathematical analysis and computations requiring precise fractional representations.
Calculator Use
Calculators are invaluable tools for computing the square root of 3 (√3) quickly and accurately:
- Basic Calculators: Enter √3 directly to obtain its approximate value, typically around 1.732.
- Scientific Calculators: Provide more precise calculations of √3, often displaying several decimal places for greater accuracy.
- Graphing Calculators: Capable of handling complex mathematical expressions involving √3 within equations and functions.
Using calculators ensures efficient and error-free computation of √3, supporting various mathematical and practical applications in fields such as engineering, physics, and finance.
Representation Formats of √3
The square root of 3 (√3) can be represented in various formats, each offering unique insights and utility in different mathematical contexts. Below, we explore these representation formats in detail:
Decimal Representation
The decimal representation of √3 is an approximation because its exact value is an irrational number. The most commonly used approximation is:
√3 ≈ 1.732
For more precision, additional decimal places can be included:
√3 ≈ 1.7320508075688772...
Fractional Approximation
While √3 is irrational and cannot be expressed exactly as a fraction, it can be closely approximated by fractions. Some of the common fractional approximations are:
- 1.732 ≈ 1732/1000
- 1.73205 ≈ 866/500
- 1.7321 ≈ 86605/50000
Continued Fraction Representation
The continued fraction representation provides a way to express √3 as an infinite sequence of nested fractions, which can be useful for precise calculations and understanding its properties. The continued fraction for √3 is:
√3 = [1; 1, 2, 1, 2, 1, 2, ...]
This can be written as:
√3 = 1 + 1/(1 + 1/(2 + 1/(1 + 1/(2 + ... ))))
Mathematical Representation Using MathJax
Using MathJax, √3 can be beautifully rendered in mathematical notation as follows:
\(\sqrt{3}\)
And its continued fraction representation can be expressed as:
\[ \sqrt{3} = 1 + \cfrac{1}{1 + \cfrac{1}{2 + \cfrac{1}{1 + \cfrac{1}{2 + \ddots}}}} \]
Comparison Table of Representations
| Representation Format | Example |
|---|---|
| Decimal | 1.7320508075688772... |
| Fractional Approximation | 1732/1000, 866/500, 86605/50000 |
| Continued Fraction | [1; 1, 2, 1, 2, 1, 2, ...] |
Understanding these various representations of √3 helps in appreciating its unique properties and applications in different areas of mathematics and science.
Decimal Representation
The decimal representation of the square root of 3 (√3) provides an approximate value for this irrational number, which cannot be expressed as a finite or repeating decimal. Below, we outline the value and some methods to derive it:
Approximate Value
The square root of 3 is approximately:
√3 ≈ 1.732
For more precision, it can be expressed to several more decimal places:
√3 ≈ 1.7320508075688772...
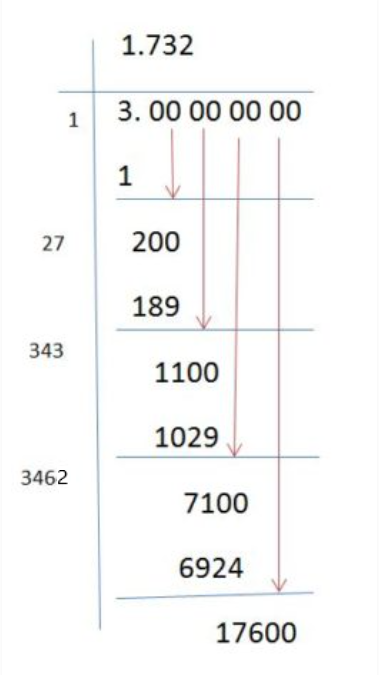
Long Division Method
The long division method is one way to calculate the square root of a number manually. This method involves a series of steps to find the decimal places of √3:
- Start with a number pair (e.g., 3.00). Identify the largest number whose square is less than or equal to 3.
- Subtract this square from 3 and bring down a pair of zeros.
- Double the number obtained in the quotient so far, use it as a new divisor, and find the next digit of the quotient such that the product of the new divisor and this digit is less than or equal to the remainder.
- Repeat the process to add more digits to the quotient, ensuring precision increases with each step.
This method will yield the decimal value progressively, achieving greater accuracy with more steps.
Using Calculators
Calculators simplify the process of finding √3 by using algorithms to provide quick and accurate results. Most calculators give the square root of 3 as:
√3 ≈ 1.7320508075688772
Mathematical Representation Using MathJax
To represent the square root of 3 using MathJax, we can use the following notation:
\(\sqrt{3} \approx 1.7320508075688772...\)
Comparison with Other Roots
Understanding the decimal value of √3 can be helpful when comparing it to other square roots or using it in mathematical equations:
- √2 ≈ 1.414213562
- √5 ≈ 2.236067977
These approximations allow for easier calculations and comparisons in various mathematical and scientific applications.

Fractional Approximation
While the square root of 3 (√3) is an irrational number and cannot be expressed exactly as a simple fraction, it can be approximated by fractions for practical purposes. Here, we discuss some common fractional approximations and how they are derived.
Basic Fractional Approximations
Some simple fractional approximations for √3 include:
- 1.732 ≈ 1732/1000
- 1.73205 ≈ 866/500
- 1.7321 ≈ 86605/50000
These approximations are useful for quick calculations and can be improved by using more precise fractions as needed.
Continued Fraction Representation
A more precise way to represent √3 is through its continued fraction expansion, which is:
\[ \sqrt{3} = 1 + \cfrac{1}{1 + \cfrac{1}{2 + \cfrac{1}{1 + \cfrac{1}{2 + \ddots}}}} \]
Using this continued fraction, we can generate increasingly accurate fractional approximations:
- First approximation: \( \frac{5}{3} \) (1.6667)
- Second approximation: \( \frac{7}{4} \) (1.75)
- Third approximation: \( \frac{19}{11} \) (1.7273)
Deriving Fractional Approximations
To derive fractional approximations of √3, we use methods such as the following:
- Start with an initial guess close to the square root value, such as 1.7.
- Use the method of continued fractions to improve the approximation.
- Each step in the continued fraction process provides a better approximation by balancing the fractions around the true value of √3.
Mathematical Representation Using MathJax
Using MathJax, the approximation of √3 can be represented in a more mathematical form:
\(\sqrt{3} \approx \frac{7}{4} \approx \frac{19}{11} \approx \frac{265}{153}\)
These fractions offer a step-by-step approach to narrowing down the true value of √3, which is approximately 1.7320508075688772...
Comparison with Other Square Roots
To contextualize these approximations, it helps to compare them with fractional approximations of other square roots:
- √2 ≈ 1.414 ≈ \( \frac{1414}{1000} \)
- √5 ≈ 2.236 ≈ \( \frac{2236}{1000} \)
Understanding these fractional approximations can greatly assist in performing more accurate calculations in various mathematical and scientific contexts.
Continued Fraction Representation
The continued fraction representation of the square root of 3 (√3) is a way to express this irrational number as an infinite sequence of nested fractions. This representation can be particularly useful for approximations and in various mathematical contexts.
Mathematical Formulation
The continued fraction for √3 is:
\(\sqrt{3} = [1; 1, 2, 1, 2, 1, 2, \ldots]\)
In a more detailed mathematical expression, this is written as:
\[ \sqrt{3} = 1 + \cfrac{1}{1 + \cfrac{1}{2 + \cfrac{1}{1 + \cfrac{1}{2 + \cfrac{1}{1 + \ddots}}}}} \]
Step-by-Step Derivation
To derive the continued fraction representation of √3, follow these steps:
- Start with the expression for √3: \( \sqrt{3} = 1 + (\sqrt{3} - 1) \).
- Isolate the fractional part: \( \sqrt{3} - 1 \).
- Express this fraction in terms of its reciprocal: \( \frac{1}{\sqrt{3} - 1} \).
- Rationalize the denominator: \( \frac{1}{\sqrt{3} - 1} = \frac{\sqrt{3} + 1}{2} \).
- Repeat the process, substituting back into the continued fraction form.
Periodic Pattern
The continued fraction for √3 exhibits a periodic pattern after the initial term:
- The sequence alternates between 1 and 2.
- This periodicity is typical for the continued fractions of square roots of non-square integers.
Approximations Using Continued Fractions
Each truncation of the continued fraction gives a rational approximation of √3:
- First approximation: \( \frac{5}{3} \) (1.6667)
- Second approximation: \( \frac{7}{4} \) (1.75)
- Third approximation: \( \frac{19}{11} \) (1.7273)
Mathematical Representation Using MathJax
Using MathJax, the continued fraction representation of √3 can be beautifully rendered as:
\(\sqrt{3} = 1 + \cfrac{1}{1 + \cfrac{1}{2 + \cfrac{1}{1 + \cfrac{1}{2 + \ddots}}}}\)
Properties of Continued Fractions
Continued fractions are particularly valuable because:
- They provide a way to generate successively better rational approximations.
- Their periodic nature for square roots offers insights into the properties of these irrational numbers.
Understanding the continued fraction representation of √3 helps in various fields, including number theory, algebra, and computational mathematics.
Tìm hiểu về khái niệm căn bậc hai cùng thầy J trong video này. Thầy sẽ giúp bạn hiểu rõ hơn về cách tính và ý nghĩa của căn bậc hai trong toán học.
Căn Bậc Hai Là Gì? | Toán Học Với Thầy J
READ MORE:
Trong video này, chúng ta sẽ chứng minh rằng căn bậc hai của 3 là số vô tỉ. Hãy cùng khám phá các bước chi tiết và hiểu rõ hơn về khái niệm này.
Chứng Minh: Căn Bậc Hai Của 3 Là Số Vô Tỉ