Topic y square root: The concept of the square root is fundamental in mathematics, and understanding the square root of \( y \) opens the door to solving a myriad of problems in algebra, geometry, and beyond. Dive into this comprehensive guide to explore the intricacies of square roots, their applications, and why they are essential in various fields of study.
Table of Content
- The Concept of Square Roots
- Introduction to Square Roots
- Mathematical Definition of Square Roots
- Positive and Negative Square Roots
- Square Roots of Perfect Squares
- Square Roots of Non-Perfect Squares
- Imaginary and Complex Numbers in Square Roots
- Methods to Calculate Square Roots
- Using Estimation and Approximation
- Square Roots in Geometry
- Applications in Physics and Engineering
- Square Roots in Finance and Economics
- Common Square Root Values and Their Uses
- Graphing Square Root Functions
- Challenges and Common Mistakes with Square Roots
- Square Roots in Algebraic Equations
- Advanced Square Root Concepts
- Historical Perspective on Square Roots
- Conclusion and Summary
- YOUTUBE: Hướng dẫn cách vẽ đồ thị hàm số căn bậc hai qua các phép biến đổi và vẽ điểm. Video hữu ích cho những ai đang học toán và muốn hiểu rõ hơn về hàm số căn bậc hai.
The Concept of Square Roots
The square root of a number \( y \) is a value that, when multiplied by itself, gives \( y \). Mathematically, this is expressed as:
Here, the square root of \( y \) is denoted as \( \sqrt{y} \), where:
Properties of Square Roots
- For any non-negative number \( y \), there are two square roots: \( \sqrt{y} \) and \( -\sqrt{y} \). For example, both 4 and -4 are square roots of 16.
- The square root of 0 is 0.
- For any positive number \( y \), \( \sqrt{y} \) is always positive.
- Square roots of negative numbers are not real numbers but are called imaginary numbers. These are expressed using the imaginary unit \( i \), where \( i = \sqrt{-1} \).
Examples
Consider the following examples of square roots:
| Number ( \( y \) ) | Square Root ( \( \sqrt{y} \) ) |
|---|---|
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
| -1 | \( i \) |
Applications of Square Roots
Square roots have various applications in real-life and mathematics, including:
- Geometry: Calculating the side length of a square given its area.
- Physics: Determining root mean square values in waveforms and signal processing.
- Finance: Computing the volatility of returns in financial markets using the standard deviation.
READ MORE:
Introduction to Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. It is a fundamental concept in mathematics, essential for various applications in science, engineering, and finance. The square root symbol is represented as √, and the square root of a number x is written as √x.
For example:
- √4 = 2 because 2 × 2 = 4
- √9 = 3 because 3 × 3 = 9
Square roots can be categorized into two main types:
- Perfect Square Roots: These are square roots of perfect squares (numbers like 4, 9, 16) that result in whole numbers.
- Non-Perfect Square Roots: These are square roots of non-perfect squares (numbers like 2, 3, 5) that result in irrational numbers.
Mathematically, if y = √x, then y2 = x. This can also be written using the exponent form as x1/2.
Here are a few properties of square roots:
- Every positive number has two square roots: one positive (principal square root) and one negative.
- The square root of zero is zero.
- Square roots of negative numbers are imaginary, involving the imaginary unit i where i2 = -1.
Let's consider the function for square roots:
If f(x) = √x, then:
- f(4) = 2
- f(9) = 3
- f(0) = 0
In graphical terms, the function y = √x represents a curve that starts at the origin (0,0) and increases slowly, reflecting the property that as x increases, the value of √x also increases but at a decreasing rate.
Understanding square roots is crucial for solving quadratic equations, analyzing functions, and exploring advanced mathematical concepts. This guide will delve deeper into these aspects, providing comprehensive knowledge and practical applications of square roots.
Mathematical Definition of Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. It is represented by the radical symbol √. For example, the square root of 9 is 3, because \(3 \times 3 = 9\).
Mathematically, if \(y\) is the square root of \(x\), then:
\[
y = \sqrt{x} \quad \text{such that} \quad y^2 = x
\]
Some key properties of square roots include:
- The square root of a product is the product of the square roots: \[ \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \] This property holds true for non-negative values of \(a\) and \(b\).
- The square root of a quotient is the quotient of the square roots: \[ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \] provided \(b \neq 0\).
- The square root function is defined for non-negative numbers. For negative numbers, square roots involve imaginary numbers, denoted by \(i\), where \(i = \sqrt{-1}\).
To illustrate, consider the square root of 36:
\[
\sqrt{36} = 6 \quad \text{since} \quad 6^2 = 36
\]
There are two square roots for every positive number: a positive and a negative root. For instance:
\[
\sqrt{25} = 5 \quad \text{and} \quad -\sqrt{25} = -5
\]
This is often represented as:
\[
\pm \sqrt{x}
\]
Square roots play a crucial role in various mathematical operations and have numerous applications in different fields, including geometry, physics, and finance.
Positive and Negative Square Roots
Square roots are mathematical operations that determine a number which, when multiplied by itself, results in the given number. Every positive number \( x \) has two square roots: one positive and one negative.
The principal square root of a number \( x \) is denoted as \( \sqrt{x} \) and is always non-negative. The negative square root is denoted as \( -\sqrt{x} \). Together, they can be represented as \( \pm \sqrt{x} \).
For example:
- The square roots of 25 are \( \sqrt{25} = 5 \) and \( -\sqrt{25} = -5 \), since \( 5^2 = 25 \) and \( (-5)^2 = 25 \).
- For the number 81, the square roots are \( \sqrt{81} = 9 \) and \( -\sqrt{81} = -9 \).
The absolute value notation helps in defining the principal square root, ensuring the result is non-negative:
- \(\sqrt{(x-2)^2} = |x-2|\)
Zero is unique in that it has only one square root:
- \(\sqrt{0} = 0\)
In the context of the quadratic formula, the positive and negative roots are represented explicitly:
- \(x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\)
Understanding that every positive real number has two square roots helps in solving various mathematical problems, particularly in algebra and calculus.
Square Roots of Perfect Squares
Perfect squares are numbers that are the product of an integer multiplied by itself. For example, \( 1 \times 1 = 1 \), \( 2 \times 2 = 4 \), \( 3 \times 3 = 9 \), and so on. These numbers are called perfect squares because their square roots are whole numbers.
Here are some properties of perfect squares:
- The square root of a perfect square is always an integer.
- Perfect squares are always non-negative, since both positive and negative numbers when squared result in a positive product.
- The units digit of a perfect square can only be 0, 1, 4, 5, 6, or 9.
Examples of perfect squares:
| Integer | Perfect Square |
|---|---|
| 1 | \(1^2 = 1\) |
| 2 | \(2^2 = 4\) |
| 3 | \(3^2 = 9\) |
| 4 | \(4^2 = 16\) |
| 5 | \(5^2 = 25\) |
| 6 | \(6^2 = 36\) |
| 7 | \(7^2 = 49\) |
| 8 | \(8^2 = 64\) |
| 9 | \(9^2 = 81\) |
| 10 | \(10^2 = 100\) |
To determine if a number is a perfect square, you can calculate its square root and check if the result is a whole number. For instance, \(\sqrt{49} = 7\), which is a whole number, so 49 is a perfect square. However, \(\sqrt{50} \approx 7.07\), which is not a whole number, so 50 is not a perfect square.
Understanding perfect squares is fundamental in mathematics as it helps in simplifying expressions and solving quadratic equations.

Square Roots of Non-Perfect Squares
The square root of a non-perfect square is an irrational number, meaning it cannot be exactly represented as a simple fraction and its decimal form goes on infinitely without repeating. Calculating these square roots involves approximation methods. Here are some detailed steps and methods for approximating square roots of non-perfect squares:
Approximation by Nearest Perfect Squares
To estimate the square root of a non-perfect square, you can use the nearest perfect squares. For example, to approximate the square root of 90:
- Identify the nearest perfect squares around 90, which are 81 (92) and 100 (102).
- Since 90 is between 81 and 100, the square root of 90 will be between 9 and 10.
- Estimate by narrowing down: 90 is closer to 100, so guess around 9.4 or 9.5.
- Refine the estimate using a fractional approach. For example, 90 is 9 units above 81 and 19 units below 100, thus we get a fraction 9/19. Adding this fraction to the lower bound, 9 + (9/19), gives a closer estimate.
- Using this method, you get approximately 9.47, which can be verified and refined further using a calculator.
Using Number Line for Visual Approximation
Another way to approximate square roots is by using a number line:
- Plot the non-perfect square number on a number line between its nearest perfect squares.
- Visually determine the position of the number. For example, the square root of 90 is slightly less than halfway between 9 and 10, closer to 9.5.
- Refine this visual estimate to get a more accurate value.
Decimal Approximations
For more precision, decimal approximations can be used:
- Start with a rough estimate, then square the estimate to see how close it is to the original number.
- If the estimate squared is too high, lower the estimate; if too low, increase it.
- Repeat this process, increasing the decimal places as needed until the desired accuracy is reached.
Example
To find the square root of 2.5:
- Recognize that 2.5 is between 1 and 4, so its square root is between 1 and 2.
- Estimate halfway between 1 and 2, which is 1.5, and refine: 1.52 = 2.25 (too low).
- Try 1.6: 1.62 = 2.56 (too high).
- Therefore, the square root of 2.5 is approximately 1.6.
Conclusion
While exact values for the square roots of non-perfect squares are challenging to determine without a calculator, these methods provide practical ways to estimate and understand these values. Continuous practice with these techniques can improve accuracy and understanding.
Imaginary and Complex Numbers in Square Roots
In mathematics, square roots are not limited to real numbers; they extend into the realm of imaginary and complex numbers. This extension allows for a comprehensive understanding and application of square roots beyond the limitations of the real number system.
Complex numbers are numbers that have both a real part and an imaginary part. A complex number is expressed in the form \( a + bi \), where \( a \) and \( b \) are real numbers, and \( i \) is the imaginary unit defined by the property \( i^2 = -1 \). This imaginary unit \( i \) enables the definition of square roots of negative numbers, which are not possible within the real numbers.
- The square root of a negative number can be expressed using \( i \). For example:
- \(\sqrt{-4} = \sqrt{4 \cdot -1} = 2i\)
- \(\sqrt{-9} = \sqrt{9 \cdot -1} = 3i\)
- Every complex number \( a + bi \) has a corresponding conjugate \( a - bi \). The product of a complex number and its conjugate is always a non-negative real number:
- \((a + bi)(a - bi) = a^2 + b^2\)
- The magnitude or modulus of a complex number \( a + bi \) is given by:
- \(|a + bi| = \sqrt{a^2 + b^2}\)
- Complex numbers can be represented graphically on the complex plane, where the x-axis represents the real part and the y-axis represents the imaginary part.
Complex numbers play a crucial role in various fields such as engineering, physics, and applied mathematics, providing a robust framework for solving equations that have no real solutions. For example, the equation \( x^2 + 1 = 0 \) has no real solutions, but it has two complex solutions: \( x = i \) and \( x = -i \).
Methods to Calculate Square Roots
Calculating square roots can be done through various methods, each with its own level of precision and computational complexity. Here, we will explore several methods, including both manual and algorithmic approaches.
-
Prime Factorization:
This method works best for perfect squares. It involves finding the prime factors of the number and then pairing them.
- Factorize the number into its prime factors.
- Pair the prime factors.
- Take one number from each pair and multiply them together to get the square root.
For example, to find the square root of 36:
\[ 36 = 2^2 \times 3^2 \]
\[ \sqrt{36} = 2 \times 3 = 6 \]
-
Long Division Method:
This method is similar to the long division process and is effective for both perfect and non-perfect squares.
- Group the digits in pairs, starting from the decimal point.
- Find the largest number whose square is less than or equal to the first group.
- Subtract the square from the first group and bring down the next pair of digits.
- Double the quotient, place it as the new divisor, and find the digit that fits the division.
- Repeat the process for the desired number of decimal places.
-
Babylonian (Heron's) Method:
This is an iterative algorithm that provides a good approximation of the square root.
- Start with an initial guess \( x_0 \) (a rough estimate).
- Use the formula: \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{S}{x_n} \right) \).
- Repeat the iteration until the difference between \( x_n \) and \( x_{n+1} \) is less than a predefined threshold.
For example, to find the square root of 10:
Let the initial guess be \( x_0 = 3 \):
\[ x_1 = \frac{1}{2} \left( 3 + \frac{10}{3} \right) \approx 3.1667 \]
Continue iterating to refine the approximation.
-
Using a Calculator:
Most calculators have a square root function, which provides a quick and accurate result. Simply enter the number and press the square root button.
-
Newton's Method:
Similar to the Babylonian method, Newton's method can also be used to find square roots by iterative approximation.
- Choose an initial guess \( x_0 \).
- Apply the iteration formula: \( x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} \), where \( f(x) = x^2 - S \).
- Repeat until convergence.
Each of these methods has its advantages and is suitable for different types of problems. For practical purposes, using a calculator or a computer algorithm is often the most efficient way to find square roots.
Using Estimation and Approximation
Calculating square roots using estimation and approximation methods is essential for quickly finding approximate values without complex calculations. Here are some common methods:
- Method 1: Identifying Perfect Squares
To approximate the square root of a number \(n\), first identify the perfect squares closest to \(n\). For example, to find \(\sqrt{50}\):- Find the nearest perfect squares: \(49\) (which is \(7^2\)) and \(64\) (which is \(8^2\)).
- Since \(50\) is closer to \(49\), \(\sqrt{50} \approx 7\).
- For better precision, note that \(50\) is closer to \(49\) than to \(64\), so \(\sqrt{50} \approx 7.1\).
- Method 2: Average Method
This method involves taking the average of the square roots of the perfect squares around \(n\). For example, to estimate \(\sqrt{10}\):- Identify perfect squares: \(9\) (which is \(3^2\)) and \(16\) (which is \(4^2\)).
- Take the average: \(\frac{3 + 4}{2} = 3.5\).
- Check and refine: \(3.5^2 = 12.25\), so the approximation can be adjusted. \(\sqrt{10} \approx 3.16\).
- Method 3: Using the Binomial Series
For numbers close to a known perfect square, use the binomial series expansion. For example, for \(\sqrt{2}\):- Express \(\sqrt{2}\) as \(\sqrt{1 + 1}\).
- Use the binomial expansion: \(\sqrt{1 + 1} \approx 1 + \frac{1}{2} - \frac{1}{8} = 1.375\).
- Refine for better accuracy: \(\sqrt{2} \approx 1.414\).
- Method 4: Newton's Method
This iterative method starts with an initial guess and improves the approximation:- For \(\sqrt{N}\), let \(x_0\) be an initial guess.
- Iteratively apply: \(x_{n+1} = \frac{1}{2} \left( x_n + \frac{N}{x_n} \right)\).
- Example: For \(\sqrt{10}\) with \(x_0 = 3\):
- \(x_1 = \frac{1}{2} \left( 3 + \frac{10}{3} \right) = 3.1667\)
- \(x_2 = \frac{1}{2} \left( 3.1667 + \frac{10}{3.1667} \right) = 3.1623\)
- Continue until desired accuracy is reached.

Square Roots in Geometry
In geometry, square roots often appear in various contexts, particularly in relation to the dimensions of geometric shapes and their properties. Here are several key applications:
- Area of a Square: The side length \( s \) of a square is related to its area \( A \) by the formula \( A = s^2 \). To find the side length \( s \), one must take the square root of \( A \), giving \( s = \sqrt{A} \).
- Diagonal of a Square: If you know the side length \( s \) of a square, you can calculate the length of its diagonal \( d \) using \( d = s \sqrt{2} \). Here, \( \sqrt{2} \) represents the square root of 2, a fundamental constant in geometry.
- Right Triangle: In a right triangle with legs \( a \) and \( b \), the length of the hypotenuse \( c \) can be found using the Pythagorean theorem: \( c = \sqrt{a^2 + b^2} \).
- Circle: The radius \( r \) of a circle is related to its area \( A \) by \( A = \pi r^2 \). Solving for \( r \), we get \( r = \sqrt{\frac{A}{\pi}} \).
- Volume of a Cube: The volume \( V \) of a cube with side length \( s \) is \( V = s^3 \). To find \( s \), take the cube root of \( V \), giving \( s = \sqrt[3]{V} \).
Understanding these applications of square roots in geometry is crucial for solving various problems involving geometric shapes and their dimensions.
Applications in Physics and Engineering
Square roots play essential roles in various applications within the fields of physics and engineering. Here are some key uses:
- Mechanics: In mechanics, particularly in problems involving motion and acceleration, square roots are used to calculate velocities and accelerations from kinetic energy and momentum equations.
- Electrical Engineering: Square roots are fundamental in electrical engineering for calculating values such as RMS (Root Mean Square) voltage and current, which are crucial in designing circuits and analyzing electrical power.
- Signal Processing: In signal processing, square roots are used to determine the amplitude of signals, particularly in analyzing waveforms and digital signal processing algorithms.
- Structural Engineering: Square roots are applied in structural engineering to calculate stresses, strains, and load distributions within materials and components, aiding in the design and analysis of buildings, bridges, and other structures.
- Fluid Dynamics: In fluid dynamics, square roots are utilized in equations describing flow rates, pressure differentials, and turbulence, providing insights into fluid behavior and optimizing designs in hydraulic systems.
The versatility of square roots in physics and engineering underscores their importance in solving complex problems and advancing technological innovations.
Square Roots in Finance and Economics
In finance and economics, square roots are utilized in various calculations and models to analyze data and make informed decisions. Here are several key applications:
- Variance and Standard Deviation: Square roots are used to calculate the standard deviation, a measure of volatility or risk in financial markets. It provides insights into the variability of returns on investments.
- Portfolio Theory: Square roots play a role in portfolio theory, where they are used to calculate the volatility of a portfolio of assets, helping investors manage risk and optimize asset allocation.
- Option Pricing Models: In option pricing models like the Black-Scholes model, square roots are essential in formulas to calculate the volatility of the underlying asset, which influences the price of options.
- Interest Rate Modeling: Square roots are employed in interest rate modeling, such as in the calculation of the volatility of interest rates or in models like the Cox-Ingersoll-Ross model used to describe interest rate movements over time.
- Economic Growth and Forecasting: In economics, square roots are used in growth models to analyze factors such as GDP growth rates and population growth, providing insights into economic stability and future trends.
Understanding the role of square roots in finance and economics is crucial for making informed financial decisions, managing risk, and developing economic policies.
Common Square Root Values and Their Uses
Understanding common square root values is important across various disciplines due to their frequent appearance in calculations and practical applications. Here are some notable examples:
| Square Root | Numerical Value | Common Uses |
| \( \sqrt{2} \) | 1.414 | Used in geometry for the diagonal of a square, and in engineering for calculations involving proportions and ratios. |
| \( \sqrt{3} \) | 1.732 | Applied in geometry for calculations involving regular polygons and in physics for energy transfer calculations. |
| \( \sqrt{5} \) | 2.236 | Utilized in architecture and engineering for proportions and dimensions, and in finance for risk calculations. |
| \( \sqrt{10} \) | 3.162 | Commonly used in finance for risk assessment and portfolio management. |
These values are foundational in various fields, contributing to both theoretical understanding and practical applications across disciplines.
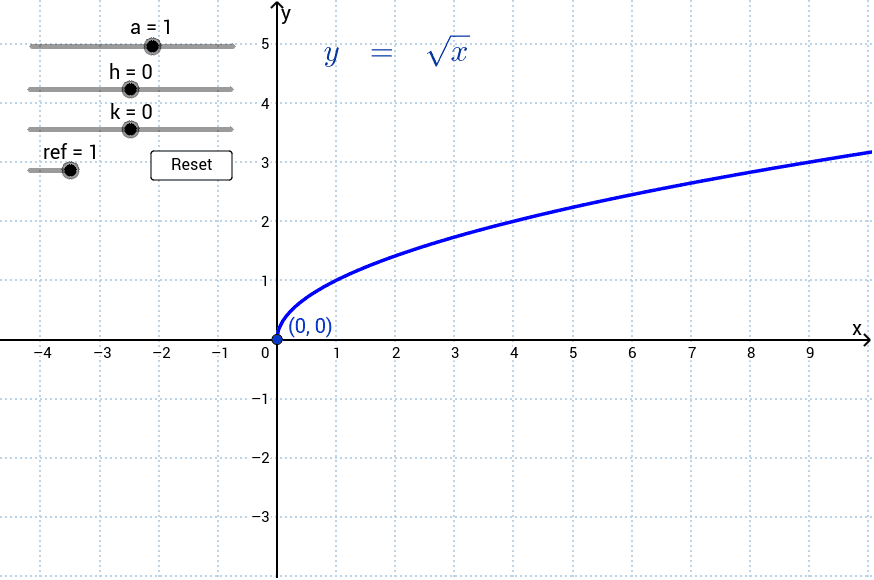
Graphing Square Root Functions
Graphing square root functions involves understanding their basic characteristics and how changes in parameters affect their shapes. Here's a step-by-step approach to graphing \( y = \sqrt{x} \):
- Identify the Domain: The square root function \( y = \sqrt{x} \) is defined for \( x \geq 0 \), as the square root of a negative number is not real.
- Plot Key Points: Choose values of \( x \) and calculate \( y = \sqrt{x} \). For example, \( (\sqrt{0}, 0), (\sqrt{1}, 1), (\sqrt{4}, 2), (\sqrt{9}, 3) \).
- Sketch the Graph: Connect the plotted points smoothly, noting the curve starts at the origin (0,0) and moves upwards as \( x \) increases.
- Consider Transformations: The general form \( y = a\sqrt{bx - h} + k \) involves shifts and stretches of the basic function. Adjust parameters \( a, b, h, \) and \( k \) accordingly.
- Understand Asymptotes: The graph approaches the y-axis but does not touch it, indicating a vertical asymptote at \( x = 0 \).
Graphing square root functions is fundamental in mathematics and serves as a basis for understanding more complex functions and their graphical representations.
Challenges and Common Mistakes with Square Roots
Working with square roots presents several challenges and common mistakes that are important to recognize and avoid. Here are some key considerations:
- Undefined Results: Square roots of negative numbers are not real numbers, leading to undefined results in real number calculations.
- Complex Numbers: Introducing complex numbers is essential when dealing with square roots of negative numbers, requiring careful handling to ensure accurate solutions.
- Extraneous Solutions: In equations involving square roots, solutions may include extraneous roots that do not satisfy the original equation, necessitating verification of solutions.
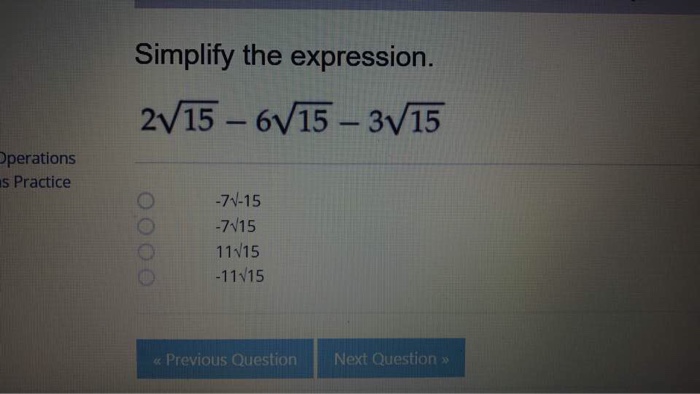
- Incorrect Simplification: Incorrectly simplifying expressions involving square roots can lead to errors in calculations, particularly in algebraic manipulations.
- Numerical Precision: Achieving precise numerical results with square roots requires attention to rounding errors and computational limitations, especially in practical applications.
Awareness of these challenges and mistakes helps improve accuracy and efficiency when working with square roots in various mathematical contexts.
Square Roots in Algebraic Equations
Square roots play a significant role in algebraic equations, offering solutions to various types of equations. Here's how square roots are utilized in algebra:
- Quadratic Equations: The solutions to quadratic equations of the form \( ax^2 + bx + c = 0 \) often involve square roots, given by the quadratic formula \( x = \frac{{-b \pm \sqrt{b^2 - 4ac}}}{{2a}} \).
- Radical Equations: Equations where the variable is under a square root, such as \( \sqrt{x} = a \), are solved by squaring both sides and careful consideration of domain restrictions.
- Complex Solutions: In equations involving complex numbers, square roots of negative values can lead to complex solutions, requiring consideration of both real and imaginary components.
- Systems of Equations: Square roots can be part of systems of equations where one equation involves squares or square roots, often requiring substitution or elimination methods for solving.
- Applications in Geometry: Geometric problems often translate into algebraic equations involving square roots, such as finding side lengths or areas of shapes based on given conditions.
Understanding how to manipulate and solve algebraic equations involving square roots is essential for both theoretical mathematics and practical applications across various fields.
Advanced Square Root Concepts
Advanced square root concepts delve into more intricate mathematical applications and theoretical constructs. Here are some advanced topics related to square roots:
- Nth Roots: Generalizing square roots to nth roots (\( \sqrt[n]{x} \)) involves understanding roots beyond just squares, extending to cubes, fourth roots, and so on.
- Complex Analysis: In complex analysis, square roots of complex numbers involve the concept of branch cuts and branch points, which affect the multi-valued nature of these functions.
- Matrix Square Roots: In linear algebra, finding square roots of matrices (if they exist) involves complex computations and has applications in solving systems of linear equations and in physics.
- Functional Square Roots: In functional analysis, square roots of operators and functions introduce concepts like spectral theory and functional calculus, which are crucial in advanced mathematical theories.
- Applications in Number Theory: Square roots are fundamental in number theory, where they are used in Diophantine equations, continued fractions, and the study of irrational numbers.
Exploring these advanced square root concepts enriches understanding across various mathematical disciplines, paving the way for deeper insights and applications in mathematics and related fields.

Historical Perspective on Square Roots
The study of square roots dates back to ancient civilizations, where they played significant roles in mathematics, astronomy, and engineering. Here's a historical journey through the development and significance of square roots:
- Ancient Babylonians: Babylonian mathematicians around 2000 BC used geometric methods to approximate square roots, laying foundational principles that later civilizations built upon.
- Ancient Egyptians: Egyptians utilized square roots in construction and land surveying, particularly in the design and layout of pyramids and other structures.
- Ancient Greeks: Greek mathematicians, such as Pythagoras and Euclid, formalized geometric principles involving squares and square roots, contributing to the development of algebraic methods.
- Islamic Scholars: During the Islamic Golden Age, scholars like Al-Khwarizmi and Al-Biruni made significant advancements in algebra, including solving quadratic equations and understanding the properties of square roots.
- Renaissance Europe: Mathematicians in Renaissance Europe, such as Fibonacci and Tartaglia, expanded on earlier works, refining methods for solving cubic and higher-order equations, often involving square roots.
- Modern Mathematics: In the modern era, developments in calculus, complex analysis, and number theory have deepened our understanding of square roots, leading to applications in physics, engineering, and computer science.
Throughout history, the study of square roots has evolved from practical applications in measurement and construction to foundational principles in mathematics, reflecting humanity's ongoing quest for understanding and knowledge.
Conclusion and Summary
Square roots are fundamental mathematical entities with diverse applications across various disciplines. Throughout this comprehensive guide, we explored:
- The basic definition and properties of square roots, including their calculation and representation.
- Practical applications in geometry, physics, engineering, finance, and economics.
- Common values of square roots and their specific uses in real-world scenarios.
- Graphical representations and advanced concepts such as nth roots, complex analysis, and matrix operations.
- A historical perspective on the development of square root concepts and their evolution over time.
Understanding square roots is crucial for problem-solving, critical thinking, and advancing scientific and technological innovations. Whether used in algebraic equations, geometric calculations, or financial models, square roots continue to play a central role in mathematics and its applications.
Hướng dẫn cách vẽ đồ thị hàm số căn bậc hai qua các phép biến đổi và vẽ điểm. Video hữu ích cho những ai đang học toán và muốn hiểu rõ hơn về hàm số căn bậc hai.
Vẽ đồ thị hàm số căn bậc hai bằng cách sử dụng phép biến đổi và vẽ điểm
READ MORE:
Hướng dẫn cách vẽ đồ thị phương trình căn bậc hai một cách chi tiết và dễ hiểu. Phù hợp cho người học toán và muốn nắm vững về hàm số căn bậc hai.
Cách vẽ đồ thị phương trình căn bậc hai