Square Root of 5 Rational or Irrational: A Mathematical Exploration

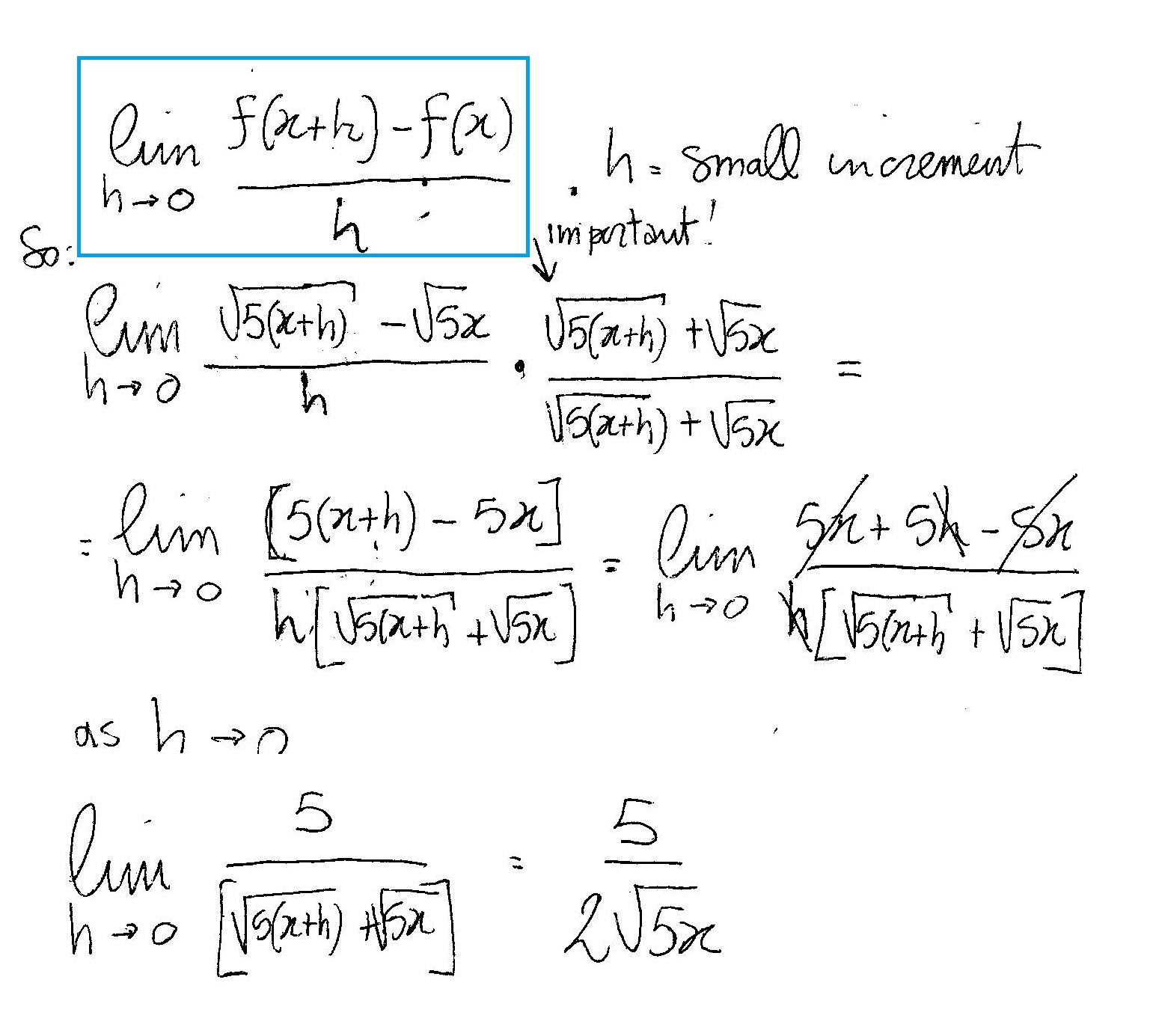
The square root of 5, denoted as \( \sqrt{5} \), is an irrational number. This means it cannot be expressed as a fraction \( \frac{p}{q} \), where \( p \) and \( q \) are integers and \( q \neq 0 \).

Proof by Contradiction

One common method to prove that \( \sqrt{5} \) is irrational is by contradiction. Here’s a sketch of the proof:

1. Assume \( \sqrt{5} = \frac{p}{q} \) for some integers \( p \) and \( q \) with no common factors.
2. Then \( 5 = \frac{p^2}{q^2} \), which implies \( 5q^2 = p^2 \).
3. Therefore, \( p^2 \) is divisible by 5, so \( p \) must also be divisible by 5. Let \( p = 5k \) for some integer \( k \).
4. Substituting back, \( 5q^2 = (5k)^2 \) gives \( 5q^2 = 25k^2 \) or \( q^2 = 5k^2 \).
5. This implies \( q^2 \) is divisible by 5, so \( q \) must also be divisible by 5.
6. This contradicts the assumption that \( p \) and \( q \) have no common factors other than 1.

Therefore, \( \sqrt{5} \) cannot be expressed as a fraction, proving it is irrational.

Long Division Method

Another method to demonstrate the irrationality of \( \sqrt{5} \) is using long division to show it has a non-terminating, non-repeating decimal expansion:

By performing long division, we find:

\( \sqrt{5} = 2.23606797749979 \ldots \)

This decimal continues infinitely without repeating, confirming that \( \sqrt{5} \) is irrational.

Geometric Interpretation

Geometrically, \( \sqrt{5} \) can be represented as the diagonal of a rectangle with sides of length 1 and 2 units. Using the Pythagorean theorem, the length of the diagonal \( d \) is:

\[
d = \sqrt{1^2 + 2^2} = \sqrt{1 + 4} = \sqrt{5}
\]

Conclusion

All these methods conclusively show that the square root of 5 is an irrational number.

The square root of 5, denoted as √5, is an important mathematical constant. This article explores whether √5 is rational or irrational, provides methods for calculating it, and discusses its significance in various mathematical contexts. We will also demonstrate how to represent √5 on a number line and prove its irrationality using different approaches.

The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 25 is 5, because \(5 \times 5 = 25\). This concept is fundamental in mathematics and is denoted using the radical sign, such as \(\sqrt{n}\) for the square root of \(n\).

Mathematically, if \( q \) is the square root of \( n \), it can be expressed as:
\[
q = \sqrt{n}
\]
or equivalently,
\[
q^2 = n
\]

To find the square root of a number, one can use various methods such as prime factorization, long division, or a calculator. For instance, the square root of 5 can be approximated as 2.2361 using a calculator. However, it is important to note that not all numbers have a neat, whole number as their square root.

Numbers that have whole number square roots are called perfect squares. Examples include 1, 4, 9, 16, and 25. However, the square root of 5 is not a whole number and thus, 5 is not a perfect square.

The distinction between rational and irrational numbers is also crucial when discussing square roots. A rational number can be expressed as a fraction of two integers, while an irrational number cannot. Since the square root of 5 cannot be expressed as an exact fraction, it is classified as an irrational number. The decimal representation of \(\sqrt{5}\) is non-terminating and non-repeating, further confirming its irrationality.

Understanding the properties and calculations of square roots is essential for various applications in mathematics, science, and engineering. The study of irrational numbers like \(\sqrt{5}\) opens up deeper insights into the nature of numbers and their classifications.

The square root of 5, denoted as √5, is an irrational number. This means that it cannot be expressed as a simple fraction or a ratio of two integers. Instead, it is represented by an infinite non-repeating decimal. The approximate value of √5 is 2.23606797749979...

In mathematical notation, the square root of 5 is written as:

\[\sqrt{5}\]

To better understand the mathematical representation of √5, consider the following points:

• The square root of a number \( x \) is a value \( y \) such that \( y^2 = x \). In this case, we need to find \( y \) such that \( y^2 = 5 \).
• Since 5 is not a perfect square, √5 is not a whole number.
• Using the quadratic formula, we can confirm that there are no rational solutions to \( x^2 - 5 = 0 \), hence √5 is irrational.

In decimal form, the representation of √5 is non-terminating and non-repeating, which is one of the key characteristics of irrational numbers:

\[ \sqrt{5} \approx 2.23606797749979... \]

For practical purposes, √5 can be approximated using various methods:

1. Using a calculator: Most scientific calculators have a square root function that provides an approximate decimal value of √5.
2. Using a computer: Software such as Python or MATLAB can compute √5 to a high degree of precision.
3. Manual calculation: Methods such as the Babylonian method (also known as Heron's method) can be used to iteratively approximate the value of √5.

Understanding the representation of √5 is essential in various fields such as geometry, algebra, and number theory, where the concept of irrational numbers plays a crucial role.

No, 5 is not a perfect square. To determine if a number is a perfect square, we need to find an integer whose square equals that number. For 5, we check:

• Calculating the square root of 5 gives approximately \( \sqrt{5} \approx 2.236 \).
• There is no integer \( n \) such that \( n^2 = 5 \).
• Therefore, 5 does not satisfy the definition of a perfect square.

Perfect squares are numbers like 1, 4, 9, 16, etc., where the square root is an integer. Since \( \sqrt{5} \) is not an integer, 5 is classified as a non-perfect square.

Rational numbers are those that can be expressed as a ratio of two integers, whereas irrational numbers cannot be expressed as such.

Key points distinguishing rational and irrational numbers:

• Rational numbers include integers and fractions where the denominator is not zero.
• Irrational numbers cannot be represented as fractions and have non-repeating, non-terminating decimal expansions.
• The square root of 5, \( \sqrt{5} \), is an example of an irrational number because it cannot be expressed as a simple fraction and its decimal representation continues indefinitely without repeating.

The square root of 5, denoted as \( \sqrt{5} \), is proven to be an irrational number through several mathematical arguments:

1. Direct Proof: Assume \( \sqrt{5} \) is rational, so \( \sqrt{5} = \frac{a}{b} \) where \( a \) and \( b \) are integers with no common factors. Squaring both sides gives \( 5 = \frac{a^2}{b^2} \), leading to \( 5b^2 = a^2 \). This implies \( a^2 \) is divisible by 5, thus \( a \) must also be divisible by 5 (since 5 is prime). Let \( a = 5k \), then \( 5b^2 = (5k)^2 = 25k^2 \), so \( b^2 = 5k^2 \) and hence \( b \) is also divisible by 5, contradicting our assumption that \( a \) and \( b \) have no common factors. Therefore, \( \sqrt{5} \) cannot be rational.
2. Contradiction to Integer Property: Another proof method involves considering \( \sqrt{5} \) as a root of the equation \( x^2 - 5 = 0 \). By the Rational Root Theorem, any rational root must be an integer divisor of the constant term (5) or its negative. Checking all possibilities (\(\pm 1, \pm 5\)), none satisfy \( x^2 - 5 = 0 \), confirming \( \sqrt{5} \) is irrational.
3. Continued Fraction: The continued fraction representation of \( \sqrt{5} \) reveals a non-repeating pattern, further supporting its irrationality. The continued fraction for \( \sqrt{5} \) is \( [2; 4, 4, 4, \ldots] \), showing it does not terminate or repeat.

Calculating \( \sqrt{5} \) involves several methods, each suited to different contexts and levels of precision:

1. Using a Calculator: The simplest method is using a scientific or graphing calculator, where you can directly compute \( \sqrt{5} \) to several decimal places.
2. Using a Computer: Computers can calculate \( \sqrt{5} \) with high precision using software libraries or built-in functions, providing accurate results for various applications.
3. Manual Calculation: For educational purposes, \( \sqrt{5} \) can be approximated manually using iterative methods such as the Babylonian method, starting with an initial guess and refining the approximation through successive iterations.

The square root of 5, denoted as √5, is an irrational number, meaning it cannot be expressed exactly as a fraction of two integers. However, it can be approximated or simplified in various forms:

1. Decimal Approximation: √5 ≈ 2.236067977...
2. Radical Form: √5 is typically left in its radical form unless required otherwise.
3. Continued Fraction: √5 can be represented as [2; 4, 4, 4, ...] in its continued fraction form.
4. Approximate Fractions: Although not exact, √5 can be expressed as close fractions such as 9/4 or 7/3.

Approximating the square root of 5, denoted as √5, involves expressing it as a fraction or a decimal to various degrees of accuracy:

1. Decimal Approximation: √5 ≈ 2.236067977...
2. Simple Fractions: While √5 is irrational, approximate fractions like 9/4 or 7/3 are close but not exact representations.
3. Continued Fraction: The continued fraction for √5 is [2; 4, 4, 4, ...], revealing its non-repeating nature.
4. Approximations in Geometry: In geometric applications, √5 often appears in dimensions where precise measurements are required.

The square root of 5, √5, has significant implications in geometry, particularly in the context of lengths and areas:

• Length: In a geometric context, √5 represents the length of the diagonal of a square with sides of length 1 unit.
• Area: It is also related to the area of rectangles or other shapes where √5 appears as a side length.
• Geometric Constructions: √5 is fundamental in geometric constructions involving right triangles and pentagons, reflecting its importance in geometric proofs and constructions.

The square root of 5, √5, plays a crucial role in various geometric applications:

• Diagonal Length: √5 represents the length of the diagonal of a square whose sides are of length 1 unit.
• Pythagorean Theorem: It appears in Pythagorean triples involving sides of right triangles, such as (2, 1, √5).
• Geometric Constructions: √5 is used in constructing regular pentagons and in certain trigonometric calculations.
• Area Calculations: It is involved in calculating the area of shapes where it serves as a side length, such as rectangles and non-square polygons.

In conclusion, the square root of 5, √5, is firmly established as an irrational number due to its non-repeating and non-terminating decimal expansion. Despite its irrationality, √5 holds significant mathematical and geometric importance:

1. It is crucial in geometric calculations involving right triangles, rectangles, and pentagons.
2. √5 appears in various mathematical proofs and constructions, showcasing its fundamental role in mathematical theory.
3. Its approximations and fractions provide practical utility in contexts where precise measurements are required.

Overall, understanding √5 contributes to a deeper appreciation of irrational numbers and their applications across different fields of mathematics and geometry.