Topic y square root of x: The equation y = √x is fundamental in mathematics, describing the relationship between two variables in a unique way. This article delves into the intricacies of the square root function, exploring its definition, properties, applications, and significance in various fields. Discover how understanding y = √x can enhance your mathematical knowledge and problem-solving skills.
Table of Content
- Understanding the Equation \(y = \sqrt{x}\)
- Introduction to the Square Root Function
- Mathematical Definition of y = √x
- Domain and Range of the Square Root Function
- Properties of y = √x
- Graphical Representation of y = √x
- Examples and Calculation Methods
- Real-world Applications of the Square Root Function
- Common Problems and Solutions Involving y = √x
- Advanced Topics Related to the Square Root Function
- Frequently Asked Questions About y = √x
- Conclusion and Summary
- YOUTUBE: Video hướng dẫn đồ thị hàm số y = √x một cách nhanh chóng và dễ hiểu, phù hợp cho người học toán.
Understanding the Equation \(y = \sqrt{x}\)
The equation \(y = \sqrt{x}\) is a fundamental mathematical function that describes a relationship between two variables, \(x\) and \(y\). It is widely used in various fields, including physics, engineering, and economics. This function is known as the square root function, and it is one of the simplest non-linear functions.
Definition
The square root of \(x\) is a number \(y\) such that when \(y\) is squared, the result is \(x\). Mathematically, this is represented as:
\[
y = \sqrt{x} \quad \text{where} \quad y^2 = x
\]
Properties
- Domain: The domain of the function \(y = \sqrt{x}\) is \(x \geq 0\). This is because the square root of a negative number is not defined in the set of real numbers.
- Range: The range of the function is \(y \geq 0\). Since the square root function produces non-negative outputs for non-negative inputs, \(y\) will always be zero or positive.
- Monotonicity: The function \(y = \sqrt{x}\) is monotonically increasing. This means that as \(x\) increases, \(y\) also increases.
- Continuity: The function is continuous for all \(x \geq 0\). There are no breaks, jumps, or holes in the graph of the function.
Graph of \(y = \sqrt{x}\)
The graph of the function \(y = \sqrt{x}\) is a curve that starts at the origin (0,0) and rises slowly to the right. Here is a table of values for some selected points:
| \(x\) | \(y = \sqrt{x}\) |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
Applications
- Physics: The square root function is used in physics to describe various phenomena, such as the relationship between the speed of a wave and its wavelength.
- Engineering: Engineers use the square root function in the analysis of signals and systems, especially in the context of power and energy calculations.
- Economics: In economics, the square root function can model diminishing returns and other economic behaviors.
Example Problems
- Find the value of \(y\) when \(x = 25\).
Solution: \[
y = \sqrt{25} = 5
\] - Determine \(x\) if \(y = 7\).
Solution: \[
y = \sqrt{x} \implies 7 = \sqrt{x} \implies x = 49
\]
The square root function is a versatile and essential tool in both theoretical and applied mathematics. Understanding its properties and applications can greatly enhance one's mathematical proficiency and problem-solving abilities.

READ MORE:
Introduction to the Square Root Function
The square root function, denoted as \(y = \sqrt{x}\), is a fundamental concept in mathematics. It describes the relationship where \(y\) is the positive number that, when squared, equals \(x\). This function is essential in various fields, including algebra, geometry, and calculus.
The square root function has several key properties and characteristics:
- Domain: The domain of \(y = \sqrt{x}\) includes all non-negative real numbers (\(x \geq 0\)). Negative numbers are excluded because the square root of a negative number is not a real number.
- Range: The range consists of all non-negative real numbers (\(y \geq 0\)). Since the square root function yields positive results for positive inputs, \(y\) will always be zero or greater.
- Monotonicity: The function is monotonically increasing, meaning as \(x\) increases, \(y\) also increases. This property ensures that the function does not decrease at any point.
- Continuity: The square root function is continuous for all \(x \geq 0\), with no breaks, jumps, or discontinuities in its graph.
Understanding the graph of \(y = \sqrt{x}\) is also crucial. The graph is a curve that starts at the origin (0,0) and rises steadily to the right. It is a common representation in mathematics and appears frequently in various applications.
Here is a table of values illustrating the relationship between \(x\) and \(y\):
| \(x\) | \(y = \sqrt{x}\) |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
The square root function is not only a theoretical concept but also has practical applications. It is used in solving quadratic equations, analyzing geometric shapes, and modeling real-world phenomena. Mastery of \(y = \sqrt{x}\) is essential for students and professionals in mathematics, science, and engineering.
Mathematical Definition of y = √x
The equation \(y = \sqrt{x}\) defines a mathematical relationship where \(y\) is the square root of \(x\). This means that \(y\) is a number which, when multiplied by itself, equals \(x\). Mathematically, this can be expressed as:
\[
y = \sqrt{x} \quad \text{where} \quad y^2 = x
\]
To understand this definition more clearly, consider the following properties and steps:
- Non-negative Input: For \(y = \sqrt{x}\) to hold true, \(x\) must be a non-negative number (\(x \geq 0\)). This is because the square root of a negative number is not defined within the set of real numbers.
- Output: The value of \(y\) will always be non-negative (\(y \geq 0\)), as the square root function returns the principal (non-negative) root.
Let's break down the computation of \(y = \sqrt{x}\) with a few examples:
| \(x\) | \(y = \sqrt{x}\) | Verification (\(y^2\)) |
|---|---|---|
| 0 | 0 | 0^2 = 0 |
| 1 | 1 | 1^2 = 1 |
| 4 | 2 | 2^2 = 4 |
| 9 | 3 | 3^2 = 9 |
| 16 | 4 | 4^2 = 16 |
| 25 | 5 | 5^2 = 25 |
In each case, the value of \(y\) is determined such that when squared, it equals the corresponding value of \(x\). This fundamental property is what defines the square root function.
The square root function is also intimately connected with the concept of exponents. Specifically, the square root of \(x\) can be represented as an exponent:
\[
\sqrt{x} = x^{\frac{1}{2}}
\]
This notation is particularly useful in advanced mathematics, allowing for easier manipulation of equations involving roots and powers.
Understanding the mathematical definition of \(y = \sqrt{x}\) is crucial for solving various types of equations and for analyzing functions in calculus and other branches of mathematics. Mastery of this concept provides a solid foundation for further study and application in numerous mathematical contexts.
Domain and Range of the Square Root Function
The domain and range of the square root function \(y = \sqrt{x}\) are fundamental concepts in understanding its behavior and applications. Let's explore these aspects in detail.
Domain of \(y = \sqrt{x}\)
The domain of a function is the set of all possible input values (x-values) that the function can accept. For the square root function \(y = \sqrt{x}\), the domain is restricted to non-negative real numbers. This is because the square root of a negative number is not defined within the set of real numbers. Mathematically, the domain is expressed as:
\[
\text{Domain} = \{x \in \mathbb{R} \mid x \geq 0\}
\]
In other words, \(x\) can take any value greater than or equal to zero. Here are a few examples:
- If \(x = 0\), then \(y = \sqrt{0} = 0\).
- If \(x = 4\), then \(y = \sqrt{4} = 2\).
- If \(x = 9\), then \(y = \sqrt{9} = 3\).
Range of \(y = \sqrt{x}\)
The range of a function is the set of all possible output values (y-values) that the function can produce. For the square root function \(y = \sqrt{x}\), the range is also restricted to non-negative real numbers. Since the square root function yields the principal (non-negative) root, \(y\) will always be zero or positive. Mathematically, the range is expressed as:
\[
\text{Range} = \{y \in \mathbb{R} \mid y \geq 0\}
\]
In other words, \(y\) can take any value greater than or equal to zero. Here are a few examples:
- If \(x = 0\), then \(y = 0\).
- If \(x = 1\), then \(y = 1\).
- If \(x = 16\), then \(y = 4\).
Graphical Representation
The domain and range of \(y = \sqrt{x}\) can be visualized through its graph. The graph of the square root function is a curve that starts at the origin (0,0) and extends infinitely to the right, rising slowly as \(x\) increases. The function is defined only for \(x \geq 0\) and \(y \geq 0\), creating a clear boundary for its domain and range.
Here is a table summarizing the domain and range for selected values:
| \(x\) | \(y = \sqrt{x}\) | Domain | Range |
|---|---|---|---|
| 0 | 0 | \(x \geq 0\) | \(y \geq 0\) |
| 1 | 1 | \(x \geq 0\) | \(y \geq 0\) |
| 4 | 2 | \(x \geq 0\) | \(y \geq 0\) |
| 9 | 3 | \(x \geq 0\) | \(y \geq 0\) |
| 16 | 4 | \(x \geq 0\) | \(y \geq 0\) |
Understanding the domain and range of the square root function \(y = \sqrt{x}\) is essential for solving equations and analyzing functions in various branches of mathematics. It ensures clarity in defining the input and output values and helps in the accurate interpretation of mathematical problems.
Properties of y = √x
The function \(y = \sqrt{x}\) has several important properties that define its behavior and applications. Understanding these properties is crucial for effectively using the square root function in mathematical problems. Below are the key properties of \(y = \sqrt{x}\):
1. Domain and Range
- Domain: The function is defined for all non-negative real numbers, \(x \geq 0\).
- Range: The output of the function is also non-negative, \(y \geq 0\).
2. Continuity
The square root function is continuous for all \(x \geq 0\). This means there are no breaks, jumps, or holes in the graph of the function. The function smoothly transitions from one point to another without any interruptions.
3. Monotonicity
The function \(y = \sqrt{x}\) is monotonically increasing. This means that as the value of \(x\) increases, the value of \(y\) also increases. There are no intervals where the function decreases.
4. Derivative
The derivative of \(y = \sqrt{x}\) can be calculated to understand the rate of change of the function. Using basic calculus, the derivative is found as follows:
\[
\frac{d}{dx}(\sqrt{x}) = \frac{1}{2\sqrt{x}}
\]
This indicates that the rate of change decreases as \(x\) increases. The derivative is undefined at \(x = 0\), highlighting a critical point of the function.
5. Integral
The integral of \(y = \sqrt{x}\) represents the area under the curve of the function. It can be computed as follows:
\[
\int \sqrt{x} \, dx = \frac{2}{3} x^{3/2} + C
\]
where \(C\) is the constant of integration.
6. Graphical Representation
The graph of \(y = \sqrt{x}\) is a curve that starts at the origin (0,0) and extends infinitely to the right, rising gradually. It is always located in the first quadrant of the Cartesian plane due to its non-negative domain and range.
7. Symmetry
The function \(y = \sqrt{x}\) does not exhibit symmetry about the y-axis or origin. It is solely defined in the first quadrant, making it an example of an asymmetric function.
8. Behavior at Endpoints
As \(x\) approaches 0, \(y\) approaches 0. Conversely, as \(x\) approaches infinity, \(y\) also approaches infinity, but at a decreasing rate due to the nature of the square root function.
Understanding these properties helps in analyzing and applying the square root function \(y = \sqrt{x}\) in various mathematical contexts, ensuring accurate problem-solving and deeper insights into its behavior.
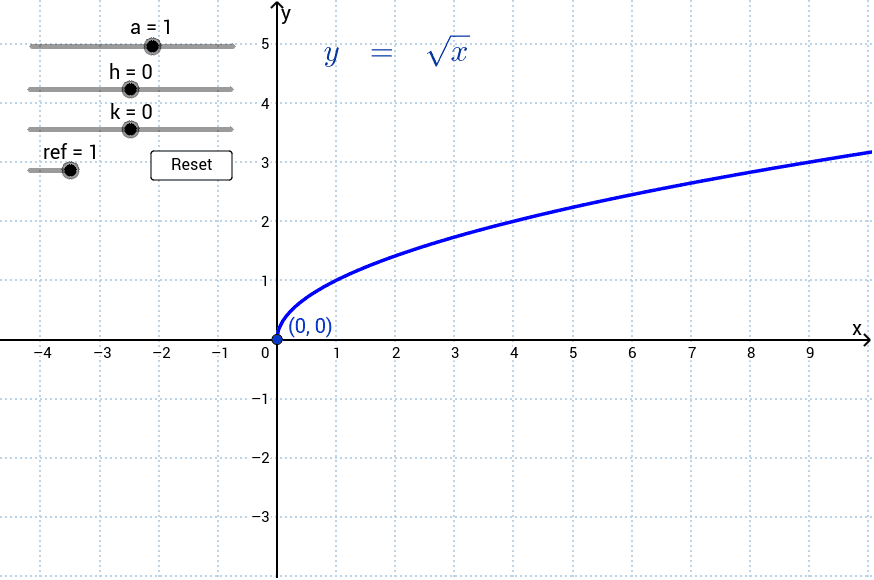
Graphical Representation of y = √x
The graph of the function \(y = \sqrt{x}\) provides a visual representation of the relationship between \(x\) and \(y\). Understanding the graphical features of this function helps in analyzing its behavior and properties.
1. Basic Shape and Plotting
The graph of \(y = \sqrt{x}\) is a curve that starts at the origin (0,0) and extends infinitely to the right. It is always located in the first quadrant of the Cartesian plane because both \(x\) and \(y\) are non-negative. The general shape is a gently increasing curve that flattens out as \(x\) increases.
Here is a step-by-step guide to plotting the graph:
- Start at the origin (0,0).
- Choose a few values for \(x\), such as 1, 4, 9, 16, and 25.
- Calculate the corresponding \(y\) values using \(y = \sqrt{x}\), which gives 1, 2, 3, 4, and 5, respectively.
- Plot these points on the Cartesian plane.
- Draw a smooth curve passing through the plotted points.
2. Key Points and Intervals
To better understand the graph, consider these key points:
- (0, 0): The graph starts at the origin, indicating that the square root of 0 is 0.
- (1, 1): At \(x = 1\), \(y = 1\) because the square root of 1 is 1.
- (4, 2): At \(x = 4\), \(y = 2\) because the square root of 4 is 2.
- (9, 3): At \(x = 9\), \(y = 3\) because the square root of 9 is 3.
- (16, 4): At \(x = 16\), \(y = 4\) because the square root of 16 is 4.
3. Slope and Rate of Change
The slope of the graph \(y = \sqrt{x}\) decreases as \(x\) increases. This means that the rate of change of \(y\) with respect to \(x\) slows down as \(x\) gets larger. Mathematically, the slope at any point is given by the derivative:
\[
\frac{d}{dx}(\sqrt{x}) = \frac{1}{2\sqrt{x}}
\]
This derivative shows that the slope is positive but decreases as \(x\) increases, leading to the characteristic flattening of the curve.
4. Asymptotic Behavior
As \(x\) approaches infinity, \(y = \sqrt{x}\) also approaches infinity, but at a decreasing rate. There are no horizontal or vertical asymptotes, but the graph continually rises without bound.
5. Symmetry
The function \(y = \sqrt{x}\) is not symmetric about the y-axis or the origin. It is defined only for non-negative \(x\) and \(y\) values, hence only occupying the first quadrant.
6. Graphing Example
Below is a table of selected points to help visualize the graph:
| \(x\) | \(y = \sqrt{x}\) |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
Understanding the graphical representation of \(y = \sqrt{x}\) helps in comprehending its properties and behavior, making it easier to apply in various mathematical contexts.
Examples and Calculation Methods
Understanding how to calculate the value of \(y = \sqrt{x}\) is essential for solving mathematical problems involving square roots. Below are detailed examples and methods for calculating the square root function.
Example Calculations
Let's start with some straightforward examples:
- Example 1: Calculate \(\sqrt{4}\).
- Since \(4 = 2 \times 2\), we have \(\sqrt{4} = 2\).
- Example 2: Calculate \(\sqrt{9}\).
- Since \(9 = 3 \times 3\), we have \(\sqrt{9} = 3\).
- Example 3: Calculate \(\sqrt{16}\).
- Since \(16 = 4 \times 4\), we have \(\sqrt{16} = 4\).
- Example 4: Calculate \(\sqrt{25}\).
- Since \(25 = 5 \times 5\), we have \(\sqrt{25} = 5\).
Calculation Methods
There are several methods to calculate the square root of a number, especially when the number is not a perfect square:
1. Prime Factorization
To find the square root using prime factorization, follow these steps:
- Factorize the number into its prime factors.
- Pair the prime factors.
- Take one number from each pair and multiply them.
Example: Calculate \(\sqrt{18}\).
- Prime factorization of 18: \(18 = 2 \times 3 \times 3\).
- Pair the factors: \(18 = 3 \times (3 \times 2)\).
- Take one number from each pair: \(\sqrt{18} = 3 \times \sqrt{2} \approx 4.24\).
2. Estimation Method
This method involves estimating the square root by finding two consecutive perfect squares between which the number lies:
- Identify the perfect squares closest to the given number.
- Estimate a value between these two squares.
- Refine the estimate by squaring it and comparing it to the original number.
Example: Estimate \(\sqrt{20}\).
- 20 lies between \(4^2 = 16\) and \(5^2 = 25\).
- Estimate closer to the lower bound: \(\sqrt{20} \approx 4.5\).
- Square the estimate: \(4.5^2 = 20.25\), which is close to 20.
- Refine the estimate: \(\sqrt{20} \approx 4.47\).
3. Long Division Method
This method is useful for more precise calculations:
- Group the digits of the number in pairs from right to left.
- Find the largest number whose square is less than or equal to the first pair or single digit.
- Subtract the square of this number from the first pair or single digit, bringing down the next pair of digits.
- Double the number obtained in step 2, and find a digit to append that forms a new divisor which, when multiplied by the appended digit, is less than or equal to the current dividend.
- Repeat the process for the remaining pairs of digits.
Example: Calculate \(\sqrt{529}\) using long division:
- Group digits: \(529\) becomes \(\overline{5}\overline{29}\).
- Find the largest number whose square is \(\leq 5\): \(2\) (since \(2^2 = 4\)).
- Subtract \(4\) from \(5\), bringing down \(29\): \(129\).
- Double \(2\) to get \(4\). Find the digit to append: \(7\) (since \(47 \times 7 = 329\)).
- Thus, \(\sqrt{529} = 23\).
4. Using a Calculator
For quick and accurate results, a calculator can be used to find the square root:
- Enter the number into the calculator.
- Press the square root (√) function.
- Read the result displayed on the screen.
Example: Calculate \(\sqrt{50}\) using a calculator:
- Enter \(50\) into the calculator.
- Press the √ button.
- The display shows \(\sqrt{50} \approx 7.07\).
By mastering these methods, one can efficiently calculate square roots for various numbers, facilitating problem-solving in mathematics.
Real-world Applications of the Square Root Function
The square root function \(y = \sqrt{x}\) has numerous applications across various fields. Its utility extends beyond pure mathematics to practical scenarios in science, engineering, finance, and more. Below, we explore several real-world applications of the square root function.
1. Physics and Engineering
In physics and engineering, the square root function is frequently used to describe relationships between physical quantities:
- Wave Mechanics: The square root function is used to determine wave speed. For instance, the speed of a wave on a string is given by \(v = \sqrt{\frac{T}{\mu}}\), where \(T\) is the tension in the string and \(\mu\) is the mass per unit length.
- Stress and Strain: In material science, the square root function helps calculate stress and strain relationships, especially when dealing with fracture mechanics.
- Electrical Circuits: The root mean square (RMS) value of alternating current (AC) is calculated using the square root function to determine the effective voltage or current.
2. Finance
In finance, the square root function is pivotal in various calculations involving risk and return:
- Standard Deviation: The square root is used to calculate the standard deviation of investment returns, a measure of risk or volatility.
- Compound Interest: The square root function helps in determining compound interest and in the calculation of annuities.
- Black-Scholes Model: In options pricing, the Black-Scholes model uses the square root in the formula to determine the option's price.
3. Medicine
Medical fields utilize the square root function in various diagnostic and analytical techniques:
- Body Surface Area (BSA): The square root function is used to estimate BSA using the formula \(BSA = \sqrt{\frac{height \times weight}{3600}}\), which is crucial for dosing medication.
- Pharmacokinetics: The square root function helps in modeling how drugs are absorbed, distributed, metabolized, and excreted in the body.
4. Architecture and Construction
In architecture and construction, the square root function aids in various calculations for design and safety:
- Load Distribution: The square root function helps in calculating the load distribution on different structures to ensure stability and safety.
- Diagonal Measurements: To find the diagonal length of square or rectangular structures, the square root function is used, given by \(d = \sqrt{l^2 + w^2}\), where \(l\) is the length and \(w\) is the width.
5. Computer Science
In computer science, the square root function is fundamental in algorithm design and analysis:
- Search Algorithms: Algorithms such as binary search use square roots to optimize the search process in large datasets.
- Graphics Rendering: The square root function is used in calculating distances and rendering graphics in two and three-dimensional space.
6. Environmental Science
Environmental science applies the square root function in modeling and analysis:
- Population Growth: Models that predict population growth and spread often use square roots to describe certain growth patterns.
- Pollution Dispersion: The square root function helps model the dispersion of pollutants in the air and water, assisting in environmental impact assessments.
Example Calculations
To illustrate these applications, let's look at specific examples:
- Wave Speed Calculation:
- Given: \(T = 100\) N (tension), \(\mu = 0.25 \, \text{kg/m}\).
- Calculate: \(v = \sqrt{\frac{T}{\mu}} = \sqrt{\frac{100}{0.25}} = \sqrt{400} = 20 \, \text{m/s}\).
- Standard Deviation:
- Given: Returns = [2%, 4%, 4%, 4%, 5%, 5%, 7%].
- Mean = 4.4286%, Variance = 2.1224.
- Calculate: \(\text{Standard Deviation} = \sqrt{2.1224} \approx 1.46\%.\)
These examples highlight the practical importance of the square root function in real-world scenarios, showcasing its versatility and essential role in various disciplines.
Common Problems and Solutions Involving y = √x
Understanding and solving equations involving the square root function y = √x can sometimes be challenging. Here are some common problems and solutions:
-
Problem 1: Solving √x = a
To solve this equation, square both sides to eliminate the square root:
\[ \sqrt{x} = a \implies x = a^2 \]
Example: Solve √x = 3.
Solution: \[ x = 3^2 = 9 \]
-
Problem 2: Solving equations with square roots on both sides
Example: Solve √x = √(2x - 3).
Solution:
- Square both sides: \[ x = 2x - 3 \]
- Isolate x: \[ x - 2x = -3 \implies -x = -3 \implies x = 3 \]
- Verify the solution: \[ \sqrt{3} = \sqrt{2(3) - 3} \implies \sqrt{3} = \sqrt{3} \]
-
Problem 3: Extraneous solutions
Sometimes squaring both sides introduces extraneous solutions. Always verify solutions in the original equation.
Example: Solve √(2x + 3) = x - 1.
Solution:
- Square both sides: \[ 2x + 3 = (x - 1)^2 \implies 2x + 3 = x^2 - 2x + 1 \]
- Rearrange to form a quadratic equation: \[ x^2 - 4x - 2 = 0 \]
- Solve the quadratic equation using the quadratic formula: \[ x = \frac{4 \pm \sqrt{16 + 8}}{2} \implies x = \frac{4 \pm \sqrt{24}}{2} \implies x = 2 \pm \sqrt{6} \]
- Verify solutions: Substitute back into the original equation to check.

Advanced Topics Related to the Square Root Function
The square root function, \(y = \sqrt{x}\), has several advanced topics that extend its basic understanding. These include its behavior under transformations, complex square roots, and applications in various mathematical fields.
1. Transformations of the Square Root Function
Transformations involve shifting, stretching, or compressing the graph of the square root function. The general form is \(y = a\sqrt{b(x - h)} + k\), where:
- a - Vertical stretch or compression factor
- b - Horizontal stretch or compression factor
- h - Horizontal shift
- k - Vertical shift
Example: \(y = 2\sqrt{3(x - 1)} + 5\) represents a vertical stretch by 2, a horizontal compression by \(\frac{1}{\sqrt{3}}\), a shift to the right by 1 unit, and an upward shift by 5 units.
2. Square Roots of Negative Numbers
In real numbers, the square root of a negative number is not defined. However, in complex numbers, it is represented using the imaginary unit \(i\), where \(i^2 = -1\). Thus, \(\sqrt{-x} = i\sqrt{x}\).
Example: \(\sqrt{-4} = 2i\).
3. Square Root Functions in Calculus
The square root function is differentiable and integrable. Its derivative and integral are:
- Derivative: \(\frac{d}{dx}\sqrt{x} = \frac{1}{2\sqrt{x}}\)
- Integral: \(\int \sqrt{x} \, dx = \frac{2}{3}x^{3/2} + C\)
These properties are essential for solving various problems in calculus.
4. Applications in Differential Equations
Square root functions appear in solutions to certain differential equations. For instance, solving the differential equation \(\frac{dy}{dx} = \frac{1}{2\sqrt{x}}\) involves integrating the right-hand side to find \(y\).
5. Square Roots in Geometry
In geometry, the distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) in a plane is given by the distance formula, which involves a square root:
\[ \text{Distance} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
6. Properties of Square Roots
- The product of square roots: \(\sqrt{a} \cdot \sqrt{b} = \sqrt{ab}\)
- The quotient of square roots: \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
- The square root of a square: \(\sqrt{x^2} = |x|\)
7. Complex Square Roots
The square root of a complex number \(z = a + bi\) is given by:
\[ \sqrt{z} = \sqrt{a + bi} = \sqrt{\frac{\sqrt{a^2 + b^2} + a}{2}} + i \cdot \text{sgn}(b) \sqrt{\frac{\sqrt{a^2 + b^2} - a}{2}} \]
This formula is useful in various fields of engineering and physics where complex numbers are prevalent.
8. Real-World Applications
Square roots are used in numerous real-world applications, including physics (e.g., calculating speeds and distances), engineering (e.g., analyzing stress and strain), and finance (e.g., computing volatility in stock prices).
These advanced topics highlight the versatility and importance of the square root function in mathematics and its applications across different domains.
Frequently Asked Questions About y = √x
Here are some common questions and answers related to the square root function y = √x:
1. What is the domain of y = √x?
The domain of the function y = √x is all non-negative real numbers, which can be written as:
\(\{x \in \mathbb{R} \mid x \geq 0\}\)
2. What is the range of y = √x?
The range of the function y = √x is also all non-negative real numbers, expressed as:
\(\{y \in \mathbb{R} \mid y \geq 0\}\)
3. How do you solve y = √x for x?
To solve for x, you can square both sides of the equation:
\(y = \sqrt{x}\)
Square both sides:
\(y^2 = x\)
4. Is y = √x an increasing or decreasing function?
The function y = √x is an increasing function. This means that as x increases, y also increases.
5. Can y = √x be graphed? If so, how?
Yes, y = √x can be graphed. The graph is a curve that starts at the origin (0, 0) and increases to the right. Here is a step-by-step method to plot it:
- Determine the domain: \(x \geq 0\)
- Choose a set of x-values within the domain (e.g., 0, 1, 4, 9)
- Calculate the corresponding y-values: \(y = \sqrt{0} = 0\), \(y = \sqrt{1} = 1\), \(y = \sqrt{4} = 2\), \(y = \sqrt{9} = 3\)
- Plot the points (0,0), (1,1), (4,2), (9,3) on the coordinate plane
- Draw a smooth curve through the points
The resulting graph is a parabola opening to the right.
6. What are some properties of the function y = √x?
- Domain: \(x \geq 0\)
- Range: \(y \geq 0\)
- Increasing: The function is monotonically increasing for all \(x \geq 0\)
- Continuity: The function is continuous for all \(x \geq 0\)
- Non-negative: Both x and y are always non-negative
7. How does y = √x compare to other functions?
The function y = √x grows slower than linear functions (e.g., y = x) and quadratic functions (e.g., y = x^2). This is because the square root increases less rapidly than these functions as x increases.
8. Can the function y = √x have any negative values?
No, the function y = √x cannot have negative values since the square root of a non-negative number is always non-negative.
9. What are some applications of the square root function?
The square root function appears in various real-world applications such as physics (calculating velocities), engineering (signal processing), and finance (calculating volatility).
10. What happens when x is a fraction in y = √x?
When x is a fraction, the function y = √x still applies. For example, if x = 1/4, then y = √(1/4) = 1/2.
These are some frequently asked questions about the square root function y = √x. Understanding these concepts can help in grasping the fundamentals and advanced topics related to this function.
Conclusion and Summary
The square root function, represented by \( y = \sqrt{x} \), plays a crucial role in various fields of mathematics and real-world applications. This function is defined for all non-negative real numbers, meaning its domain is \( [0, \infty) \), and it produces non-negative outputs, giving it a range of \( [0, \infty) \).
Graphically, the square root function is represented as half of a parabola lying on its side, starting from the origin (0,0) and extending infinitely to the right. This reflects its unique properties: it is always increasing, never decreasing, and is bounded below by 0 but unbounded above.
The function \( y = \sqrt{x} \) also exhibits important mathematical properties:
- Monotonicity: The function is monotonically increasing over its entire domain. This means that as the input value \( x \) increases, the output value \( y \) also increases.
- Convexity: The function is convex upwards, indicating that the line segment between any two points on the graph will lie above or on the graph itself.
Understanding the domain and range of the square root function is essential for correctly applying it in various mathematical problems and real-world scenarios. For example, in physics, the square root function is used to calculate distances and magnitudes, while in finance, it can model growth rates and risk assessments.
In summary, the square root function is a fundamental mathematical tool with straightforward yet powerful characteristics. Its domain and range, graphical representation, and properties like monotonicity and convexity make it indispensable for solving a wide range of mathematical problems and practical applications.
Video hướng dẫn đồ thị hàm số y = √x một cách nhanh chóng và dễ hiểu, phù hợp cho người học toán.
Đồ thị nhanh y = √x
READ MORE:
Video hướng dẫn cách đồ thị các hàm số căn bậc hai bằng cách sử dụng biến đổi và vẽ các điểm một cách chi tiết và dễ hiểu.
Đồ thị Hàm Số Căn Bậc Hai Sử Dụng Biến Đổi và Vẽ Điểm