Topic x square root: Discover the fascinating world of the square root function with our comprehensive guide. Whether you're a student, teacher, or math enthusiast, understanding the square root of x is essential for mastering mathematical concepts and applications. Join us as we explore definitions, properties, calculation methods, and real-world applications of this fundamental mathematical operation.
Table of Content
- Understanding the Square Root Function
- Introduction to Square Root
- Definition of Square Root
- Mathematical Representation
- Properties of Square Root Function
- Examples of Square Roots
- Graph of Square Root Function
- Methods to Calculate Square Roots
- Prime Factorization Method
- Estimation and Averaging Method
- Using Calculators for Square Roots
- Square Roots in Geometry
- Square Roots in Physics
- Square Roots in Engineering
- Historical Background of Square Roots
- Common Misconceptions about Square Roots
- Advanced Topics in Square Roots
- Complex Square Roots
- Square Roots of Negative Numbers
- YOUTUBE: Video giải thích tại sao x mũ 1/2 có nghĩa là căn bậc hai. Xem ngay để hiểu rõ hơn về khái niệm này.
Understanding the Square Root Function
The square root function is a fundamental concept in mathematics. It involves finding a number that, when multiplied by itself, equals the given number. Mathematically, the square root of \(x\) is denoted as \(\sqrt{x}\).
Definition
The square root of a number \(x\) is a value that, when multiplied by itself, gives \(x\). It is expressed as:
\[ \sqrt{x} = y \]
where \(y \times y = x\).
Properties of the Square Root Function
- Non-negative Numbers: The square root of a non-negative number is also non-negative.
- Zero: The square root of zero is zero. \(\sqrt{0} = 0\).
- Positive Numbers: For any positive number \(x\), \(\sqrt{x}\) is also positive.
- Squares: If \(x = y^2\), then \(\sqrt{x} = y\).
Examples
- The square root of 4 is 2 because \(2 \times 2 = 4\). \(\sqrt{4} = 2\).
- The square root of 9 is 3 because \(3 \times 3 = 9\). \(\sqrt{9} = 3\).
- The square root of 16 is 4 because \(4 \times 4 = 16\). \(\sqrt{16} = 4\).
Square Root Function Graph
The graph of the square root function \(y = \sqrt{x}\) is shown below:

The graph starts at the origin (0,0) and increases slowly, showing that as \(x\) increases, \(\sqrt{x}\) also increases.
Calculating Square Roots
Square roots can be calculated using various methods, including:
- Prime Factorization: Breaking down a number into its prime factors can help find its square root.
- Estimation and Averaging: Guessing a value and refining it through averaging.
- Using a Calculator: Most modern calculators have a square root function.
Applications of Square Roots
Square roots are used in various fields, such as:
- Geometry: Calculating the length of the sides of a right triangle using the Pythagorean theorem.
- Physics: Determining the standard deviation in statistics.
- Engineering: Solving quadratic equations.

READ MORE:
Introduction to Square Root
The square root is a fundamental concept in mathematics, representing a value that, when multiplied by itself, yields the original number. It is symbolized by the radical sign (√). The square root of a number x is written as √x, and it plays a critical role in various mathematical operations and real-world applications.
Understanding the square root involves several key aspects:
- Definition: The square root of x is a number y such that y2 = x. This can be expressed as:
\[ \sqrt{x} = y \]
- Non-negative Numbers: For any non-negative number x, the square root is also non-negative. For example:
- The square root of 9 is 3, because 32 = 9.
- The square root of 16 is 4, because 42 = 16.
- Zero: The square root of zero is zero:
\[ \sqrt{0} = 0 \]
- Positive and Negative Roots: Every positive number x has two square roots: √x and -√x. However, by convention, the symbol √x refers to the positive root.
The concept of square roots is not only theoretical but also practical. It is used in various fields such as geometry, where it helps in calculating the lengths of sides in right triangles using the Pythagorean theorem, and in statistics, where it is used to determine standard deviation.
Definition of Square Root
The square root of a number is a value that, when multiplied by itself, gives the original number. It is one of the most basic operations in mathematics, essential for understanding more complex concepts. The square root of a number \(x\) is denoted as \(\sqrt{x}\).
Mathematically, if \(y\) is the square root of \(x\), then:
\[ y = \sqrt{x} \]
This implies that:
\[ y^2 = x \]
For example:
- If \( x = 9 \), then \(\sqrt{9} = 3\), because \( 3^2 = 9 \).
- If \( x = 16 \), then \(\sqrt{16} = 4\), because \( 4^2 = 16 \).
Here are some important points to consider about square roots:
- Non-negative Results: The square root of a non-negative number is always non-negative. For instance, \(\sqrt{25} = 5\) and not \(-5\), although \((-5)^2 = 25\).
- Zero: The square root of zero is zero. \(\sqrt{0} = 0\).
- Imaginary Numbers: For negative numbers, the square root is not a real number but an imaginary number. For example, \(\sqrt{-1} = i\), where \(i\) is the imaginary unit.
Square roots can be represented in different ways:
- Radical Form: \(\sqrt{x}\) is the most common form.
- Exponent Form: \(x^{1/2}\) is another way to represent the square root of \(x\).
In summary, the square root function is a crucial mathematical operation with diverse applications across various fields, including geometry, physics, engineering, and statistics.
Mathematical Representation
The square root of a number is represented in various mathematical forms, providing a flexible approach to calculations and problem-solving. The most common representations include radical form and exponent form.
Radical Form
The radical form uses the radical symbol (√) to denote the square root. For any non-negative number \(x\), the square root is represented as:
\[ \sqrt{x} \]
For example:
- \(\sqrt{4} = 2\), because \(2 \times 2 = 4\).
- \(\sqrt{25} = 5\), because \(5 \times 5 = 25\).
Exponent Form
The exponent form expresses the square root using fractional exponents. For any non-negative number \(x\), the square root can be represented as:
\[ x^{1/2} \]
For example:
- \(4^{1/2} = 2\), because \(2^2 = 4\).
- \(25^{1/2} = 5\), because \(5^2 = 25\).
Properties of Square Roots
Square roots possess unique properties that are useful in various mathematical contexts:
- Product Property: The square root of a product is the product of the square roots:
\[ \sqrt{ab} = \sqrt{a} \times \sqrt{b} \]
For example, \(\sqrt{36} = \sqrt{4 \times 9} = \sqrt{4} \times \sqrt{9} = 2 \times 3 = 6\).
- Quotient Property: The square root of a quotient is the quotient of the square roots:
\[ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \]
For example, \(\sqrt{\frac{25}{4}} = \frac{\sqrt{25}}{\sqrt{4}} = \frac{5}{2} = 2.5\).
- Even Powers: The square root of \(x^2\) is the absolute value of \(x\):
\[ \sqrt{x^2} = |x| \]
For example, \(\sqrt{(-3)^2} = \sqrt{9} = 3\).
Graphical Representation
The graph of the square root function \(y = \sqrt{x}\) is a curve that starts at the origin (0,0) and increases gradually. It is defined only for non-negative values of \(x\), as square roots of negative numbers are not real:

In conclusion, understanding the mathematical representation of square roots is essential for grasping their applications and properties in various fields of mathematics and science.
Properties of Square Root Function
The square root function, denoted as \( \sqrt{x} \), exhibits several unique properties that are fundamental to its application in mathematics. Understanding these properties allows for effective utilization of the square root function in various mathematical contexts.
Non-Negativity
The square root of a non-negative number is always non-negative:
\[ \sqrt{x} \geq 0 \text{ for all } x \geq 0 \]
For example:
- \(\sqrt{25} = 5\), not \(-5\).
- \(\sqrt{0} = 0\).
Product Property
The square root of a product is equal to the product of the square roots of the individual factors:
\[ \sqrt{ab} = \sqrt{a} \cdot \sqrt{b} \]
For example:
- \(\sqrt{36} = \sqrt{4 \cdot 9} = \sqrt{4} \cdot \sqrt{9} = 2 \cdot 3 = 6\).
Quotient Property
The square root of a quotient is equal to the quotient of the square roots of the numerator and the denominator:
\[ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \]
For example:
- \(\sqrt{\frac{25}{4}} = \frac{\sqrt{25}}{\sqrt{4}} = \frac{5}{2} = 2.5\).
Power Property
The square root of a number raised to an even power returns the absolute value of the base:
\[ \sqrt{x^2} = |x| \]
For example:
- \(\sqrt{(-3)^2} = \sqrt{9} = 3\).
Additive Inverse Property
The square root of a sum is not generally equal to the sum of the square roots. However, for specific cases involving perfect squares, it simplifies calculations:
\[ \sqrt{a + b} \ne \sqrt{a} + \sqrt{b} \]
Graph of the Square Root Function
The graph of the square root function \(y = \sqrt{x}\) is a curve that starts at the origin (0,0) and increases gradually. It is defined only for non-negative values of \(x\), as square roots of negative numbers are not real:

Continuity and Differentiability
The square root function is continuous for all non-negative \(x\). It is differentiable for \(x > 0\), with the derivative given by:
\[ \frac{d}{dx} \sqrt{x} = \frac{1}{2\sqrt{x}} \]
In summary, the properties of the square root function are integral to its application across various mathematical and scientific fields, providing a basis for solving equations and understanding geometric relationships.

Examples of Square Roots
Understanding square roots is easier with practical examples. Here, we will explore various examples to illustrate how square roots are calculated and applied.
Simple Examples
- The square root of 4 is 2, because \(2 \times 2 = 4\).
\[ \sqrt{4} = 2 \]
- The square root of 9 is 3, because \(3 \times 3 = 9\).
\[ \sqrt{9} = 3 \]
- The square root of 16 is 4, because \(4 \times 4 = 16\).
\[ \sqrt{16} = 4 \]
Fractional Examples
Square roots can also be applied to fractions:
- The square root of \(\frac{1}{4}\) is \(\frac{1}{2}\), because \(\left(\frac{1}{2}\right)^2 = \frac{1}{4}\).
\[ \sqrt{\frac{1}{4}} = \frac{1}{2} \]
- The square root of \(\frac{9}{16}\) is \(\frac{3}{4}\), because \(\left(\frac{3}{4}\right)^2 = \frac{9}{16}\).
\[ \sqrt{\frac{9}{16}} = \frac{3}{4} \]
Decimal Examples
Square roots of decimal numbers work similarly:
- The square root of 0.25 is 0.5, because \(0.5 \times 0.5 = 0.25\).
\[ \sqrt{0.25} = 0.5 \]
- The square root of 2.25 is 1.5, because \(1.5 \times 1.5 = 2.25\).
\[ \sqrt{2.25} = 1.5 \]
Examples with Large Numbers
Square roots are also applicable to larger numbers:
- The square root of 144 is 12, because \(12 \times 12 = 144\).
\[ \sqrt{144} = 12 \]
- The square root of 1024 is 32, because \(32 \times 32 = 1024\).
\[ \sqrt{1024} = 32 \]
Imaginary Numbers
When dealing with negative numbers, square roots involve imaginary numbers:
- The square root of -1 is \(i\), the imaginary unit.
\[ \sqrt{-1} = i \]
- The square root of -9 is 3i, because \(3i \times 3i = -9\).
\[ \sqrt{-9} = 3i \]
These examples highlight the versatility of square roots in various mathematical contexts, from simple integers and fractions to decimals and imaginary numbers.
Graph of Square Root Function
The graph of the square root function, \( y = \sqrt{x} \), is an important tool for visualizing how the function behaves. This function only takes non-negative values of \( x \) because the square root of a negative number is not a real number.
Plotting the Graph
To plot the graph of \( y = \sqrt{x} \), we follow these steps:
- Select a range of non-negative \( x \) values.
- Calculate the corresponding \( y \) values using the function \( y = \sqrt{x} \).
- Plot the points \((x, y)\) on a coordinate plane.
- Connect the points to form a smooth curve.
Key Points
Here are some key points to plot on the graph:
| x | y |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
Graph Characteristics
The graph of \( y = \sqrt{x} \) has the following characteristics:
- Domain: The function is defined for all \( x \geq 0 \).
- Range: The function outputs all \( y \geq 0 \).
- Shape: The graph starts at the origin (0,0) and increases gradually, forming a curve that gets less steep as \( x \) increases.
- Intercept: The graph intersects the origin, meaning the square root of 0 is 0.
- Monotonicity: The function is increasing, meaning as \( x \) increases, \( y \) also increases.
Graph Illustration
The following image illustrates the graph of \( y = \sqrt{x} \):

In summary, the graph of the square root function provides a clear visual representation of how the function behaves, showing the relationship between \( x \) and \( y \) in a smooth, continuous curve.
Methods to Calculate Square Roots
Calculating square roots can be done using various methods, each suitable for different situations. Below are some of the most common methods, explained step-by-step.
1. Prime Factorization
Prime factorization is a straightforward method for perfect squares:
- Factor the number into its prime factors.
- Pair the prime factors.
- Take one number from each pair and multiply them.
Example:
- Calculate \(\sqrt{36}\).
- Prime factorization of 36: \(36 = 2 \times 2 \times 3 \times 3\).
- Pairs: \((2, 2)\) and \((3, 3)\).
- Multiply one number from each pair: \(2 \times 3 = 6\).
\[ \sqrt{36} = 6 \]
2. Long Division Method
The long division method is useful for both perfect and non-perfect squares:
- Group the digits of the number in pairs, starting from the decimal point.
- Find the largest number whose square is less than or equal to the first pair or single digit. This is the first digit of the square root.
- Subtract the square of this number from the first pair and bring down the next pair of digits.
- Double the current quotient and find a new digit to append to it, which when multiplied by the new digit, gives a product less than or equal to the current dividend.
- Repeat the process until all pairs have been used.
Example:
- Calculate \(\sqrt{529}\):
- Group digits: 5 | 29.
- Find the largest number whose square is ≤ 5: 2 (since \(2^2 = 4\)).
- Subtract and bring down the next pair: \(5 - 4 = 1\), bring down 29 to get 129.
- Double 2 to get 4. Find the digit \(x\) such that \(4x \times x \leq 129\): \(43 \times 3 = 129\).
- The quotient is 23. Hence, \(\sqrt{529} = 23\).
\[ \sqrt{529} = 23 \]
3. Newton's Method (Heron's Method)
Newton's method is an iterative numerical technique suitable for approximating square roots:
- Choose an initial guess \(x_0\) (the closer to the actual square root, the better).
- Apply the iteration formula:
\[ x_{n+1} = \frac{1}{2} \left( x_n + \frac{S}{x_n} \right) \]
- Repeat until the difference between \(x_{n+1}\) and \(x_n\) is within the desired accuracy.
Example:
- Calculate \(\sqrt{10}\):
- Initial guess \(x_0 = 3\).
- First iteration:
\[ x_1 = \frac{1}{2} \left( 3 + \frac{10}{3} \right) = \frac{1}{2} \left( 3 + 3.33 \right) = 3.1667 \]
- Second iteration:
\[ x_2 = \frac{1}{2} \left( 3.1667 + \frac{10}{3.1667} \right) = 3.1623 \]
- Continue iterations until the desired accuracy is achieved.
Approximated value: \(\sqrt{10} \approx 3.1623\).
4. Using a Calculator
Most scientific calculators have a square root function (usually denoted as \(\sqrt{}\) or \(x^{1/2}\)):
- Enter the number for which you need the square root.
- Press the square root button.
Example:
- Calculate \(\sqrt{50}\) using a calculator. The display shows approximately 7.071.
These methods provide various ways to calculate square roots, from simple manual techniques to more advanced numerical methods, catering to different needs and levels of precision.
Prime Factorization Method
The prime factorization method is a systematic approach used to find the square root of a number without using a calculator. This method involves the following steps:
- Factorization: Begin by determining the prime factors of the given number.
- Pairing: Pair up the factors in twos, starting from the smallest, until all factors are paired.
- Product: Multiply each pair of factors.
- Result: The product obtained from step 3 is the square root of the original number.
Let's illustrate this with an example:
| Example: Find the square root of 144 using prime factorization method. |
| Step 1: Factorize 144: 144 = 24 * 32. |
| Step 2: Pair the factors: (2 * 2) * (3 * 3). |
| Step 3: Multiply the pairs: (2 * 2) * (3 * 3) = 4 * 9 = 36. |
| Step 4: Result: √144 = 6. |
This method is particularly useful in scenarios where precise calculation is needed and can be applied to both perfect squares and non-perfect squares.
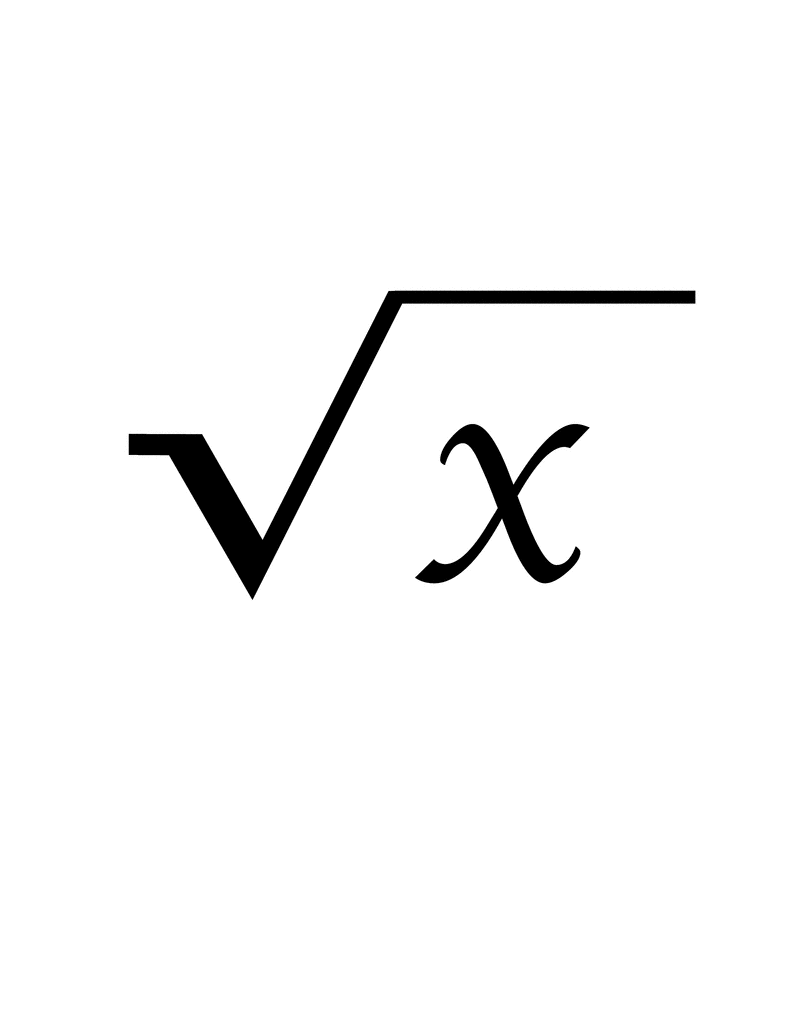
Estimation and Averaging Method
The estimation and averaging method is a practical approach to approximate the square root of a number without complex calculations. Here's how you can use this method:
- Estimate: Begin by making a reasonable estimate of the square root based on your knowledge of perfect squares close to the given number.
- Divide and Average: Divide the original number by your estimated square root. Average this result with your estimate to refine the approximation.
- Repeat: Repeat step 2 until your estimate stabilizes to a satisfactory degree of accuracy.
Let's illustrate this with an example:
| Example: Find an approximate value of √37 using estimation and averaging method. |
| Step 1: Estimate: √37 is close to √36 = 6. |
| Step 2: Divide: 37 / 6 ≈ 6.1667. Average: (6 + 6.1667) / 2 ≈ 6.0833. |
| Step 3: Repeat averaging: (6.0833 + 37 / 6.0833) / 2 ≈ 6.0828. |
This method provides a quick way to get a close approximation of the square root and is useful when precise calculation is not necessary or when a rough estimate is sufficient.
Using Calculators for Square Roots
Calculators are powerful tools for computing square roots quickly and accurately. Here’s how you can use calculators to find square roots:
- Enter the Number: Input the number for which you want to find the square root using the designated keys or functions on the calculator.
- Press the Square Root Button: Most scientific or advanced calculators have a specific button (usually labeled √x or x0.5) for calculating square roots.
- Result Display: Once you press the square root button, the calculator will display the square root of the entered number.
Let's see an example of using a calculator:
| Example: Find √225 using a calculator. |
| Step 1: Enter 225 into the calculator. |
| Step 2: Press the square root button. |
| Step 3: Result: √225 = 15. |
Using calculators for square roots is straightforward and ensures accuracy in computations, especially for numbers with many digits or non-perfect squares.
Square Roots in Geometry
Square roots play an essential role in various geometric calculations and concepts. Here’s how they are applied in geometry:
- Pythagorean Theorem: In a right triangle, the length of the hypotenuse (c) can be found using the formula \( c = \sqrt{a^2 + b^2} \), where \( a \) and \( b \) are the lengths of the other two sides.
- Area Calculations: Square roots are used to calculate the side length of a square given its area, \( s = \sqrt{A} \), where \( A \) is the area.
- Distance between Points: The distance between two points in a Cartesian coordinate system is determined using the distance formula \( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \).
- Volume of Cubes and Cuboids: Square roots are involved in finding the edge length of a cube or cuboid given its volume.
- Circle Properties: The radius of a circle can be calculated using the square root of its area, \( r = \sqrt{A/\pi} \), where \( A \) is the area of the circle.
Understanding square roots in geometry enables accurate measurement, calculation of dimensions, and exploration of spatial relationships, contributing significantly to geometric problem-solving and design.
Square Roots in Physics
Square roots are fundamental in physics and are used in various calculations and formulas. Here are some key applications of square roots in physics:
- Kinematics: Square roots are used to find velocities and accelerations from equations involving squared terms, such as in equations of motion.
- Energy Calculations: In kinetic energy calculations, the square root of mass times squared velocity (\( \sqrt{mv^2} \)) helps determine the magnitude of kinetic energy.
- Wave Mechanics: In wave equations, square roots appear in determining wave amplitudes and wave velocities.
- Electricity and Magnetism: Square roots are involved in calculating electric field strengths, magnetic field strengths, and potentials using formulas derived from Coulomb's law and Maxwell's equations.
- Quantum Mechanics: Square roots play a role in the Schrödinger equation, where they are used to find probabilities of quantum states and the normalization of wave functions.
Understanding and applying square roots in physics allow for precise calculations and predictions in fields ranging from mechanics to electromagnetism and quantum theory, contributing to advances in technology and scientific understanding.

Square Roots in Engineering
Square roots are extensively utilized in engineering for a variety of calculations and applications. Here are some significant ways in which square roots are used in engineering:
- Structural Analysis: Engineers use square roots in calculations involving stress, strain, and material properties to ensure structural integrity.
- Signal Processing: Square roots are essential in signal processing algorithms for calculating root mean square (RMS) values and signal amplitude.
- Power Systems: Square roots are used in electrical engineering to calculate the magnitude of AC voltages and currents in power systems.
- Fluid Dynamics: Engineers apply square roots in fluid mechanics to calculate velocities, pressures, and flow rates in pipes and channels.
- Control Systems: Square roots are used in control engineering for determining the magnitudes of transfer functions and stability criteria.
- Material Science: In material science, square roots are used to calculate thermal conductivity, diffusion coefficients, and other material properties.
Mastering the application of square roots in engineering enhances precision in design, analysis, and optimization processes, contributing to the development of efficient and safe engineering solutions.
Historical Background of Square Roots
The concept of square roots has a rich historical background dating back to ancient civilizations. Here's a brief overview of the historical development:
- Ancient Mesopotamia: Babylonian mathematicians around 2000 BC utilized algorithms to approximate square roots, as evidenced by clay tablets.
- Ancient Egypt: Egyptian mathematicians, around 1650 BC, developed geometric methods for finding square roots, often using visual representations of squares and their areas.
- Ancient Greece: Greek mathematicians, including Pythagoras and Euclid, explored the properties of squares and square roots, laying the foundation for geometric proofs and theoretical understanding.
- Islamic Golden Age: Scholars like Al-Khwarizmi in the 9th century contributed significantly to algebraic methods for solving quadratic equations, which involve square roots.
- Renaissance and Enlightenment: European mathematicians during the Renaissance and Enlightenment periods further developed algebraic techniques for calculating square roots and expanding their applications.
- Modern Era: With the advent of calculators and computers, the computation of square roots became more accessible and precise, leading to widespread practical applications in science, engineering, and everyday life.
The historical evolution of square roots reflects humanity's ongoing quest for mathematical understanding and practical applications, shaping the development of mathematics and its applications in various fields.
Common Misconceptions about Square Roots
Despite their fundamental role in mathematics, square roots are sometimes misunderstood. Here are some common misconceptions:
- Square roots of negative numbers: It is often incorrectly believed that square roots of negative numbers are not real. In fact, they are real and are represented as complex numbers.
- Exactness in calculations: People may think that square roots always result in exact integers or fractions. In reality, square roots of most numbers are irrational and have infinite decimal expansions.
- Calculation difficulty: Many assume that calculating square roots without a calculator is exceedingly complex. While some methods can be intricate, various techniques simplify the process.
- Application limitations: Some believe that square roots are only applicable in theoretical mathematics. However, they are extensively used in practical fields like engineering, physics, and finance.
- Complexity in higher mathematics: There's a misconception that understanding square roots requires advanced mathematical knowledge. Basic concepts can be grasped with elementary education, while deeper understanding comes with further study.
Clarifying these misconceptions fosters a better understanding of square roots and their practical applications, enhancing mathematical literacy and problem-solving skills.
Advanced Topics in Square Roots
Advanced topics related to square roots delve into complex mathematical concepts and applications beyond basic calculations. Here are some key areas:
- Complex Square Roots: Square roots of negative numbers extend into the realm of complex numbers, crucial in fields like electrical engineering and quantum mechanics.
- Square Roots of Negative Numbers: Understanding how to handle square roots of negative numbers is essential in algebraic contexts and advanced mathematical modeling.
- Square Roots in Higher Mathematics: In abstract algebra and number theory, square roots are studied in the context of fields, rings, and other algebraic structures.
- Applications in Calculus: Square roots appear in calculus through the study of limits, derivatives, and integrals involving square root functions.
- Matrix Square Roots: In linear algebra, square roots of matrices are explored, playing a role in eigenvalue problems and matrix decomposition techniques.
- Computational Methods: Advanced numerical methods for computing square roots, such as iterative algorithms and convergence criteria, are developed for precision and efficiency.
Exploring these advanced topics deepens understanding of square roots across various disciplines, highlighting their theoretical foundations and practical applications in advanced mathematics and scientific research.

Complex Square Roots
Complex square roots involve finding the roots of a complex number. For any complex number \( z = a + bi \), the square roots can be determined using polar coordinates and Euler's formula.
To find the square roots of a complex number, follow these steps:
- Convert the complex number to polar form: \( z = r(\cos \theta + i \sin \theta) \) where \( r = \sqrt{a^2 + b^2} \) and \( \theta = \tan^{-1} \left( \frac{b}{a} \right) \).
- Use the polar form to find the square roots: \( \sqrt{z} = \sqrt{r} \left( \cos \frac{\theta}{2} + i \sin \frac{\theta}{2} \right) \) and \( \sqrt{z} = \sqrt{r} \left( \cos \left( \frac{\theta + 2\pi}{2} \right) + i \sin \left( \frac{\theta + 2\pi}{2} \right) \right) \).
For example, to find the square roots of \( i \):
- Express \( i \) in polar form: \( i = 1(\cos \frac{\pi}{2} + i \sin \frac{\pi}{2}) \).
- Find the square roots:
- \( \sqrt{i} = \sqrt{1} \left( \cos \frac{\pi/2}{2} + i \sin \frac{\pi/2}{2} \right) = \cos \frac{\pi}{4} + i \sin \frac{\pi}{4} = \frac{\sqrt{2}}{2} + i\frac{\sqrt{2}}{2} \).
- \( \sqrt{i} = \sqrt{1} \left( \cos \frac{\pi/2 + 2\pi}{2} + i \sin \frac{\pi/2 + 2\pi}{2} \right) = \cos \frac{5\pi}{4} + i \sin \frac{5\pi}{4} = -\frac{\sqrt{2}}{2} - i\frac{\sqrt{2}}{2} \).
These steps illustrate the process of finding the square roots of any complex number. The properties of complex roots follow the same principles as those of real roots but extend into the complex plane, providing a comprehensive understanding of their behavior and applications in various fields.
Square Roots of Negative Numbers
In mathematics, the square root of a negative number introduces the concept of imaginary numbers. Since the square of any real number is non-negative, we cannot find a real number that is the square root of a negative number. To address this, we use the imaginary unit \( i \), which is defined as \( i = \sqrt{-1} \).
The square root of a negative number can be expressed as a multiple of \( i \). For any positive real number \( p \), the square root of \( -p \) is given by:
\( \sqrt{-p} = i\sqrt{p} \)
Here are some steps and examples to illustrate this concept:
- Identify the positive counterpart of the negative number.
- Compute the square root of the positive number.
- Multiply the result by \( i \) to get the square root of the negative number.
For example:
- \( \sqrt{-4} = \sqrt{4} \cdot i = 2i \)
- \( \sqrt{-9} = \sqrt{9} \cdot i = 3i \)
Let's break down the process step by step:
- Consider the negative number \( -25 \).
- Identify its positive counterpart, which is \( 25 \).
- Compute the square root of \( 25 \), which is \( 5 \).
- Multiply the result by \( i \), giving \( \sqrt{-25} = 5i \).
When dealing with equations, the square root of a negative number leads to complex solutions. For instance, the equation \( x^2 = -16 \) has the solutions:
\( x = \pm 4i \)
These solutions are complex numbers, which consist of a real part and an imaginary part. The imaginary unit \( i \) helps us extend the real number system to include solutions to such equations.
Understanding the properties of imaginary numbers is essential in higher mathematics, physics, and engineering. They are used to solve equations that have no real solutions and are integral to complex number theory.
In summary, the square root of a negative number is an imaginary number and can be written as a product of the imaginary unit \( i \) and the square root of the corresponding positive number.
Video giải thích tại sao x mũ 1/2 có nghĩa là căn bậc hai. Xem ngay để hiểu rõ hơn về khái niệm này.
Tại sao "x mũ 1/2" có nghĩa là căn bậc hai?
READ MORE:
Video giải thích căn bậc hai của x-bình phương và tại sao 90% học sinh trả lời sai câu hỏi này. Khám phá ngay để không mắc lỗi phổ biến này.
Căn bậc hai của X-Bình phương: Một câu hỏi cơ bản được 90% học sinh trả lời sai