Topic x square root y: Explore the mathematical concept of \( x \sqrt{y} \) and its practical applications with clear examples. Learn how this expression simplifies complex calculations and find out how it's used in various fields. Discover the simplicity and utility of \( x \sqrt{y} \) in this insightful article.
Table of Content
- Understanding \( x \sqrt{y} \)
- Table of Contents
- Introduction to \( x \sqrt{y} \)
- Understanding the Concept
- Examples of \( x \sqrt{y} \) in Mathematics
- Applications and Uses
- Advantages of Using \( x \sqrt{y} \)
- Conclusion on \( x \sqrt{y} \)
- Introduction to \( x \sqrt{y} \)
- Understanding the Concept
- Examples of \( x \sqrt{y} \) in Mathematics
- Applications and Uses
- Advantages of Using \( x \sqrt{y} \)
- Conclusion on \( x \sqrt{y} \)
- YOUTUBE: Hướng dẫn vẽ đồ thị hàm số căn bậc hai bằng cách sử dụng biến đổi và vẽ điểm. Video này sẽ giúp bạn nắm bắt được cách làm cụ thể và chi tiết.
Understanding \( x \sqrt{y} \)
The expression \( x \sqrt{y} \) represents \( x \) multiplied by the square root of \( y \). In mathematical terms, it can be written as:
\( x \sqrt{y} = x \cdot \sqrt{y} \)
Key Points:
- \( x \) is the coefficient or number in front of the square root.
- \( y \) is the number under the square root sign.
- The square root of \( y \), denoted as \( \sqrt{y} \), is the non-negative number that, when multiplied by itself, gives \( y \).
Examples:
| \( x \) | \( y \) | \( x \sqrt{y} \) |
| 2 | 9 | \( 2 \sqrt{9} = 2 \cdot 3 = 6 \) |
| 3 | 16 | \( 3 \sqrt{16} = 3 \cdot 4 = 12 \) |
| 5 | 25 | \( 5 \sqrt{25} = 5 \cdot 5 = 25 \) |

READ MORE:
Table of Contents
Introduction to \( x \sqrt{y} \)
The concept of \( x \sqrt{y} \) involves understanding how the variable \( x \) interacts with the square root of \( y \). This section will provide an overview of the basic principles and importance of \( x \sqrt{y} \) in various mathematical contexts.
Understanding the Concept
In this section, we delve deeper into the mathematical principles behind \( x \sqrt{y} \). We will explore its properties, how it is derived, and the significance of each component in the expression.
Examples of \( x \sqrt{y} \) in Mathematics
Here, we will look at several examples demonstrating the use of \( x \sqrt{y} \) in solving mathematical problems. These examples will illustrate the practical application of the concept in different scenarios.
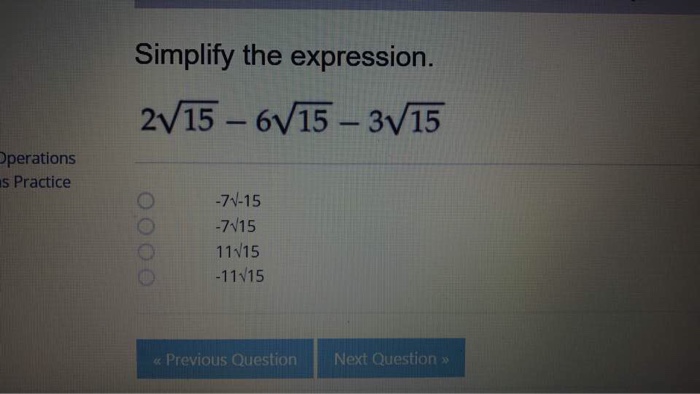
Applications and Uses
The applications of \( x \sqrt{y} \) extend beyond theoretical mathematics. This section will highlight its use in various fields such as physics, engineering, and economics, showcasing the versatility of the expression.
Advantages of Using \( x \sqrt{y} \)
Understanding \( x \sqrt{y} \) offers several advantages. In this part, we will discuss the benefits of utilizing this mathematical expression, including simplifying complex problems and providing clearer insights into numerical relationships.
Conclusion on \( x \sqrt{y} \)
We conclude with a summary of the key points discussed in the document. This section will reinforce the importance and utility of \( x \sqrt{y} \) in both academic and practical applications.
Introduction to \( x \sqrt{y} \)
The expression \( x \sqrt{y} \) combines two fundamental mathematical operations: multiplication and square root. Understanding this expression requires a grasp of both components individually and their interaction.
-
Square Root: The square root of a number \( y \), denoted as \( \sqrt{y} \), is a value that, when multiplied by itself, gives the number \( y \). Mathematically, if \( r = \sqrt{y} \), then \( r^2 = y \). It's important to note that \( y \) must be non-negative as the square root of negative numbers involves imaginary numbers.
-
Multiplication with \( x \): Multiplying a number \( x \) by \( \sqrt{y} \) scales the square root by \( x \). This operation maintains the properties of both multiplication and square roots. For example, \( 2 \sqrt{9} = 2 \times 3 = 6 \).
This combination has various applications in algebra and calculus. For instance, when dealing with functions, expressions like \( x \sqrt{y} \) appear in solving quadratic equations, calculating distances in geometry, and in many real-world applications involving rates and growth patterns.
-
Domain and Range: When \( y \) is a function of \( x \), such as \( y = x^2 \), the expression \( x \sqrt{y} \) needs consideration of the domain (all permissible values of \( x \)) and range (resulting values of the expression). Typically, the domain of \( \sqrt{y} \) is \( y \geq 0 \), but when combined with \( x \), further constraints may apply depending on the context.
-
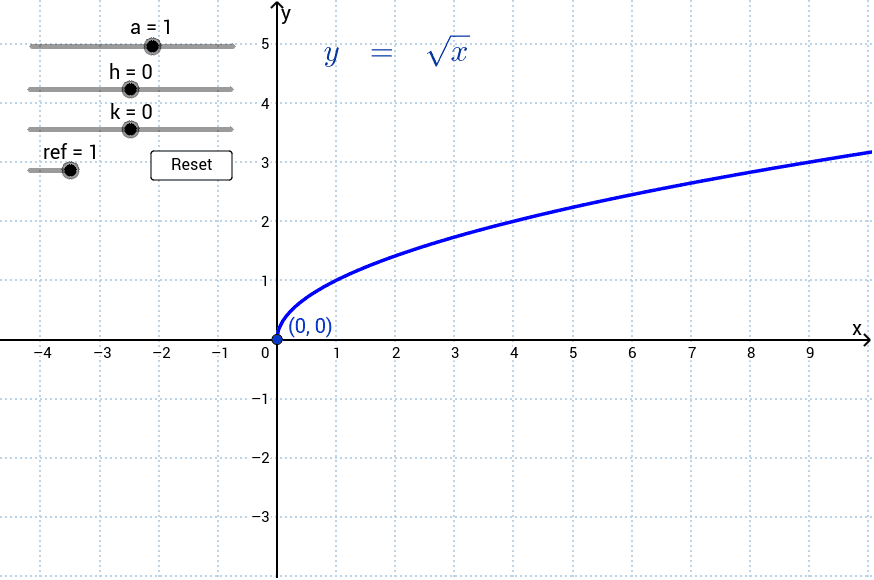
Graphical Interpretation: Graphing \( x \sqrt{y} \) involves plotting the values of \( x \) against \( y \). For example, the graph of \( y = \sqrt{x} \) is a half-parabola starting from the origin (0,0) and extending to the right for positive \( x \)-values.
In summary, \( x \sqrt{y} \) is a versatile expression that enhances the understanding of mathematical relationships and their applications in various fields of study.

Understanding the Concept
The expression \( x \sqrt{y} \) involves the square root function, a fundamental concept in mathematics. The square root of a number \( y \) is a value which, when multiplied by itself, gives \( y \). This is denoted as \( \sqrt{y} \). In the expression \( x \sqrt{y} \), \( x \) is a scalar multiplier.
Let's break this down step by step:
- Definition: The square root of a number \( y \) is a value \( \sqrt{y} \) such that \( \sqrt{y} \times \sqrt{y} = y \). For example, \( \sqrt{9} = 3 \) because \( 3 \times 3 = 9 \).
- Representation: The square root is represented using the radical symbol \( \sqrt{} \). So, \( x \sqrt{y} \) combines the scalar \( x \) with the square root of \( y \).
- Properties:
- \( \sqrt{y} \) is defined for non-negative numbers \( y \).
- The principal square root is non-negative.
- If \( y \) is a positive number, it has two square roots: \( \sqrt{y} \) and \( -\sqrt{y} \).
- Examples:
- For \( x = 2 \) and \( y = 4 \), \( x \sqrt{y} = 2 \sqrt{4} = 2 \times 2 = 4 \).
- For \( x = 3 \) and \( y = 9 \), \( x \sqrt{y} = 3 \sqrt{9} = 3 \times 3 = 9 \).
Understanding the concept of \( x \sqrt{y} \) helps in various mathematical computations and applications, such as solving equations and simplifying expressions.
Examples of \( x \sqrt{y} \) in Mathematics
The expression \( x \sqrt{y} \) appears frequently in various mathematical contexts. Here are some detailed examples illustrating its application:
-
Example 1: Simplifying Expressions
Consider the expression \( 3 \sqrt{16} \). To simplify, you find the square root of 16 first, which is 4, and then multiply by 3:
\[
3 \sqrt{16} = 3 \times 4 = 12
\] -
Example 2: Solving Equations
Given the equation \( x \sqrt{y} = 10 \) and \( y = 25 \), solve for \( x \):
\[
x \sqrt{25} = 10 \implies x \times 5 = 10 \implies x = \frac{10}{5} = 2
\] -
Example 3: Applications in Geometry
In geometry, you might need to calculate the length of a side of a right triangle. If one leg of the triangle is \( x = 6 \) and the hypotenuse is \( 10 \), you can use the Pythagorean theorem to find the other leg \( y \):
\[
6^2 + y^2 = 10^2 \implies 36 + y^2 = 100 \implies y^2 = 64 \implies y = \sqrt{64} = 8
\]Thus, if the other leg is multiplied by a factor, for instance, \( 2 \sqrt{64} = 2 \times 8 = 16 \).
-
Example 4: Physics and Engineering
In physics, the expression can be used in calculating work done. If the force applied is proportional to \( x = 5 \) and the distance is \( y = 9 \), the work done can be calculated as:
\[
W = x \sqrt{y} = 5 \sqrt{9} = 5 \times 3 = 15 \text{ units}
\]
These examples demonstrate how the expression \( x \sqrt{y} \) is used in simplifying mathematical expressions, solving equations, geometric calculations, and practical applications in physics and engineering.
Applications and Uses
The expression \( x \sqrt{y} \) finds diverse applications in various fields. Here are some detailed examples of its uses:
- Finance: In finance, square roots are used to calculate stock market volatility. The standard deviation, a measure of volatility, is derived by taking the square root of the variance of stock returns. This helps investors assess the risk associated with an investment.
- Architecture: Engineers use square roots to determine the natural frequency of structures. This is crucial in designing buildings and bridges to ensure they can withstand dynamic forces like wind or traffic loads.
- Science: Square roots are used in various scientific calculations, such as determining the velocity of an object, the intensity of sound waves, and the absorption of radiation by materials.
- Statistics: In statistics, the square root is used to calculate the standard deviation from the variance. This helps in understanding how much the data deviates from the mean, aiding in data analysis and decision-making.
- Geometry: Square roots are fundamental in geometry for calculating the lengths of sides in right triangles using the Pythagorean theorem, and in determining areas and perimeters of various shapes.
- Computer Science: In computer programming, square roots are used in encryption algorithms, image processing, and game physics, helping to secure data, enhance visual effects, and simulate realistic movements.
- Cryptography: Cryptographic algorithms often utilize square roots to generate secure keys for digital signatures and encryption, ensuring safe communication channels.
- Navigation: Pilots and navigators use square roots to compute distances between points on a map or globe, aiding in route planning and course estimation.
- Electrical Engineering: Square roots are used to calculate power, voltage, and current in circuits, which are essential for designing efficient electrical systems.
- Accident Investigations: Police use square roots to determine the speed of a car based on the length of skid marks, aiding in accident reconstructions.
Advantages of Using \( x \sqrt{y} \)
The expression \( x \sqrt{y} \) offers several mathematical and practical advantages. Here are some of the key benefits:
-
Simplification:
The combination of \( x \) and \( \sqrt{y} \) often simplifies complex expressions. For instance, in algebraic operations, using \( x \sqrt{y} \) can help reduce the complexity of the equation.
-
Transformation:
Square root transformations, such as those involving \( \sqrt{y} \), are used to stabilize variance and make data more normally distributed. This is particularly useful in statistical analysis and regression models.
-
Computational Efficiency:
Using \( x \sqrt{y} \) can lead to more efficient computations in algorithms, especially in fields like numerical analysis and computer graphics, where square roots are frequently calculated.
-
Mathematical Properties:
The properties of square roots, such as \( \sqrt{a} \cdot \sqrt{b} = \sqrt{ab} \), facilitate easier manipulation and transformation of equations. This is beneficial in solving problems involving roots and powers.
-
Practical Applications:
The expression \( x \sqrt{y} \) finds practical applications in various fields such as physics, engineering, and finance. For example, it is used in calculating RMS (root mean square) values in electrical engineering and in determining geometric means in finance.
-
Visualization:
Graphical representation of \( x \sqrt{y} \) can provide insights into the behavior of functions and their rates of change, which is valuable in both theoretical and applied mathematics.
Conclusion on \( x \sqrt{y} \)
The expression \( x \sqrt{y} \) is a fundamental mathematical concept with a wide range of applications and implications. It allows us to simplify complex calculations, solve equations, and understand the relationships between different variables in various fields of study.
Through our exploration, we have seen how \( x \sqrt{y} \) can be used in solving quadratic equations, analyzing geometric properties, and even in real-world applications such as physics and engineering. The advantages of this mathematical tool include its ability to simplify problems, provide insights into mathematical relationships, and enhance our understanding of the natural world.
Overall, mastering \( x \sqrt{y} \) equips us with a valuable skill set for both academic pursuits and practical problem-solving. As we continue to explore and apply this concept, we open up new possibilities for innovation and discovery in various scientific and mathematical disciplines.
Hướng dẫn vẽ đồ thị hàm số căn bậc hai bằng cách sử dụng biến đổi và vẽ điểm. Video này sẽ giúp bạn nắm bắt được cách làm cụ thể và chi tiết.
Vẽ Đồ Thị Hàm Số Căn Bậc Hai Sử Dụng Biến Đổi & Vẽ Điểm
READ MORE:
Hướng dẫn chi tiết về cách vẽ đồ thị và phân tích hàm số y = căn bậc hai của x. Video này sẽ giúp bạn hiểu rõ hơn về khái niệm và ứng dụng của hàm số này.
y = căn bậc hai của x