Topic square root of 5 simplified: Discover the intriguing world of square roots with our detailed guide on simplifying the square root of 5. Learn about its properties, calculation methods, and applications in mathematics. This article will help you understand the importance and the steps to simplify √5, providing clear explanations and practical examples for a better grasp of the concept.
Table of Content
- Simplifying the Square Root of 5
- Introduction to Square Roots
- Understanding the Square Root of 5
- Simplifying Square Roots
- Step-by-Step Guide to Simplify the Square Root of 5
- Properties of the Square Root of 5
- Decimal Approximation of the Square Root of 5
- Geometric Interpretation of the Square Root of 5
- Using Long Division Method to Calculate Square Roots
- Applications of the Square Root of 5 in Mathematics
- Common Questions and Answers about Square Roots
- Practice Problems and Solutions
- Additional Resources and Tools
- Conclusion
- YOUTUBE: Đơn giản hóa căn bậc hai | Toán học cùng Thầy J
Simplifying the Square Root of 5
The square root of 5, represented as \(\sqrt{5}\), is an irrational number, meaning it cannot be expressed as a simple fraction and has an infinite number of decimals.
Value of \(\sqrt{5}\)
The decimal approximation of \(\sqrt{5}\) to five decimal places is:
\(\sqrt{5} \approx 2.23607\)
Methods to Simplify Square Roots
Simplifying square roots involves breaking down the number inside the radical into its prime factors and then simplifying using the property of square roots:
\(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\)
Example Problems
- Simplify \(\sqrt{12}\):
- 12 can be factored into 4 and 3.
- \(\sqrt{12} = \sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3} = 2\sqrt{3}\)
- Simplify \(\sqrt{45}\):
- 45 can be factored into 9 and 5.
- \(\sqrt{45} = \sqrt{9 \times 5} = \sqrt{9} \times \sqrt{5} = 3\sqrt{5}\)
Properties of \(\sqrt{5}\)
\(\sqrt{5}\) is an irrational number because 5 is a prime number and cannot be expressed as a product of a perfect square and another number.
In exponent form, it is represented as \(5^{\frac{1}{2}}\).
Geometric Interpretation
Geometrically, \(\sqrt{5}\) can be visualized as the diagonal of a rectangle with side lengths 1 and 2, based on the Pythagorean theorem.
Calculating \(\sqrt{5}\) Using Long Division Method
- Make an initial estimate and set up the division.
- Divide and find the average repeatedly until the desired precision is achieved.
Applications
\(\sqrt{5}\) appears in various mathematical and geometric contexts, such as in solving quadratic equations and in trigonometry.
Common Questions
| Question | Answer |
| What is \(\sqrt{5}\) in simplest radical form? | \(\sqrt{5}\) cannot be simplified further as it is already in its simplest form. |
| Why is \(\sqrt{5}\) irrational? | Because 5 is a prime number and does not have a pair of factors that are perfect squares. |

READ MORE:
Introduction to Square Roots
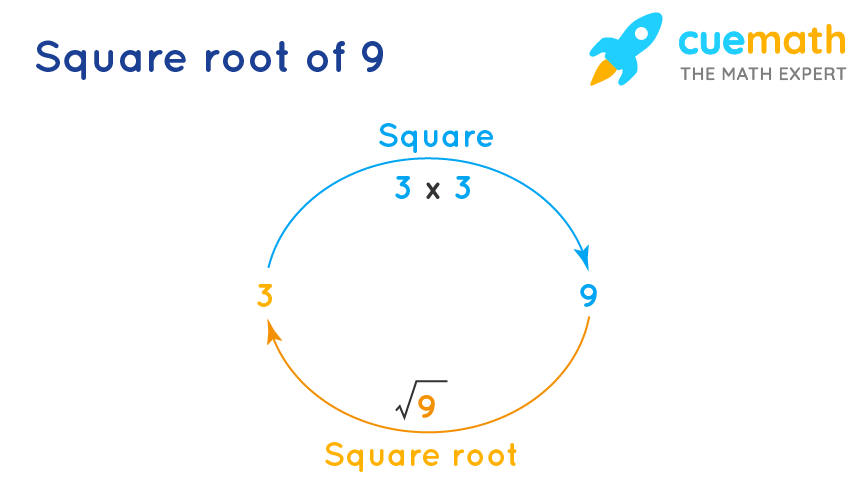
Square roots are fundamental mathematical operations that find the value which, when multiplied by itself, yields the original number. The square root of a number \( x \) is denoted as \( \sqrt{x} \). For instance, the square root of 9 is 3, because \( 3 \times 3 = 9 \). Square roots are essential in various fields of mathematics and science, providing solutions to quadratic equations and describing geometric properties.
There are several key properties of square roots:
- Non-Negativity: For any real number \( x \), \( \sqrt{x} \) is always non-negative.
- Product Property: The square root of a product is the product of the square roots: \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \).
- Quotient Property: The square root of a quotient is the quotient of the square roots: \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \), where \( b \neq 0 \).
- Irrational Numbers: Square roots of non-perfect squares are irrational numbers, meaning they cannot be expressed as simple fractions.
To simplify square roots, we often factor the number into its prime factors and pair them to move factors outside the radical. For example:
- \( \sqrt{12} = \sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3} = 2\sqrt{3} \)
- \( \sqrt{45} = \sqrt{9 \times 5} = \sqrt{9} \times \sqrt{5} = 3\sqrt{5} \)
The square root of 5 (\( \sqrt{5} \)) is an irrational number, approximately equal to 2.23607. It cannot be simplified further into a simpler radical form because 5 is a prime number and does not have any square factors other than 1.
Understanding and working with square roots is crucial for solving algebraic equations, analyzing geometric shapes, and performing various scientific calculations. This guide will provide you with the knowledge and tools to simplify and work with square roots effectively.
Understanding the Square Root of 5
The square root of 5, denoted as \( \sqrt{5} \), is a fascinating mathematical concept. As an irrational number, \( \sqrt{5} \) cannot be expressed as a simple fraction and has an infinite number of non-repeating decimals. It is approximately equal to 2.23607.
Let's explore the properties and calculation methods of \( \sqrt{5} \):
- Radical Form: The square root of 5 in its simplest radical form is \( \sqrt{5} \). Since 5 is a prime number, it does not have any square factors other than 1, making \( \sqrt{5} \) already simplified.
- Exponential Form: In exponential notation, \( \sqrt{5} \) is expressed as \( 5^{1/2} \) or \( 5^{0.5} \).
- Decimal Approximation: The decimal value of \( \sqrt{5} \) is approximately 2.23607. This value continues infinitely without repeating.
To understand the calculation of \( \sqrt{5} \), let's consider the long division method:
- Estimate a close value to the square root of 5, such as 2.2, because \( 2.2^2 = 4.84 \) and \( 2.3^2 = 5.29 \).
- Use the division method to refine this estimate:
- Set up 5 with a pair of zeros: 5.00.
- Determine the largest number whose square is less than or equal to 5. In this case, it is 2.
- Subtract \( 2^2 = 4 \) from 5 to get 1.00. Bring down a pair of zeros to make it 100.
- Double the quotient (2) to get 4. Determine a digit \( x \) such that \( 4x \times x \leq 100 \). The digit is 2, as \( 42 \times 2 = 84 \).
- Continue this process to refine the value to as many decimal places as needed.
Understanding \( \sqrt{5} \) helps in various mathematical applications, such as solving quadratic equations and analyzing geometric properties. For instance, \( \sqrt{5} \) appears in the Pythagorean theorem when dealing with right triangles having side lengths in the ratio 1:2. This demonstrates the square root of 5 as the diagonal of a rectangle with sides 1 and 2.
Simplifying Square Roots
Simplifying square roots involves expressing the square root in its simplest form. This process can make it easier to work with the number in various mathematical contexts. Here are the steps to simplify square roots:
Basic Rule
To simplify a square root, we use the property that . This means we can break down the number inside the square root into its prime factors and then simplify.
Step-by-Step Example
Let's simplify :
- Factor 45 into its prime factors: .
- Recognize that 9 is a perfect square: .
- Rewrite the square root using these factors: .
- Simplify the square roots: , so .
Additional Examples
- (since 72 = 36 × 2 and ).
- (since 50 = 25 × 2 and ).
- (since 8 = 4 × 2 and ).
By following these steps, you can simplify any square root to its most basic form, making it easier to work with in further calculations.
Step-by-Step Guide to Simplify the Square Root of 5
Simplifying the square root of 5 involves understanding the principles of radical expressions. Here is a comprehensive step-by-step guide to help you simplify square roots effectively:
-
Identify the Square Root:
Determine the number under the square root sign. In this case, it is \( \sqrt{5} \).
-
Prime Factorization (If Applicable):
Break down the number into its prime factors. Since 5 is already a prime number, this step is simplified for \( \sqrt{5} \).
-
Simplify Radical Expressions:
For numbers that can be simplified (unlike 5, which is prime), separate the number into its prime factors and simplify the square root by pairing identical factors. Extract paired factors outside the radical sign.
Since 5 is prime, it cannot be simplified further. Thus, \( \sqrt{5} \) remains \( \sqrt{5} \).
-
Decimal Approximation:
For practical purposes, you might need a decimal approximation. The approximate value of \( \sqrt{5} \) is 2.236.
To find this, you can use a calculator or the long division method for greater precision:
\( \sqrt{5} \approx 2.236 \) -
Using Rationalization Techniques:
In cases where you need to rationalize a denominator containing a square root, multiply the numerator and the denominator by the conjugate of the denominator to simplify.
For example, to rationalize \( \frac{1}{\sqrt{5}} \):
- Multiply by \( \frac{\sqrt{5}}{\sqrt{5}} \):
- \( \frac{1}{\sqrt{5}} \times \frac{\sqrt{5}}{\sqrt{5}} = \frac{\sqrt{5}}{5} \)
Following these steps ensures you understand the process of simplifying square roots, even if the specific square root, such as \( \sqrt{5} \), cannot be simplified further. The knowledge of these principles is crucial for handling various types of square roots in mathematical problems.

Properties of the Square Root of 5
The square root of 5, denoted as \( \sqrt{5} \), has several interesting properties and characteristics. Understanding these properties can provide deeper insights into its mathematical significance and applications.
- Real and Irrational: \( \sqrt{5} \) is a real number but not a rational number, meaning it cannot be expressed as a simple fraction. Instead, it is an irrational number with a non-repeating, non-terminating decimal expansion. The approximate value of \( \sqrt{5} \) is 2.23606.
- Positive and Negative Roots: Like any positive number, the square root of 5 has two roots: the positive root (\( \sqrt{5} \)) and the negative root (\( -\sqrt{5} \)). However, when we refer to "the square root of 5" in most contexts, we mean the principal (positive) root.
- Radical Form: The expression \( \sqrt{5} \) is in its simplest radical form. It cannot be simplified further because 5 is a prime number and not a perfect square.
- Exponential Form: The square root of 5 can also be expressed using exponents: \( 5^{1/2} \). This notation is often useful in higher mathematics, particularly in calculus and algebra.
- Geometric Interpretation: In geometry, \( \sqrt{5} \) represents the length of the diagonal of a rectangle with sides of length 1 and 2, based on the Pythagorean theorem. This provides a visual and practical understanding of its value.
- Algebraic Properties:
- Multiplicative Property: \( \sqrt{a} \times \sqrt{b} = \sqrt{a \cdot b} \). For example, \( \sqrt{5} \times \sqrt{20} = \sqrt{100} = 10 \).
- Division Property: \( \frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}} \). For instance, \( \frac{\sqrt{50}}{\sqrt{2}} = \sqrt{25} = 5 \).
- Applications: The square root of 5 appears in various mathematical and scientific contexts, including quadratic equations, physics problems, and more. Its properties make it a critical component in solving certain types of equations and understanding the behavior of mathematical functions.
Decimal Approximation of the Square Root of 5
The square root of 5 is an irrational number, which means it cannot be expressed as a simple fraction and its decimal representation is non-terminating and non-repeating. The decimal approximation of the square root of 5 can be calculated using various methods. Below is a detailed explanation of how to approximate the square root of 5 using different approaches.
Using a Calculator
One of the simplest ways to find the decimal approximation of the square root of 5 is by using a calculator. Enter the number 5 and press the square root (√) button. The calculator will display an approximate value:
√5 ≈ 2.23606797749979...
Using the Long Division Method
The long division method allows us to manually approximate the square root of a number to several decimal places. Here are the steps to approximate √5 using this method:
- Start with a pair of zeros after the decimal point (5.000000...).
- Find the largest number whose square is less than or equal to the first digit (in this case, 2, because 22 = 4).
- Subtract the square of this number from the first digit (5 - 4 = 1) and bring down a pair of zeros (100).
- Double the divisor (2 becomes 4) and find a new digit that fits (42 × 2 ≤ 100).
- Continue the process to get more decimal places.
Following these steps, the long division method approximates √5 as 2.236...
Using the Newton-Raphson Method
The Newton-Raphson method is an iterative numerical method to find successively better approximations of roots. The formula for the square root of 5 is:
\[ x_{n+1} = \frac{1}{2} \left( x_n + \frac{5}{x_n} \right) \]
Starting with an initial guess (e.g., \( x_0 = 2 \)), apply the formula iteratively:
- \( x_1 = \frac{1}{2} \left( 2 + \frac{5}{2} \right) = 2.25 \)
- \( x_2 = \frac{1}{2} \left( 2.25 + \frac{5}{2.25} \right) ≈ 2.236 \)
- Continue iterating until the desired accuracy is achieved.
Using this method, we quickly converge to the value 2.23606797749979...
Tabulated Decimal Values
Below is a table showing the decimal approximation of the square root of 5 to various decimal places:
| Decimal Places | Approximation |
|---|---|
| 1 | 2.2 |
| 2 | 2.24 |
| 3 | 2.236 |
| 4 | 2.2361 |
| 5 | 2.23607 |
| 6 | 2.236068 |
| 7 | 2.2360679 |
Conclusion
The decimal approximation of the square root of 5 is a crucial value in mathematics and engineering. Whether using a calculator, the long division method, or the Newton-Raphson method, we find that √5 ≈ 2.23606797749979... This value is used in various applications, including geometry, algebra, and real-world problem-solving.
Geometric Interpretation of the Square Root of 5
The square root of 5, denoted as \( \sqrt{5} \), can be interpreted geometrically using basic principles of Euclidean geometry. Here, we will explore a method to construct \( \sqrt{5} \) using a compass and straightedge, which provides a visual understanding of this irrational number.
Consider a right triangle construction to visualize \( \sqrt{5} \). Follow these steps:
-
Draw a horizontal line segment \( AB \) with length 2 units.
- Label the endpoints \( A \) and \( B \).
-
At point \( B \), draw a perpendicular line segment \( BC \) with length 1 unit.
- Label the endpoint of this segment as \( C \).
-
Connect points \( A \) and \( C \) with a straight line to form triangle \( ABC \).
-
Now, measure the length of the hypotenuse \( AC \) using the Pythagorean theorem:
\[
AC = \sqrt{AB^2 + BC^2} = \sqrt{2^2 + 1^2} = \sqrt{4 + 1} = \sqrt{5}
\]
Thus, the length of \( AC \) is \( \sqrt{5} \). This geometric construction shows that the hypotenuse of a right triangle with legs of lengths 2 and 1 units gives a length of \( \sqrt{5} \) units.
We can generalize this method to understand how other square roots can be constructed and visualized geometrically. The ability to construct such lengths using basic geometric tools emphasizes the elegance and utility of classical geometry in understanding irrational numbers.
Below is a table summarizing the construction steps:
| Step | Action | Result |
|---|---|---|
| 1 | Draw line segment \( AB \) (2 units) | \( AB = 2 \) units |
| 2 | Draw perpendicular \( BC \) at \( B \) (1 unit) | \( BC = 1 \) unit |
| 3 | Connect \( A \) and \( C \) | Right triangle \( ABC \) with hypotenuse \( AC \) |
| 4 | Calculate \( AC \) | \( AC = \sqrt{5} \) units |
This geometric interpretation helps us see how the square root of a number, such as 5, can be represented and constructed visually, providing a deeper appreciation for the connections between algebra and geometry.
Using Long Division Method to Calculate Square Roots
The long division method is a systematic way to find the square root of a number, particularly useful for non-perfect squares. Here, we will use the long division method to calculate the square root of 5. Follow the steps below to understand the process in detail:
-
Write the number 5 as 5.00000000 to ensure we have enough decimal places to work with.
-
Find the largest square number less than or equal to 5. This is 4 (since 22 = 4). Write 2 as the first digit of the quotient and also as the divisor.
-
Subtract 4 from 5 to get 1. Bring down two zeros to make it 100.
-
Double the quotient (2) to get 4 and write it down as the beginning of the new divisor.
-
Find a number (let's call it X) such that when it is placed next to 4 (forming 4X) and multiplied by X, the product is less than or equal to 100. Here, X = 2 (since 42 * 2 = 84). Write this 2 next to the quotient and subtract 84 from 100 to get 16.
-
Bring down the next pair of zeros, making the new number 1600. The current quotient is 2.2.
-
Double the current quotient (22) and write it as the beginning of the new divisor (44_).
-
Find a number Y such that 44Y * Y is less than or equal to 1600. Here, Y = 3 (since 443 * 3 = 1329). Subtract 1329 from 1600 to get 271.
-
Bring down the next pair of zeros, making the new number 27100. The current quotient is 2.23.
-
Double the current quotient (223) and write it as the beginning of the new divisor (446_).
-
Find a number Z such that 446Z * Z is less than or equal to 27100. Here, Z = 6 (since 4466 * 6 = 26796). Subtract 26796 from 27100 to get 304.
-
Continue this process to the desired level of precision. After a few more steps, the quotient will approximate the square root of 5 as 2.2360...
Thus, the square root of 5 using the long division method is approximately \( \sqrt{5} = 2.2360 \) or roughly 2.24 to two decimal places.
This method can be continued to find more decimal places as needed. It's a reliable way to compute square roots for non-perfect squares.

Applications of the Square Root of 5 in Mathematics
The square root of 5, denoted as \(\sqrt{5}\), plays a significant role in various mathematical concepts and real-world applications. Here are some notable applications:
-
The Golden Ratio
The Golden Ratio, often represented by the Greek letter Phi (\(\Phi\)), is closely connected to \(\sqrt{5}\). The formula for the Golden Ratio is:
\[\Phi = \frac{1 + \sqrt{5}}{2}\]
This ratio appears in numerous geometric figures, such as the proportions of a regular pentagon, and is fundamental in art, architecture, and nature.
-
Geometry
In geometry, \(\sqrt{5}\) is used to calculate dimensions and proportions. For instance, the diagonal of a rectangle with sides 1 and 2 units can be determined using the Pythagorean theorem, resulting in \(\sqrt{5}\) units.
-
Physics
\(\sqrt{5}\) appears in physics equations, such as in calculating the magnitude of vectors and in certain gravitational formulas. For example, the time \( t \) it takes for an object to fall from a height \( h \) can be approximated using the formula:
\[t = \frac{\sqrt{h}}{4}\]
This highlights the practical use of square roots in motion and gravity calculations.
-
Architecture and Design
Architects and designers use the Golden Ratio, which involves \(\sqrt{5}\), to create aesthetically pleasing and structurally sound buildings. The ratio is used to determine the proportions of various elements, ensuring visual harmony.
-
Fibonacci Sequence
The Fibonacci sequence, a series of numbers where each number is the sum of the two preceding ones, is related to the Golden Ratio. The ratio of successive Fibonacci numbers approximates \(\Phi\) as the numbers increase, showcasing \(\sqrt{5}\) in the formula:
\[F(n) = \frac{1}{\sqrt{5}} \left( \Phi^n - (1-\Phi)^n \right)\]
These examples illustrate the diverse applications of \(\sqrt{5}\) in mathematics and its profound impact on various fields such as geometry, physics, art, architecture, and natural phenomena.
Common Questions and Answers about Square Roots
Understanding square roots can sometimes be challenging. Here are some common questions and answers to help clarify this mathematical concept:
- What is a square root?
The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 25 is 5, because 5 x 5 = 25.
- How do you simplify square roots?
Simplifying a square root involves expressing it in its simplest radical form. For example, to simplify √50, we find the factors of 50, which are 2 x 5 x 5. We can take the square root of 5 x 5 out of the radical, resulting in 5√2.
- Can all square roots be simplified?
No, not all square roots can be simplified. For instance, √7 cannot be simplified further because 7 is a prime number and does not have any perfect square factors other than 1.
- What are perfect squares?
Perfect squares are numbers that are the square of an integer. Examples include 1, 4, 9, 16, 25, etc. The square roots of perfect squares are always integers.
- What is the decimal approximation of square roots?
When a number is not a perfect square, its square root is an irrational number and can be approximated as a decimal. For example, the square root of 5 is approximately 2.236.
- How do you find the square root of a number using a calculator?
To find the square root using a calculator, you simply enter the number and press the square root function (√) button. This will give you the square root in decimal form.
- What is the long division method for finding square roots?
The long division method involves a step-by-step process to manually find the square root of a number. This method is useful for finding precise square root values without a calculator.
These questions cover the basics of square roots, from their definition to methods for simplifying and calculating them.
Practice Problems and Solutions
Practicing square root problems helps in understanding the concept better and enhancing problem-solving skills. Here are some practice problems along with detailed solutions for better understanding:
Problem 1: Simplifying Square Roots
Simplify the following square roots:
- \(\sqrt{50}\)
- \(\sqrt{72}\)
- \(\sqrt{98}\)
Solutions:
- \(\sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2}\)
- \(\sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2}\)
- \(\sqrt{98} = \sqrt{49 \times 2} = \sqrt{49} \times \sqrt{2} = 7\sqrt{2}\)
Problem 2: Finding Square Roots Using Prime Factorization
Find the square root of the following numbers using the prime factorization method:
- 144
- 400
- 729
Solutions:
- \(144 = 2^4 \times 3^2\), so \(\sqrt{144} = \sqrt{2^4 \times 3^2} = 2^2 \times 3 = 4 \times 3 = 12\)
- \(400 = 2^4 \times 5^2\), so \(\sqrt{400} = \sqrt{2^4 \times 5^2} = 2^2 \times 5 = 4 \times 5 = 20\)
- \(729 = 3^6\), so \(\sqrt{729} = \sqrt{3^6} = 3^3 = 27\)
Problem 3: Square Root by Long Division Method
Find the square root of 361 using the long division method:
Solution:
- Group the digits in pairs from right to left: 3|61.
- Find the largest number whose square is less than or equal to the first group (3). This is 1, since \(1^2 = 1\).
- Subtract 1 from 3 to get the remainder 2. Bring down the next pair (61) to get 261.
- Double the divisor (1) to get 2. Determine how many times 2 fits into the first part of the remainder (26) when the divisor is written as 2x. The number is 6, since \(26/4 = 6\).
- The new divisor is 26, and the quotient is 6. So, the complete divisor is 16, and we subtract \(16 \times 16 = 256\) from 261 to get 5.
- Bring down the next pair of zeros to get 500. The process continues similarly, but since 361 is a perfect square, we have no remainder, and the square root of 361 is 19.
Problem 4: Mixed Problems
Solve the following problems:
- Evaluate \(\sqrt{121}\)
- Is \(\sqrt{200}\) an integer? If not, simplify it.
- Find the square root of 2025 by prime factorization.
Solutions:
- \(\sqrt{121} = 11\)
- \(\sqrt{200} = \sqrt{4 \times 50} = 2\sqrt{50} = 2 \times 5\sqrt{2} = 10\sqrt{2}\)
- \(2025 = 3^4 \times 5^2\), so \(\sqrt{2025} = \sqrt{3^4 \times 5^2} = 3^2 \times 5 = 9 \times 5 = 45\)
By practicing these problems, you will become more proficient in handling square roots and related mathematical concepts.
Additional Resources and Tools
Understanding and simplifying square roots can be enhanced with a variety of resources and tools available online. Here are some useful tools and resources to help you with square roots, including the square root of 5:
- Online Calculators
-
: This tool allows you to calculate the square root of any number and provides step-by-step solutions.
-
: This calculator simplifies any square root to its simplest radical form and provides decimal approximations.
-
: Another reliable tool to calculate and simplify square roots.
-
- Interactive Tutorials and Videos
-
: Offers comprehensive video tutorials and practice exercises on simplifying square roots and understanding their properties.
-
: Provides detailed lessons on simplifying square roots and offers practice problems to enhance your understanding.
-
- Worksheets and Practice Problems
-
: Downloadable worksheets with practice problems on simplifying square roots and other related topics.
-
: Offers a variety of worksheets and educational resources to practice square roots and other math skills.
-
- Mathematical Software
-
: A powerful computational tool that provides detailed solutions and explanations for square root problems.
-
: Interactive mathematics software for learning and teaching, including tools for exploring square roots.
-
These resources and tools can greatly assist in mastering the concept of square roots, offering both theoretical knowledge and practical problem-solving skills.

Conclusion
The exploration of the square root of 5 has provided a comprehensive understanding of this irrational number. Throughout this guide, we have delved into various aspects of the square root of 5, from its basic properties to its applications in mathematics.
Here are the key takeaways:
- The square root of 5 is an irrational number, approximately equal to 2.236.
- Simplifying square roots involves breaking down the number under the square root into its prime factors. However, since 5 is a prime number, the square root of 5 remains √5.
- The decimal approximation method provides a useful way to understand the value of √5, which is essential in various mathematical calculations.
- Geometrically, √5 can be interpreted as the length of the diagonal of a rectangle with sides of length 1 and 2.
- Using methods such as the long division method helps in manually calculating square roots, reinforcing the understanding of the process.
- Understanding the properties of √5 and its applications in different mathematical contexts, such as in the Fibonacci sequence and the golden ratio, highlights its significance.
By studying the square root of 5, we not only enhance our mathematical skills but also appreciate the beauty of numbers and their interconnections. This journey through the square root of 5 equips us with valuable problem-solving techniques and deepens our comprehension of mathematical concepts.
We encourage further practice and exploration of square roots and their properties to solidify this knowledge. The practice problems and additional resources provided will aid in this continuous learning process.
Thank you for joining us on this mathematical journey. We hope this guide has been insightful and has sparked a greater interest in the fascinating world of numbers.
Đơn giản hóa căn bậc hai | Toán học cùng Thầy J
Đơn giản hóa căn bậc hai | Toán học cùng Thầy J
READ MORE:
Hướng dẫn cách tìm tích của căn bậc hai của hai số trong video này. Khám phá cách tính toán căn(5) và căn(50) cùng Thầy J!
Cách Tìm Tích của Căn Bậc Hai của Hai Số, Căn(5) . Căn(50)