Topic simplifying radical expressions worksheet with answers: Unlock the secrets of simplifying radical expressions with our comprehensive worksheet and answers. Designed for students and educators, this guide covers essential concepts, step-by-step instructions, and challenging practice problems. Enhance your understanding and master radicals with ease using our expertly crafted resources and detailed solutions.
Table of Content
- Simplifying Radical Expressions Worksheet with Answers
- Introduction
- Basic Concepts of Radicals
- Steps to Simplify Radical Expressions
- Identifying Perfect Squares
- Factorization Techniques
- Simplifying Radicals with Fractions
- Practice Problems
- Model Problems with Solutions
- Challenge Problems
- Answer Key
- Common Mistakes and Tips
- YOUTUBE: Video hướng dẫn đơn giản hóa căn thức với biến số, số mũ, phân số và căn bậc ba. Phù hợp cho học sinh và giáo viên muốn hiểu rõ hơn về căn thức trong đại số.
Simplifying Radical Expressions Worksheet with Answers
Radical expressions can be simplified by identifying and extracting perfect square factors. This worksheet provides various problems for practice and mastery.
Worksheet Overview
- Objective: Practice simplifying radicals, focusing on Algebra 1 problems using real numbers.
- Structure: 25 scaffolded questions starting with basic problems and progressing to more challenging ones.
- Sections:
- Model Problems
- Practice Problems
- Challenge Problems
- Answer Key
Example Problems
- Simplify \( \sqrt{16} \)
- Simplify \( 3\sqrt{25} \)
- Simplify \( \sqrt{\frac{4}{121}} \)
Instructions
For each problem, follow these steps:
- Identify if the radicand (number under the radical) has a perfect square factor.
- Extract the perfect square factor and simplify.
- If no perfect square factor exists, simplify the expression by breaking it down into its prime factors.
Sample Problems and Solutions
| Problem | Solution |
|---|---|
| \( \sqrt{50} \) | \( \sqrt{25 \times 2} = 5\sqrt{2} \) |
| \( \sqrt{\frac{16}{49}} \) | \( \frac{\sqrt{16}}{\sqrt{49}} = \frac{4}{7} \) |
| \( 2\sqrt{18} \) | \( 2\sqrt{9 \times 2} = 2 \times 3\sqrt{2} = 6\sqrt{2} \) |
Additional Resources
For further practice and detailed explanations, check out the following resources:

READ MORE:
Introduction
Understanding how to simplify radical expressions is a fundamental skill in algebra that allows students to break down complex expressions into their simplest forms. This process involves identifying perfect squares within the radicand and factoring them out of the radical. By mastering this skill, students can solve equations more efficiently and gain a deeper understanding of mathematical relationships.
In this section, we will introduce the basic concepts and techniques for simplifying radical expressions. We will start with simple examples to illustrate the steps and gradually move on to more challenging problems. This approach will help students build confidence and develop a solid foundation in working with radicals.
- Definition of Radicals: Understanding the radicand and the index.
- Identifying Perfect Squares: Recognizing perfect squares up to 144.
- Simplifying Radicals: Step-by-step process for breaking down the radicand.
- Factoring Radicands: Techniques for factoring numbers within radicals.
- Combining Like Terms: Simplifying expressions with multiple radicals.
- Practice Problems: Examples and exercises to reinforce learning.
By the end of this section, students will be equipped with the knowledge and skills to simplify a wide range of radical expressions, preparing them for more advanced topics in algebra and beyond.
Basic Concepts of Radicals
Understanding the basic concepts of radicals is essential for simplifying radical expressions effectively. This section will guide you through the fundamental principles and terminologies associated with radicals.
A radical expression involves a root symbol (√) and a radicand, which is the number or expression inside the root symbol. The index, a small number placed to the upper left of the root symbol, indicates the degree of the root. For instance, the cube root of a number is denoted as .
- Square Roots: The most common type of radical. The square root of a number is a value that, when multiplied by itself, gives the original number. For example, √16 = 4 because 4 × 4 = 16.
- Cubic Roots: The cube root of a number is a value that, when used three times in a multiplication, gives the original number. For example, ∛27 = 3 because 3 × 3 × 3 = 27.
To simplify radicals, identify perfect squares or cubes within the radicand. For example, to simplify √50:
- Factor the radicand into its prime factors: 50 = 2 × 5²
- Separate the factors: √(2 × 5²) = √2 × √5²
- Simplify the perfect square: √2 × 5 = 5√2
By understanding and applying these basic concepts, you can simplify any radical expression systematically and accurately.
Steps to Simplify Radical Expressions
Simplifying radical expressions involves a systematic approach to ensure that the expression is in its simplest form. Here are the steps to follow:
- Identify the radicand: The radicand is the number or expression inside the radical symbol. For example, in , 50 is the radicand.
- Factor the radicand: Break down the radicand into its prime factors. For instance, 50 can be factored into 2 and 25.
- Pair the factors: Group the prime factors into pairs. Each pair of factors can be moved outside the radical. For example, can be written as .
- Simplify the pairs: For each pair of factors, move one of the factors outside the radical. In the example, becomes 5, so simplifies to .
- Simplify any remaining factors: If there are any factors left inside the radical that cannot be paired, they remain under the radical symbol. In the example, 2 remains under the radical.
By following these steps, you can simplify any radical expression efficiently and accurately.
Identifying Perfect Squares
Perfect squares are numbers that are the square of an integer. Recognizing these can simplify the process of working with radical expressions. Here’s how to identify perfect squares:
- List the squares of integers from 1 to 10:
- 12 = 1
- 22 = 4
- 32 = 9
- 42 = 16
- 52 = 25
- 62 = 36
- 72 = 49
- 82 = 64
- 92 = 81
- 102 = 100
- To check if a number is a perfect square, find the square root and determine if it is an integer.
- Example: 64 is a perfect square because √64 = 8.
- Use perfect squares to simplify radicals by factoring them out of the radical.
Identifying and using perfect squares can greatly simplify the process of working with radicals.

Factorization Techniques
Factorization is a key method in simplifying radical expressions. Here are some step-by-step techniques:
- Identify Perfect Squares: Look for perfect square factors in the radicand. For example, in \( \sqrt{50} \), the number 25 is a perfect square factor.
- Apply the Product Rule: Use the property \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \) to break down the expression. For \( \sqrt{50} \), this becomes \( \sqrt{25 \cdot 2} = \sqrt{25} \cdot \sqrt{2} \).
- Simplify: Simplify the square roots of perfect squares. In our example, \( \sqrt{25} = 5 \), so \( \sqrt{50} = 5\sqrt{2} \).
- Check for Further Simplification: Ensure the remaining radicand cannot be factored further into perfect squares. If not, the expression is fully simplified.
Using these techniques, you can simplify radical expressions efficiently, ensuring the radicand is minimized for simplicity.
Simplifying Radicals with Fractions
When simplifying radicals that involve fractions, we apply the quotient property, which allows us to simplify the numerator and denominator separately. Here's a step-by-step guide:
-
Separate the Radicals: Rewrite the expression by separating the radical in the numerator and the denominator. For example:
\(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
-
Simplify Each Part: Simplify the radicals in the numerator and denominator individually, looking for perfect squares or other factors.
- Example: \(\sqrt{\frac{25}{4}} = \frac{\sqrt{25}}{\sqrt{4}} = \frac{5}{2}\)
-
Rationalize the Denominator (if necessary): If the denominator is a radical, multiply the numerator and the denominator by a suitable radical to eliminate the radical in the denominator.
- Example: \(\frac{1}{\sqrt{2}} = \frac{1 \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}} = \frac{\sqrt{2}}{2}\)
Following these steps will help simplify any radical expression involving fractions effectively.
Practice Problems
Here are some practice problems to help you master simplifying radical expressions:
- Simplify \( \sqrt{50} \).
- Simplify \( \sqrt{72} \).
- Simplify \( \frac{\sqrt{45}}{\sqrt{5}} \).
- Simplify \( \sqrt{\frac{81}{16}} \).
- Simplify \( 3\sqrt{12} - 2\sqrt{27} \).
Try to solve these problems step-by-step. First, identify any perfect squares, then factorize the numbers under the radicals, and finally simplify the expressions.
Check your answers with the solution guide provided in the answer key section.
Model Problems with Solutions
In this section, we will work through several model problems to demonstrate the process of simplifying radical expressions. Each problem will be broken down step-by-step to ensure understanding.
-
Problem 1: Simplify \(\sqrt{50}\)
- Identify the factors of 50: \(50 = 25 \times 2\)
- Recognize that 25 is a perfect square: \(25 = 5^2\)
- Rewrite the radical: \(\sqrt{50} = \sqrt{25 \times 2}\)
- Separate the factors under the radical: \(\sqrt{25} \times \sqrt{2}\)
- Simplify: \(5\sqrt{2}\)
Solution: \(\sqrt{50} = 5\sqrt{2}\)
-
Problem 2: Simplify \(\sqrt{72}\)
- Identify the factors of 72: \(72 = 36 \times 2\)
- Recognize that 36 is a perfect square: \(36 = 6^2\)
- Rewrite the radical: \(\sqrt{72} = \sqrt{36 \times 2}\)
- Separate the factors under the radical: \(\sqrt{36} \times \sqrt{2}\)
- Simplify: \(6\sqrt{2}\)
Solution: \(\sqrt{72} = 6\sqrt{2}\)
-
Problem 3: Simplify \(\sqrt{18}\)
- Identify the factors of 18: \(18 = 9 \times 2\)
- Recognize that 9 is a perfect square: \(9 = 3^2\)
- Rewrite the radical: \(\sqrt{18} = \sqrt{9 \times 2}\)
- Separate the factors under the radical: \(\sqrt{9} \times \sqrt{2}\)
- Simplify: \(3\sqrt{2}\)
Solution: \(\sqrt{18} = 3\sqrt{2}\)
-
Problem 4: Simplify \(\frac{\sqrt{50}}{\sqrt{2}}\)
- Use the property of radicals: \(\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}\)
- Rewrite the expression: \(\frac{\sqrt{50}}{\sqrt{2}} = \sqrt{\frac{50}{2}}\)
- Simplify the fraction under the radical: \(\sqrt{25}\)
- Simplify the square root: \(5\)
Solution: \(\frac{\sqrt{50}}{\sqrt{2}} = 5\)
-
Problem 5: Simplify \(\sqrt{\frac{32}{8}}\)
- Simplify the fraction under the radical: \(\sqrt{4}\)
- Simplify the square root: \(2\)
Solution: \(\sqrt{\frac{32}{8}} = 2\)
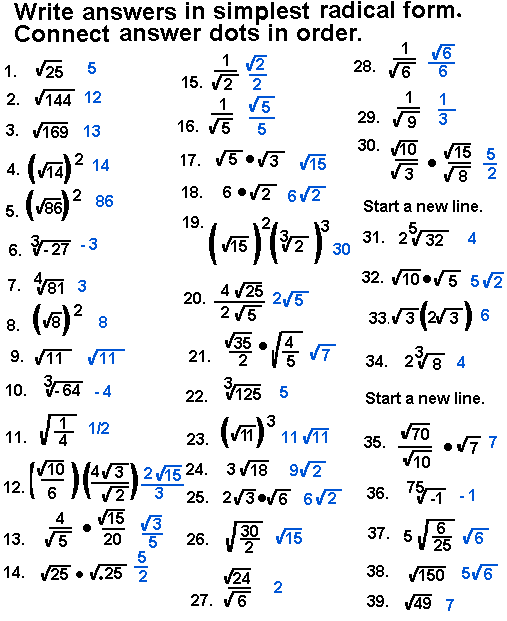
Challenge Problems
Below are some challenging problems involving simplifying radical expressions. Each problem requires careful attention to detail and application of multiple radical simplification rules. Solutions are provided to help you verify your answers and understand the steps involved.
-
Simplify: \( \sqrt{50} + 3\sqrt{2} \)
Solution:
\(\sqrt{50}\) can be simplified as follows:
\( \sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2} \)
Thus,
\( 5\sqrt{2} + 3\sqrt{2} = (5 + 3)\sqrt{2} = 8\sqrt{2} \)
-
Simplify: \( \sqrt{12} \times \sqrt{18} \)
Solution:
\(\sqrt{12} = \sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3} = 2\sqrt{3}\)
\(\sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} = 3\sqrt{2}\)
So,
\( \sqrt{12} \times \sqrt{18} = (2\sqrt{3}) \times (3\sqrt{2}) = 6\sqrt{6} \)
-
Simplify: \( \frac{\sqrt{75}}{\sqrt{3}} \)
Solution:
\( \frac{\sqrt{75}}{\sqrt{3}} = \sqrt{\frac{75}{3}} = \sqrt{25} = 5 \)
-
Simplify: \( \sqrt[3]{27x^6} \)
Solution:
\(\sqrt[3]{27x^6} = \sqrt[3]{27} \times \sqrt[3]{x^6} = 3 \times x^2 = 3x^2\)
-
Simplify: \( \sqrt[4]{16y^8} \)
Solution:
\(\sqrt[4]{16y^8} = \sqrt[4]{16} \times \sqrt[4]{y^8} = 2 \times y^2 = 2y^2\)
-
Simplify: \( \sqrt{8} \times \sqrt{2} + \sqrt{18} \)
Solution:
\(\sqrt{8} = \sqrt{4 \times 2} = 2\sqrt{2}\)
So, \( \sqrt{8} \times \sqrt{2} = 2\sqrt{2} \times \sqrt{2} = 2 \times 2 = 4 \)
\(\sqrt{18} = \sqrt{9 \times 2} = 3\sqrt{2}\)
Therefore, \( 4 + 3\sqrt{2} = 4 + 3\sqrt{2} \)
Answer Key
Here are the answers to the practice problems for simplifying radical expressions:
- √50 = 5√2
- √75 = 5√3
- √32 = 4√2
- √72 = 6√2
- √18 = 3√2
- √45 = 3√5
- √80 = 4√5
- √98 = 7√2
- √200 = 10√2
- √150 = 5√6
Below are the steps to simplify each expression:
-
√50
- Factor 50 into 25 and 2.
- √50 = √(25×2)
- Separate the factors: √25 × √2
- √25 = 5, so √50 = 5√2
-
√75
- Factor 75 into 25 and 3.
- √75 = √(25×3)
- Separate the factors: √25 × √3
- √25 = 5, so √75 = 5√3
-
√32
- Factor 32 into 16 and 2.
- √32 = √(16×2)
- Separate the factors: √16 × √2
- √16 = 4, so √32 = 4√2
-
√72
- Factor 72 into 36 and 2.
- √72 = √(36×2)
- Separate the factors: √36 × √2
- √36 = 6, so √72 = 6√2
-
√18
- Factor 18 into 9 and 2.
- √18 = √(9×2)
- Separate the factors: √9 × √2
- √9 = 3, so √18 = 3√2
-
√45
- Factor 45 into 9 and 5.
- √45 = √(9×5)
- Separate the factors: √9 × √5
- √9 = 3, so √45 = 3√5
-
√80
- Factor 80 into 16 and 5.
- √80 = √(16×5)
- Separate the factors: √16 × √5
- √16 = 4, so √80 = 4√5
-
√98
- Factor 98 into 49 and 2.
- √98 = √(49×2)
- Separate the factors: √49 × √2
- √49 = 7, so √98 = 7√2
-
√200
- Factor 200 into 100 and 2.
- √200 = √(100×2)
- Separate the factors: √100 × √2
- √100 = 10, so √200 = 10√2
-
√150
- Factor 150 into 25 and 6.
- √150 = √(25×6)
- Separate the factors: √25 × √6
- √25 = 5, so √150 = 5√6
Common Mistakes and Tips
Simplifying radical expressions can be challenging, and students often make common mistakes. Here are some frequent errors and tips to avoid them:
-
Mistake: Incorrectly identifying the radicand.
Tip: Ensure you correctly identify the radicand (the number under the radical sign). For example, in , the radicand is 27, not 3.
-
Mistake: Forgetting to factor out all perfect squares.
Tip: Always factor the radicand completely to find all perfect squares. For instance, should be simplified by recognizing that 72 = 36 * 2, thus .
-
Mistake: Ignoring negative signs under the radical.
Tip: Remember that the square root of a negative number involves imaginary numbers. For example, , not just 3.
-
Mistake: Incorrectly simplifying fractions inside radicals.
Tip: Simplify the fraction first if possible. For example, .
-
Mistake: Not rationalizing the denominator.
Tip: Always rationalize the denominator by multiplying by the conjugate if necessary. For example, .
-
Mistake: Combining unlike radicals.
Tip: Only combine like radicals. For instance, , but cannot be simplified further.
By being mindful of these common mistakes and following the tips provided, students can improve their skills in simplifying radical expressions.
Video hướng dẫn đơn giản hóa căn thức với biến số, số mũ, phân số và căn bậc ba. Phù hợp cho học sinh và giáo viên muốn hiểu rõ hơn về căn thức trong đại số.
Đơn Giản Hóa Căn Thức Với Biến Số, Số Mũ, Phân Số, Căn Bậc Ba - Đại Số
READ MORE:
Video hướng dẫn cách đơn giản hóa căn thức để thu hút người xem và chính tả chính xác.
Làm Thế Nào Để Đơn Giản Hóa Căn Thức