Topic simplifying a radical expression calculator: Discover the most effective ways to simplify radical expressions using our comprehensive calculator guide. This article breaks down complex radical expressions into simpler terms, making it easier for you to solve and understand these mathematical challenges. With step-by-step instructions and examples, you'll master radical simplification in no time!
Table of Content
- Simplifying Radical Expressions
- Introduction to Radical Expressions
- What is a Radical Expression?
- Basic Properties of Radicals
- Prime Factorization Method
- Product and Quotient Rules
- Rationalizing the Denominator
- Adding and Subtracting Radical Expressions
- Multiplying and Dividing Radical Expressions
- Simplifying Higher Order Roots
- Step-by-Step Calculator Usage
- Common Mistakes to Avoid
- Practice Problems
- Advanced Simplification Techniques
- Applications in Geometry and Algebra
- Additional Resources and Tools
- YOUTUBE: Video hướng dẫn sử dụng máy tính ClassWiz trong việc đơn giản hóa căn thức, phù hợp cho học sinh và giáo viên.
Simplifying Radical Expressions
Radical expressions can often be simplified using specific rules and methods. This process involves breaking down the radicand into its prime factors and simplifying the expression as much as possible.
Using a Simplifying Radical Expressions Calculator
There are various online calculators available to help simplify radical expressions. These calculators typically allow users to input values and perform operations such as addition, multiplication, and division on radical expressions.
- Calculators can handle square roots, cube roots, and other types of radicals.
- They often provide step-by-step solutions, making it easier to understand the process of simplification.
- Some calculators also offer additional features like prime factorization and rationalizing denominators.
Example Calculations
-
Simplifying \( \sqrt{75} + \sqrt{12} \):
\[
\sqrt{75} = \sqrt{25 \times 3} = 5\sqrt{3}, \quad \sqrt{12} = \sqrt{4 \times 3} = 2\sqrt{3}
\]Result: \( 7\sqrt{3} \)
-
Product of \( \sqrt{18} \times \sqrt{14} \):
\[
\sqrt{18} = 3\sqrt{2}, \quad \sqrt{14} = \sqrt{14}
\]Result: \( 6\sqrt{7} \)
Rules to Simplify Radicals
- The radicand must be a non-negative number.
- The nth root must be greater than or equal to 2.
These rules ensure that the simplified form of the radical expression is correct and reduced to its simplest terms.

READ MORE:
Introduction to Radical Expressions
Radical expressions involve roots, such as square roots, cube roots, and higher-order roots. These expressions can often appear complex, but simplifying them can make calculations easier and more intuitive. Simplifying a radical expression typically involves expressing it in its simplest form, where no further simplification is possible.
To begin understanding radical expressions, it's essential to know some fundamental concepts:
- Radical Symbol: The radical symbol (√) indicates the root of a number. For example, √25 represents the square root of 25.
- Radicand: The number inside the radical symbol. In √25, the radicand is 25.
- Index: The small number outside and to the left of the radical symbol, indicating the root. If no index is shown, it is assumed to be 2 (a square root).
To simplify a radical expression, follow these steps:
- Factor the Radicand: Break down the number inside the radical into its prime factors. For example, to simplify √72, start by expressing 72 as 2 × 2 × 2 × 3 × 3.
- Group the Factors: Group the prime factors into pairs. Each pair of factors can be taken out of the radical. Using √72 again, group the factors as (2 × 2) and (3 × 3), leaving the single 2 inside.
- Simplify: For each pair, take one factor out of the radical. In our example, √72 simplifies to 2 × 3√2, or 6√2.
Additionally, there are some rules to keep in mind when working with radicals:
- The nth root must be 2 or greater.
- The radicand must be a non-negative number when dealing with real numbers.
Understanding and applying these principles will make working with radical expressions more manageable, whether you are adding, subtracting, multiplying, or dividing them.
What is a Radical Expression?
A radical expression is an expression that includes a radical symbol (√) with a radicand under it. The radicand can be a number, a variable, or both. Radical expressions are used to represent roots, such as square roots, cube roots, and higher-order roots.
For example:
- \(\sqrt{16}\) represents the square root of 16.
- \(\sqrt[3]{27}\) represents the cube root of 27.
- \(\sqrt[4]{81}\) represents the fourth root of 81.
Radical expressions can be simplified using various mathematical techniques, including prime factorization and properties of exponents. Simplifying these expressions often makes them easier to work with in equations and other mathematical operations.
Here are some common properties of radicals that are used in simplification:
- Product Property: \(\sqrt{a} \cdot \sqrt{b} = \sqrt{a \cdot b}\)
- Quotient Property: \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
- Power Property: \(\sqrt[n]{a^m} = a^{\frac{m}{n}}\)
To simplify a radical expression:
- Factor the radicand into its prime factors.
- Apply the product and quotient properties of radicals.
- Simplify the expression by combining like terms.
For example, to simplify \(\sqrt{50}\):
- Factor 50 into prime factors: \(50 = 2 \cdot 5^2\).
- Apply the product property: \(\sqrt{50} = \sqrt{2 \cdot 5^2}\).
- Simplify by taking the square root of \(5^2\): \(\sqrt{50} = 5\sqrt{2}\).
Understanding and simplifying radical expressions are essential skills in algebra and higher-level mathematics. Simplification helps in solving equations and understanding the relationships between different mathematical concepts.
Basic Properties of Radicals
Radicals have several important properties that can simplify complex expressions. Understanding these properties is key to working with radical expressions efficiently.
- Product Property: The square root of a product is equal to the product of the square roots. This is expressed as:
\(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\)
- Quotient Property: The square root of a quotient is equal to the quotient of the square roots. This is expressed as:
\(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
- Simplifying Radicals: A radical expression is in its simplest form when there are no more square roots, cube roots, etc., to extract and no radicals appear in the denominator of a fraction.
- Factor the radicand into its prime factors.
- Apply the product property to separate the radicand into individual radicals.
- Simplify each radical.
- Combining Like Radicals: Similar to combining like terms in algebra, you can combine like radicals by adding or subtracting them. For example:
\(3\sqrt{2} + 4\sqrt{2} = 7\sqrt{2}\)
- Rationalizing the Denominator: To rationalize the denominator, multiply both the numerator and the denominator by a radical that will eliminate the radical in the denominator.
For example, to rationalize \(\frac{1}{\sqrt{2}}\), multiply by \(\frac{\sqrt{2}}{\sqrt{2}}\) to get \(\frac{\sqrt{2}}{2}\).
| Expression | Step | Result |
| \(\sqrt{50}\) | Factor 50 into prime factors | \(\sqrt{2 \cdot 5^2}\) |
| \(\sqrt{2 \cdot 5^2}\) | Apply product property | \(\sqrt{2} \cdot \sqrt{5^2}\) |
| \(\sqrt{2} \cdot \sqrt{5^2}\) | Simplify | \(\sqrt{2} \cdot 5\) |
| \(\sqrt{2} \cdot 5\) | Combine | \(5\sqrt{2}\) |
Prime Factorization Method
The prime factorization method is an effective technique for simplifying radical expressions. This method involves breaking down the number under the radical sign (the radicand) into its prime factors. By identifying pairs of prime factors, we can simplify the expression. Here’s a step-by-step guide:
- Find the Prime Factors:
Determine the prime factors of the radicand. For example, to simplify \(\sqrt{72}\), we first find its prime factors:
\[
72 = 2 \times 2 \times 2 \times 3 \times 3
\] - Group the Prime Factors:
Group the prime factors into pairs. Each pair of prime factors will come out of the radical as a single number. For \(\sqrt{72}\):
\[
72 = 2^2 \times 3^2 \times 2 = (2 \times 3) \times \sqrt{2} = 6\sqrt{2}
\] - Simplify the Expression:
Multiply the numbers that come out of the radical and leave the remaining factors inside. In our example:
\[
\sqrt{72} = 6\sqrt{2}
\]
Let’s look at another example to illustrate the method further:
Example: Simplify \(\sqrt{180}\)
- Find the Prime Factors:
\[
180 = 2 \times 2 \times 3 \times 3 \times 5
\] - Group the Prime Factors:
\[
180 = (2^2 \times 3^2) \times 5 = (2 \times 3) \times \sqrt{5} = 6\sqrt{5}
\] - Simplify the Expression:
\[
\sqrt{180} = 6\sqrt{5}
\]
This method can be applied to more complex expressions as well, including those involving variables:
Example: Simplify \(\sqrt{54a^{10}b^{16}c^7}\)
- Find the Prime Factors:
For the numerical part: \(54 = 2 \times 3 \times 3 \times 3\)
For the variables:
\[
a^{10} = (a^5)^2, \quad b^{16} = (b^8)^2, \quad c^7 = c^6 \times c
\] - Group the Prime Factors:
\[
54a^{10}b^{16}c^7 = (3 \times 3 \times 3) \times (a^5)^2 \times (b^8)^2 \times c^6 \times c = 3 \times 3 \times 3 \times a^5 \times b^8 \times c^3 \times \sqrt{6c}
\] - Simplify the Expression:
\[
\sqrt{54a^{10}b^{16}c^7} = 3a^5b^8c^3\sqrt{6c}
\]
By using the prime factorization method, we can systematically simplify radical expressions, making them easier to understand and work with.
Product and Quotient Rules
When simplifying radical expressions, the product and quotient rules are essential tools. These rules help us break down complex radicals into simpler forms. Below are detailed steps and examples to illustrate the use of these rules.
Product Rule for Radicals
The product rule states that the radical of a product is the product of the radicals. Mathematically, this is expressed as:
\[
\sqrt[n]{a \cdot b} = \sqrt[n]{a} \cdot \sqrt[n]{b}
\]
For example, to simplify \(\sqrt{12}\):
- Identify the factors of 12 that include a perfect square. Here, 12 can be written as 4 \(\cdot\) 3.
- Apply the product rule: \(\sqrt{12} = \sqrt{4 \cdot 3} = \sqrt{4} \cdot \sqrt{3}\).
- Simplify: \(\sqrt{4} = 2\), so \(\sqrt{12} = 2\sqrt{3}\).
Quotient Rule for Radicals
The quotient rule states that the radical of a quotient is the quotient of the radicals. Mathematically, this is expressed as:
\[
\sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a}}{\sqrt[n]{b}}
\]
For example, to simplify \(\sqrt{\frac{50}{121}}\):
- Identify the prime factorizations of 50 and 121. Here, 50 = \(5^2 \cdot 2\) and 121 = \(11^2\).
- Apply the quotient rule: \(\sqrt{\frac{50}{121}} = \sqrt{\frac{5^2 \cdot 2}{11^2}} = \frac{\sqrt{5^2 \cdot 2}}{\sqrt{11^2}}\).
- Simplify: \(\sqrt{5^2} = 5\) and \(\sqrt{11^2} = 11\), so \(\frac{\sqrt{50}}{\sqrt{121}} = \frac{5\sqrt{2}}{11}\).
Examples
Here are more examples to demonstrate these rules:
- Example 1: Simplify \(\sqrt{45}\)
- Identify the factors: 45 = 9 \(\cdot\) 5.
- Apply the product rule: \(\sqrt{45} = \sqrt{9 \cdot 5} = \sqrt{9} \cdot \sqrt{5} = 3\sqrt{5}\).
- Example 2: Simplify \(\sqrt{\frac{32}{2}}\)
- Identify the quotient: \(\frac{32}{2} = 16\).
- Apply the quotient rule: \(\sqrt{\frac{32}{2}} = \sqrt{16} = 4\).
- Example 3: Simplify \(\sqrt[3]{24}\)
- Identify the factors: 24 = 8 \(\cdot\) 3.
- Apply the product rule: \(\sqrt[3]{24} = \sqrt[3]{8 \cdot 3} = \sqrt[3]{8} \cdot \sqrt[3]{3} = 2\sqrt[3]{3}\).
These examples illustrate how the product and quotient rules simplify radical expressions efficiently. By breaking down complex radicals into simpler components, calculations become more manageable and accurate.
Rationalizing the Denominator
Rationalizing the denominator is a technique used to eliminate radicals from the denominator of a fraction. This process involves multiplying the numerator and the denominator by a suitable radical that will simplify the denominator. Below are the steps and examples to rationalize denominators:
Steps to Rationalize the Denominator
- Identify the radical in the denominator.
- Multiply both the numerator and the denominator by a radical that will simplify the denominator into a rational number.
- Simplify the resulting expression if possible.
Examples
-
Example 1: Simplify \( \frac{1}{\sqrt{2}} \)
- Multiply by \( \frac{\sqrt{2}}{\sqrt{2}} \):
\( \frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2} \)
-
Example 2: Simplify \( \frac{3}{\sqrt{5}} \)
- Multiply by \( \frac{\sqrt{5}}{\sqrt{5}} \):
\( \frac{3}{\sqrt{5}} \times \frac{\sqrt{5}}{\sqrt{5}} = \frac{3\sqrt{5}}{5} \)
-
Example 3: Simplify \( \frac{4}{1 + \sqrt{3}} \)
- Multiply by the conjugate \( \frac{1 - \sqrt{3}}{1 - \sqrt{3}} \):
\( \frac{4}{1 + \sqrt{3}} \times \frac{1 - \sqrt{3}}{1 - \sqrt{3}} = \frac{4(1 - \sqrt{3})}{(1 + \sqrt{3})(1 - \sqrt{3})} = \frac{4 - 4\sqrt{3}}{1 - 3} = \frac{4 - 4\sqrt{3}}{-2} = -2 + 2\sqrt{3} \)
Why Rationalize the Denominator?
Rationalizing the denominator is often done to simplify expressions and to make them easier to understand and compare. It is particularly useful in geometry and algebra when dealing with lengths, areas, and other measurements involving radicals.
Practice Problems
- Rationalize the denominator of \( \frac{2}{\sqrt{3}} \)
- Rationalize the denominator of \( \frac{5}{2 + \sqrt{7}} \)
- Rationalize the denominator of \( \frac{6}{4 - \sqrt{10}} \)
Adding and Subtracting Radical Expressions
Adding and subtracting radical expressions involves combining like terms. For radicals to be considered like terms, they must have the same radicand (the number inside the radical) and the same index (the type of root, such as square root or cube root).
Here's how you can add or subtract radical expressions step by step:
Step-by-Step Process:
- Simplify Each Radical:
Before adding or subtracting, ensure each radical is in its simplest form. For example, simplify \(\sqrt{50}\) to \(5\sqrt{2}\).
- \(\sqrt{50} = \sqrt{25 \times 2} = 5\sqrt{2}\)
- \(\sqrt{18} = \sqrt{9 \times 2} = 3\sqrt{2}\)
- Identify Like Radicals:
Only like radicals can be combined. Like radicals have the same radicand and index.
Example:
- \(3\sqrt{2}\) and \(5\sqrt{2}\) are like radicals and can be added or subtracted.
- \(3\sqrt{2}\) and \(2\sqrt{3}\) are not like radicals and cannot be combined.
- Combine Like Terms:
Add or subtract the coefficients of like radicals. The radicand remains the same.
Example:
- \(3\sqrt{2} + 5\sqrt{2} = (3 + 5)\sqrt{2} = 8\sqrt{2}\)
- \(7\sqrt{3} - 2\sqrt{3} = (7 - 2)\sqrt{3} = 5\sqrt{3}\)
- Combine Different Radicals:
If radicals are not like terms, list them together without combining.
Example:
- \(3\sqrt{2} + 4\sqrt{3} = 3\sqrt{2} + 4\sqrt{3}\)
- \(5\sqrt{7} - \sqrt{3} = 5\sqrt{7} - \sqrt{3}\)
Examples:
Let's apply these steps to some examples:
- Example 1: Simplify \(2\sqrt{3} + 4\sqrt{3} - \sqrt{3}\)
Combine like terms:
- \((2 + 4 - 1)\sqrt{3} = 5\sqrt{3}\)
- Example 2: Simplify \(3\sqrt{5} - 2\sqrt{5} + 4\sqrt{2}\)
Combine like terms:
- \((3 - 2)\sqrt{5} = \sqrt{5}\)
- Since \(4\sqrt{2}\) is a different radical, it remains unchanged.
- The final result is: \(\sqrt{5} + 4\sqrt{2}\)
Adding and subtracting radical expressions can be simplified using these steps. Remember to always simplify each radical expression first and then combine like terms.
Multiplying and Dividing Radical Expressions
When multiplying and dividing radical expressions, it's important to understand the properties of radicals and how to apply them. Here are the steps and rules for performing these operations:
Multiplying Radical Expressions
To multiply radical expressions, you can use the following rule:
\[\sqrt{a} \cdot \sqrt{b} = \sqrt{a \cdot b}\]
Follow these steps:
- Multiply the numbers outside the radicals.
- Multiply the numbers inside the radicals.
- Simplify the resulting expression if possible.
Example:
\(\sqrt{3} \cdot \sqrt{12} = \sqrt{3 \cdot 12} = \sqrt{36} = 6\)
Dividing Radical Expressions
To divide radical expressions, use the following rule:
\[\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}\]
Follow these steps:
- Divide the numbers outside the radicals.
- Divide the numbers inside the radicals.
- Simplify the resulting expression if possible.
- If the denominator is a radical, rationalize it by multiplying the numerator and the denominator by the same radical to eliminate the radical in the denominator.
Example:
\(\frac{\sqrt{18}}{\sqrt{2}} = \sqrt{\frac{18}{2}} = \sqrt{9} = 3\)
To rationalize the denominator:
\(\frac{5}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{5\sqrt{2}}{2}\)
Practice Problems
- \(\sqrt{5} \cdot \sqrt{20}\)
- \(\frac{\sqrt{50}}{\sqrt{2}}\)
- \(\sqrt{7} \cdot \sqrt{14}\)
- \(\frac{6}{\sqrt{3}}\)
By following these steps and practicing with different problems, you'll become proficient at multiplying and dividing radical expressions. Remember to always simplify your final answers.

Simplifying Higher Order Roots
Simplifying higher order roots involves reducing expressions that contain radicals of any order, such as cube roots, fourth roots, and beyond. The process is similar to simplifying square roots but requires additional steps due to the higher order.
Step-by-Step Process
-
Prime Factorization: Begin by finding the prime factorization of the radicand (the number inside the radical). For example, for the cube root of 216, you first find that 216 = 23 × 33.
-
Group the Factors: Group the prime factors based on the order of the root. For a cube root, group the factors in sets of three. For example, 23 × 33 becomes (2 × 3)3.
-
Simplify the Radicand: Take out one factor from each group. In the example, (2 × 3)3 simplifies to 6, since (2 × 3) = 6.
-
Write the Simplified Expression: Combine the simplified radicand with any remaining factors inside the radical. For our example, the cube root of 216 simplifies to 6.
Examples
Example 1: Simplify \( \sqrt[3]{54} \)
Prime factorization of 54: 54 = 2 × 33
Grouping the factors for a cube root: \( \sqrt[3]{2 \times 3^3} \)
Simplified: 3 \( \sqrt[3]{2} \)
Example 2: Simplify \( \sqrt[4]{256} \)
Prime factorization of 256: 256 = 28
Grouping the factors for a fourth root: \( \sqrt[4]{(2^2)^4} \)
Simplified: 22 = 4
Special Considerations
Mixed Radicals: When simplifying expressions with mixed radicals, such as \( 2 \sqrt[3]{27} \), simplify each radical separately before combining them. For example, \( 2 \sqrt[3]{27} = 2 \times 3 = 6 \).
Rationalizing the Denominator: When the denominator of a fraction contains a higher-order root, multiply the numerator and denominator by a radical that will eliminate the root from the denominator.
Using Calculators
Various online calculators can assist with simplifying higher order roots by providing step-by-step solutions and verifying manual calculations. These tools are especially useful for complex expressions and checking your work.
Step-by-Step Calculator Usage
Simplifying radical expressions can be straightforward using an online calculator. Below are the steps to simplify a radical expression using a calculator:
- Open the Calculator: Navigate to a reliable online simplifying radical expressions calculator such as CalculatorSoup, MathPortal, or Calculators.Live.
- Input the Expression: Enter the radical expression you wish to simplify. Ensure you use the correct notation, for example,
\sqrt{50}or\sqrt[3]{27}. - Select the Operation: Choose the operation you want to perform, such as simplification, addition, subtraction, multiplication, or division of radicals.
- Execute the Calculation: Click the calculate button. The calculator will process the expression and display the simplified form.
Here are a few examples to illustrate the process:
Example 1: Simplifying \(\sqrt{50}\)
- Step 1: Enter \(\sqrt{50}\) in the input field.
- Step 2: Click on the simplify button.
- Result: The calculator shows \(\sqrt{50} = 5\sqrt{2}\).
Example 2: Adding Radicals \(\sqrt{75} + \sqrt{12}\)
- Step 1: Enter \(\sqrt{75} + \sqrt{12}\) in the input field.
- Step 2: Click on the calculate button.
- Result: The calculator shows \(5\sqrt{3} + 2\sqrt{3} = 7\sqrt{3}\).
Example 3: Multiplying Radicals \(\sqrt{18} \times \sqrt{14}\)
- Step 1: Enter \(\sqrt{18} \times \sqrt{14}\) in the input field.
- Step 2: Click on the calculate button.
- Result: The calculator shows \(\sqrt{18} \times \sqrt{14} = 6\sqrt{7}\).
These steps and examples should help you efficiently use online calculators to simplify radical expressions. Always ensure to double-check the results and understand the steps involved in the simplification process for better learning and application.
Common Mistakes to Avoid
When simplifying radical expressions, there are several common mistakes that students often make. Avoiding these errors can help ensure your solutions are correct and simplify the process effectively. Here are some key mistakes to watch out for:
- Incorrectly Applying the Product Rule: The product rule states that \(\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}\) for non-negative values of \(a\) and \(b\). Ensure that you only apply this rule when both \(a\) and \(b\) are non-negative.
- Not Fully Simplifying Radicands: Always look for the largest perfect square factor of the radicand. For example, simplifying \(\sqrt{72}\) should be done by recognizing \(72 = 36 \times 2\), giving \(\sqrt{72} = 6\sqrt{2}\). Smaller factors like \(4\) or \(9\) lead to more steps.
- Ignoring Absolute Values: When simplifying even roots, remember to use absolute values if the variable inside the radical could be negative. For example, \(\sqrt{x^2} = |x|\).
- Misidentifying Perfect Squares: Ensure you correctly identify perfect squares. For instance, rewriting \(\sqrt{48}\) as \(\sqrt{16 \times 3}\) is correct, while \(\sqrt{6 \times 8}\) is not helpful.
- Overlooking Prime Factorization: Use prime factorization to simplify radicals with variables. For example, \(\sqrt{54a^{10}b^{16}c^7}\) simplifies to \(3a^5b^8c^3\sqrt{6c}\) by pairing and reducing exponents.
- Failing to Combine Like Terms: When adding or subtracting radical expressions, combine like terms. For instance, \(2\sqrt{3} + 3\sqrt{3} = 5\sqrt{3}\).
By being mindful of these common mistakes, you can improve your skills in simplifying radical expressions and avoid common pitfalls that lead to incorrect answers.
Practice Problems
Here are some practice problems to help you master the simplification of radical expressions. Work through each problem step-by-step to ensure you understand the process.
-
Simplify the following radical expressions:
- \(\sqrt{50}\)
- \(\sqrt{72}\)
- \(\sqrt{18}\)
-
Simplify the following expressions involving variables:
- \(\sqrt{75x^2}\)
- \(\sqrt{48y^3}\)
- \(\sqrt{20z^4}\)
-
Use the product rule of radicals to simplify:
- \(\sqrt{45 \cdot 20}\)
- \(\sqrt{12} \cdot \sqrt{3}\)
- \(\sqrt{8} \cdot \sqrt{2}\)
-
Simplify by rationalizing the denominator:
- \(\frac{5}{\sqrt{2}}\)
- \(\frac{7}{\sqrt{3}}\)
- \(\frac{4}{\sqrt{5}}\)
-
Simplify the following higher-order roots:
- \(\sqrt[3]{54}\)
- \(\sqrt[4]{81}\)
- \(\sqrt[5]{32}\)
-
Combine like terms and simplify:
- \(3\sqrt{2} + 2\sqrt{2}\)
- \(4\sqrt{3} - \sqrt{27}\)
- \(5\sqrt{5} + 2\sqrt{20}\)
-
Solve the following equations by simplifying radicals:
- \(\sqrt{x} = 4\)
- \(2\sqrt{y} = 10\)
- \(\sqrt{z} + 3 = 7\)
These problems cover a range of techniques including basic simplification, use of the product rule, rationalizing denominators, and combining like terms. Work through each problem carefully and check your answers with a calculator to ensure accuracy.

Advanced Simplification Techniques
Advanced simplification techniques for radical expressions involve several methods that go beyond basic rules. These techniques are essential for handling more complex expressions efficiently.
1. Using the Product Rule
The product rule for radicals states that \(\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}\). This rule can be extended to higher order roots:
\[\sqrt[n]{ab} = \sqrt[n]{a} \cdot \sqrt[n]{b}\]
Example:
\[\sqrt{50} = \sqrt{25 \cdot 2} = \sqrt{25} \cdot \sqrt{2} = 5\sqrt{2}\]
2. Using the Quotient Rule
The quotient rule for radicals is given by \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\). This helps simplify expressions involving division:
\[\sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a}}{\sqrt[n]{b}}\]
Example:
\[\sqrt{\frac{18}{2}} = \sqrt{9} = 3\]
3. Rationalizing the Denominator
Rationalizing the denominator involves eliminating radicals from the denominator of a fraction. This can be done by multiplying the numerator and the denominator by a suitable radical expression:
Example:
\[\frac{1}{\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}} = \frac{\sqrt{3}}{3}\]
4. Simplifying Higher Order Roots
Higher order roots can be simplified by expressing the radicand as a product of perfect powers:
Example:
\[\sqrt[3]{27x^3} = \sqrt[3]{3^3 \cdot x^3} = 3x\]
5. Prime Factorization
Prime factorization involves breaking down the radicand into its prime factors and then simplifying:
Example:
\[\sqrt{72} = \sqrt{2^3 \cdot 3^2} = 3\sqrt{8} = 3 \cdot 2\sqrt{2} = 6\sqrt{2}\]
6. Dealing with Variables
For expressions involving variables, ensure all variable exponents are even for square roots or multiples of the root index for higher order roots:
Example:
\[\sqrt{18x^3y^4} = \sqrt{2 \cdot 3^2 \cdot x^2 \cdot xy^4} = 3xy^2\sqrt{2x}\]
Practice and Application
Applying these techniques requires practice. Here are some problems to try:
- Simplify \(\sqrt{200}\).
- Simplify \(\sqrt[4]{81x^8}\).
- Rationalize the denominator of \(\frac{2}{\sqrt{5}}\).
- Simplify \(\sqrt[3]{54a^{10}b^{16}c^7}\).
Applications in Geometry and Algebra
Radical expressions frequently appear in geometry and algebra, providing a means to simplify complex problems. Understanding their applications can enhance problem-solving skills and deepen mathematical comprehension.
Geometry
- Distance Formula: The distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) in the coordinate plane is given by:
\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]
Simplifying this radical expression helps in quickly determining the distance. - Area of a Right Triangle: Given the legs \(a\) and \(b\) of a right triangle, the hypotenuse \(c\) is:
\[
c = \sqrt{a^2 + b^2}
\]
This is derived from the Pythagorean theorem and is crucial in many geometric calculations. - Circle Properties: The radius of a circle inscribed in a triangle can be found using the area \(A\) and the semi-perimeter \(s\):
\[
r = \frac{A}{s}
\]
Simplifying this expression is essential for accurate geometric constructions.
Algebra
- Simplifying Polynomial Equations: Radical expressions are used to simplify roots in polynomial equations, making it easier to solve them.
For example, to solve \(x^2 - 6x + 9 = 0\):
\[
x = \frac{6 \pm \sqrt{36 - 36}}{2} = \frac{6 \pm 0}{2} = 3
\]
Here, the radical expression \(\sqrt{36 - 36}\) is simplified to aid in finding the solution. - Quadratic Formula: The quadratic formula for solving \(ax^2 + bx + c = 0\) involves a radical expression:
\[
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\]
Simplifying the discriminant \(\sqrt{b^2 - 4ac}\) is a key step in determining the roots. - Exponential Equations: Radical expressions also appear when solving exponential equations through logarithms. For instance:
\[
2^x = 8 \implies x = \log_2(8) = \log_2(2^3) = 3
\]
Simplifying the expression inside the logarithm helps in finding the exponent \(x\).
Understanding and simplifying radical expressions are invaluable skills in geometry and algebra, facilitating a range of problem-solving techniques and mathematical insights.
Additional Resources and Tools
In this section, we explore various resources and tools available to aid in simplifying radical expressions. These resources provide step-by-step solutions, practice problems, and interactive calculators to help you master the topic.
Online Calculators
- Symbolab Calculator: This tool allows you to simplify radical expressions and provides detailed steps for solving. It supports various types of algebraic operations, making it a versatile resource for students.
- Calculator Soup: An easy-to-use calculator that simplifies radical expressions by showing the prime factorization and step-by-step solutions.
- MathPortal: This site offers a calculator that can simplify complex radical expressions, making it a great tool for tackling more challenging problems.
Educational Websites
- Khan Academy: Offers comprehensive lessons and practice exercises on simplifying radicals, including video tutorials to enhance understanding.
- MathIsFun: Provides clear explanations and interactive examples on simplifying radical expressions, ideal for visual learners.
Practice Problems
- IXL Learning: Features a wide range of practice problems that adapt to your skill level, helping reinforce your understanding of radical simplification.
- Wolfram Alpha: Not only can it solve radical expressions, but it also offers practice problems to test your skills.
Interactive Learning Tools
- GeoGebra: An interactive tool that helps visualize and simplify radical expressions, making abstract concepts more concrete.
- Desmos: Provides graphing tools and algebraic simplification features, which are useful for exploring and understanding radicals.
Books and Articles
- "Algebra for Dummies" by Mary Jane Sterling: A comprehensive guide that includes sections on simplifying radicals, with easy-to-understand explanations and examples.
- Articles on MathWorld: Detailed articles that cover the theory and practice of radical expressions, suitable for more advanced learners.
Mobile Apps
- Photomath: Allows you to take pictures of math problems and provides instant solutions with step-by-step explanations.
- Mathway: A powerful tool for solving various math problems, including simplifying radicals, available on both Android and iOS.
Video hướng dẫn sử dụng máy tính ClassWiz trong việc đơn giản hóa căn thức, phù hợp cho học sinh và giáo viên.
Hướng Dẫn Sử Dụng Máy Tính ClassWiz - Đại Số 4-1 Đơn Giản Hóa Căn Thức
READ MORE:
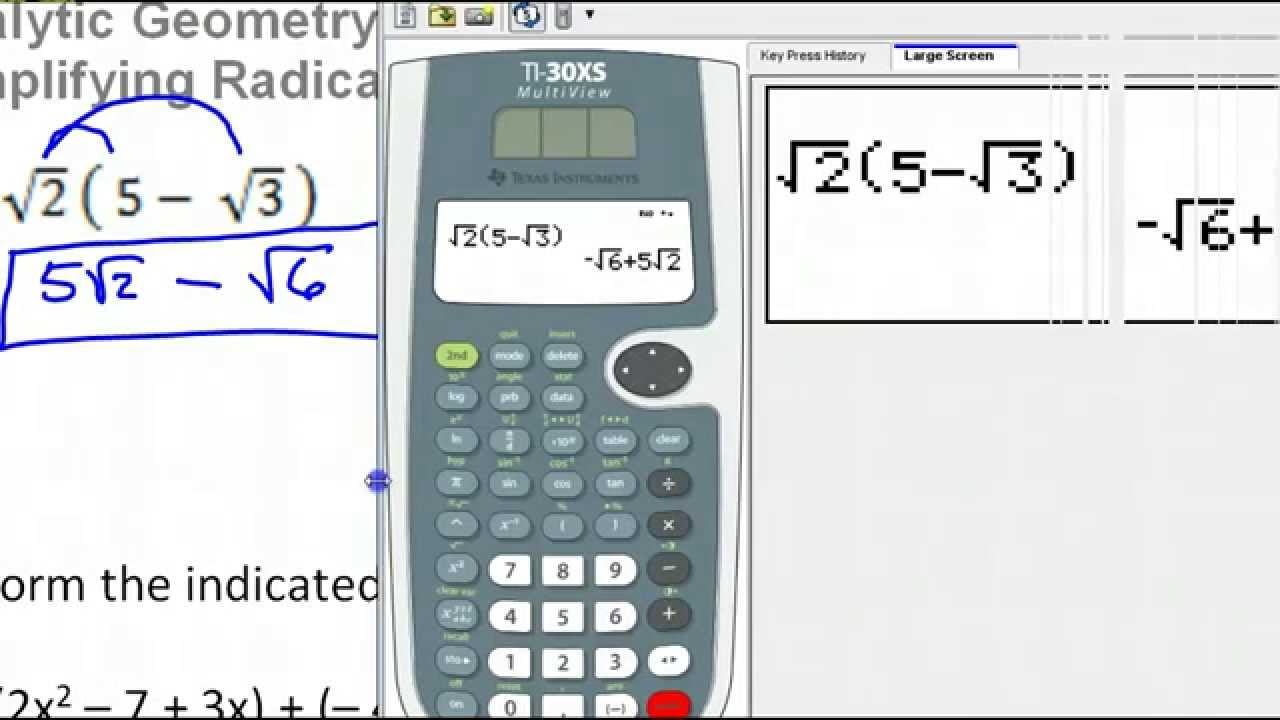
Video mẹo toán học hướng dẫn cách đơn giản hóa căn thức sử dụng máy tính TI-84 Plus, rất hữu ích cho học sinh và giáo viên.
Mẹo Toán Học - Đại Số Với TI-84 Plus - Đơn Giản Hóa Căn Thức