Topic simplify rational expressions calculator with steps: Discover the ease of simplifying rational expressions with our comprehensive guide. Our step-by-step calculator simplifies complex rational expressions effortlessly. Learn how to tackle algebraic fractions, reduce them to their simplest form, and understand each step in the process. Whether you’re a student or math enthusiast, this tool will enhance your mathematical skills.
Table of Content
- Simplify Rational Expressions Calculator with Steps
- Introduction to Rational Expressions
- What are Rational Expressions?
- How to Simplify Rational Expressions
- Steps for Simplifying Rational Expressions
- Operations on Rational Expressions
- Adding Rational Expressions
- Subtracting Rational Expressions
- Multiplying Rational Expressions
- Dividing Rational Expressions
- Examples and Solutions
- Using Online Calculators
- Common Mistakes and Tips
- Practice Problems
- Additional Resources
- FAQs
- YOUTUBE: Học cách vẽ đồ thị hàm số hữu tỉ qua 6 bước đơn giản và dễ hiểu.
Simplify Rational Expressions Calculator with Steps
Simplifying rational expressions can be made easier with the use of online calculators that provide step-by-step solutions. These calculators help in breaking down complex expressions into simpler forms, making it easier to understand and solve them. Below are some key features and examples of how these calculators work.
Features of Simplify Rational Expressions Calculators
- Step-by-step explanations for each stage of simplification.
- Ability to handle complex fractions and polynomial expressions.
- Support for various algebraic functions and operations.
- Interactive user interface for easy input of expressions.
- Graphical representations of simplified expressions.
Examples
Here are a few examples of how to simplify rational expressions using these calculators:
-
Given the rational expression:
\[
\frac{6x^2 - 12x}{3x}
\]The calculator will simplify it step-by-step as follows:
- Factor the numerator: \(6x^2 - 12x = 6x(x - 2)\)
- Rewrite the expression: \(\frac{6x(x - 2)}{3x}\)
- Cancel the common factor \(3x\): \(2(x - 2)\)
- Final simplified form: \(2(x - 2)\)
-
\[
\frac{x^2 + 2x - 3}{x^2 - 1}
\]- Factor the numerator: \(x^2 + 2x - 3 = (x + 3)(x - 1)\)
- Factor the denominator: \(x^2 - 1 = (x + 1)(x - 1)\)
- Rewrite the expression: \(\frac{(x + 3)(x - 1)}{(x + 1)(x - 1)}\)
- Cancel the common factor \(x - 1\): \(\frac{x + 3}{x + 1}\)
- Final simplified form: \(\frac{x + 3}{x + 1}\)
Benefits
Using a simplify rational expressions calculator with steps provides several benefits:
- Enhances understanding of algebraic concepts through detailed solutions.
- Reduces the time spent on manual calculations.
- Helps verify the correctness of manual solutions.
- Supports learning by providing immediate feedback and explanations.
Conclusion
Simplifying rational expressions can be challenging, but with the help of online calculators, it becomes much more manageable. These tools offer comprehensive support, detailed step-by-step solutions, and interactive features to aid in the learning and solving process. Whether you are a student, teacher, or math enthusiast, a simplify rational expressions calculator with steps can be an invaluable resource.

READ MORE:
Introduction to Rational Expressions
Rational expressions are algebraic expressions that can be expressed as the quotient of two polynomials. These expressions are important in algebra and higher mathematics because they allow for the manipulation and simplification of complex polynomial relationships.
A rational expression is generally written in the form:
\[ \dfrac{A(x)}{B(x)} \]
where \(A(x)\) and \(B(x)\) are polynomials and \(B(x) \neq 0\). The expression represents the division of one polynomial by another. For example:
\[ \dfrac{6x + 1}{2x + 1} \]
Simplifying rational expressions involves factoring the polynomials in the numerator and denominator and then canceling out common factors. Here are the basic steps:
- Factor both the numerator and the denominator.
- Identify and cancel common factors.
- Simplify the resulting expression.
Let's consider a few arithmetic operations that can be performed on rational expressions:
-
Addition
- Write all terms separately as a sum.
- Find the least common multiple (LCM) of the denominators.
- Add the numerators over the common denominator.
- Cancel like terms with opposite signs.
-
Subtraction
- Write all terms separately as a difference.
- Find the LCM of the denominators.
- Subtract the numerators over the common denominator.
- Cancel like terms with opposite signs.
-
Multiplication
- Multiply the numerators together and the denominators together.
- Apply the distributive property where needed.
- Simplify by canceling common factors.
-
Division
- Rewrite the division as multiplication by the reciprocal.
- Multiply the numerators and the denominators.
- Cancel common factors to simplify.
By understanding these basic operations and the structure of rational expressions, one can solve complex algebraic problems more efficiently.
What are Rational Expressions?
A rational expression is a fraction in which both the numerator and the denominator are polynomials. Rational expressions can be simple, like \( \frac{x+1}{x-1} \), or more complex, involving multiple terms and operations. The standard form of a rational expression is:
\[
Rational\ Expression = \frac{A(x)}{B(x)}
\]
where \( A(x) \) and \( B(x) \) are polynomials, and \( B(x) \neq 0 \).
To simplify a rational expression, the common factors in the numerator and denominator must be identified and canceled. Here are the key operations you can perform on rational expressions:
- Addition:
- Write all terms separately as a sum.
- Find the least common multiple (LCM) of the denominators.
- Add the numerators over the common denominator.
- Cancel like terms with opposite signs to simplify.
- Subtraction:
- Write all terms separately as a subtraction.
- Take the LCM for a common denominator.
- Subtract the numerators over the common denominator.
- Cancel like terms with opposite signs to simplify.
- Multiplication:
- Multiply the numerators and denominators separately.
- Apply the distributive property to simplify.
- Add and subtract terms accordingly.
- Rewrite the expression in descending order of powers.
- Division:
- Write the terms with a division sign.
- Take the reciprocal of the divisor and change the division sign to multiplication.
- Multiply the numerators and denominators separately.
- Cancel like terms with opposite signs to simplify.
Understanding these operations and following the steps carefully ensures that you can simplify any rational expression efficiently. Using a rational expressions calculator can further aid in performing these steps quickly and accurately, providing step-by-step solutions to enhance understanding.
How to Simplify Rational Expressions
To simplify rational expressions, follow these steps:
- Factor the Numerator and Denominator: Begin by factoring both the numerator and the denominator into their simplest forms. Look for common factors in both parts.
- Identify and Cancel Common Factors: Cancel out any common factors that appear in both the numerator and the denominator. This reduces the expression to its simplest form.
- Apply Arithmetic Operations: Perform any necessary addition, subtraction, multiplication, or division to further simplify the expression. Use the least common multiple (LCM) for addition and subtraction.
- Check for Restricted Values: Determine any values of the variable that would make the denominator zero and exclude these from the solution. These are the restrictions on the rational expression.
For example, consider the rational expression:
\[\dfrac{2x^2 + 26x + 84}{2x^2 + 12x - 14}\]
- Factor both the numerator and the denominator:
- Numerator: \(2(x^2 + 13x + 42) = 2(x + 6)(x + 7)\)
- Denominator: \(2(x^2 + 6x - 7) = 2(x + 7)(x - 1)\)
- Cancel out the common factor of \(2(x + 7)\):
- \[\dfrac{2(x + 6)(x + 7)}{2(x + 7)(x - 1)} = \dfrac{x + 6}{x - 1}\]
- State the restrictions: \(x \neq -7, 1\).
By following these steps, you can simplify any rational expression effectively.
Steps for Simplifying Rational Expressions
Simplifying rational expressions involves reducing the expression to its simplest form. Here are the steps to simplify rational expressions effectively:
- Factor Both Numerator and Denominator: Start by factoring both the numerator and the denominator of the rational expression completely. Look for common factors, differences of squares, and other factoring techniques.
- Identify and Cancel Common Factors: Once both parts are factored, identify any common factors between the numerator and the denominator. These common factors can be canceled out, as long as they are not zero.
- Simplify the Expression: After canceling the common factors, simplify what remains in the numerator and the denominator to get the simplified form of the rational expression.
- Check for Domain Restrictions: Determine any values that make the original denominator zero and exclude these from the domain of the expression. These values are called restrictions and are important to state alongside the simplified expression.
Let's look at an example to illustrate these steps:
Example: Simplify \(\frac{x^2 - 9}{x^2 - 3x}\).
- Factor the numerator and the denominator:
- Numerator: \(x^2 - 9 = (x + 3)(x - 3)\)
- Denominator: \(x^2 - 3x = x(x - 3)\)
- Identify and cancel the common factors:
- The common factor is \(x - 3\).
- Cancel \(x - 3\) in both numerator and denominator.
- Simplify the expression:
- After canceling, we are left with \(\frac{x + 3}{x}\).
- Check for domain restrictions:
- From the original expression, \(x^2 - 3x\) must not be zero, so \(x \neq 0\) and \(x \neq 3\).
Therefore, the simplified form of \(\frac{x^2 - 9}{x^2 - 3x}\) is \(\frac{x + 3}{x}\) with the restrictions \(x \neq 0\) and \(x \neq 3\).

Operations on Rational Expressions
Understanding how to perform operations on rational expressions is crucial for simplifying these expressions. There are four primary operations that can be performed: addition, subtraction, multiplication, and division. Each operation has specific steps to follow for simplifying rational expressions effectively.
Addition
To add two rational expressions, follow these steps:
- Write all terms separately as a sum.
- Find the least common multiple (LCM) of the denominators to make them common.
- Add the numerators over the common denominator.
- Simplify by canceling like terms.
Subtraction
Subtracting rational expressions is similar to addition:
- Write all terms separately as a difference.
- Find the LCM of the denominators.
- Subtract the numerators over the common denominator.
- Simplify by canceling like terms.
Multiplication
For multiplying rational expressions, follow these steps:
- Multiply the numerators together and the denominators together.
- Apply the distributive property to expand any polynomials.
- Simplify the resulting expression by combining like terms.
- Rewrite the expression in its simplest form.
Division
Dividing rational expressions involves a few additional steps:
- Write the expression with the division sign.
- Take the reciprocal of the divisor and change the division sign to multiplication.
- Multiply the numerators and denominators accordingly.
- Simplify by canceling like terms.
- Reduce the expression to its simplest form.
Adding Rational Expressions
Adding rational expressions involves combining fractions with different denominators. Here are the steps to add rational expressions:
-
Find a common denominator:
The first step is to find the least common denominator (LCD) of the rational expressions. This is similar to finding the common denominator for numeric fractions.
- Factor each denominator completely.
- Identify the highest powers of each unique factor in the denominators.
- Multiply these factors together to get the LCD.
-
Rewrite each rational expression:
Convert each rational expression so that they all have the same common denominator.
- Divide the LCD by the denominator of each fraction.
- Multiply the numerator and the denominator of each fraction by this quotient.
-
Add the numerators:
Once all the rational expressions have the same denominator, add the numerators together and keep the common denominator.
- Combine like terms if possible.
-
Simplify the resulting expression:
Simplify the resulting rational expression by factoring the numerator and the denominator and canceling any common factors.
Here is an example to illustrate the process:
| \(\frac{3}{x+2} + \frac{2}{x-3}\) |
|
By following these steps, you can add any rational expressions effectively.
Subtracting Rational Expressions
Subtracting rational expressions follows a similar process to adding them, but with a slight difference in the operation performed.
To subtract rational expressions, follow these steps:
- Determine a common denominator for the rational expressions involved.
- Subtract the numerators of the rational expressions.
- Simplify the resulting rational expression, if possible, by factoring and canceling out common factors.
Here's an example to illustrate:
| \(\frac{3}{x} - \frac{2}{x}\) | Given rational expressions to subtract. |
| \(\frac{3 - 2}{x}\) | Combine the numerators over the common denominator \(x\). |
| \(\frac{1}{x}\) | Resulting simplified rational expression after subtraction. |
Always ensure to simplify the final expression to its lowest terms whenever possible.
Multiplying Rational Expressions
Multiplying rational expressions is similar to multiplying fractions. Follow these steps to multiply rational expressions effectively:
- Factor both the numerators and the denominators of the rational expressions.
- Multiply the numerators together to get a single numerator.
- Multiply the denominators together to get a single denominator.
- Simplify the resulting expression by canceling out common factors in the numerator and the denominator.
Let's go through an example to illustrate these steps:
Example: Multiply the rational expressions \( \frac{x^2 - 9}{x^2 - 4x + 4} \) and \( \frac{x + 2}{x^2 + x - 6} \)
- Factor the numerators and denominators:
- Multiply the numerators together:
- Multiply the denominators together:
- Simplify the expression:
\( \frac{(x - 3)(x + 3)}{(x - 2)^2} \cdot \frac{(x + 2)}{(x - 2)(x + 3)} \)
Numerator: \( (x - 3)(x + 3)(x + 2) \)
Denominator: \( (x - 2)^2(x - 2)(x + 3) \)
Simplify by canceling out common factors:
\( \frac{(x - 3)(x + 2)}{(x - 2)^3} \)
The simplified form of the multiplied rational expressions is \( \frac{(x - 3)(x + 2)}{(x - 2)^3} \).
By following these steps, you can multiply any rational expressions and simplify them efficiently.
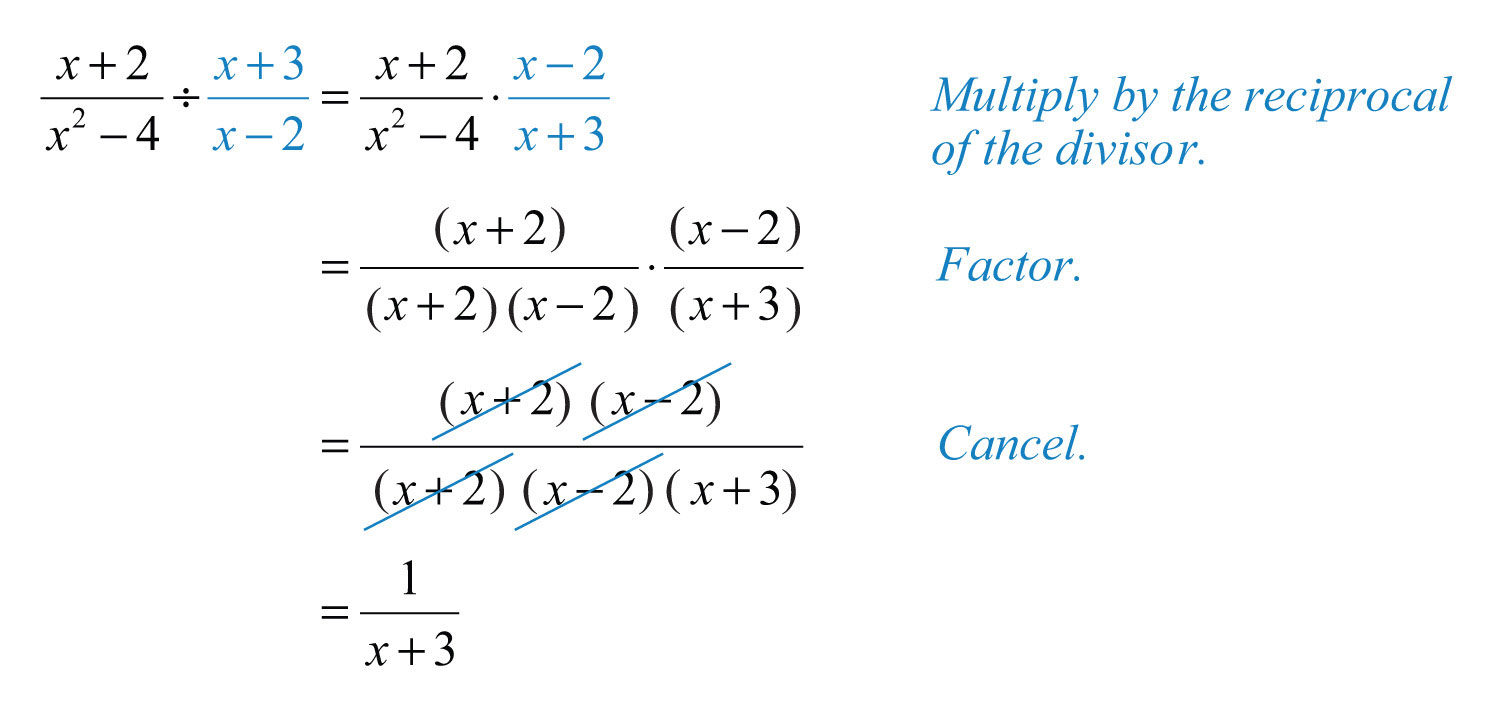
Dividing Rational Expressions
Dividing rational expressions involves a few straightforward steps. Here is a detailed guide on how to divide rational expressions effectively:
-
Write the Division as Multiplication: To divide rational expressions, you multiply by the reciprocal of the divisor. For example, to divide \( \frac{A(x)}{B(x)} \) by \( \frac{C(x)}{D(x)} \), rewrite it as:
\[ \frac{A(x)}{B(x)} \div \frac{C(x)}{D(x)} = \frac{A(x)}{B(x)} \times \frac{D(x)}{C(x)} \] -
Factor Both Numerator and Denominator: Factorize the numerators and denominators to their simplest forms. This makes it easier to identify common factors that can be canceled out. For instance:
\[ \frac{A(x)}{B(x)} \times \frac{D(x)}{C(x)} = \frac{(factorized\; A(x))}{(factorized\; B(x))} \times \frac{(factorized\; D(x))}{(factorized\; C(x))} \] -
Cancel Common Factors: Identify and cancel any common factors between the numerators and the denominators. This step simplifies the expression further. For example:
\[ \frac{(A(x)\; factors)}{(B(x)\; factors)} \times \frac{(D(x)\; factors)}{(C(x)\; factors)} \] Cancel common factors to get: \[ \frac{remaining\; factors}{remaining\; factors} \] -
Simplify the Result: Once all common factors are canceled, simplify the remaining expression. The result will be the quotient of the original division problem.
Here is an example to illustrate the process:
Example: Divide \( \frac{2x^2 - 8}{3x^2} \) by \( \frac{4x}{9} \).
-
Rewrite the division as multiplication:
\[ \frac{2x^2 - 8}{3x^2} \div \frac{4x}{9} = \frac{2x^2 - 8}{3x^2} \times \frac{9}{4x} \] -
Factorize the numerators and denominators:
\[ \frac{2(x^2 - 4)}{3x^2} \times \frac{9}{4x} = \frac{2(x - 2)(x + 2)}{3x^2} \times \frac{9}{4x} \] -
Cancel common factors:
\[ \frac{2(x - 2)(x + 2)}{3x^2} \times \frac{9}{4x} = \frac{2(x - 2)(x + 2) \cdot 9}{3x^2 \cdot 4x} \] Simplifying, we get: \[ \frac{2 \cdot 9 (x - 2)(x + 2)}{3 \cdot 4x^3} = \frac{18 (x - 2)(x + 2)}{12x^3} \] -
Simplify the result:
\[ \frac{18 (x - 2)(x + 2)}{12x^3} = \frac{3 (x - 2)(x + 2)}{2x^3} \]
The final simplified form is \( \frac{3 (x - 2)(x + 2)}{2x^3} \).
Examples and Solutions
Here, we will walk through some examples of simplifying rational expressions step by step. These examples will help you understand the process and see how to apply the steps in different scenarios.
Example 1: Simplifying a Rational Expression
Simplify the following rational expression:
\[ \frac{6x^2 + 9x}{3x} \]
- First, factor out the greatest common factor (GCF) in the numerator.
- Next, cancel the common factor in the numerator and the denominator.
\[ \frac{3x(2x + 3)}{3x} \]
\[ \frac{\cancel{3x}(2x + 3)}{\cancel{3x}} = 2x + 3 \]
The simplified form is \( 2x + 3 \).
Example 2: Simplifying a More Complex Rational Expression
Simplify the following rational expression:
\[ \frac{x^2 - 4}{x^2 - x - 6} \]
- Factor the numerator and the denominator.
- Rewrite the expression with the factored forms.
- Cancel the common factors in the numerator and the denominator.
Numerator: \[ x^2 - 4 = (x - 2)(x + 2) \]
Denominator: \[ x^2 - x - 6 = (x - 3)(x + 2) \]
\[ \frac{(x - 2)(x + 2)}{(x - 3)(x + 2)} \]
\[ \frac{(x - 2)\cancel{(x + 2)}}{(x - 3)\cancel{(x + 2)}} = \frac{x - 2}{x - 3} \]
The simplified form is \(\frac{x - 2}{x - 3}\).
Example 3: Simplifying a Rational Expression with Polynomial Terms
Simplify the following rational expression:
\[ \frac{2x^3 - 8x}{4x^2} \]
- Factor out the greatest common factor (GCF) in the numerator.
- Factor the remaining quadratic term in the numerator.
- Cancel the common factors in the numerator and the denominator.
\[ \frac{2x(x^2 - 4)}{4x^2} \]
\[ x^2 - 4 = (x - 2)(x + 2) \]
So, the expression becomes: \[ \frac{2x(x - 2)(x + 2)}{4x^2} \]
\[ \frac{\cancel{2x}(x - 2)(x + 2)}{2\cancel{2x}x} = \frac{(x - 2)(x + 2)}{2x} \]
The simplified form is \(\frac{(x - 2)(x + 2)}{2x}\).
These examples demonstrate how to simplify rational expressions by factoring and canceling common terms. Practice with various expressions to become more comfortable with these steps.
Using Online Calculators
Online calculators for simplifying rational expressions are powerful tools that can assist you in learning and solving complex algebraic problems with ease. Here is a step-by-step guide on how to use these calculators effectively:
- Choose the Calculator Type:
First, select the type of operation you want to perform. Most online calculators offer options like simplifying, adding, subtracting, multiplying, and dividing rational expressions.
- Input the Expression:
Enter the rational expression you want to simplify. For example, if you want to simplify \( \frac{2x^2 + 4x}{x^2 - 4} \), type it into the appropriate input fields.
- Select the Operation:
If the calculator has multiple functionalities, select the specific operation (e.g., simplify, multiply, divide) you want to perform.
- Perform the Calculation:
Click the 'Calculate' button to execute the operation. The calculator will process your input and provide a step-by-step solution.
- Review the Steps:
Most advanced calculators will show the steps involved in the simplification process. This feature is particularly useful for learning and understanding how the simplification is done.
Example
Let's simplify the rational expression \( \frac{2x^2 + 4x}{x^2 - 4} \) using an online calculator:
- Input the expression \( \frac{2x^2 + 4x}{x^2 - 4} \).
- Select the 'Simplify' option.
- Click 'Calculate'.
- Review the steps provided by the calculator:
The calculator may show the following steps:
- Factor the numerator: \( 2x(x + 2) \)
- Factor the denominator: \( (x - 2)(x + 2) \)
- Cancel out the common factors: \( \frac{2x(x + 2)}{(x - 2)(x + 2)} \rightarrow \frac{2x}{x - 2} \)
The simplified form is \( \frac{2x}{x - 2} \).
Benefits of Using Online Calculators
- Accuracy: Ensures precise calculations.
- Learning Tool: Provides step-by-step solutions to help you understand the process.
- Time-Saving: Quickly simplifies complex expressions.
- Accessibility: Available online anytime and often free of charge.
Using these tools can greatly enhance your understanding and efficiency in handling rational expressions.
Common Mistakes and Tips
When simplifying rational expressions, students often make some common mistakes. Here are a few to watch out for and some tips to avoid them:
- Not Factoring Completely: Ensure that both the numerator and the denominator are factored completely before attempting to simplify.
- Incorrectly Cancelling Terms: Only terms that are common factors of both the numerator and the denominator can be cancelled. For example, in the expression \(\dfrac{6x}{2x}\), the \(x\) terms can be cancelled, resulting in \(\dfrac{6}{2} = 3\).
- Ignoring Restrictions on the Variable: Always identify and state the values for which the expression is undefined, typically where the denominator equals zero.
- Misapplying Operations: Be careful when performing operations such as addition, subtraction, multiplication, and division. Ensure that you follow the correct procedures for each operation.
Tips for Simplifying Rational Expressions
Here are some tips to help simplify rational expressions correctly:
- Factor First: Always start by factoring the numerator and the denominator completely. For example:
Given the expression \(\dfrac{2x^2 + 26x + 84}{2x^2 + 12x - 14}\), factor both parts:
\[
\dfrac{2(x^2 + 13x + 42)}{2(x^2 + 6x - 7)} = \dfrac{2(x + 6)(x + 7)}{2(x + 7)(x - 1)}
\] - Cancel Common Factors: Once factored, cancel out any common factors in the numerator and denominator. In the previous example, cancel the common factor \((x + 7)\):
\[
\dfrac{2(x + 6)(x + 7)}{2(x + 7)(x - 1)} = \dfrac{x + 6}{x - 1}
\] - State Restrictions: Identify and state the values that make the denominator zero. In the example, \(x \neq -7\) and \(x \neq 1\).
- Check Your Work: Always substitute a few values back into the original and simplified expressions to verify that they are equivalent.

Practice Problems
Practice is essential to mastering the simplification of rational expressions. Below are a variety of problems to help you hone your skills. Follow each step carefully and verify your answers.
-
Problem 1: Simplify the rational expression
\[ \frac{6x^2 - 18x}{3x} \]
- Factor the numerator: \[ 6x^2 - 18x = 6x(x - 3) \]
- Write the expression as: \[ \frac{6x(x - 3)}{3x} \]
- Cancel the common factor \( 3x \): \[ \frac{6(x - 3)}{3} = 2(x - 3) \]
- Simplified form: \[ 2(x - 3) \]
-
Problem 2: Simplify the rational expression
\[ \frac{x^2 - 9}{x^2 + 6x + 9} \]
- Factor the numerator: \[ x^2 - 9 = (x - 3)(x + 3) \]
- Factor the denominator: \[ x^2 + 6x + 9 = (x + 3)^2 \]
- Write the expression as: \[ \frac{(x - 3)(x + 3)}{(x + 3)(x + 3)} \]
- Cancel the common factor \( x + 3 \): \[ \frac{x - 3}{x + 3} \]
- Simplified form: \[ \frac{x - 3}{x + 3} \]
-
Problem 3: Simplify the rational expression
\[ \frac{x^2 - 4x + 4}{x^2 - x - 6} \]
- Factor the numerator: \[ x^2 - 4x + 4 = (x - 2)^2 \]
- Factor the denominator: \[ x^2 - x - 6 = (x - 3)(x + 2) \]
- Write the expression as: \[ \frac{(x - 2)^2}{(x - 3)(x + 2)} \]
- No common factors to cancel.
- Simplified form: \[ \frac{(x - 2)^2}{(x - 3)(x + 2)} \]
-
Problem 4: Simplify the rational expression
\[ \frac{2x^3 - 8x}{4x^2 - 16} \]
- Factor the numerator: \[ 2x^3 - 8x = 2x(x^2 - 4) = 2x(x - 2)(x + 2) \]
- Factor the denominator: \[ 4x^2 - 16 = 4(x^2 - 4) = 4(x - 2)(x + 2) \]
- Write the expression as: \[ \frac{2x(x - 2)(x + 2)}{4(x - 2)(x + 2)} \]
- Cancel the common factors \( 2(x - 2)(x + 2) \): \[ \frac{x}{2} \]
- Simplified form: \[ \frac{x}{2} \]
These practice problems will help reinforce your understanding of simplifying rational expressions. Try solving similar problems to gain confidence and proficiency.
Additional Resources
To further enhance your understanding and proficiency in simplifying rational expressions, here are some additional resources that you can explore:
- Online Calculators: Utilize online rational expression calculators for step-by-step solutions. These tools are especially helpful for verifying your manual calculations and providing detailed explanations.
- Tutorial Videos: There are numerous educational platforms like Khan Academy, YouTube, and Coursera that offer tutorial videos on rational expressions. Visual aids can significantly improve your comprehension.
- Practice Worksheets: Websites like Math-Aids.com and Kuta Software provide printable worksheets with a variety of problems for practice. Consistent practice helps in mastering the techniques.
- Interactive Learning Platforms: Platforms such as IXL and Brilliant offer interactive exercises that adapt to your learning pace, providing instant feedback and detailed solutions.
- Mathematics Textbooks: Books such as "Algebra for College Students" by Blitzer or "Intermediate Algebra" by Bittinger offer comprehensive coverage of rational expressions along with practice problems and solutions.
- Online Forums: Participate in online forums like Stack Exchange, Reddit, or Math Help Boards where you can ask questions, share insights, and get assistance from a community of learners and experts.
- Educational Websites: Websites like Purplemath, Mathway, and Paul's Online Math Notes provide in-depth explanations, examples, and practice problems for various algebraic topics including rational expressions.
By leveraging these resources, you can gain a deeper understanding and become proficient in simplifying rational expressions. Happy learning!
FAQs
Here are some frequently asked questions about simplifying rational expressions:
- What is a rational expression?
- How do you simplify a rational expression?
- What is the difference between a proper and an improper rational expression?
- Can rational expressions have variables in the denominator?
- How do you add or subtract rational expressions?
- How do you multiply or divide rational expressions?
- Why is it important to simplify rational expressions?
A rational expression is a fraction where the numerator and the denominator are both polynomials. The denominator cannot be zero.
To simplify a rational expression, factor both the numerator and the denominator, then cancel out any common factors. For example:
Given: \(\frac{x^2 - 4}{x^2 - x - 6}\)
Factor the numerator and the denominator:
\(\frac{(x + 2)(x - 2)}{(x - 3)(x + 2)}\)
Cancel the common factor \((x + 2)\):
\(\frac{x - 2}{x - 3}\)
A proper rational expression has a numerator of a lower degree than the denominator, while an improper rational expression has a numerator of equal or higher degree than the denominator.
Yes, rational expressions typically have variables in the denominator. However, these variables cannot make the denominator equal to zero.
To add or subtract rational expressions, first find a common denominator. Then, combine the numerators over this common denominator and simplify. For example:
Given: \(\frac{1}{x} + \frac{1}{x+1}\)
Common denominator: \(x(x+1)\)
Combine: \(\frac{x+1 + x}{x(x+1)} = \frac{2x+1}{x(x+1)}\)
To multiply rational expressions, multiply the numerators together and the denominators together, then simplify. To divide, multiply by the reciprocal of the divisor. For example:
Multiplication: \(\frac{x}{y} \times \frac{a}{b} = \frac{xa}{yb}\)
Division: \(\frac{x}{y} \div \frac{a}{b} = \frac{x}{y} \times \frac{b}{a} = \frac{xb}{ya}\)
Simplifying rational expressions makes them easier to work with and understand. It can also reveal properties and solutions that are not immediately obvious.
Học cách vẽ đồ thị hàm số hữu tỉ qua 6 bước đơn giản và dễ hiểu.
Cách Vẽ Đồ Thị Hàm Số Hữu Tỉ Bằng 6 Bước
READ MORE:
Hướng dẫn mở rộng đa thức bằng máy tính để thu hút người xem và đảm bảo chính tả.
Cách mở rộng đa thức bằng máy tính