Understanding the Square Root of 15 in Simplified Radical Form

The square root of 15 cannot be simplified further in its radical form. This is because 15 is not a perfect square and does not have any perfect square factors other than 1. Below are the steps to express the square root of 15 in its simplest radical form.

Step-by-Step Process

1. Identify the prime factors of 15:
   • 15 = 3 × 5
2. Write the square root of 15 in terms of its prime factors:
3. Since neither 3 nor 5 is a perfect square, the expression \(\sqrt{15}\) cannot be simplified further.

Decimal Form

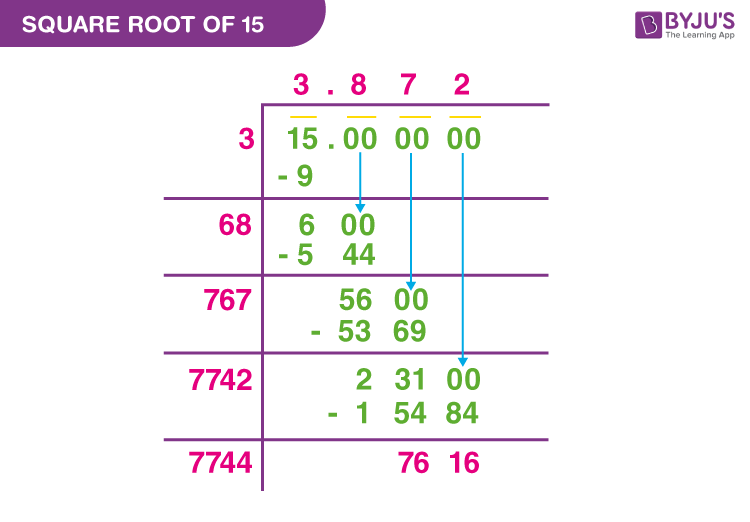
The decimal approximation of the square root of 15 is approximately 3.87298, which can be rounded to 3.873 for practical purposes.

Examples

Example 1: Length of a Side of a Square

If the area of a square is 15 square units, the length of each side can be found using the square root of 15:

\(\text{Side length} = \sqrt{15} \approx 3.873 \, \text{units}\)

Example 2: Prime Factorization

Using prime factorization, we express 15 as the product of its prime factors:

\(15 = 3 \times 5\)

Thus, \(\sqrt{15} = \sqrt{3 \times 5}\) and it remains in this form as it cannot be simplified further.

Key Points

• The square root of 15 is an irrational number.
• Its simplest radical form is \(\sqrt{15}\).
• In decimal form, it is approximately 3.87298.

Understanding these steps and examples helps in grasping why \(\sqrt{15}\) cannot be simplified beyond its current form.

The square root of a number is a value that, when multiplied by itself, gives the original number. In the case of 15, the square root is denoted as √15. Simplifying square roots involves expressing the root in its simplest radical form, which can make further mathematical operations more straightforward. The square root of 15 is an irrational number, meaning it cannot be exactly expressed as a simple fraction. This guide will walk you through the process of simplifying √15, providing an understanding of the principles behind it, and illustrating its applications.

In mathematics, radicals are used to denote roots, and the simplest radical form is achieved by factoring the number under the root into its prime factors. For 15, the prime factors are 3 and 5. Unlike some other numbers, the square root of 15 cannot be simplified further because there are no perfect square factors other than 1. Therefore, √15 remains in its simplest form as √15.

This tutorial will cover various aspects of simplifying radicals, including a step-by-step approach to understanding and breaking down the number 15, identifying its prime factors, and ensuring that you avoid common mistakes. We will also provide examples and practice problems to solidify your understanding and show the practical applications of simplified radicals in mathematical problems.

The square root of a number is a value that, when multiplied by itself, gives the original number. In mathematical notation, the square root of a number n is written as √n. For example, the square root of 9 is 3 because 3 × 3 = 9.

Square roots can be classified into two categories: perfect squares and non-perfect squares. A perfect square is a number that has an integer as its square root. Examples include 1, 4, 9, 16, and so on. Non-perfect squares are numbers that do not have an integer as their square root, such as 2, 3, 5, and 15.

When dealing with square roots, it is essential to understand that the square root function has two values: a positive and a negative root. This is because both positive and negative numbers, when squared, yield a positive result. For instance, both 3 and -3 are square roots of 9 because 3 × 3 = 9 and -3 × -3 = 9.

Square roots are also related to exponents. Specifically, the square root of a number is the same as raising that number to the power of one-half. In other words:

$$\sqrt{n} = n^{1/2}$$

Another important concept is the principal square root, which is the non-negative square root of a number. When we refer to the square root of a number without any additional context, we typically mean the principal square root.

Here are some key points to remember about square roots:

• The square root of a number n is written as √n.
• Every positive number has two square roots: one positive and one negative.
• The principal square root is the non-negative square root.
• Square roots are the inverse operation of squaring a number.
• The square root of a number can be expressed as an exponent: √n = n^{1/2}.

Understanding these fundamentals is crucial when working with square roots and will help you in simplifying expressions involving square roots, such as √15.

The simplified radical form of a square root is a way of expressing the square root such that the radicand (the number under the square root sign) has no perfect square factors other than 1. In other words, it is the most reduced form of the radical expression.

To understand this, let’s go through the general steps to simplify a square root:

1. Prime Factorization: Break down the number inside the square root into its prime factors. For example, the number 15 can be factored into 3 and 5.
2. Pairing Factors: Identify pairs of the same prime factors. If a factor appears twice, it can be taken out of the square root. However, for the number 15 (which is \( \sqrt{15} \)), since there are no pairs of the same factors (3 and 5 are different primes), it remains as \( \sqrt{15} \).
3. Writing the Simplified Form: If there are any pairs, they are moved outside the square root. Since 15 has no pairs of prime factors, \( \sqrt{15} \) is already in its simplest form.

To illustrate, consider another example:

• Simplify \( \sqrt{12} \):
  • Prime factorization of 12: \( 2^2 \times 3 \)
  • Pairs: \( 2^2 \) (since \( 2 \times 2 = 4 \), a perfect square)
  • Simplified form: \( \sqrt{12} = \sqrt{2^2 \times 3} = 2\sqrt{3} \)

Therefore, the simplified radical form ensures that the expression under the square root has no perfect square factors, making it more manageable for calculations and understanding.

Simplifying the square root of 15 involves determining if it can be broken down into simpler components. Let's go through this step-by-step:

1. List the Factors: Identify all factors of 15.

   • Factors of 15: 1, 3, 5, 15

2. Identify Perfect Squares: Check if any of these factors are perfect squares. A perfect square is a number that has an integer as its square root (e.g., 1, 4, 9, 16).

   • The only perfect square factor of 15 is 1, but since it's just 1, it doesn't help in simplifying the square root further.

3. Separate the Radicals: If there were perfect square factors, we would express √15 as the product of two square roots, but since there are none other than 1, we leave it as it is.

   The prime factorization of 15 is 3 and 5, neither of which are perfect squares. Therefore:

   \[\sqrt{15}\] remains as it is.

Since 15 cannot be simplified further in terms of perfect square factors, the simplest radical form of √15 is \[\sqrt{15}\]. This indicates that the square root of 15 is already in its simplest form.

To summarize:

• Factors of 15: 1, 3, 5, 15
• No perfect square factors other than 1
• Therefore, \[\sqrt{15}\] cannot be simplified further.

We have confirmed that \[\sqrt{15}\] is in its simplest radical form.

To simplify the square root of 15, it's important to understand the number itself and its factors. Here is a detailed breakdown of the number 15:

• Factors of 15: The factors of 15 are the numbers that can be multiplied together to get 15. These factors are 1, 3, 5, and 15.
• Prime Factorization: Prime factorization involves expressing 15 as a product of its prime numbers. The prime factorization of 15 is 3 and 5. This can be written as:

  \[
  15 = 3 \times 5
  \]

• Perfect Squares: Perfect squares are numbers that have integers as their square roots. The only perfect square factor of 15 is 1, which means the square root of 15 cannot be simplified further because it does not have any perfect square factors other than 1.

Since 15 is already expressed in its simplest form with prime factorization, we can use this understanding to further simplify or analyze expressions involving the square root of 15. For example, knowing the prime factors can help in further calculations or understanding the properties of the number.

The prime factorization of a number is the process of expressing the number as a product of its prime factors. To find the prime factorization of 15, we need to identify the prime numbers that multiply together to give the original number.

1. First, we start with the number 15.
2. We find the smallest prime number that divides 15, which is 3. So, we divide 15 by 3:

15 ÷ 3 = 5

3. Next, we consider the quotient, which is 5. Since 5 is also a prime number, we stop the process here.
4. Therefore, the prime factors of 15 are 3 and 5.

We can express 15 as the product of its prime factors:

15 = 3 × 5

When considering the square root of 15, we use the property of square roots that allows us to take the square root of each prime factor separately:

√15 = √(3 × 5)

Since neither 3 nor 5 is a perfect square, we cannot simplify this further. Therefore, the square root of 15 remains in its simplest radical form:

√15

The square root of 15 is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal form is non-repeating and non-terminating. To simplify the square root of 15 in its radical form, follow these steps:

1. Prime Factorization:

   Begin by expressing 15 as a product of its prime factors. The prime factorization of 15 is:

   \(15 = 3 \times 5\)

2. Check for Perfect Squares:

   Next, identify any pairs of prime factors that can be simplified. In this case, neither 3 nor 5 are perfect squares, and there are no pairs of prime factors that can be combined to form a perfect square. Therefore, the square root of 15 cannot be simplified further in radical form.

   The simplified radical form remains:

   \(\sqrt{15}\)

3. Understanding the Result:

   Since there are no perfect square factors in 15 other than 1, the square root of 15 remains as \(\sqrt{15}\) in its simplest radical form.

   In decimal form, the square root of 15 is approximately:

   \(\sqrt{15} \approx 3.87298\)

Thus, \(\sqrt{15}\) is already in its simplest radical form and cannot be simplified further.

When simplifying the square root of 15, students often make common mistakes that can lead to incorrect results. Being aware of these mistakes helps ensure accuracy:

1. Incorrect Prime Factorization:

   Failing to correctly factorize 15 as \(3 \times 5\). This mistake prevents proper simplification since the process starts with identifying the prime factors.

2. Assuming Simplification is Possible:

   Attempting to simplify \(\sqrt{15}\) further when it is already in its simplest form. Recognize that not all square roots can be simplified if they don't have perfect square factors.

3. Confusing Multiplication and Addition:

   Misapplying rules by treating the sum of square roots as a single square root, such as mistakenly believing \(\sqrt{15}\) can be simplified like \(\sqrt{9 + 6}\).

4. Improper Use of Radical Rules:

   Misusing properties of radicals, such as incorrectly applying the product rule for square roots. For example, mistakenly simplifying \(\sqrt{15} \times \sqrt{15}\) as \(\sqrt{225}\) instead of recognizing it equals 15.

5. Not Simplifying Intermediate Steps:

   Overlooking the simplification of intermediate steps, leading to more complex calculations. Always simplify expressions at each step to avoid compounded errors.

By being mindful of these common errors, you can improve your understanding and accuracy in simplifying radicals like \(\sqrt{15}\).

Here are some examples and practice problems to help you understand how to simplify radical expressions, including the square root of 15. Let's look at the detailed step-by-step solutions:

Example 1: Simplifying \(\sqrt{15}\)

The number 15 does not have any perfect square factors other than 1, so it cannot be simplified further. Thus, the simplified form of \(\sqrt{15}\) is:

\(\sqrt{15}\)

Example 2: Simplifying \(\sqrt{72}\)

First, find the largest perfect square factor of 72:

• 72 can be factored into 36 and 2 (since 36 is a perfect square).

Now, apply the property of square roots:

\(\sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2}\)

Example 3: Simplifying \(\sqrt{48}\)

Find the largest perfect square factor of 48:

• 48 can be factored into 16 and 3 (since 16 is a perfect square).

Now, apply the property of square roots:

\(\sqrt{48} = \sqrt{16 \times 3} = \sqrt{16} \times \sqrt{3} = 4\sqrt{3}\)

Example 4: Simplifying \(\sqrt{200}\)

Find the largest perfect square factor of 200:

• 200 can be factored into 100 and 2 (since 100 is a perfect square).

Now, apply the property of square roots:

\(\sqrt{200} = \sqrt{100 \times 2} = \sqrt{100} \times \sqrt{2} = 10\sqrt{2}\)

Practice Problems

Try simplifying the following radicals. Remember to find the largest perfect square factor and apply the properties of square roots:

1. Simplify \(\sqrt{50}\)
2. Simplify \(\sqrt{75}\)
3. Simplify \(\sqrt{98}\)
4. Simplify \(\sqrt{32}\)
5. Simplify \(\sqrt{18}\)

Solutions:

1. \(\sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2}\)
2. \(\sqrt{75} = \sqrt{25 \times 3} = \sqrt{25} \times \sqrt{3} = 5\sqrt{3}\)
3. \(\sqrt{98} = \sqrt{49 \times 2} = \sqrt{49} \times \sqrt{2} = 7\sqrt{2}\)
4. \(\sqrt{32} = \sqrt{16 \times 2} = \sqrt{16} \times \sqrt{2} = 4\sqrt{2}\)
5. \(\sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} = 3\sqrt{2}\)

Simplified radicals, including those like √15, find numerous applications across various fields. Understanding how to simplify and manipulate these expressions is essential for both theoretical and practical purposes. Below are some common applications:

• Geometry and Trigonometry:

  Simplified radicals are often used to express lengths, areas, and angles in geometric figures. For example, the diagonal of a square with side length 1 is expressed as √2, which is a simplified radical. Similarly, in trigonometry, the exact values of sine, cosine, and tangent for special angles are often given in simplified radical form.

• Physics:

  In physics, simplified radicals appear in formulas involving wave equations, quantum mechanics, and relativity. For instance, the wavelength of a particle in quantum mechanics might be expressed in terms of simplified radicals.

• Engineering:

  Engineering problems frequently involve calculations with square roots and other radicals. For example, when determining the stress on a material or the frequency of an oscillating system, simplified radicals are used to simplify the results.

• Computer Graphics:

  In computer graphics, calculations involving distances and transformations often use simplified radicals. For instance, the distance formula between two points in a plane, √((x2 - x1)² + (y2 - y1)²), frequently requires simplification to make computations more efficient.

• Architecture:

  Architects use simplified radicals in design and structural analysis to calculate dimensions and areas. This helps in creating accurate and efficient designs.

• Finance:

  In finance, simplified radicals can appear in models involving risk assessments and optimization problems, particularly in the context of the geometric mean and other statistical measures.

Understanding how to work with simplified radicals not only simplifies complex mathematical expressions but also enhances problem-solving skills in various scientific and engineering disciplines.

The square root of 15, expressed in its simplest radical form as \( \sqrt{15} \), illustrates the intriguing nature of irrational numbers. While it cannot be simplified further, its value remains significant in both theoretical and practical applications. The process of finding the square root of 15 involves understanding its prime factors and acknowledging its place among non-perfect squares.

Through the prime factorization method, we see that \( \sqrt{15} \) is composed of the product of the square roots of its prime factors: \( \sqrt{3} \) and \( \sqrt{5} \). This reinforces the concept that not all numbers can be neatly expressed as integers or simple fractions, highlighting the importance of radicals in mathematics.

From geometry to algebra, the presence of irrational numbers like \( \sqrt{15} \) is crucial. Whether solving quadratic equations, analyzing patterns, or exploring higher-level mathematics, the understanding of these radicals enriches our comprehension of the mathematical world.

In conclusion, while \( \sqrt{15} \) cannot be simplified beyond its radical form, its study offers valuable insights into the nature of numbers and their properties. Embracing the complexity and beauty of such numbers is essential for anyone delving into the realm of mathematics.