Topic is 6 a perfect square: Have you ever wondered if 6 is a perfect square? In this article, we delve into the mathematical concepts behind perfect squares and explore why 6 doesn't fit the criteria. Join us as we uncover the fascinating properties of perfect squares and clarify common misconceptions. Let's explore the truth together!
Table of Content
- Is 6 a Perfect Square?
- Introduction to Perfect Squares
- Mathematical Explanation
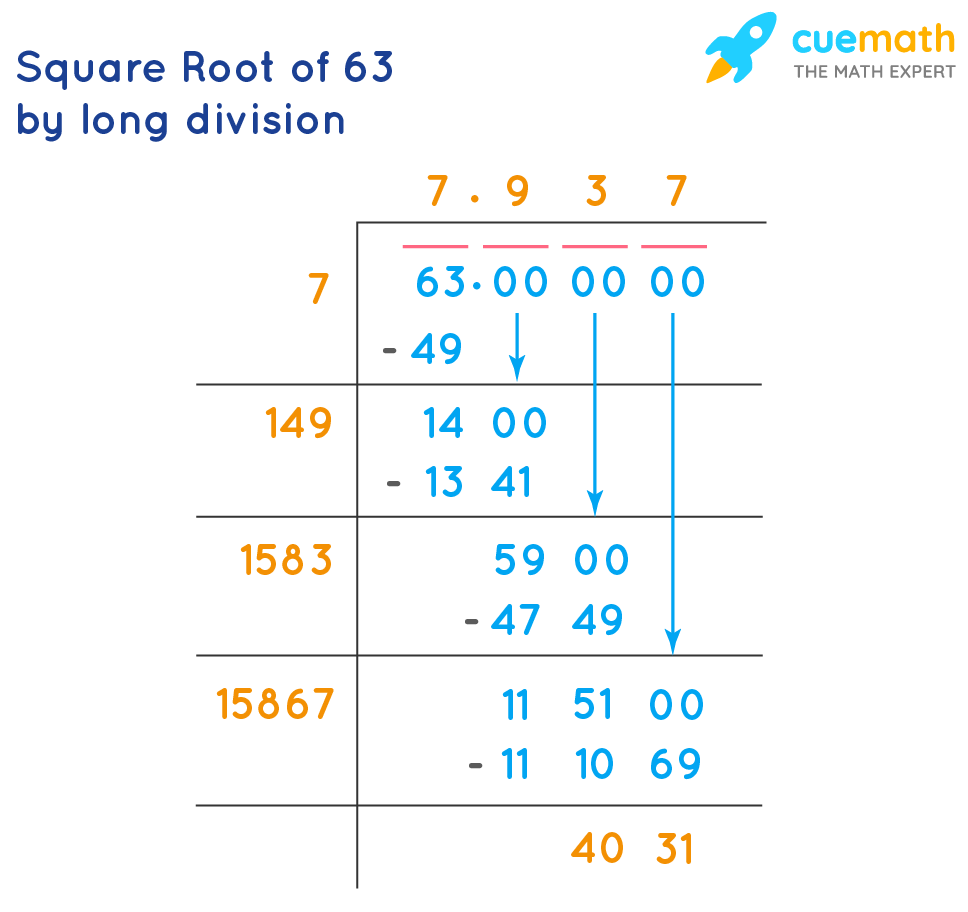
- Calculating the Square Root of 6
- Properties of Perfect Squares
- Examples of Perfect Squares
- Why 6 is Not a Perfect Square
- Misconceptions About Perfect Squares
- Real-World Applications
- YOUTUBE: Khám phá căn bậc hai của các số chính phương cùng Thầy J. Video này giúp bạn hiểu rõ hơn về khái niệm số chính phương và cách tính căn bậc hai.
Is 6 a Perfect Square?
To determine if a number is a perfect square, we need to check if it can be expressed as the product of an integer with itself.
Definition of a Perfect Square
A perfect square is a number that can be written as \( n^2 \), where \( n \) is an integer. In mathematical terms:
\[ n^2 = k \]
where \( k \) is the perfect square and \( n \) is an integer.
Evaluation of 6
Let's check if 6 can be expressed as \( n^2 \):
\[ n^2 = 6 \]
Taking the square root of both sides, we get:
\[ n = \sqrt{6} \]
The square root of 6 is approximately 2.449, which is not an integer. Therefore:
\[ \sqrt{6} \notin \mathbb{Z} \]
Since the square root of 6 is not an integer, 6 cannot be written as the product of an integer with itself.
Conclusion
Based on the above evaluation, we can conclude that 6 is not a perfect square.
READ MORE:
Introduction to Perfect Squares
A perfect square is a number that can be expressed as the product of an integer with itself. This concept is fundamental in mathematics and helps in understanding various algebraic and geometric principles. A perfect square can be written in the form:
\[ n^2 \]
where \( n \) is an integer. For example:
- 1 is a perfect square because \( 1^2 = 1 \).
- 4 is a perfect square because \( 2^2 = 4 \).
- 9 is a perfect square because \( 3^2 = 9 \).
- 16 is a perfect square because \( 4^2 = 16 \).
To determine if a number is a perfect square, you can follow these steps:
- Find the square root of the number.
- Check if the square root is an integer.
- If the square root is an integer, then the number is a perfect square. If not, it is not a perfect square.
For instance, to check if 6 is a perfect square:
- Calculate the square root of 6, which is approximately 2.449.
- Since 2.449 is not an integer, 6 is not a perfect square.
Perfect squares have various applications in mathematics, including solving quadratic equations, understanding geometric shapes, and more. Recognizing and working with perfect squares is a valuable skill in both basic and advanced mathematical studies.
Mathematical Explanation
To understand why 6 is not a perfect square, we need to delve into the mathematical properties and calculations involved. A perfect square is defined as a number that can be expressed as the square of an integer. This means:
\[ n^2 = k \]
where \( n \) is an integer and \( k \) is the perfect square. For a number to be a perfect square, its square root must also be an integer. Let's apply this concept to the number 6.
- First, we calculate the square root of 6:
\[ \sqrt{6} \approx 2.449 \]
- Next, we check if the square root is an integer. In this case, 2.449 is not an integer.
- Since the square root of 6 is not an integer, 6 cannot be expressed as the square of any integer.
This shows that 6 is not a perfect square. For better understanding, let's compare 6 with some known perfect squares:
- \( 4 = 2^2 \), where the square root of 4 is 2, an integer.
- \( 9 = 3^2 \), where the square root of 9 is 3, an integer.
- \( 16 = 4^2 \), where the square root of 16 is 4, an integer.
In contrast, for 6:
\[ \sqrt{6} \approx 2.449 \]
Since 2.449 is not an integer, 6 does not qualify as a perfect square. This mathematical explanation highlights the fundamental property of perfect squares, emphasizing that only numbers with integer square roots can be considered perfect squares.
Calculating the Square Root of 6
To determine if 6 is a perfect square, we need to calculate its square root and verify if the result is an integer. Here is a step-by-step explanation:
- Understand the Concept:
The square root of a number \( k \) is a value that, when multiplied by itself, equals \( k \). In mathematical terms:
\[ \sqrt{k} = n \]
where \( n \times n = k \).
- Calculate the Square Root:
To find the square root of 6, we can use a calculator or perform a numerical approximation. Using a calculator, we get:
\[ \sqrt{6} \approx 2.449 \]
- Verify if the Result is an Integer:
Next, we check if 2.449 is an integer. Since it is not an integer, we can conclude that 6 is not a perfect square.
For further clarification, let's compare this with perfect squares:
- \( \sqrt{4} = 2 \), which is an integer, so 4 is a perfect square.
- \( \sqrt{9} = 3 \), which is an integer, so 9 is a perfect square.
- \( \sqrt{16} = 4 \), which is an integer, so 16 is a perfect square.
In contrast, for 6:
\[ \sqrt{6} \approx 2.449 \]
Since 2.449 is not an integer, 6 does not meet the criteria for being a perfect square.
This method of calculating and verifying the square root ensures that we accurately determine whether a number is a perfect square. In the case of 6, it is clear that it is not a perfect square due to its non-integer square root.
Properties of Perfect Squares
Perfect squares are unique numbers with distinct properties that distinguish them from other integers. Understanding these properties helps in recognizing and working with perfect squares in various mathematical contexts. Here are some key properties:
- Integer Square Roots:
A perfect square has an integer as its square root. For example, \( \sqrt{16} = 4 \), where 16 is a perfect square because 4 is an integer.
- Non-negative Values:
Perfect squares are always non-negative because they are the product of an integer with itself. This means:
\[ n^2 \geq 0 \]
for any integer \( n \).
- Sum of Odd Numbers:
Perfect squares can be represented as the sum of consecutive odd numbers. For example:
- \( 1 = 1 \)
- \( 4 = 1 + 3 \)
- \( 9 = 1 + 3 + 5 \)
- \( 16 = 1 + 3 + 5 + 7 \)
- Parity:
Perfect squares of even numbers are even, and perfect squares of odd numbers are odd. For example:
- \( (2k)^2 = 4k^2 \), which is even.
- \( (2k+1)^2 = 4k^2 + 4k + 1 \), which is odd.
- Ending Digits:
In decimal representation, perfect squares end in specific digits. The possible ending digits are 0, 1, 4, 5, 6, and 9. For example:
- 4 ends in 4 (i.e., \( 2^2 = 4 \)).
- 9 ends in 9 (i.e., \( 3^2 = 9 \)).
- 25 ends in 5 (i.e., \( 5^2 = 25 \)).
- Divisibility:
If a number is a perfect square, then its prime factors will all have even exponents. For example:
\( 36 = 2^2 \times 3^2 \)
Both 2 and 3 have even exponents.
These properties make perfect squares an integral part of number theory and various mathematical operations. Recognizing these properties helps in solving problems and understanding the behavior of numbers in different scenarios.
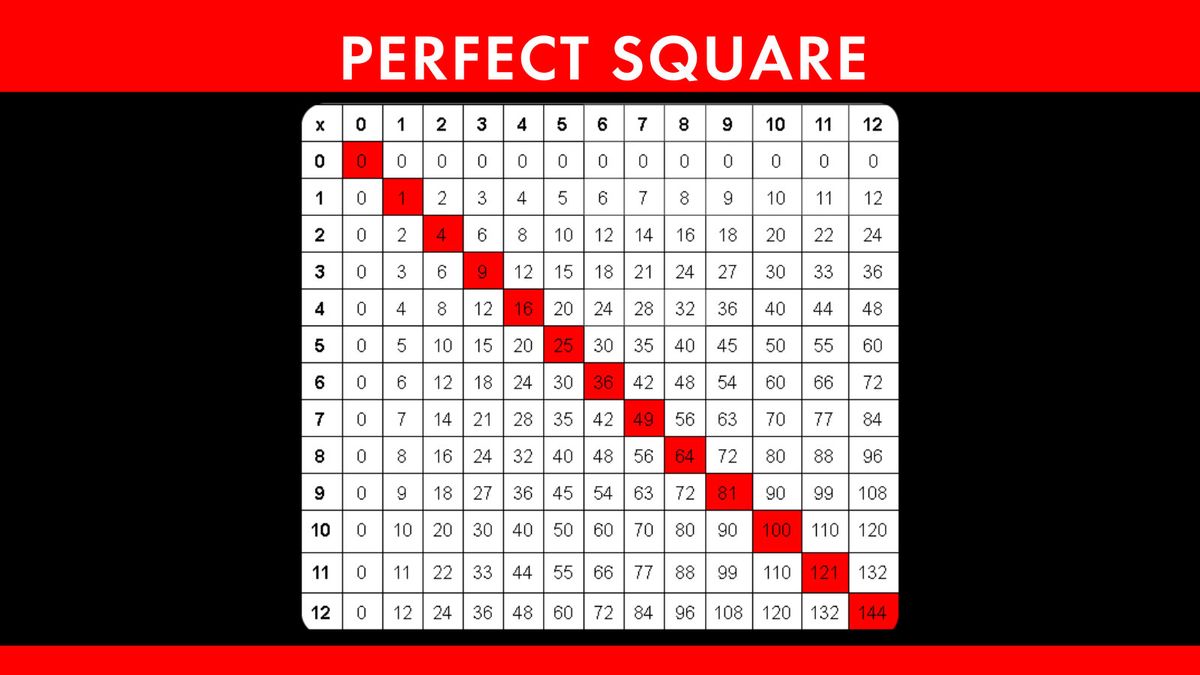
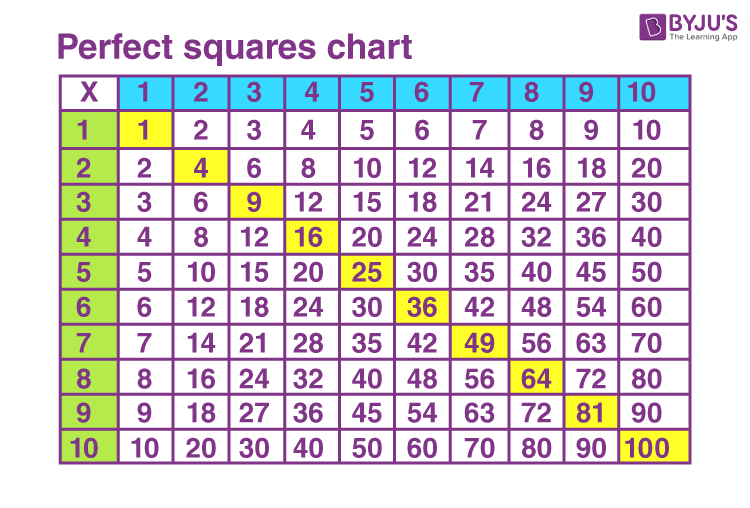
Examples of Perfect Squares
Perfect squares are numbers that can be expressed as the product of an integer with itself. These numbers are important in mathematics for various reasons, including their applications in algebra and geometry. Here are several examples of perfect squares:
- Small Perfect Squares:
- \( 1 = 1^2 \)
- \[ 4 = 2^2 \]
- \[ 9 = 3^2 \]
- \[ 16 = 4^2 \]
- \[ 25 = 5^2 \]
- Medium Perfect Squares:
- \[ 36 = 6^2 \]
- \[ 49 = 7^2 \]
- \[ 64 = 8^2 \]
- \[ 81 = 9^2 \]
- \[ 100 = 10^2 \]
- Larger Perfect Squares:
- \[ 121 = 11^2 \]
- \[ 144 = 12^2 \]
- \[ 169 = 13^2 \]
- \[ 196 = 14^2 \]
- \[ 225 = 15^2 \]
- Very Large Perfect Squares:
- \[ 400 = 20^2 \]
- \[ 625 = 25^2 \]
- \[ 900 = 30^2 \]
- \[ 1600 = 40^2 \]
- \[ 2500 = 50^2 \]
These examples illustrate the concept of perfect squares across a range of values. Each perfect square results from squaring an integer, producing a number with unique properties and applications in mathematical problems and real-world scenarios. By understanding and recognizing perfect squares, one can simplify calculations and solve equations more effectively.
Why 6 is Not a Perfect Square
To understand why 6 is not a perfect square, we need to review the definition of a perfect square and perform some mathematical calculations. A perfect square is a number that can be expressed as the product of an integer with itself. In other words, if \( n \) is an integer, then \( n^2 \) is a perfect square.
Let's explore this step by step:
-
Definition: A perfect square is a number that is the square of an integer. For example, 1, 4, 9, 16, and 25 are perfect squares because they can be written as \( 1^2 \), \( 2^2 \), \( 3^2 \), \( 4^2 \), and \( 5^2 \) respectively.
-
Square Root Calculation: To determine if 6 is a perfect square, we calculate its square root. The square root of 6 is approximately \( 2.449 \). Since this is not an integer, 6 cannot be written as the square of an integer.
Using Mathjax, this can be expressed as:
\[
\sqrt{6} \approx 2.449
\] -
Comparison with Perfect Squares: We can compare 6 to nearby perfect squares for further clarification:
- \( 2^2 = 4 \)
- \( 3^2 = 9 \)
Since 6 lies between 4 and 9 and is not equal to either, it is not a perfect square.
In summary, 6 is not a perfect square because its square root is not an integer. Perfect squares are the squares of whole numbers, and since \( \sqrt{6} \) is not a whole number, 6 does not meet the criteria for being a perfect square.
Misconceptions About Perfect Squares
Perfect squares are often misunderstood in various ways. Here, we will address some common misconceptions about perfect squares to clarify their properties and significance.
-
Misconception 1: Any number with an even number of factors is a perfect square.
This is incorrect. While perfect squares do have an odd number of factors, not all numbers with an even number of factors are perfect squares. For instance, the number 12 has six factors (1, 2, 3, 4, 6, 12), but it is not a perfect square.
-
Misconception 2: All even numbers are perfect squares.
This is a common misunderstanding. Perfect squares can be either even or odd. For example, 4 (even) and 9 (odd) are both perfect squares. The crucial criterion is that the number must be the square of an integer, not its parity.
-
Misconception 3: Numbers with non-integer square roots are close to being perfect squares.
Numbers with non-integer square roots are not perfect squares. For example, the square root of 6 is approximately 2.449, which is not an integer, indicating that 6 is not close to being a perfect square. Perfect squares have exact integer square roots, such as \(\sqrt{4} = 2\) and \(\sqrt{9} = 3\).
Using Mathjax, this can be expressed as:
\[
\sqrt{6} \approx 2.449
\] -
Misconception 4: A number's factors must always include pairs of identical factors for it to be a perfect square.
While it is true that perfect squares have pairs of identical factors, it is important to note that these factors must be integers. For example, 36 is a perfect square because it has factor pairs (1, 36), (2, 18), (3, 12), and (6, 6). The pair (6, 6) confirms it is a perfect square since \(6^2 = 36\).
-
Misconception 5: Perfect squares can only be formed from the product of small integers.
This is not true. Perfect squares can be formed from the product of any integer, regardless of size. For instance, \(100^2 = 10,000\) is a perfect square, as is \(1,000^2 = 1,000,000\).
Understanding these misconceptions helps clarify the true nature of perfect squares and avoids confusion when studying their properties and applications.
Real-World Applications
Perfect squares and their properties have numerous practical applications across various fields. Here are some of the ways they are utilized in the real world:
- Construction and Architecture:
In building construction, squaring is used to ensure that structures are built with precise measurements. For example, builders use squares to check that corners are perpendicular, which is crucial for the structural integrity of buildings. Square roots help in calculating the length of diagonal braces needed for stability.
- Finance:
In finance, square roots are used to calculate stock market volatility. This involves taking the square root of the variance of a stock's returns, helping investors assess the risk associated with particular investments.
- Science:
Square roots are essential in scientific calculations, such as determining the velocity of objects, the intensity of sound waves, and the absorption of radiation by materials. These calculations aid in understanding natural phenomena and developing new technologies.
- Statistics:
In statistics, squares and square roots are used to calculate variance and standard deviation, which measure how data points deviate from the mean. These metrics are vital for data analysis and interpretation.
- Geometry:
Geometry extensively uses squares and square roots for computing areas, perimeters, and solving problems involving right triangles. The Pythagorean theorem, for example, relies on these concepts to determine the lengths of sides in right-angled triangles.
- Computer Science:
In computer science, squares and square roots are used in algorithms for encryption, image processing, and game physics. Encryption algorithms use these concepts to secure data, while game physics relies on them for realistic motion and collision detection.
- Navigation:
Square roots are used in navigation to compute distances between points on maps or globes and to estimate bearings or directions. Pilots, for example, use these calculations to determine flight paths.
- Electrical Engineering:
Electrical engineering employs square roots to calculate power, voltage, and current in circuits. These calculations are critical for designing and analyzing electrical systems and devices.
- Cooking:
In cooking, scaling recipes often requires the use of square roots to adjust ingredient quantities proportionally. This ensures that the balance of flavors is maintained even when making larger batches.
- Photography:
The aperture of a camera lens, which controls light entry, is proportional to the square of the f-number. Adjusting the f-number changes the light entry significantly, affecting exposure and depth of field.
Understanding the concept of perfect squares and square roots can provide significant advantages in these diverse applications, highlighting their importance in both everyday tasks and advanced technical fields.
Khám phá căn bậc hai của các số chính phương cùng Thầy J. Video này giúp bạn hiểu rõ hơn về khái niệm số chính phương và cách tính căn bậc hai.
Căn Bậc Hai của Số Chính Phương | Toán học với Thầy J
READ MORE:
Khám phá căn bậc hai và số chính phương qua video này. Tìm hiểu cách nhận biết và tính toán căn bậc hai của các số chính phương.
Căn Bậc Hai Là Gì và Số Chính Phương Là Gì?